布里渊双波长窄线宽光纤激光器及其扫频微波信号生成

毕文文，冯 亭*，苏 鲸，延凤平，姚晓天

（1.河北大学物理科学与技术学院光信息技术创新中心，河北 保定 071002；2.河北省光学感知技术创新中心，河北 保定 071002；3.北京交通大学电子信息工程学院，北京 100044）

1 引 言

双波长单纵模（SLM）光纤激光器在光纤传感、密集波分复用、电子对抗、光纤通信、激光雷达探测、微波以及THz波信号生成等领域具有广泛的应用前景和巨大的应用潜力[1-7]。目前实现双波长SLM光纤激光器的方法主要有光纤光栅（FBG）超窄带滤波器[8]、可饱和吸收体[9]以及复合腔法[10]等，但以上在实现双波长激光输出时，具有成本高、损耗大、结构复杂等缺点。非线性频移也是一种有效的双波长激光实现方法[11-14]。自从1976年Hill等[15]首次报道了基于受激布里渊散射（SBS）的光纤激光器以来，由于其较低的相位噪声[16]、优异的相干性[17]和多波长稳定输出[18]等性能，被广泛研究。基于SBS的双波长光纤激光器因其结构简单、相位噪声低、功率损耗小和窄线宽输出等优点[16]，不仅在光通信和光纤传感等技术领域中得到了广泛关注，而且作为光生微波信号的优质光源具有巨大应用潜力。

利用残余泵浦光和布里渊激光拍频是一种实现微波信号生成的简单方法，在此基础上实现微波信号调谐可以采用以下措施：一是通过对SBS增益光纤施加应变以改变布里渊增益谱的位置，从而实现微波信号的调谐[12]；二是通过改变SBS谐振腔的温度实现微波信号的调谐[14]，但受限于温度的变化速度，微波信号调谐速度较慢；三是大范围调节泵浦光波长，可以在一定范围内改变SBS频移，从而实现微波信号调谐[19-20]，但该方法很受限于泵浦激光器的波长调谐特性。2017年，本课题组[21]采用1 km的单模光纤（SMF）作为SBS增益光纤，研制了双波长光纤激光器。在泵浦激光波长调谐范围宽达130 nm时，仅实现了拍频所得微波信号在894 MHz范围内的可调谐；而且由于激光器腔长很长，未能实现布里渊激光的SLM运行。

本文提出一种新型布里渊双波长光纤激光器，仅使用长度为3.0 m的高非线性光纤（HNLF）作为SBS增益介质，在6.6 m的谐振腔内实现了布里渊激光的SLM窄线宽运行。通过与残余泵浦光结合得到了稳定的高信噪比（OSNR）双波长激光输出，且经过拍频得到了频率为9.42 GHz的微波信号输出，又结合步进电机光纤拉伸机构对HNLF引入应变调制，获得了289.7 MHz范围的扫频微波信号。文中对布里渊激光的SLM、跳模、线宽等进行了详细的实验研究，同时对双波长拍频得到微波信号的扫频原理和步进电机拉伸HNLF应变调制实现微波信号的扫频特性进行了详细分析与讨论。

2 实验装置及原理

2.1 激光器实验结构及原理分析

图1为设计搭建的布里渊双波长光纤激光器结构图。窄线宽SLM光纤激光器（NKT Photonics，Koheras BASIK E15）作为泵浦激光种子源，使用高功率掺铒光纤放大器（EDFA，Connet，VLFS-1567-B-5000-FA）对其进行功率放大。使用环形器1（CIR-1）引入对应波长的FBG，将放大后的激光进行自发辐射（ASE）噪声的滤除，以增大泵浦激光信噪比。泵浦光经环形器2（CIR-2）进入布里渊激光谐振腔，对缠绕在光纤拉伸机构（Fiber stretcher）上的HNLF进行泵浦产生后向SBS。其中，HNLF（NL1550-Zero）在1 550 nm处的非线性系数为10 W-1·km-1、纤芯直径为3.79 μm。耦合器1（OC-1）将70%光保留到谐振腔内，耦合器2（OC-2）耦合比为50∶50。当入射光功率达到长度为3.0 m的HNLF的布里渊增益阈值时，能够激发一阶Stokes光，其反向传输经过CIR-2和OC-1，并在激光谐振腔内进行振荡，产生布里渊激光。布里渊激光与残余泵浦光在OC-2混合后共同输出，得到双波长激光输出。图1中蓝色线表示SMF，绿色线表示HNLF。

图1 布里渊双波长光纤激光器结构示意图Fig.1 Schematic of Brillouin dual-wavelength fiber laser

实现布里渊激光SLM输出的关键是激光谐振腔长和布里渊增益谱宽之间的匹配。考虑到所使用的HNLF与SMF的布里渊谱特性不同，搭建了光外差系统并对SBS增益谱随入纤泵浦光功率的变化规律进行了测量。图2为光外差系统示意图[22-23]，使用E15窄线宽激光器作为光源输入，经耦合器3（OC-3）分成两路，其中90%的光经过高功率EDFA后由CIR-1的2端口进入3.0 m的HNLF，反向传输的SBS经过CIR-1的3端口后由另一台EDFA（EDFA-1）放大，再与OC-3的10%端口输出的参考光在耦合器（OC-4）处混合。两信号拍频后由带宽为18 GHz的光电探测器（PD）检测并转化为电信号，再经电压放大器（Amp.）放大后进入射频（Radio frequency，RF）频谱分析仪（ESA，Keysight N9010A）进行测量。图2中黑色线表示电信号传输线。

图2 外差法测试布里渊增益谱系统示意图Fig.2 Schematic of heterodyne method for measuring Brillouin gain spectrum

在不同入纤泵浦光功率下测量布里渊增益谱，使用ESA的平均模式测量100次，测量范围为300 MHz，测量分辨率带宽（Resolution bandwidth，RBW）为100 kHz，如图3所示。HNLF的入纤泵浦光功率通过激光功率计在CIR-1的2端口处直接测量。可以看出，布里渊增益谱呈洛伦兹线型，且随着入纤泵浦光功率的不断增加，布里渊增益峰值功率也随之变大。分别对不同功率下布里渊增益谱的谱宽进行洛伦兹拟合并计算布里渊增益谱的3 dB带宽，得到布里渊增益谱宽随入纤泵浦光功率的变化规律，如图4所示。可以看出，当入纤泵浦光功率较低时，布里渊增益谱较宽，但随着入纤泵浦光功率的增加，布里渊增益谱宽随之降低，与SMF的布里渊增益谱变化规律比较一致[24]。

图3 3.0 m长HNLF布里渊增益谱随入纤泵浦光功率的变化Fig.3 Brillouin gain spectrum of HNLF with 3.0 m length varies with the input pump laser power

图4 3.0 m长HNLF布里渊增益谱宽随着入纤泵浦光功率的变化Fig.4 Brillouin gain spectrum width variation of 3.0 m long HNLF versus input pump laser power

由于存在器件发热引起的性能漂移现象，激光器工作时不宜采用太高的泵浦光功率，本文工作主要以高功率EDFA输出功率3 W为代表开展研究。经测量得知，图1中从高功率EDFA输出到进入HNLF之前的泵浦激光功率总损耗为2.3 dB，即当高功率EDFA输出激光功率为3.0 W时，HNLF的入纤泵浦光功率约为1.8 W，此时对应的图4中布里渊增益谱宽约为26 MHz。测量可知布里渊激光谐振腔长为6.6 m，对应的纵模间隔约为31 MHz，已大于此时的布里渊增益谱宽，因此理论上能够保证布里渊激光的单纵模运行。

2.2 光纤应变调制方法

作为非线性散射效应中的一种，SBS是由石英光纤中声子引起的，布里渊频移量取决于光纤的声学和热学等特性。当光纤温度变化或产生应变时，纤芯有效折射率和光纤中声速会随之改变，导致光纤的布里渊频移发生改变[25]。对于普通石英SMF，在波长λp=1 550 nm、温度T0=20℃时，布里渊频移νB和应变量ε之间的关系可以表示为[26]:

可以计算得出布里渊频移量与应变量之间成正比例关系，比例系数为0.048 MHz/με。对增益光纤引入应变可以实现双波长激光拍频微波信号调谐，假设HNLF具有类似于SMF的比例系数，则对3.0 m长HNLF每引入500 με，理论上布里渊激光能够实现～24.0 MHz的频移，即微波信号能在9.42 GHz附近实现～24.0 MHz的频率变化。

定制了步进电机光纤拉伸机构以实现光纤应变调节，如图5所示，步进电机具有推力大、位移量大且位移形式灵活等优点。光纤绕接形状为跑道型，绕接体分为左侧半圆柱体和右侧半圆柱体，半径均为5 cm，且左侧半圆柱体固定，右侧半圆柱体做往返运动。半圆柱体外侧刻有直径为250 μm的凹槽以便固定光纤，防止光纤在拉伸过程中上下滑动损失位移，凹槽表面做硬化及光滑处理来减小光纤与半圆柱体之间的摩擦。步进电机螺杆单圈旋转轴向走程为2.54 mm，每圈旋转可由3 200个脉冲驱动步进，电机长度为15 cm，最小推力为3 500 N。

图5 步进电机光纤拉伸机构实物图Fig.5 Photo of fiber stretcher based on step motor

3 结果与讨论

3.1 激光输出性能测量

图6（a）所示为滤除高功率EDFA输出的ASE所使用的FBG的反射光谱，由光谱仪（OSA，Yokogawa AQ6370D）测量的光谱数据经反射率归一化处理后得到。测量时，OSA分辨率设置为0.02 nm，数据采样间隔为0.001 nm。由图6（a）可见，FBG的中心波长为1 550.155 nm，带宽为0.17 nm，反射率为81.67%。图6（b）中红色实线所示为FBG滤除高功率EDFA的ASE后的双波长激光输出光谱，激光波长分别为1550.166 nm和1 550.242 nm，OSNR＞77 dB，与 未 经FBG滤 除ASE的双波长激光输出（蓝色虚线）相比，OSNR提高了28 dB。然后，断开图1中的a点后测量光谱，如图6（c）所示，可见只有布里渊激光输出，其波长为1 550.242 nm，OSNR＞77 dB。

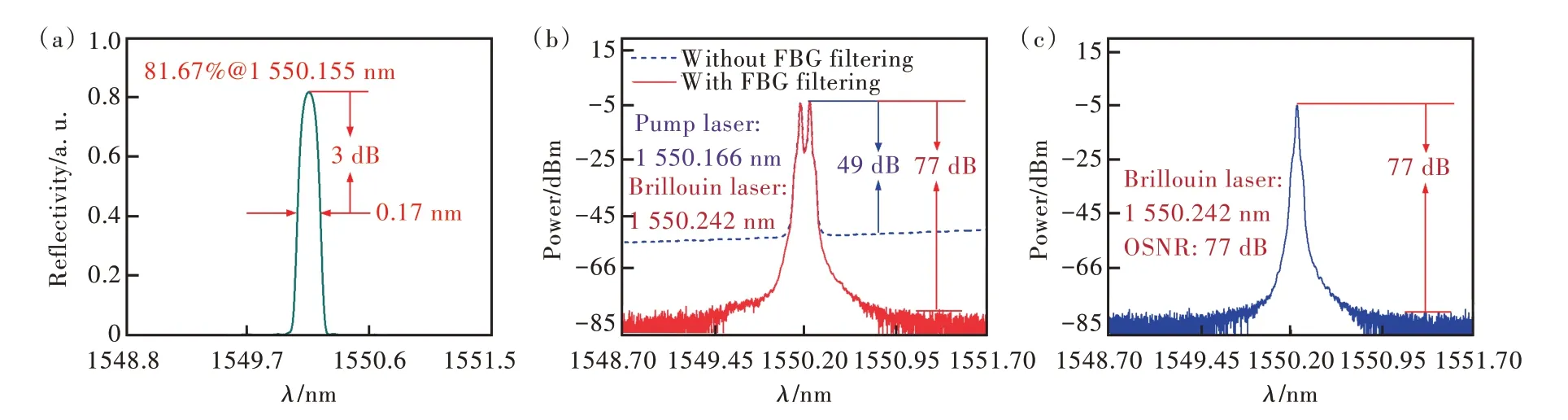
图6 （a）FBG反射光谱；（b）有、无FBG滤波的双波长激光输出光谱；（c）布里渊激光输出光谱。Fig.6（a）Reflection spectrum of FBG.（b）Dual-wavelength laser output spectra with and without FBG filtering，respectively.（c）Brillouin laser output spectrum.

图7（a）为使用自零差法测试激光SLM运行的实验结果，使用ESA的最大值保持模式进行扫描测量，测量时间为30 s，RBW为51 kHz。可以看出，在0～400 MHz扫描范围内无明显的拍频信号，考虑到主腔纵模间隔约为31 MHz，可以认为激光器运行在SLM状态。图7（b）为利用延迟自外差法测量布里渊激光的跳模特性，测量系统由带宽400 MHz的光电探测器（PD）、两臂分别加入200 MHz的声光调制器（AOM）和100 km长SMF延迟线的马赫-曾德尔光纤干涉仪、ESA组成。使用ESA的最大值保持模式测量，RBW设置为51 kHz。其中，插图给出的是测量范围为175～225 MHz、RBW为30 kHz的测量 结果。可以看出，只有AOM引入的200 MHz的强拍频信号被捕捉到，在100次重复测量和最大值保持模式下并没有观察到其他明显的拍频信号，意味着SLM布里渊激光在长时间运行下未发生模式跳变。同时，利用延时自外差法对泵浦激光和布里渊激光的线宽进行 测 量，ESA测 量 范 围 为100 kHz、RBW设 置 为100 Hz。图8（a）、（b）中分别给出了泵浦激光和布里渊激光的实验测量数据及洛伦兹拟合曲线，拟合优度分别为0.899 50和0.900 01。图中给出了拟合曲线20 dB带宽分别为18.31 kHz和12.45 kHz，计算两数值的1/20倍分别得到泵浦激光和布里渊激光的线宽为915.50 Hz和622.50 Hz。可见，布里渊激光对泵浦激光的线宽具有明显的压窄效果。

图7 （a）自零差法测量的布里渊激光SLM运行结果；（b）延时自外差法测量的SLM布里渊激光无跳模运行结果。Fig.7（a）Measurement of SLM Brillouin lasing，using selfhomodyne method.（b）Measurement of mode-hoppingfree SLM Brillouin lasing，using delayed self-heterodyne method.

图8 （a）泵浦激光线宽测量；（b）布里渊激光线宽测量。Fig.8（a）Linewidth measurement of pump laser.（b）Linewidth measurement of Brillouin laser.

图9给出了布里渊激光输出功率与HNLF入纤泵浦激光功率的关系，蓝色点为实际测量数据，红色线为对实验数据线形区域的直线拟合，拟合优度为0.993 65。从图中可以看出，随着入纤泵浦光功率的不断增加，布里渊激光由0 mW不断增加至85.1 mW；但在入纤泵浦光功率小于955.6 mW时，随着入纤泵浦光功率的增加，输出光功率没有明显增加；而在955.6 mW之后，随着入纤泵浦光功率的增加，输出光功率近似于线性增加，且在泵浦光功率达到1.5 W之后，斜率开始降低，布里渊增益逐渐达到饱和。由以上分析可以认为，激光器的布里渊激光阈值为955.6 mW。另外，由线性拟合可得到布里渊激光输出的斜率效率仅为14%，主要是因为腔内损耗较大、HNLF的非线性系数较小，可以通过优化腔损和使用更高非线性系数的HNLF进一步提高。

图9 布里渊激光输出功率与HNLF泵浦激光功率的关系Fig.9 Brillouin laser output power versus pump laser power of HNLF

3.2 微波信号扫频性能测量

使用带宽为18 GHz、阈值为10 mW的PD通过自零差法拍频双波长激光输出得到微波信号，由ESA测量结果如图10所示。可以看出，在26 GHz范围内只有9.4 GHz附近有一微波信号，且从插图可见该微波信号频谱纯净。由2.2节分析可知，HNLF的布里渊增益谱会随着其应变的变化而移动，将3.0 m长HNLF缠绕于步进电机光纤拉伸机构上并通过拉伸引入应变，理论上光纤拉伸机构每拉伸1.5 mm对应HNLF产生500 με。在入纤泵浦光功率为1.8 W时，测试了拉伸机构对于双波长激光拍频所得微波信号频率的调谐能力，如图11所示。表1中给出了不同应变量下对应的微波信号频率。可以得出，HNLF的应变量从0 με以500 με为间隔增加到6 000 με时，微波信号频率总计变化了305.5 MHz，且微波信号频率依次增量为27.6，26.7，23.9，24.2，29.0，19.9，27.7，25.2，27.1，24.6，25.1，24.5 MHz，平均增量为25.4 MHz，与2.2节理论计算的24.0 MHz接近。

图10 双波长光纤激光输出拍频产生的微波信号Fig.10 Microwave signal generated by frequency beating of the dual-wavelength fiber laser output

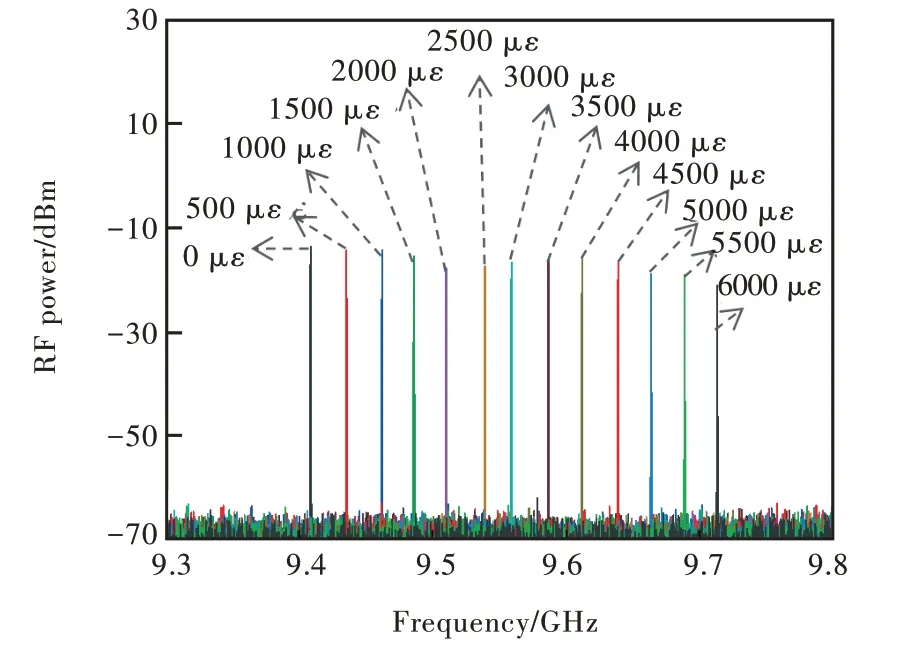
图11 HNLF受不同应变时测量的微波信号Fig.11 Microwave signals measured when HNLF is under different strains

表1 HNLF受不同应变时测量的微波信号的频率Tab.1 Microwave signal frequencies measured when HNLF is under different strains

为了验证微波信号的频率扫描特性，设置步进电机光纤拉伸机构为扫描模式，扫描频率为10 Hz，从HNLF施加0～2 000 με开始，以400 με为间隔增加扫描范围，最大到0～6 000 με，对微波信号的频率扫描特性分别进行测量。设置ESA为最大保持测量模式，并在30 s内对扫频微波信号进行测量，实验结果如图12（a）所示。可以看出，随着应变调谐范围的增加，微波信号扫频范围不断增加。取最大值保持模式测量扫描光谱的20 dB宽度为微波信号扫频范围，由图12（a）可得HNLF应变量与微波信号扫频范围的关系，如图12（b）所示，且对实验数据进行线性拟合，拟合优度达到0.998 52，说明具有良好的线性变化关系。值得注意的是，在应变调制范围为0～6 000 με时，微波信号扫频范围为289.7 MHz，小于图11中测得的在固定应变量为6 000 με时微波信号频率变化量305.5 MHz，说明在扫描模式下，步进电机光纤拉伸机构对HNLF施加的光纤拉伸量有一定量的损失，从而导致微波信号扫频范围缩小。另外，图12（b）中拟合直线的斜率为0.048 MHz/με，与2.2节理论得到的SMF的布里渊频移量与应变量比例系数一致[25]。此外，在不超出HNLF弹性限度范围内，可以通过增加应变调制范围进一步增加微波信号的扫频范围。

图12 （a）HNLF不同应变扫描调制范围对应的微波信号扫频测量；（b）微波信号扫频范围与HNLF应变调谐范围的关系。Fig.12（a）Spectra of frequency-swept microwave signals under different strain-swept range of HNLF.（b）Frequency-swept range of microwave signal versus strainswept range of HNLF.

由于使用步进电机进行光纤应变调制，其基于脉冲信号驱动螺杆转动而实现轴向位移，单圈由3 200个脉冲驱动电机螺杆轴向运动2.54 mm，即步长为0.79 μm，对应缠绕的HNLF的应变量2.57 με，再由实验得到的布里渊频移应变调制系数0.048 MHz/με可得微波信号扫频调谐频率分辨率为123.36 kHz。

4 结 论

本文提出了一种基于HNLF的布里渊光纤激光器，谐振腔长为6.6 m，纵模间隔约为31 MHz，有效保证了在布里渊增益谱内实现激光SLM运行，得到了线宽仅为622.50 Hz的布里渊激光输出。结合残余泵浦光，实现了稳定的高信噪比（＞77 dB）双波长窄线宽激光同时输出，通过拍频得到了频率在9.4 GHz的窄线宽微波信号。设计定制了基于步进电机的光纤拉伸机构对HNLF进行扫描应变调制，在10 Hz扫描频率下得到了289.7 MHz范围的微波信号扫频运行，频率分辨率为123.36 kHz。提出的双波长光纤激光器及作为扫频微波源在光/无线通信、光纤传感、微波光子学等领域具有潜在的应用价值。

本文专家审稿意见及作者回复内容的下载地址：http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20220176.