基于PLS子空间对齐的2,6-二甲酚纯度迁移学习建模
邬云飞,栾小丽,刘 飞
江南大学自动化研究所,轻工过程先进控制教育部重点实验室,江苏 无锡 214122
引 言
物质浓度在线测量是产品质量控制的关键,主要通过测量样品体系中随物质浓度改变而变化的物理化学性质关联得到[1]。近红外光谱是一种先进的在线过程检测技术,其原理是使用13 333~4 000 cm-1波长范围的电磁辐射探测样品获得光谱信息[2],通过化学计量学方法建立光谱信息与物质浓度之间的关系,已被广泛用于化工[3-4]、 制药[5]、 生物[6]、 食品[7]和医疗[8]等行业。近红外光谱检测结果的准确性与模型的质量密切相关,研究人员已经提出了很多方法来构建校正模型,比如偏最小二乘回归、 多元线性回归、 主成分回归等。随着机器学习技术的发展,Chen等[9]提出了一种用于建立光谱校正模型的贝叶斯方法,建立的贝叶斯模型具有较低的预测误差;Bian等[10]引入极限学习机算法用于复杂样品的光谱定量分析,兼顾了模型的预测精度和稳定性;Yang等[11]将深度学习用于光谱分析,提高了对数据集的特征提取能力,但是对样本量的需求较大。
在使用近红外光谱进行在线测量时,需要足够多的历史样本离线构建模型。然而在实际工业生产过程的最后阶段,样品的纯度越来越高,样本的多样性不足,物质浓度与光谱之间缺乏相关性。在这样的数据条件下,传统方法建立的模型很难达到期望的预测性能。例如,在重要的化工中间体2,6-二甲酚(2,6-dimethylphenol,2,6-DMP)的生产过程中,由于产品塔的产品纯度较高,近红外检测数据缺乏多样性,模型的泛化能力较弱。针对高质量训练数据较少的问题,迁移学习能够从相关领域迁移信息来改进目标领域的模型性能,从而减少对目标领域数据数量和质量的依赖[12]。Liu等[13]采用迁移学习策略,扩展了样本的数量和多样性,提高了故障诊断结果的稳定性和准确性;Wang等[14]运用基于局部相似特征选择的迁移学习方法,对不同原油在不同检测条件下的近红外光谱数据实现了快速建模;褚菲等[15]将迁移学习方法与多尺度核学习方法相结合,改善了间歇过程产品质量的预测精度。
借鉴迁移学习中不同数据域的知识传递思想,本研究针对高纯度的产品塔2,6-DMP在线检测问题,利用其他塔的光谱数据和产品塔光谱数据的相似性,提出了一种基于偏最小二乘(PLS)子空间对齐的迁移学习建模方法。首先借助偏最小二乘为产品塔和其他塔的数据集创建子空间,然后学习其他塔到产品塔数据集子空间的映射函数,并将其他塔的样本数据投影到对齐之后的子空间以生成新的特征表示,最后采用迁移之后的新特征建立模型。基于子空间的迁移学习中,通常采取寻找公共子空间或者构建一组中间表示的策略,不仅可能代价高昂,还会造成源域和目标域信息的损失。通过PLS子空间对齐可以直接比较各数据域的样本特征,无需进行其他的投影。该方法可以充分利用其他塔多样性较好的光谱数据,为产品塔建立具有可靠性和高预测精度的模型,从而实现2,6-DMP产品质量的实时调控。
1 实验部分
1.1 偏最小二乘回归算法
在产品分离提纯过程中,混合体系由多组分构成,组分的种类和含量未知,不同种类物质的近红外光谱特征吸收峰存在重叠,不能对一系列标准溶液做出校正曲线。偏最小二乘(partial least squares,PLS)方法通过在特征空间内提取主成分来描述光谱数据与纯度值之间的关系,适用于样本数较少而变量数较多的过程建模,能够用于产品纯度的在线测量[1]。
光谱数据X={xi;i=1,…,n},与2,6-DMP纯度Y={yi;i=1,…,n},其中n是样本数目。PLS分别从X和Y中提取主成分t1和u1,它们必须满足:
(1)t1和u1应该分别携带尽可能多的X和Y的变异信息,即var(t1)→max,var(u1)→max;
(2)t1和u1之间的相关性最大,即r(t1,u1)→max。
上述两个条件综合起来,即要求t1和u1的协方差达到最大
(1)
式(1)中,cov(·,·)表示协方差,var(·)表示方差,r(·,·)表示相关系数。式(1)可转化成下列优化问题
(2)
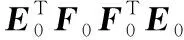
提取第一个主成分后,建立E0,F0对t1的回归模型,然后运用E0,F0被t1解释后的残差信息提取第二个主成分t2,重复该过程,直到提取A个主成分满足精度要求。PLS算法提取主成分过程如下(i=1∶A):
(1) 通过特征值分解法获得wi和ci;
(2) 计算主成分ti,载荷向量pi,系数向量ri以及残差信息Ei和Fi:
ti=Ei-1wi
通过以上步骤,提取到主成分T=(t1, …,tA),获得载荷矩阵P=(p1, …,pA),系数矩阵R=(r1, …,rA)和W=(w1, …,wA)。
主成分与矩阵E0的关系为
T=E0V
(3)
式(3)中,V=W(PTW)-1表示投影矩阵。
最终可以得到模型回归系数,见式(4)
β=VRT
(4)
1.2 基于PLS的子空间对齐方法
子空间对齐(subspace alignment,SA)方法使用主成分分析(principal component analysis,PCA)为源域数据和目标域数据提取d个特征向量,作为源域和目标域子空间的基,用ZS和ZT表示。然后使用映射矩阵M∈Rd×d对齐两个域的基向量,将源域子空间坐标系转换为目标域子空间坐标系,矩阵M通过最小化布雷格曼矩阵散度(Bregman matrix divergence)获得,见式(5)
(5)

(6)
主成分回归进行降维时仅考虑光谱数据X,而在偏最小二乘回归中考虑了光谱数据X与纯度值Y之间的关系,不仅能概括光谱数据中所包含的信息,也能更好地解释纯度值。将子空间对齐方法拓展到偏最小二乘回归中,具体描述如下:
(1) 输入:其他塔的样本集(XS,YS),产品塔样本集(XT,YT),标准化处理后分别为(ES,FS)和(ET,FT)。
(2) 首先采用PLS算法分别获得其他塔和产品塔各自子空间的投影矩阵VS和VT;
(7)
式(7)中,“+”表示广义逆;
(4) 计算迁移后其他塔的投影矩阵Vtrans和主成分Ttrans,见式(8)
Ttrans=XSVtrans
(8)
(5) 计算迁移后其他塔的载荷矩阵Ptrans和系数矩阵Rtrans(i=1∶A)
ti=Ttrans(∶,i)
Ptrans(∶,i)=pi
Rtrans(∶,i)=ri
(6) 计算迁移后的回归系数,见式(9)
(9)
(7) 输出:采用竞争学习加权策略(winner-takes-all based weighting method)[16],即计算产品塔回归系数βt和迁移后其他塔回归系数βtrans对应的交叉验证均方根误差,选择误差较小的作为最终的模型回归系数βf,算法流程如图1所示。
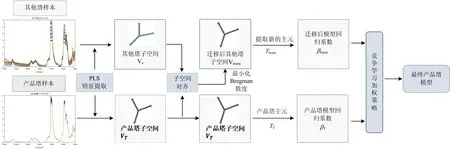
图1 迁移学习算法建模流程图Fig.1 Modeling flow diagram of transfer learning algorithm
2 结果与讨论
2.1 过程描述
目前国内外合成2,6-DMP的主要方法有天然分离法、 苯胺重氮化水解法、 甲苯氯化水解法及苯酚烷基化法。工业上常用苯酚烷基化法,该方法选择性较高且成本较低,适宜连续生产,本文研究的2,6-DMP制备过程如图2(a)所示。

图2 工艺流程与反应原理 (a):工艺流程图;(b):反应原理图Fig.2 Process flow diagrams and Reactive principle sketch (a):Process flow diagram;(b): Reactive principle sketch
以苯酚和甲醇为原料,选择合适的催化剂后在固定床管式反应器进行烷基化反应,反应原理如图2(b)所示。反应气依次经过脱醇水塔、 脱苯酚塔和邻甲酚粗品塔,到达2,6-DMP产品塔,在产品塔顶部获得产品2,6-DMP。由图2(b)可知,产物含有邻甲酚及其他杂质,为了在线检测生产流程中各组分的含量,分别在脱苯酚塔的底部、 邻甲酚粗品塔的底部和2,6-DMP产品塔的顶部安装了近红外光谱仪和检测探头,在线收集管道中物料的近红外光谱数据,通过已建立的模型得到产品纯度的预测值。
2,6-DMP产品塔的产品纯度高,化验室通过气相色谱法标注的纯度值分布在一个较小的区间内,且存在很高的重复性,传统的建模方法无法精确建模。在产品2,6-DMP的精馏提纯过程中,不同检测点处样品有机物的含量和种类不同,脱苯酚塔和邻甲酚粗品塔检测点采集的光谱数据与产品塔存在差异,但是样品中有机成分种类有重合,近红外光谱在相同波数处存在相似的的吸收峰,如图3所示。本工作提出的一种基于PLS子空间对齐的迁移学习建模方法能够利用这种相似性,借助其他检测点的光谱数据,有效提升产品塔检测点模型的性能。
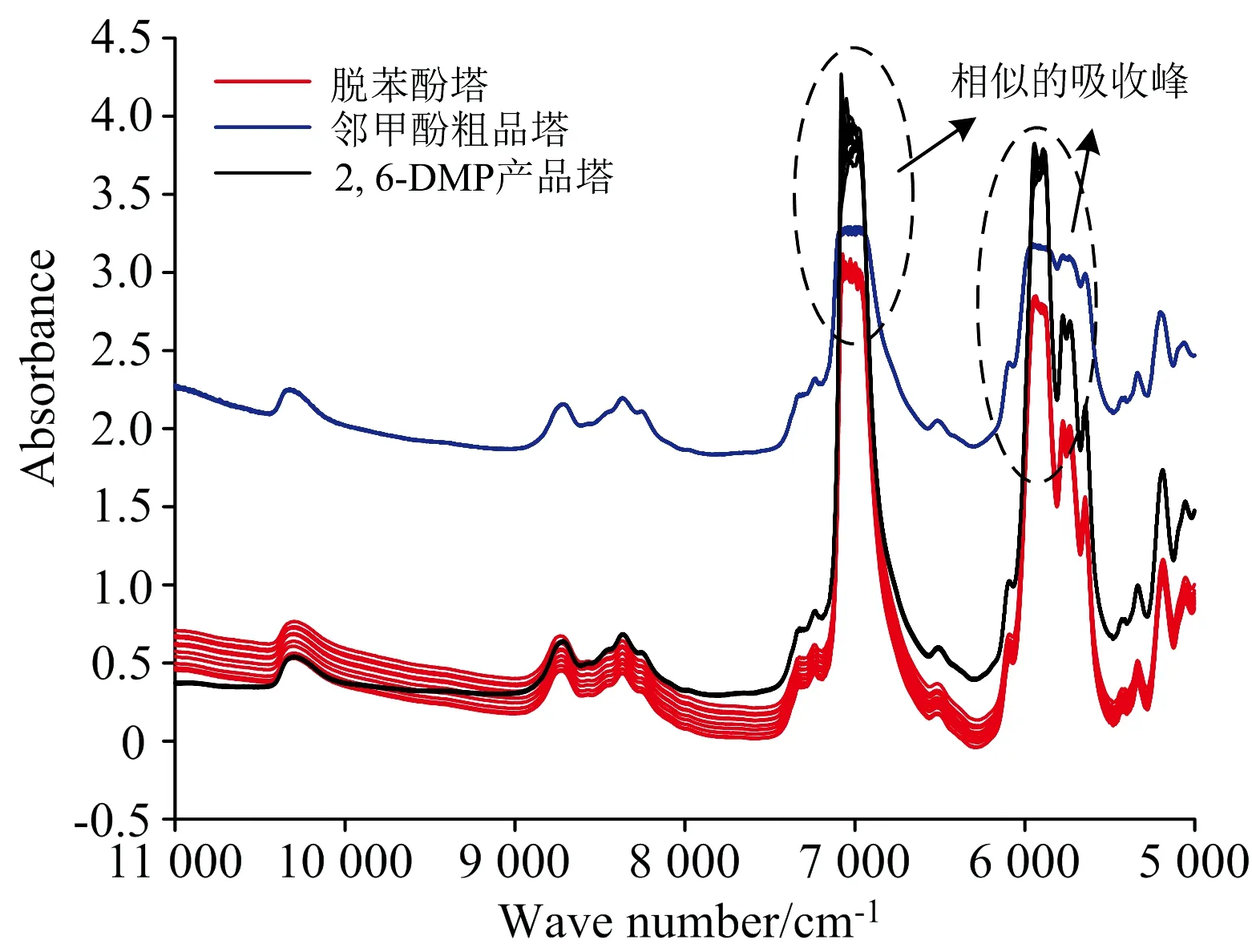
图3 不同检测点处的光谱比较Fig.3 Spectral comparison at different detecting points
2.2 数据
建模所用的原始光谱来自某合成材料公司的2,6-DMP制备过程。使用布鲁克在线近红外光谱仪采集样本光谱,扫描光谱范围为12 500~4 000 cm-1,实际使用范围11 000~5 000 cm-1。近红外光谱数据集对应的2,6-DMP纯度值由化验室通过气相色谱法分析离线获得,各个检测点的纯度值数据特征如表1所示。采用变异系数来衡量样本离散程度,因为标准差是一个绝对指标,当用其来对同一总体的不同时期进行对比时,由于平均值不同,缺乏可比性。变异系数是标准差与平均值的比值,可以消除平均值不同对样本集离散程度对比的影响。通过比较变异系数发现,产品塔的变异系数明显小于脱苯酚塔和邻甲酚粗品塔,说明产品塔的样本区分度低。
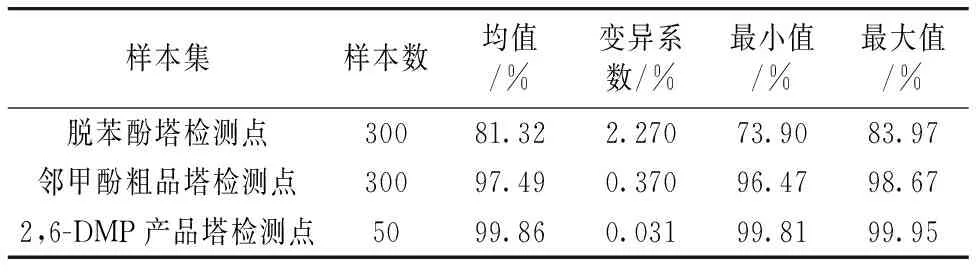
表1 不同检测点的2,6-DMP纯度值特征Table 1 2,6-DMP purity distribution at differentdetecting points
2.3 实验结果
(1)将2,6-DMP产品塔检测点获得的数据集中30组数据作为训练集,20组数据作为测试集。模型性能的评价指标采用近红外光谱分析方法中最常用的预测均方根误差(root mean square error of prediction,RMSEP)[2],计算公式如式(10)
(10)
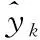
为了更直观地观察PLS子空间对齐方法的效果,引入指标性能提升百分比IP,计算公式如式(11)所示。
(11)
式(11)中,RMSEPPLS为仅使用产品塔训练集训练PLS模型的预测均方根误差,RMSEPPLS-SA为使用PLS子空间对齐方法训练模型的预测均方根误差。
(2)分析不同数量的辅助光谱对2,6-DMP产品塔模型性能的影响,将脱苯酚塔检测点和邻甲酚粗品塔检测点采集的光谱数据,按照不同数量(30~300)依次加入到产品塔训练集中。为了证明PLS子空间对齐方法的有效性,与传统机器学习方法支持向量机回归和BP神经网络进行了比较,支持向量机回归选择高斯核函数,脱苯酚塔样本作为辅助数据时核参数选择4.5,邻甲酚粗品塔样本作为辅助数据时核参数选择5.5;BP神经网络隐藏层神经元个数选择5,最大迭代次数为100。
PLS子空间对齐方法中唯一的参数是主成分数,选取与产品塔训练集同样数目的脱苯酚塔样本和邻甲酚粗品塔样本,比较不同主成分数下的模型性能,结果如图4所示。在主成分数较少时,模型的预测均方根误差较小,性能较高,最后选择因子数为7,此时仅使用产品塔训练集构建模型的预测均方根误差值为0.059 4。
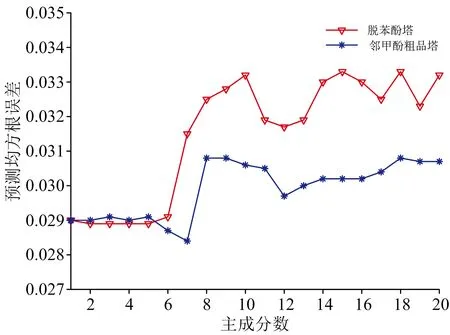
图4 不同主成分数对模型性能的影响Fig.4 Different principal component numbersimpact on model performance
图5(a)和图6(a)分别是迁移脱苯酚塔不同数量样本辅助建模所得的建模误差和迁移邻甲酚粗品塔不同数量样本辅助建模所得的建模误差,红色曲线表示运用PLS子空间对齐方法的建模误差,蓝色曲线表示其他塔样本与产品塔样本合并后运用PLS算法的建模误差,黑色曲线表示运用支持向量机回归算法的建模误差,绿色曲线表示使用BP神经网络算法的建模误差。图5(b)和图6(b)分别是迁移脱苯酚塔样本数据后的性能提升百分比和迁移邻甲酚粗品塔样本数据后的性能提升百分比。
从图5和图6中可以看出,相较于传统方法,PLS子空间对齐方法对产品塔的模型性能有明显的提升。随着样本数的增加,模型的性能提升呈下降趋势,且脱苯酚塔的样本作为辅助数据,在样本量超过240时,对模型性能已没有提升,表明随着辅助数据数量的增加,引入了对产品塔模型有害的样本,导致了负迁移。
观察图5和图6可知,借助邻甲酚粗品塔30个样本时,模型性能的提升最大,此时预测均方根误差为0.028 4,性能提升百分比为52.19%。图7(a)是此时的模型曲线,图7(b)是预测值与实际值的散点图。从图7可以看出,PLS子空间对齐方法建立的模型预测效果更好。
3 结 论
针对产品生产最后阶段物质浓度提高,样本区分度低,多样性不足,无法精确建模的问题,提出了一种基于PLS子空间对齐的迁移学习建模方法。在偏最小二乘回归算法的基础上,为两个域创建子空间,然后最小化布雷格曼矩阵散度从而获得源子空间到目标子空间的映射,完成源域特征到目标域特征的迁移。在某公司制备2,6-二甲酚过程的近红外检测数据集上进行了仿真验证,结果表明,所提方法能够借助其他塔的数据来提升产品塔高浓度产品检测模型的稳定性和准确性,具有一定的实用价值。在后续的工作中将进一步研究迁移模型性能与样本数量之间的定量关系以及如何避免负迁移。
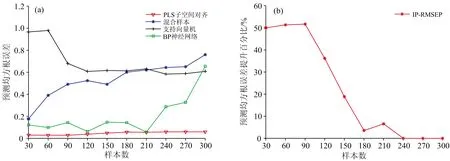
图5 迁移脱苯酚塔不同样本数对模型性能的影响 (a):迁移脱苯酚塔不同样本数对模型性能的影响;(b):迁移脱苯酚塔不同样本数的模型性能提升百分比Fig.5 Different sample numbers of dephenolization tower impact on model performance (a):Impact on model performance for transferring different sample numbers of dephenolization tower; (b): Model performance improvement percentage for transferring different sample numbers of dephenolization tower
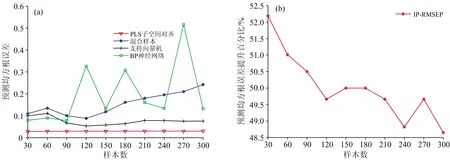
图6 迁移邻甲酚粗品塔不同样本数对模型性能的影响 (a):迁移邻甲酚粗品塔不同样本数对模型性能的影响;(b):迁移邻甲酚粗品塔不同样本数的模型性能提升百分比Fig.6 Different sample numbers of o-cresol tower impact on model performance (a):Impact on model performance for transferring different sample numbers of o-cresol tower; (b): Model performance improvement percentage for transferring different sample numbers of o-cresol tower

图7 模型曲线与散点图 (a)模型曲线;(b):预测值与实际值散点图Fig.7 Model curve and Scatter plot (a):Model curve;(b): Scatter plot of prediceted and actual values

