车载边缘计算中推理任务的实时调度策略
陈乔鑫,卢 宇,林 兵,3+,王素云,邵 浚
(1.福建师范大学 物理与能源学院,福建 福州 350117;2.福建师范大学 协和学院,福建 福州 350117;3.北京大学 信息科学技术学院,北京 100871)
0 引言
车联网作为5G场景下的关键应用场景,已经成为研究的热点领域,未来发展前景较好,其衍生的自动驾驶技术不但可以提高驾驶过程中的安全性,而且有利于解决城市中愈发严重的交通效率低下、车道拥塞等难题。然而,自动驾驶是计算密集型、时延敏感型的应用,其计算复杂度高且完成时延要求严格,仅由计算能力有限的车载终端执行通常无法满足要求[1]。之前自动驾驶的多数研究集中于将车辆驾驶过程中的交通状况识别等具体功能设计为推理任务[2-3],较少关心如何调度推理任务,不可避免地出现了高延迟。而在车联网环境下引入移动边缘计算(Mobile Edge Computing, MEC)能够将车载终端中的实时任务卸载到路边单元(Road Side Unit, RSU),从而有效缓解车辆终端算力低下、存储资源匮乏等困境,在边缘环境中合理调度推理任务则可有效降低任务的执行时间,满足低延迟约束[4-6]。由于不同场景下的任务结构不全相同,边缘节点也存在性能差异,设计合理的调度策略成为研究难题。
为此,国内外进行了大量研究。启发式算法广泛应用于任务调度问题与协同任务方面,基本原型如粒子群优化(Particle Swarm Optimization, PSO)算法、蚁群算法(Ant Colony Algorithm, ACA)、遗传算法(Genetic Algorithm, GA)等[7-9],这类方法可在约束条件下找到符合条件的可行解,但由于无法预计可行解与最优解之间的偏差,收敛速度较慢,在有限的决策时间中往往只能求得局部最优解,这类解较难满足低时延任务的要求。因此近年来,部分研究者利用强化学习思想解决边缘卸载问题,通过不断矫正可行解与更优解的偏差,在加快收敛速度的同时增强探索力。LIN等[10]分别采用PSO算法和Q学习算法对车联网的实时任务进行策略调度,具有指导意义,然而任务模型较理想化,未考虑任务优先级,忽略了应用中任务执行顺序不同对完成时间的影响;赵海涛等[11]针对车联网环境下不同车辆的任务提出优先级概念,令任务分配更加合理,然而所提优先级划分方法倾向于专家评定,过于主观;XIONG等[12]和WANG等[13]对物联网背景下产生的大量数据采用深度Q学习(Deep Q-learning, DQN)算法进行边缘卸载,有效减少了目标平均完成时间和所请求资源的平均数量的长期加权和,然而由于目标对象为多车任务,无法精确优化单实时任务的运行时间。
单实时任务是多任务协同调度的基本单元。上述学者针对多车任务协同调度取得了较多研究成果,但对具有数据依赖的单车推理任务调度研究不足。因此,本文考虑车辆行驶过程中不同实时推理任务与边缘环境的差异,设计边缘环境下的任务优化调度策略,从单任务角度出发优化运行时间。本文的主要贡献如下:
(1)提出针对推理任务的优先级判断方法,从而高效利用边缘节点,缩短任务执行时间。
(2)设计基于DQN算法的调度算法,在复杂边缘环境下探索更优的调度策略。
1 模型定义与分析
1.1 模型定义
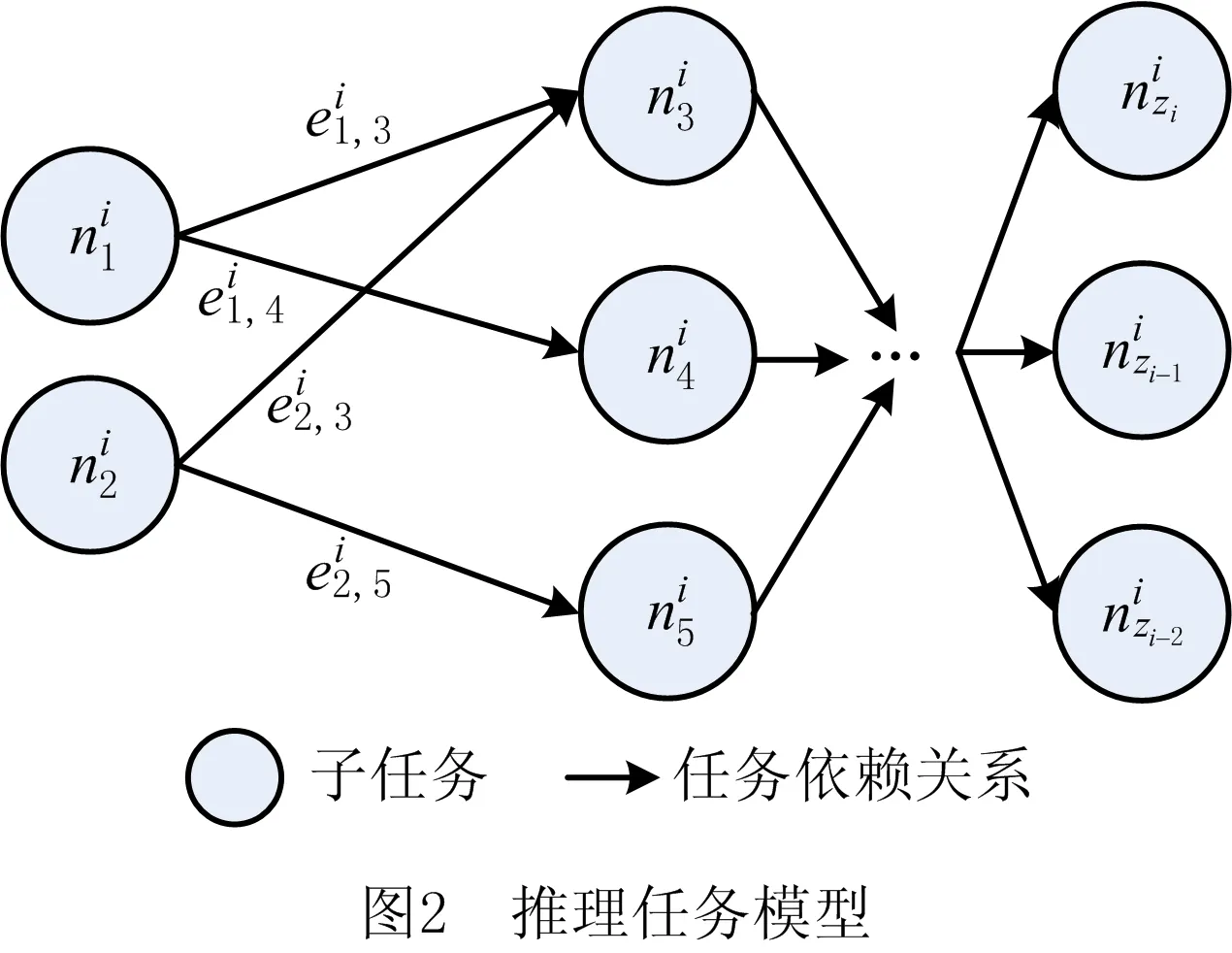
在车辆行驶场景下,自动驾驶等车载应用对实时性的要求愈发严格,充分利用边缘节点是有效减少其执行时间的关键,本文将复杂应用的推理过程构建为由若干存在依赖性的子任务组成的推理任务。在不同时间片中,随着车辆所处边缘环境的变化,可用的边缘节点数随之改变,等待调度的推理任务不尽相同。图1所示为推理任务和边缘节点数在不同时间片的状态。

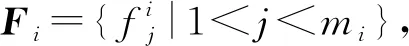
推理任务中,不同子任务的自身计算复杂度、任务数据量与对应的可容忍时延不尽相同,本文在实验中将其定义为
(1)

(2)

(3)
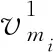
(4)

为了较好地利用不同边缘环境中边缘节点的算力,问题模型中规定边缘节点应满足以下规则:
(1)子任务能且仅能由单一边缘节点调度,定义为
(5)
(2)边缘节点需等待所有子任务传输完毕后方可开始计算。
(3)不同节点上的任务可并行处理。
(4)分配至相同节点上的子任务应按数据依赖关系顺序执行,若任务之间无数据依赖,则按照任务优先级正序执行。
(5)边缘节点上子任务的容忍时延不小于边缘节点的平均执行时间。
边缘节点正常工作时,实时任务的执行时间
(6)
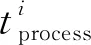
当边缘环境仅有一个边缘节点,即mi=1时,子任务将完全串行运行,为最差调度结果,完成时间
=1+MAX1≤x≤mi,1≤y≤zi(cx,y)。
(7)
综上所述,本文讨论的实时任务调度模型可以简单概括为:车载的实时任务在不同时间段内分配为若干个子任务;将子任务合理地分配给边缘节点处理,并计算实时任务的执行时间。本文所提调度算法使实时任务在约束下的执行时间最短,即
(8)
1.2 模型分析
图3所示为推理任务在特定边缘环境中子任务的分配情况,该场景下共有3个边缘节点{f1,f2,f3},划分为5个子任务{n1,n2,n3,n4,n5},存在5条有向边{e1,2,e1,3,e2,4,e3,4,e3,5}表示子任务的依赖性。图4所示为上述场景中一种可行分配策略(如表1)的实际执行过程,分配后的任务执行时间(如表2)为15 ms,包括4 ms传输时间(如表3);该场景最差的情况是串行任务的完成时间为1 ms,18 ms,19 ms;子任务的可容忍时延(如表4)满足大于节点中任务执行时间的条件,且子任务的执行顺序受子任务相对权重(如表5)的约束。
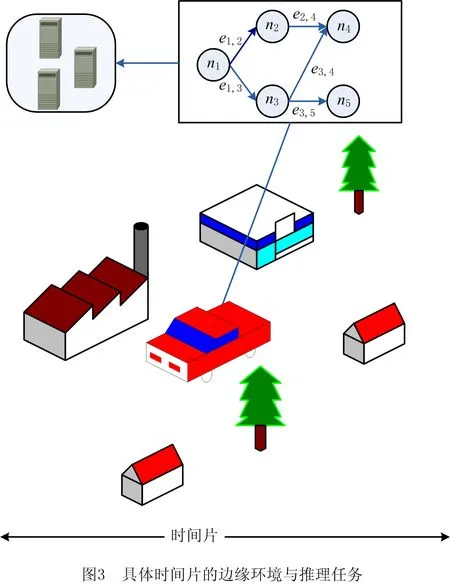
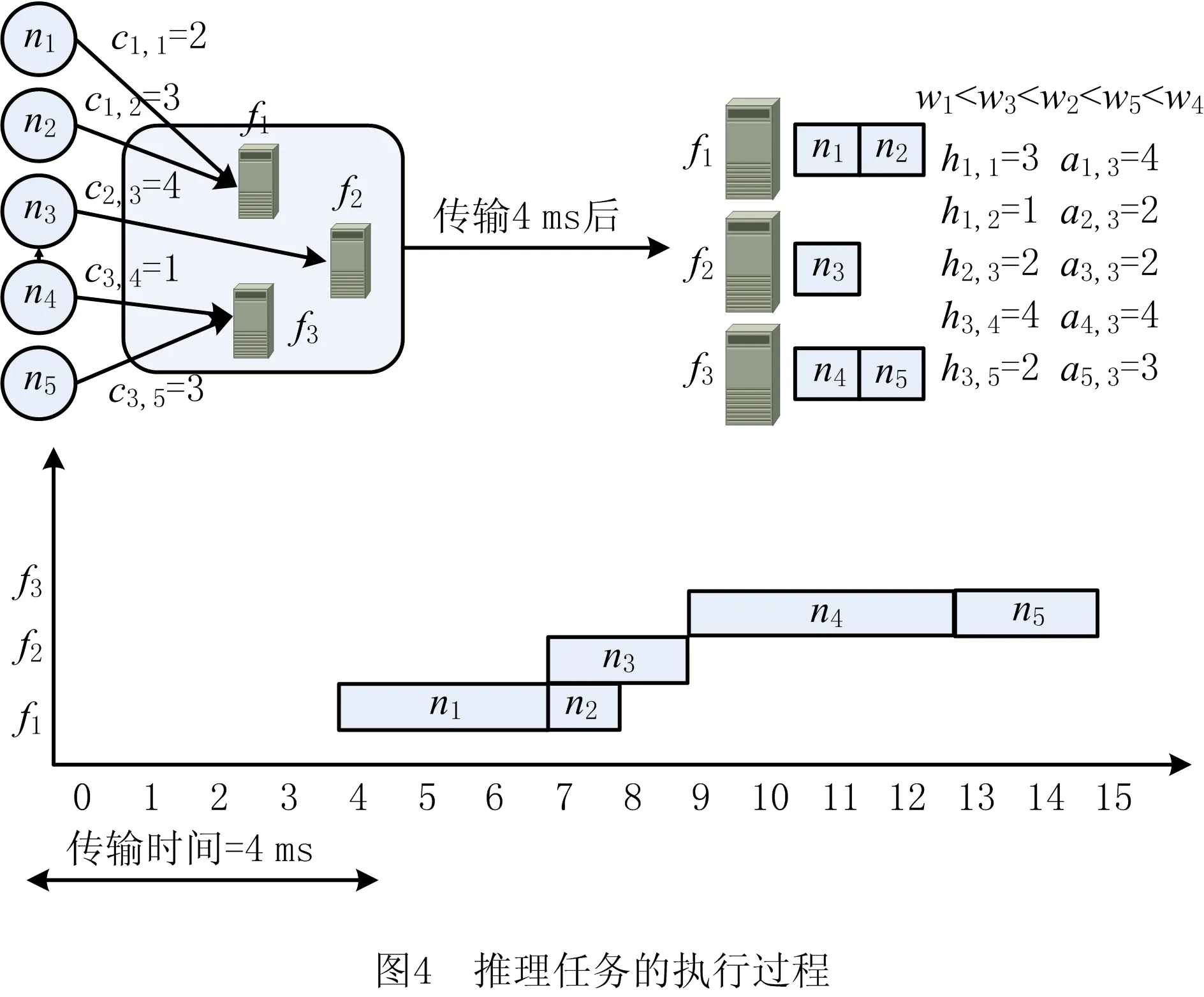

表1 边缘节点—子任务调度策略

表2 边缘节点平均任务执行时间 ms

表3 边缘节点的平均任务传输时间 ms

表4 子任务可容忍时延 ms

表5 子任务相对权重
2 算法设计
2.1 优先级评价
在同一计算节点中,可能存在相互之间无依赖关系的多个任务,这些任务的执行顺序会影响后续任务的执行情况。为解决该问题,本文采用模糊层次分析法衡量任务权重,然而该方法的原型为根据专家分值评估各个指标权重,存在较强的主观性。本文通过引入客观条件(子任务的实时信息)计算信息熵作为指标权重的补充修正条件,可有效解决该缺点,具体实现过程如下:
(1)按照三标度法原则
(9)
对子任务的α种因素进行重要性排序,构建优先关系矩阵P=(pi,j)α·α。其中si,sj分别表示指标pi,pj的相对重要程度,本文参与评价的指标有子任务自身计算复杂度、任务数据量和对应的可容忍时延。
(2)根据优先关系矩阵P构建模糊一致矩阵R,其中模糊一致矩阵R的定义为
R=(ri,j)α·α,
ri,j=ri,k-rj,k+0.5。
(10)
1)对优先关系矩阵P按行求和得ri,
(11)
2)由定义出发,ri可通过式(12)进行列变换,得到模糊一致矩阵R。
(12)
(3)对模糊一致矩阵R进行行求和与归一化,得到指标α对于各个子任务的指标权重wi,
i=1,2,…,α。
(13)
(4)利用隶属度函数式(14)对子任务自身因素Azi·3进行归一化:
(14)
(5)以归一化数据为基础,计算对应子任务zi的信息熵δi,
(15)
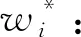
(16)
2.2 调度算法
马尔可夫决策过程(Markov decision process)是本文强化学习方法的基本模型,根据其性质,即下一个状态的产生只和当前状态有关,可简化调度策略模型,以下为本文研究问题模型的特点:
(1)状态空间 状态空间中的可行解状态数量不是恒定的,其随推理任务分解后子任务数量的改变以及不同时隙中边缘节点分布情况的不同而动态变化;状态空间中的一个可行解状态表示推理任务的一种可行调度策略,可行策略的定义是满足所有子任务的完成时延都低于各自的容忍时延,而且每个子任务能且仅能卸载到唯一边缘节点。
(2)动作空间 动作空间内可选的动作数等于子任务数zi,动作选择表示将当前状态中对应的子任务移动到到其他边缘节点。
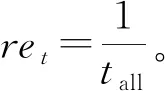
本文的调度策略基于DQN算法,是基于数值迭代的算法,其将深度学习与强化学习结合,可在状态与动作空间离散且维数较高的情况下将传统强化学习方法Q学习中建立Q列表的行为抽象为神经网络中不断训练参数的函数拟合问题。算法实现如算法1所示。神经网络的参数更新公式为:
Qk+1(st,at,θt)=Qk(st,at,θt)+αk·Rek;
(17)
式中:αk,γ分别为学习速率和折扣因子;Rek为迭代过程中累积的奖励值;s′为第k次迭代中执行at动作后的状态;a′为状态s′下奖励值最大的动作。
算法1任务—边缘节点调度算法。
输入:初始状态、最大回合数、单回合最大迭代次数。
输出:推理任务实时调度策略。
1:初始化恒定存储空间容量的经验池、随机权重为θ的动作—价值函数Qθ(st,at)和对应的target-Qθ(st,at)
2:for i←0 to最大回合数do
3: st←初始状态
4: for i←0 to单回合最大迭代次数do
5:以ε的概率选择历史奖励值最大的动作at=argmaxQ(st,a,θ),否则选择随机动作at
6: 执行动作at,得到下一个状态st+1,并利用算法2计算奖励值ret
7:将(st,st+1,ret,at)存入经验池
8:st←st+1
9: 经验池中随机抽样(sj,sj+1,rej,aj),
10: 根据式(17)构建误差函数,反向传播更新参数θ
11: 每若干步更新target-Qθ(st,at)=Qθ(st,at)
12:若st+1满足终止状态,则结束本轮迭代
13:end for
14:end for
2.3 执行算法
在不同时间段,实时任务和边缘环境是动态变化的,概括为如下3种情况:
(1)实时产生推理任务拓扑结构与所处边缘环境可通信的边缘节点数。
(2)不同环境下子任务的计算复杂度、任务数据量与可容忍时延的变化。
(3)由边缘节点变化导致的子任务传输时间与运行时间的改变。
本文提出的执行算法可计算边缘环境中的推理任务完成时间,其实现如算法2所示。
算法2任务执行算法。
输入:mi,zi,Gi,Azi×3,Bmi×zi,Cmi×zi,Hmi×zi。
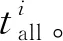
1:初始化:设置数组I、子任务队列Q以及子任务的前驱节点集合R为∅
2:利用约束关系Gi设置数组I(i)
3:将数组I(i)=0的第i个子任务加入队列Q,设置遍历的子任务数u=0,设置当前层k中子任务数量等于当前队列大小
4:while Q!=∅ do
5: if u=k then
6: u=0,k=size(Q)
7:endif
8: 子任务出列,任务表示为v,u+=1
9: for i←0 to zido
10: if ∀v到i的有向边then
11:将第v个子任务及其前驱节点集合R(v)添加到R(i),I(i)-=1
12: if I(i)=0 then
13:将第i个子任务添加到Q队列中
14:end if
15: end if
16: end for
17:end while
18:根据Bmi×zi将子任务分配给边缘节点,同边缘节点的子任务按照前驱任务是否完成的约束条件执行,若同边缘节点中子任务的前驱任务均已完成,则目标子任务按照子任务优先级大小从高到低顺序执行。
19:初始化:设置子任务完成列表O为∅,用Cmi×zi设置子任务Y的剩余执行时间,设置当前运行时间h=0
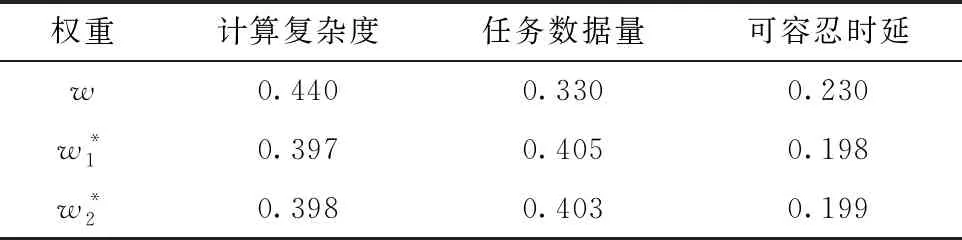
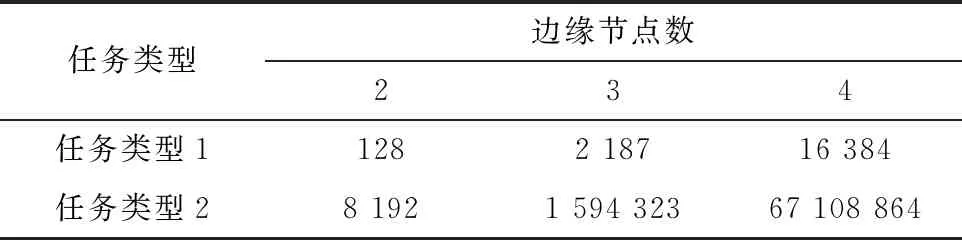
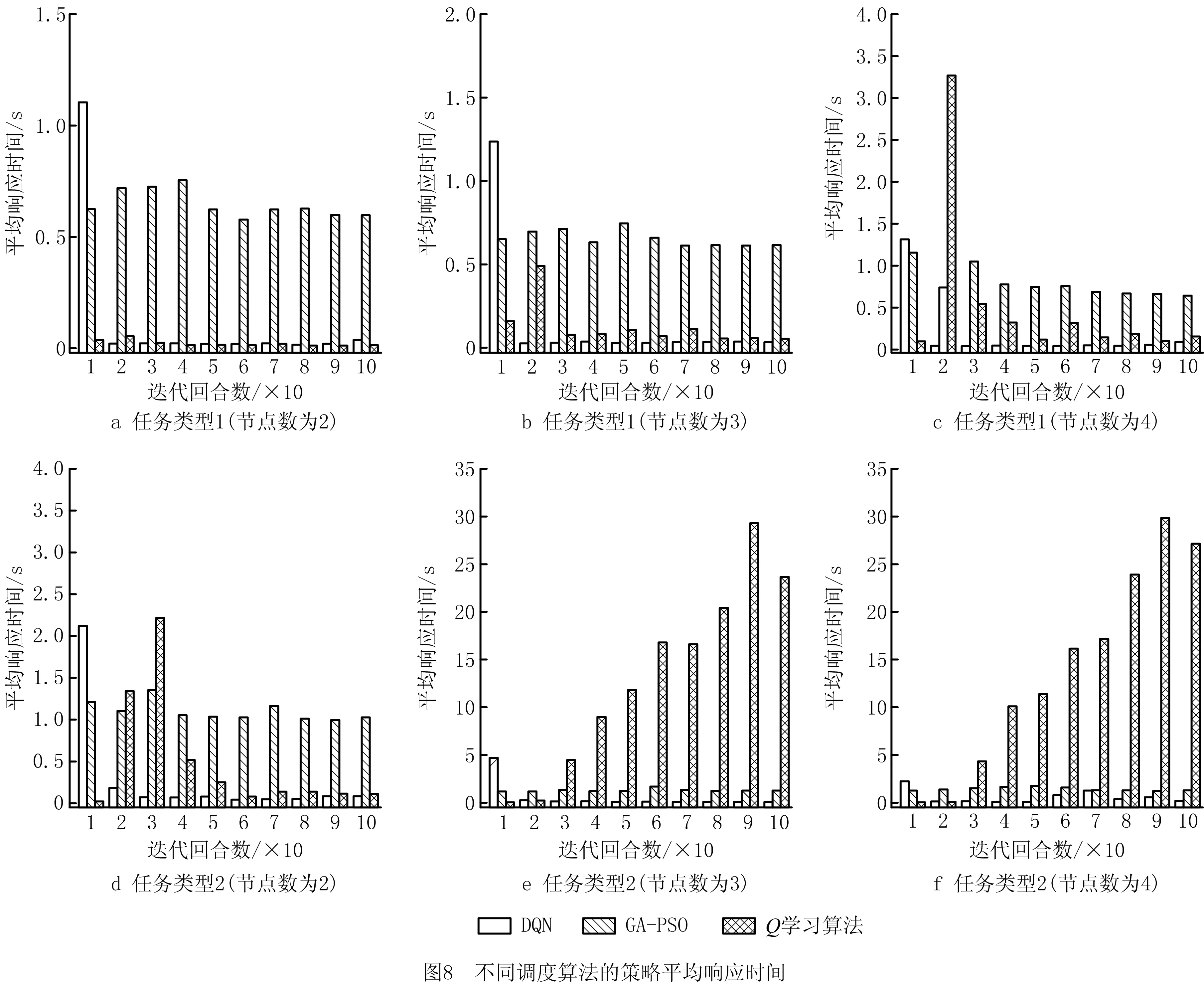
20:while O 21: 确定分配到每个边缘节点的子任务,满足对应子任务的直接前驱集合是完成列表O的子集 22:从当前并行执行的子任务中找到最小执行时间w 23: 设置边缘节点的子任务Y(i)-=w,当Y(i)=0时,将第i个子任务添加到O,设置h+=w 24:end while 25:return h 本文模拟实验在Python 3.7环境下实现,实验设备为Inter(R) Core(TM) i7-7700HQCPU,16 GBRAM的64位Win10系统,为检验所提基于DQN算法的调度策略性能,对比算法选用传统强化学习Q学习算法[10]与基于遗传算法改良的粒子群优化算法(Particle Swarm Optimization with Genetic Algorithm,GA-PSO)[14]。实验中所有算法的目的均为寻找完成时间最短的可行分配策略。 实验仿真参数按照IEEE 802.11p车辆网络场景标准设定[15],具体设置如表6所示;仿真实验对象为边缘环境下的同类型实时任务,拓扑结构如图5所示,具体设置如表7~表9所示。 表6 仿真实验约束参数 表7 边缘节点传输速率和算力 表8 仿真任务与场景参数 表9 自身因素的权重 为测试任务调度策略的可行性,将拓扑结构不同的推理任务分别卸载到边缘节点数不同的边缘场景,计算其最优分配时的任务完成时间。如图6所示,由于调度策略中的边缘节点数决定任务同时间片下的最大可并行任务数,开始时任务的完成时间随节点数的增多明显下降;当满足边缘节点数大于等于最大可并行任务数时,任务的完成时间相同。相比按照任务深度顺序执行的策略,本文所提结合优先级评价的任务执行算法对任务完成时间的优化较明显。 为测试调度算法在实时环境下的收敛性,在边缘环境下对同一任务分别用GA-PSO、Q学习、DQN算法进行卸载。实验对不同边缘环境分别进行100回合测试,将每10回合的策略取均值,结果如图7所示。对任务类型1而言,GA-PSO在多种边缘环境下都能找到时延表现较好的解,然而该算法搜寻最优解的过程依赖于粒子种群的随机搜索,因此较难收敛;Q学习和DQN算法在经过前期若干回合学习后,可找到完成时间更短的解,且收敛性良好。对于任务类型2,GA-PSO的表现与求解任务类型1相似,每回合虽然可以找到较可观的次优解,但是存在陷入局部最优的情况;Q学习在边缘节点数为2的场景下表现良好,在节点数增加至3,4时难收敛;DQN在所有边缘场景下均表现优秀。 图7出现异常可能是子任务数量增加使策略解空间倍增的原图。如表10所示,对于庞大的离散解空间,GA-PSO在限制时间开销的场景下易陷入局部最优;Q学习的核心操作为创建Q列表,然而庞大的可行解空间导致其状态数出现维度爆炸,Q列表难以存放如此多的可行解,从而使算法难以收敛;与其相比,DQN利用神经网络将Q列表近似拟合成Q值函数,解决了上述Q学习方法的难题,因此更易收敛。 表10 策略空间数量 为测试调度算法在实时环境下的有效性,分别采用GA-PSO、Q学习、DQN算法在不同边缘环境下卸载同一实时任务,在每个边缘环境进行100回合测试,并将每10回合的实时响应时间取均值,结果如图8所示。可见,GA-PSO在各个场景下对不同任务的响应时间均较稳定,原因是其搜索策略的速度仅由所用的探索粒子数决定;Q学习和DQN算法在回合数较前时,由于需要大量可行策略进行学习,响应时间较长,随着回合数的增多,在收敛的情况下响应时间逐渐下降,而且DQN算法稳定收敛时的响应时间较Q学习更短。 本文提出一种基于DQN算法的车载推理任务的实时调度策略,通过分析不同边缘场景下实时任务的完成时间,证明所提策略可充分利用边缘节点的计算能力,其能够随节点数的增加显著降低实时任务的完成时间。通过对比相同类型任务在不同算法下的性能发现,在复杂度较低的任务下,GA-PSO、Q学习、DQN算法都能在较短时间内提供有效的任务调度策略,但GA-PSO的收敛性略差;针对复杂度高、边缘环境复杂的任务,Q学习的收敛性极差,GA-PSO较差,DQN方法表现优越。通过实验对比实时响应时间表明,相比响应时间稳定的GA-PSO算法,随样本数量增加不断改善的强化学习方法在实时性要求苛刻的车载背景下表现更好。 未来研究考虑将本文工作拓展至具有复杂推理任务的多车辆协同调度场景,以缓解同一边缘环境下多车任务资源分配不均的情况;另外,将持续改进调度算法,优化神经网络结构与训练效率,并在系统模型中加入信道波动、无线电干扰等复杂环境因素。3 仿真实验与分析
3.1 实验参数设置




3.2 实验结果分析


4 结束语

