基于正则化约束元学习优化器的深度学习模型

周靖洋 曾新华

1(中国科学院合肥物质科学研究院合肥创新工程院智能感知中心 安徽 合肥 230031) 2(中国科学技术大学 安徽 合肥 230026) 3(复旦大学工程与应用技术研究院 上海 200433)

0 引 言

深度学习在许多领域都取得了巨大的成就，如图像识别和自然语言处理等，但同时也出现了许多问题，如用传统深度学习优化器训练的模型，在训练数据集上表现很好，却无法在测试集上取得同样的效果，造成了过拟合；在面对对抗攻击[1]时，模型会做出错误的判断，导致识别受到干扰，且稳定性降低。因此如何提高模型的泛化能力和鲁棒性，成了许多研究者的研究重点之一。

泛化能力和鲁棒性是深度学习模型重要的评价指标。近年来不断发现，深度学习模型损失函数在更加平坦局部最小值时，有着更好的泛化能力[2]，不同优化器的选择就是一种对初始化参数的正则化约束，可以得到更加平缓的局部最小值[3]。通过减小梯度的急剧变化，可以使损失曲线变得平缓，从而获得更好的测试准确率[4]，也意味着具有更好的泛化能力。深度学习模型在学习的时候，通常会利用数据中的所有特征，甚至那些人眼所感知不到的特征[5]，更平缓的局部最小值可以让深度学习模型更快地学习到这些数据的总体特征，得到更好的鲁棒性。近年来学术界对元学习和梯度之间的关系[6-7]以及优化器与“平缓”的局部最小值之间的关系[8-9]都进行了大量研究。因此，选择一个可以使模型拥有“平缓”的局部最小值的优化器，对模型的泛化能力和鲁棒性来说，显得十分重要。

借鉴元学习[10]的思想，本文通过研究元学习优化器的训练和优化过程，分析了元学习的内部机理，提出了四种针对元学习优化器的正则化约束，使得在元学习优化器训练时，抑制模型参数的剧烈变化，得到更平缓的局部最小值。本文证明了经过正则化约束训练的元学习优化器(记为Meta-reg)，同未加入正则化约束训练的元学习优化器(记为Meta)、Adam、Adagrad和SGD相比，在两层、四层CNN的Mnist分类上，提升了泛化能力；在两层、四层CNN的Cifar10分类上，提升了在FGSM、PGD攻击下的鲁棒性。同时分析比较了四种不同的正则化约束的实验结果，表明：在两层CNN的Mnist分类上，用Hessian矩阵的特征谱密度作为正则化约束，在提升泛化能力上最好；在四层CNN的Mnist分类上，Hessian矩阵的迹作为正则化约束，在提升泛化能力上最好。

1 正则化约束训练的元学习优化器

元学习的思路是先让系统学习任务的先验知识，再让系统去驱动全新的任务，元学习目前的主要实现方式有三种：基于长短记忆神经网络(LSTM)、基于强化学习和基于注意力机制的方法。原理如图1所示。

元学习优化器则是由待优化的问题(记为optimizee)来驱动，再应用到不同的问题中。

结合元学习的思想，将基于梯度下降的优化问题作为训练任务，让机器经过一定的优化训练，学会梯度下降，从而得到元学习优化器。其相对于传统的优化器，具有设计简便、优化效果好的优点。下面将主要介绍基于LSTM[12]神经网络的元学习优化器的原理和如何加入正则化约束训练元学习优化器。

1.1 元学习优化器

LSTM神经网络可以选择性地记忆或丢弃一些信息，在时间序列的处理上有着广泛的应用，而梯度下降算法也是一种基于时间序列的算法，因此元学习优化器的工作原理就是：将待优化问题的梯度输入LSTM中，再让LSTM根据之前选择性保留的梯度信息，输出一个更新值，通过这个更新值更新待优化问题的参数，从而实现优化的过程。

1.1.1实验的元学习优化器选择

Andrychowicz等[13]设计了一个两层LSTM的元学习优化器，隐藏层大小都是20，用它迭代optimizee 100次，得到对应的100个optimizee损失值并求和，通过用Adam迭代更新元学习优化器的参数，使得这100个optimizee损失值之和最小化，得到元学习优化器。

Wichrowska等[14]提出了一种梯度下降的控制器作为元学习优化器，得到optimizee的梯度后，控制器根据梯度输出学习率，再通过学习率，输出最终的更新值，更新optimizee。控制器由三层LSTM网络组成，第一层LSTM处理optimizee每一个参数，第二层LSTM处理第一层LSTM的参数，第三层LSTM处理第二层LSTM的参数，这样通过分层的LSTM实现对梯度信息更加有效的管理和控制。

相比于文献[13]，文献[14]的方法收敛性更好。实验采用文献[14]方法的元学习优化器作为Meta，并在其基础上，加入正则化约束训练后得到Meta-reg。

1.1.2元学习优化器的训练过程

训练一个元学习优化器，让元学习优化器优化optimizee，即对optimizee的参数迭代一次，得到optimizee的损失值lp，将若干个lp求和得到元学习优化器的损失值LO，通过不断降低LO，得到训练的元学习优化器。LO的计算原理如下：

(1)

式中：PO为元学习优化器的参数；ope为optimizee；n为optimizee的迭代次数；w为optimizee的参数；d为输入optimizee的数据样本。训练一个元学习优化器，即为不断更新迭代PO，使得LO(PO,ope)降低，原理如下：

M=argminLO(PO,ope)

(2)

式中：M为训练好的元学习优化器。流程如图2所示。

1.2 正则化约束

对于大型神经网络而言，单纯使用梯度下降算法，由于参数量过多，并且远超过训练样本，因此很容易陷入过拟合的情况，造成泛化能力差，结果在训练集上表现很好，却在测试集上表现差。采用正则化约束后，可以让它避免陷入过拟合的情况。经典理论认为，机器学习模型之所以会陷入过拟合，就是因为模型的损失值进入了相对“陡峭”(梯度值大)的局部最小值，只有使得“陡峭”的局部最小值变得“平缓”，才能抑制模型的过拟合和提升泛化能力。因此通过在原有的损失值上加入一个惩罚项，抑制梯度往陡峭的局部最小值方向下降，使得模型最终进入一个相对平缓的局部最小值。

由于元学习优化器本质上也是一种深度学习模型，通过加入正则化约束，可以让训练出来的元学习优化器在优化optimizee时，可以进入更加“平缓”的局部最小值。为此本文提出在元学习优化器上加入正则化约束的方法，使其在优化深度学习模型的时候，让模型拥有“平缓”的局部最小值，进而提高模型的泛化能力和鲁棒性，即在LO上加上正则化约束项来进行训练。

本实验提出的正则化约束分为以下两类。

(1) Hessian正则化约束。Hessian正则化约束可由optimizee的Hessian矩阵计算得来。Hessian矩阵计算式为：

(3)

式中：y为optimizee的损失值；x1,x2,…,xn为optimizee的所有参数；H为Hessian矩阵。

Hessian正则化约束有三种，即Hessian矩阵的迹(trace)、Hessian矩阵的最大特征值(eigen value)、Hessian矩阵的特征谱密度(eigen spectral density)，它们按照Yao等[15]的方法计算而来。

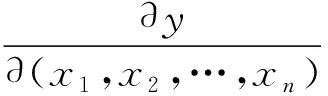
研究采用Hessian矩阵的迹(trace)、Hessian矩阵的最大特征值(eigen value)、Hessian矩阵的特征谱密度(eigen spectral density)和雅可比行列式四种正则化约束方式。通过正则化约束，元学习优化器在选择梯度下降方向的时候，便会受到梯度值的约束，而无法沿梯度值最大的方向进行更新，只能沿梯度较为平缓的方向进行更新，从而更好地抑制过拟合，并取得更好的泛化能力。

为此在optimizee的迭代过程中的损失值上，加入正则化约束项，作为最终的LO，则：

(4)

式中：α为正则化项的系数；reg为正则化约束项。流程如图3所示。

1.3 模型的泛化能力

深度学习模型在未知数据集上取得的表现，称为泛化能力，选择测试准确率以及测试、训练准确率之差，作为泛化能力的比较指标。

1.4 模型的鲁棒性

深度学习模型在遭到对抗攻击时，输出会产生巨大的偏差，因此提高模型鲁棒性非常重要。

对抗攻击是在原始数据样本中，加入对抗干扰因素后，生成对抗样本，并输入到训练好的网络中，诱导其做出错误的判断。其原理可用式(5)表示。

d^=d+σ

(5)

式中：d^为对抗样本；d为原始数据样本；σ为对抗干扰。目前主要有两种对抗攻击方式，即FGSM和PGD。

FGSM原理可用式(6)表示。

σ=e·sign(▽dl(w,d,s))

(6)

式中：e为迭代步长；l(w,d,s)为模型的损失值；▽d为l(w,d,s)对d求导的梯度；sign为▽d的方向；w为模型的参数；s为原始数据样本对应的标签。

FGSM的目的在于：通过梯度上升，在原始数据样本上加入对抗扰动，使得模型的损失值增大，从而做出错误的判断。

PGD也称为K-FGSM，即反复迭代K次FGSM的过程，由于PGD相比于FGSM对非线性模型的迭代方向有着更好的适应性，所以PGD的攻击效果要远好于FGSM的攻击效果。实验中K选择为10。模型在对抗样本上取得的准确率越高，则鲁棒性越好。

2 实验过程

2.1 实验设计

实验模型选择：Hornik等[16]提出了通用近似理论证明，拥有无限神经元的单层前馈网络，能逼近紧致实数子集上的任意连续函数，只要网络足够复杂，则可以拟合任意连续的实数函数。Bengio等[17]研究了更深层的网络比浅层的网络有更好的函数拟合能力，通过增加网络的层数使得网络更加复杂，增加网络的拟合能力和表征能力，提升网络的效果。Montufar等[18]的研究表明在同样的参数量下，深层网络有着比浅层网络更好的非线性，可以取得更好的效果。因此本文选择在两层和四层CNN上进行实验，用于更深层的网络上，也可以取得更好的效果。

实验分成三步：(1) 在optimizee上训练Meta-reg；(2) 得到训练好的Meta-reg后，再用Meta-reg在测试问题上测试，得到训练好的测试问题模型，独立重复10次；(3) 从训练好的测试问题模型中，选择测试准确率最高的一次，进行模型鲁棒性测试。

训练optimizee在两层CNN的Mnist分类上进行。泛化能力测试分别在两层、四层CNN的Mnist分类上进行，鲁棒性测试分别在两层、四层CNN的Cifar10分类上进行(在两层CNN的Mnist、Cifar10分类中，每层卷积核个数均为16；在四层CNN的Mnist、Cifar10分类中，每层卷积核个数均为32。激活函数为ReLU)。两层和四层CNN的结构分别如图4和图5所示。

实验在英伟达RTX2080ti上进行，选择数据集为Mnist，批大小为64，Meta-reg训练epoch数为5，用Rmsprop训练Meta-reg，学习率为。所有optimizee的参数均为正态随机初始化，采用交叉熵作为损失函数。

2.2 训练Meta-reg

从Mnist的训练集中随机采样出10 000个训练样本，按批输入到训练optimizee中，Meta-reg对optimizee的参数进行一次迭代得到lp，并在lp上加上对应的正则化约束项reg，得到正则化损失值，将300次迭代过程的正则化损失值求和，作为Meta-reg的损失值，用Rmsprop对Meta-reg的参数进行更新迭代，使其不断降低，训练5个epoch后，得到训练好的Meta-reg。实验中通过不断地调整正则化项系数α，使得正则化约束获得最好的效果，依次得到对应的四种Meta-reg。

2.3 测试Meta-reg

训练好Meta-reg后，分别在两层、四层CNN的Mnist分类上，训练100个epoch，独立重复进行10次，取测试准确率最高的一次，进行比较(Meta、Adam、Adagrad和SGD的测试过程同理)。在两层、四层CNN的Cifar10分类上，测试过程同理。

3 实验结果

3.1 泛化能力

3.1.1两层CNN的Mnist分类的泛化能力

将Adam、Adagrad、SGD、Meta和Meta-reg在两层CNN的Mnsit分类上的实验结果进行比较，结果分别如图6-图9所示。其中：图6和图7分别是测试准确率总曲线和其细节展示；图8和图9分别是测试、训练准确率之差的总体曲线及其细节展示。

3.1.2四层CNN的Mnist分类的泛化能力

将Adam、Adagrad、SGD、Meta和Meta-reg在四层CNN的mnsit分类上的实验结果进行比较。泛化能力比较结果如图10、图11、图12和图13所示，其中：图10是测试准确率总体曲线；图11是测试准确率的细节展示；图12是测试、训练准确率之差的总体曲线；图13是测试、训练准确率之差的细节展示。

3.2 模型鲁棒性

3.2.1两层CNN的Cifar10分类上的鲁棒性比较

依次选择Meta、Adam、Adagrad、SGD和Meta-reg在两层CNN的Cifar10分类上，测试准确率最高的模型，进行鲁棒性比较。先用FGSM分别对Meta、Adam、Adagrad、SGD和Meta-reg的模型，进行对抗攻击测试，对抗样本按照epsilon从0.1/255、0.2/255、0.3/255、0.4/255、0.5/255的顺序生成，测取模型对抗攻击的准确率，PGD过程同理。实验结果见表1、表2。

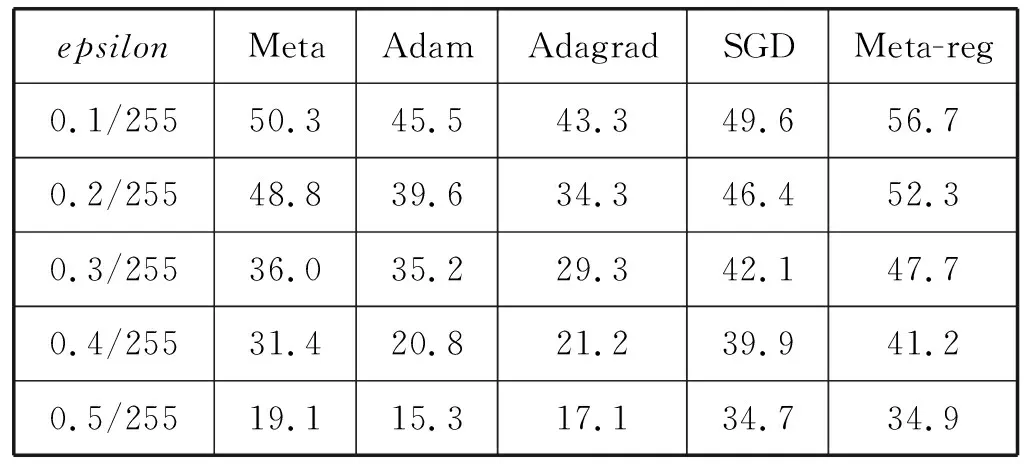
表1 不同优化器训练的两层CNN在FGSM

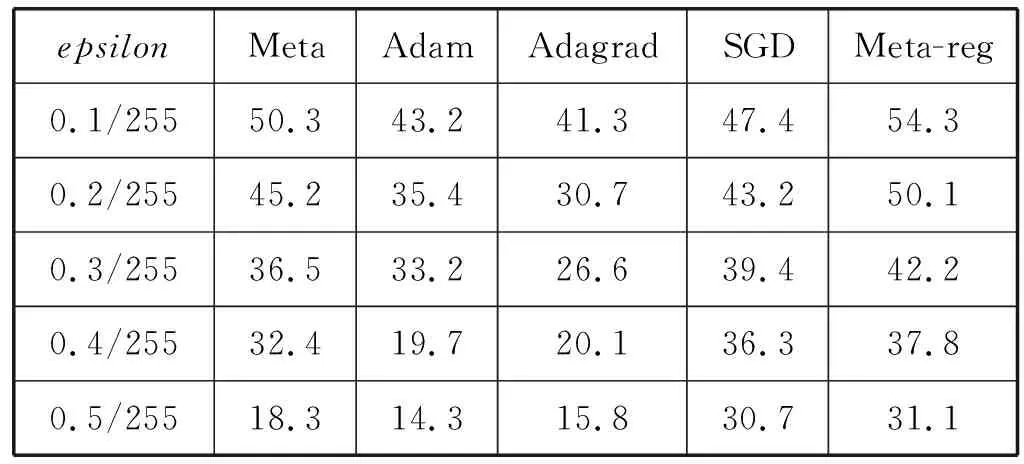
表2 不同优化器训练的两层CNN在PGD

3.2.2四层CNN的Cifar10分类上的鲁棒性比较

依次选择Meta、Adam、Adagrad、SGD和Meta-reg在四层CNN的Cifar10分类上，测试准确率最高的模型，进行鲁棒性比较。先用FGSM分别对Meta、Adam、Adagrad、SGD和Meta-reg的模型，进行对抗攻击测试，对抗样本按照epsilon从0.1/255、0.2/255、0.3/255、0.4/255、0.5/255的顺序生成，测取模型对抗攻击的准确率，PGD过程同理。实验结果见表3和表4。

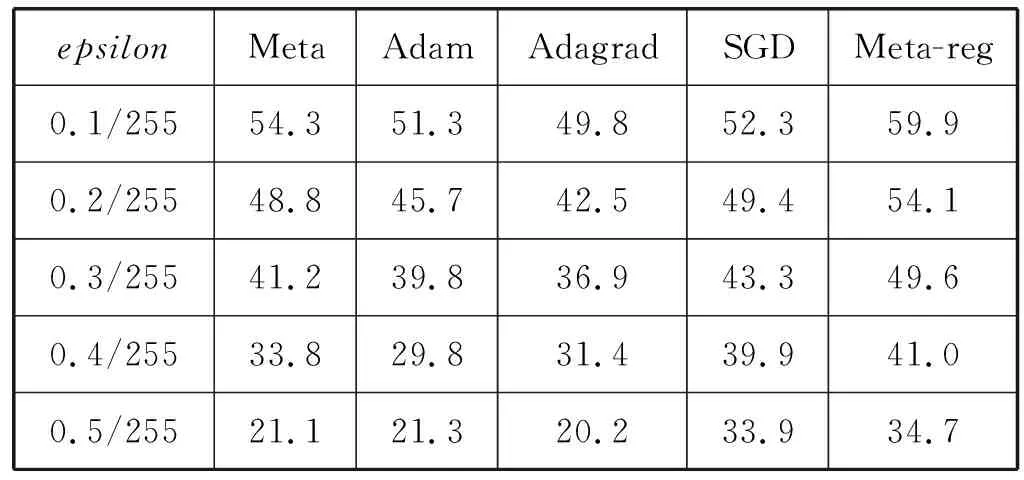
表3 不同优化器训练的四层CNN在FGSM

表4 不同优化器训练的四层CNN在PGD

3.3 不同正则化约束作用之间的比较

实验以Meta作为基准参考对象，与加入四种不同的Meta-reg进行比较，其中Hessian矩阵的特征谱密度、Hessian矩阵的最大特征值和Hessian矩阵的迹分别记为Meta-Hessian-EV、Meta-Hessian-ESD、Meta-Hessian-Trace，Jacobian正则化约束记为Meta-Jacobian。在两层CNN上进行的实验结果，分别如图14、图15所示，在四层CNN上实验的结果分别如图16、图17所示。

4 结果分析

以上结果表明，加入了正则化约束训练后的元学习优化器，与其他优化器相比，在两层和四层CNN上，Meta-reg在泛化能力上均明显优于其他的优化器，随着epoch的增加，测试、训练准确率之差曲线始终保持相对平稳，并且低于其他优化器，测试准确率也比其他优化器的结果更好。四层CNN与两层CNN相比测试准确率提升了0.5%，而且已有研究[16-18]证明，神经网络有着拟合任意函数的能力，这种拟合能力会随着其层数加深，而越来越好。因此，实验的方法能在更复杂的神经网络上取得很好的效果。

在对抗攻击的鲁棒性方面：在两层、四层的CNN的Cifar10分类上，用FGSM按epsilon为0.1/255、0.2/255、0.3/255、0.4/255、0.5/255分别进行对抗攻击，用Meta-reg训练出来的模型均有最高的鲁棒性，同样用PGD按epsilon为0.1/255、0.2/255、0.3/255、0.4/255、0.5/255分别进行对抗攻击，用Meta-reg训练出的模型均有最高的鲁棒性。四层CNN与两层CNN相比，在FGSM和PGD对抗攻击下，鲁棒性更好。

图14、图15实验结果表明，在两层CNN的Mnist分类上，用Hessian矩阵的特征谱密度作为正则化约束，在泛化能力上最好；图16、图17实验结果表明，在四层CNN的Mnist分类上，Hessian矩阵的迹作为正则化约束泛化能力最好。

5 结 语

本文对近年来深度学习所面临的过拟合和易受对抗攻击等问题，结合当前新兴的元学习优化器，通过研究元学习优化器的原理，研究并提出四种正则化约束，用于训练元学习优化器，使得Meta-reg在训练深度学习模型时，提高了模型的泛化能力和鲁棒性。并且在两层、四层CNN的Mnist分类问题上，Meta-reg都比其他优化器具有更好的泛化能力。

在两层、四层CNN的Cifar10分类上，用FGSM和PGD进行对抗攻击后，Meta-reg训练出的模型都有最高的鲁棒性。

通过对不同的正则化约束实验进行比较发现：在两层CNN上，Hessian矩阵的迹约束效果最好；在CNN网络上，Hessian矩阵的最大特征值约束效果最好。

以上研究和实验表明，通过精心设计的正则化约束项训练后，相比其他优化器，Meta-reg训练的深度学习模型取得了最好的泛化能力和鲁棒性，用于更复杂的深度学习模型效果会更好。