改进的深度卷积网络在医学图像中的研究应用

舒 晖 王以伍

(成都医学院现代教育技术中心 四川 成都 610500)

0 引 言

随着医学影像技术的发展，医学图像的应用在医学领域中日益重要，合理有效的医学图像可以真实反映人体组织器官的形态结构信息，为医务工作者对病理判断提供直观的依据[1]。但是医学图像在采集、生成和传输过程中，受工作环境、仪器设备等因素的影响，不可避免地产生噪声。噪声的存在导致医学图像中组织结构的形态及颜色深浅发生畸变，容易误导医务工作者对图形边缘及纹理细节的识别，从而对病理形成误判，增加误诊的风险。因此，为获取真实可靠的医学图像，必须消除医学图像噪声，给医疗诊断提供有效资料，提升诊疗水平。

目前，传统的图像去噪方法在医学图像处理中应用已久，例如基于变换域的去噪方法[2-3]、基于滤波器的去噪方法和基于统计学信息的去噪方法等[4]。但是上述方法的去噪结果大都不尽如人意[5]，在噪声压制和细节保持之间很难同时兼顾，距离医学图像的去噪标准仍有差距。

近几年的深度学习技术得到广泛发展与应用，相比较传统去噪方法，深度学习通过神经网络的学习训练具有很好的去噪效果，目前在图像处理中逐步得到推广。尤其是Zhang等[6]提出的DnCNN(Denoising convolutional neural networks)算法，是目前最为有效的图像去噪算法之一。但该算法采用单一尺度的卷积核，容易导致去噪结果丢失局部细节信息，造成边缘/纹理等模糊，不利于图像质量的提升，在医学图像处理方面依然存在不足，需要进一步改善。针对上述不足，先后有学者从网络的结构设计方式进行改进，例如采用Alex网络、VGGNet(Visual Geometry Group Net)等[7]，也有学者采用并行计算等方式用于提升计算速度[8-9]，但是上述方式并没有从根本上解决算法不足，其去噪效果提升不大。文献[10-11]将空洞卷积引入深度学习网络中，代替原有网络中的传统卷积，形成空洞卷积神经网络(Iterated dilated convolution neural networks，ID-CNN)，新的学习网络具有较好的去噪能力，去噪结果保留更多的细节信息，但是由于参数多、网络深，导致训练时间长，计算效率低。

本文在DnCNN算法的基础上，对网络结构进行改进，建立一种多尺度卷积核提取图像特征的残差网络，增加网络对多尺度特征的感知能力，同时改进网络损失函数和激活函数，在网络中添加跳跃连接，提高算法的去噪效果和细节保护能力，提升计算效率。为验证本文方法的有效性，将其与曲波变换算法、BM3D算法、DnCNN算法、ID-CNN算法进行对比。结果表明本文方法具有更好的去噪效果，边缘/纹理细节保留更为完整，图像更为清晰，具有较好的应用效果。

1 方法原理

1.1 DnCNN算法原理

常规卷积神经网络进行图像去噪时，通过学习无噪图像进行目标图像的去噪。而DnCNN采用深层次的卷积神经网络结构对含噪图像的噪声进行学习，应用批归一化技术和线性整流函数提升训练深度[12]，求取期望噪声残差和网络计算噪声残差之间的误差，实现图像噪声的去除。模型流程如图1所示，左侧表示输入含噪图像，最右侧表示通过残差学习后的输出噪声。

1.1.1残差学习

DnCNN算法进行图像去噪时，通过学习含噪图像，对网络输出结果和输入图像进行对比并计算两者残差，并最小化该残差的代价函数，则DnCNN模型的代价函数为：

(1)

式中：hw,b(xi)表示在训练集xi情况下神经元的输出；yi表示输入的含噪数据集；m表示测试样本数。则整个网络的代价函数为：

(2)

式中：Θ表示训练参数；R表示图像残差；x表示预测结果图像；y表示输入含噪图像；n表示网络模型中输入图像的Patchs数目。然而，常规深度网络受相关条件限制，在网络层数增加时，反向传播容易衰减梯度信息，导致训练结果很难收敛。但是DnCNN深度残差网络从网络结构上解决上述问题，对残差学习策略进行优化，从而更好地应用于深度网络中[13]，更有利于深层网络的优化与提速。

1.1.2批归一化

Ioffe等[14]首次提出批归一化概念，并用于解决深度网络中白化操作的低效率等问题。随着网络层数增加以及模型的深化，多个函数或多个网络层数的组合被应用在模型建立过程中。但是，初始输入层的微小变化会引起后续深层网络的剧烈变化，导致网络的学习效率、更新策略以及初始权重选择建立更为困难。针对上述深度学习的内部协变量转移问题，归一化方法可以有效解决。

深度学习通常要求输入数据满足独立分布的条件，从而提高模型准确度。当一组向量x=(x1,x2,…,xm)输入至单个神经元时，通过网络函数计算得到一组数据yi=f(xi),i=1,2,…,m，为使输入数据达到独立分布条件，需要对每一层网络的数据进行白化操作，且保证深度网络反向传播实现梯度的更新。因此，在输入向量x传递给神经元之前，需要对向量进行平移伸缩变化，使输入向量的分布满足标准分布的形态，则变化后的输入向量x变为：

(3)

式中：g、σ表示缩放因子；μ、b表示平移因子；m表示样本数目。通过式(3)使最终的输入向量满足均值为b，方差为g2的分布，且使得下一层网络的输出结果同样满足上述分布条件。在深度网络学习中，上述变化因子是自适应变化，从而有效保证各层深度网络学习的有效性，提升深度网络的非线性表达能力[15]。

在针对输入向量的标准化时，通常采用对mini-batch数据进行训练，计算单个神经元当前输入向量的均值μi和方差σi，其计算公式为：

(4)

(5)

式中：m表示向量的维数，也表示mini-batch的大小；ε为无穷小的正值。在进行网络的反向传递时，用上述公式进行输入向量X的标准化。

1.1.3损失函数

损失函数又叫误差函数，表示预测图像和输入图像之间的差异，用以衡量网络的训练学习情况。DnCNN算法采用均方误差函数作为损失函数，通过卷积网络训练实现损失函数的最小化，其表达式为：

(6)

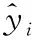
1.2 DnCNN算法的改进

由上述方法原理可以发现DnCNN深度残差网络的训练效率较低，收敛速度和精度有待于进一步提高。而最新的ID-CNN网络由于参数多、网络深，导致训练时间长，计算效率低。针对上述情况，本文基于原有DnCNN算法原理，采用一种不同尺度卷积核提取层提取图像的不同尺度特征，增加网络对不同尺度的适应性，对损失函数和激活函数进行优化，并在网络中添加跳跃连接，加快网络训练速度，提升网络收敛精度，从而实现改善图像结果的目的。

1.2.1多尺度特征提取

为更好地获取浅层特征，本文采用一种多尺度特征提取层，采用3×3、5×5、7×7三种尺寸大小的卷积核，从而对不同尺度下的浅层特征信息进行学习训练，增加网络结构对图像尺度的适应性[16]，具体如图2所示。为保证输出特征与输入图像尺度一致，三种卷积核的中心点重合。

在上述的特征输出结果中，所有的特征尺度相同，则需要采用边界扩充技术使每次运行的三种卷积核的中心位置保持一致，具体如图3所示。然后以此方式进行卷积运算，并逐步扫描全图实现多尺度特征的提取。上述操作中，每个卷积核都能够得到与输出尺寸相同且包含不同尺度特征的映射图。

在本文中，三种尺寸的卷积核数量分别为12、32、20，则最终得到64幅尺度相同的特征图，将上述特征图并联作为下一层网络的输入。和DnCNN的卷积核提取模式相比，上述方式能够提取更为丰富的特征信息，从而有效提高浅层特征对不同尺度的适应性。

1.2.2跳跃连接网络的应用

获取浅层特征后，需要后续的网络层进行学习，计算得到更为复杂的特征，从而实现图像的去噪目的。DnCNN网络采用学习残差的方式，但是随着网络深度的增加网络的训练难度也逐渐加大，过多卷积层的堆积容易致使梯度消失，网络收敛性差[17-18]。为解决上述深度网络问题，本文引入跳跃连接方法，具体如图4所示。加入的跳跃连接网络可以将前面任意一层网络的激活输出传递给另外一层网络，加快网络的收敛速度，避免了反向传递过程中梯度消失问题，从而使网络更容易优化。

图4中，x表示网络的输入，F(x)表示经网络层的激活函数后的输出，即F(x)=δ1(x)，δ1表示前面网络层的激活函数，F(F(x))表示后一层网络的输出，即F(F(x))=δ2(δ1(x))，δ2表示后面网络层的激活函数。包含一个跳跃连接和几层深度网络的组成称之为一个残差单元块。

1.2.3损失函数及激活函数的优化

DnCNN中的均方误差损失函数是逐像素计算输入输出之间的差异，容易出现边缘纹理模糊的现象。针对上述问题，本文联合基于图像高级特征的感知损失函数作为改进的损失函数，将逐像素损失和感知损失同时作为训练目标进行网络训练，在具有较高去噪效果的前提下对图像的边缘纹理信息进行保护，则改进后的损失函数为：

(7)

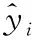
在实际应用中，通常采用随机梯度下降算法对上述函数进行优化，但是该算法在进行参数更新过程中，学习速度保持不变，对于算法效率的提升有限，因此本文采用自适应矩估计算法对误差函数进行优化。改进的优化算法是随机梯度下降算法的一种扩展形式，然后针对不同参数设计不同的自适应学习效率，从而有效解决深度学习网络中大数据参数优化的问题，参数数目少，效率高。

在DnCNN网络中，通常采用线性整流激活函数。然而，线性激活函数在负值时，数据的负轴信息全部归零，容易造成信息泄露和丢失[19]。因此，本文采用带泄露函数作为激活函数，有效改善上述不足，函数表达式如下：

(8)

式中：fi表示函数的输出；ci表示输入；α为泄漏系数，取值范围为[0,1]。两种激活函数如图5所示。

采用上述带泄漏激活函数作为权值初始化策略，能够以端到端的形式训练很深的网络。

1.3 改进后的卷积网络结构

改进后的深度网络结构如图6所示，在实际应用中，可以根据情况使用多个残差单元块。其中最小的单个残差单元块如图4所示，里面包含两个卷积层，批归一化及带泄露函数组成的激活函数，以及跳跃连接的输入和输出。由图6可知，整个网络在进行传递时忽略相同的主体，将权重主要作用于微小变化，从而解决网络退化、梯度值衰减消失的情况，改善输入图像和输出残差之间的映射关系。通过上述跳跃连接，使得深层梯度值直接传送至浅层网络层，杜绝了梯度衰减消失的隐患，从而使浅层网络得到有效训练。

由图6可知，得到网络输出的残差特征转化为图像f(x)后，去噪后的图像y可以表示为：

y=x-f(x)

(9)

式中：f(x)表示特征映射到图像的一种函数关系[20]。

2 仿真模拟

2.1 训练数据集

本文选用图像处理标准图集和部分无噪CT图像作为训练数据集，部分训练数据集如图7所示。

上述训练图集的图像特征丰富且多样，卷积网络训练范围广，训练模型适用性强。在实际应用中，为进一步提高和扩大深度网络的适用性，提升模型的泛化性，通常需要对上述测试集数据进行扩充[21]。由于高质量的CT图像通常数目较少，因此可以将少数高质量的CT图像进行分割、旋转等实现训练数据集扩充。以胸部CT图像为例，将其进行不同角度的旋转，从而有效扩大训练数据集，具体如图8所示。

2.2 参数设置

深度网络的第一层由3个尺寸卷积核组成，其中3×3、5×5、7×7三种尺寸大小的卷积核分别为12、32、20个。中间层统一使用64个3×3大小的卷积核，最后一个网络层使用灰度图的3×3大小的卷积核进行特征映射，训练步长为16，网络的初始学习率设置为10-4。

2.3 实验结果分析

为定量分析DnCNN算法、ID-CNN算法和本文算法的差异性，采用相同的参数，记录三种算法的损失函数以及去噪结果的峰值信噪比(PSRN)随网络训练次数的变化值，结果如图9所示，其中测试图像为含均值为0、方差为50高斯白噪的测试图像。

可以看出，在相同的损失函数误差值下，本文算法相对DnCNN、ID-CNN算法收敛性更好；同等的训练次数下，本文算法的去噪结果PSNR值更高。

为进一步验证本文方法的有效性，分别采用曲波变换算法、BM3D算法、DnCNN算法、ID-CNN算法和本文方法对测试图像进行去噪处理，并将五种方法的去噪结果进行对比，表1和表2分别展示了不同噪声情况下五种去噪结果的峰值信噪比和结构相似性(SSIM)数值。

表1 不同方法去噪结果的PSNR 单位：dB

表2 不同方法去噪结果的SSIM

由表1和表2可以看出，五种方法对于不同比例的噪声图像，其去噪结果均能取得较好的峰值信噪比和结构相似度。随着噪声比例的增加，五种方法去噪结果的峰值信噪比和结构相似度均有不同程度的下降，但是本文网络能保持在一个较高的数值范围，说明具有较好的去噪效果及图像质量提升能力。相对于噪声图像，曲波变换结果的PSNR值平均提升48%，SSIM值平均提升至0.833；BM3D结果的PSNR值平均提升53%，SSIM值平均提升至0.849；DnCNN结果的PSNR值平均提升54%，SSIM值平均提升至0.858；ID-CNN结果的PSNR值平均提升54.8%，SSIM值平均提升至0.864；本文方法结果的PSNR值平均提升56.3%，SSIM值平均提升至0.881。

然后将测试图像的图像结果进行展示，重点分析噪声标准差为10和50的去噪结果，结果如图10和图11所示。

由图10可知，五种方法均能去除图像的噪声，但是不同方法去噪效果不同。曲波变换的去噪结果相对较好，但是边缘/纹理细节相对模糊，BM3D的噪声残差中存在较多的边缘/纹理细节，说明对边缘/纹理等有效信号有所损伤。本文算法和DnCNN、ID-CNN算法结果最好，且去除的噪声残差中有效边缘信息及纹理信息较少，说明在低噪声的情况下，本文去噪方法和DnCNN、ID-CNN网络具有同等的去噪效果。然后再次分析含高比例噪声图像的去噪效果，具体如图11所示。

由图11可知，在高比例噪声情况下，曲波变换在去除噪声的同时容易损伤边缘/纹理等细节信息，使得去噪结果模糊，图像的轮廓不易识别。对于DnCNN算法和BM3D算法，其去噪结果对原始图像中纹理较弱的区域容易丢失细节，且去除的噪声残差中也包含较多的细节纹理信息，具体如图11(c)、(d)、(i)、(j)的椭圈区域；ID-CNN结果的噪声残差中连续性信息相对较少，但是弱反射区域图像质量相对较差，存在部分线性噪声，具体如图11(e)、(k)所示。而本文方法则能够较好地保持更多的有效细节，边缘轮廓更容易识别判断，具体如图11(f)、(l)所示。对图11(g)方框所示范围内的五种去噪结果进行放大显示，结果如图12所示。

由图12椭圆框区域可知，曲波变换结果较模糊，边缘/纹理细节信息很难识别，DnCNN和BM3D结果相对较好，图像相对清晰，但是图12(b)和图12(c)中的边缘/纹理细节区域图像质量依旧较差，要么不够清晰，要么依然存在部分噪声；ID-CNN算法中，边缘轮廓较为模糊，纹理细节不清晰；而本文的去噪结果相对DnCNN、BM3D和ID-CNN的去噪结果更清晰，能够保留更加丰富的纹理细节，“篮网”及“篮网”后面的“字母”纹理信息、下方的“广告板”边缘等信息更容易识别，说明本文方法在保留边缘及纹理细节方面具有更好的优势，能够得到更加清晰的图像结果。

然后采用四川某医院的大脑CT图像做进一步测试，五种方法的去噪结果及其各自的噪声残差如图13、图14所示。

由图13可知，五种方法去噪结果中，曲波变换细节信息模糊，BM3D算法、DnCNN算法、ID-CNN算法及本文算法均能有效抑制图像中的噪声，去噪结果均具有较好的视觉质量。五种结果的局部放大图中，BM3D算法、DnCNN算法和ID-CNN算法对部分纹理/边缘信息不能有效保护，造成了原始边缘/纹理细节信息的丢失。本文方法结果的边缘细节信息保护较好，去除结果和原始无噪图像更为接近，具有更好的图像质量，具体如图13(i)、(j)、(k)、(l)中的箭头所示。图14中，曲波变换的噪声残差中包含较多的细节信息，BM3D算法、DnCNN和ID-CNN算法的噪声残差中相对较少，但是依旧可以看见部分连续的边缘轮廓信息。而本文方法的噪声残差中，有效的边缘纹理信息最少，说明对边缘/纹理等细节信息保护最好，具体如图14中圆框中所示。

综合图13和图14可知，在医学CT图像的噪声去除过程中，本文方法具有较好的去噪效果及边缘纹理细节保护能力，图像边缘清楚，细节清晰，视觉效果好，图像质量高，所反映的人体组织轮廓及位置分布更容易识别，具有较好的图像处理推广应用效果。

3 结 语

本文基于多尺度特征提取的残差网络进行医学图像去噪，该方法基于原有DnCNN算法原理，改进其网络结构，对激活函数和损失函数进行优化，采用多尺度卷积核组合的特征提取层，提取不同尺度特征，增加网络对不同尺度的适应性，添加跳跃连接，加快网络的收敛速度和精度。测试结果表明，改进的深度网络算法能够有效提升图像质量，改善图像视觉效果。然而因相关条件限制，本文方法依然存在更大的提升空间，需要在后期的工作中进一步改进和完善，根据目前的成果，结论如下：

(1) 本文所用训练测试图集默认都是干净无噪图像，然而实际工作中很难拥有理想无噪的医学图像，因此如何提升训练图集的质量也是提升本文方法去噪结果的方法之一。(2) 实验模拟噪声均是基于高斯白噪的设想，但是医学图像成像原理及成像环境复杂，其医学图像含噪类型多样，测试结果难以严格匹配医学图像去噪的本质需求，因此后续工作需要进一步研究更匹配实际情况的深度模型，从而实现医学图像处理的最终目的。