基于蚁群算法的风电ADRC变桨控制器优化设计

贺耀庭 谢 源 李少朋 张 凯

(上海电机学院电气学院 上海 201306)

0 引 言

近年来，大型变速恒频风电机组的并网数量不断增加，大规模容量的风电场并网将严重考验电网运行的可靠性和稳定性[1]。当机组风速高于额定风速时，可通过改变叶片的迎风面积(改变风能利用系数)，即调节机组桨距角的大小，使机组的输出功率稳定在额定功率附近[2]。PID控制因其具有结构简单、稳定性较好等良好控制品质，从而在现代工业控制中仍占据主导地位。文献[3]提出了基于变增益的PID变桨控制，通过根据输出桨距角的大小，进而改变PI变桨控制器的增益，使系统的响应曲线变得更加光滑，增强了系统的稳定性和鲁棒性。文献[4]提出了一种基于加性分解原理的方法来优化PID控制器参数，将复杂的系统问题分解为线性时不变主系统的追踪和辅系统两个简单子问题，使机组能进一步平稳地输出其发电功率。文献[5]提出了多PID切换变桨控制，通过在分析风轮气动特性的基础上，对模型进行分段性建模，以设计适合于各风速区的多PID控制器。尽管以上方法相比于传统PID控制在控制效果上取得极大提高，但风力发电机组易受外部扰动较大、机组各部分之间非线性耦合能力强，加之所受风速的湍流特性随机性大，因此在机组变桨控制系统方面，以上改进都难以满足现阶段的控制需求。

为解决精确建模这一瓶颈，韩京清[6]在分析传统PID控制理论局限性的基础上，结合现代控制理论，提出了“自抗扰控制”—(Active Disturbance Rejection Control，ADRC)，已广泛应用于机器人、飞行器和锅炉控制等实际工程领域[7-9]。但ADRC控制器参数较多、难整定等问题，使得其实际推广应用受到限制。随着现代智能控制算法的发展，诸多算法已用于整定ADRC控制器参数，如文献[10]提出一种基于多目标飞蛾优化算法的自抗扰参数整定，文献[11]提出了一种基于思维进化算法整定ADRC参数，但以上优化算法皆易陷入局部最优，收敛速度较慢。

因此，本文提出一种基于蚁群算法(Ant Colony Algorithm, ACA)的优化自抗扰控制器方法，并将其应用于风电机组的变桨控制系统中，形成ACA-ADRC控制方法。仿真表明，将蚁群算法应用在控制器参数优化过程中，不仅算法收敛速度快，而且也提高了变桨距控制系统的抗扰能力和控制精度，使得系统的鲁棒性更强，发电质量更高。

1 系统建模

风力发电机组中的风轮模型作为一种机械能量转化装置，由空气动力学分析(叶素理论)可知，其在自然风中吸收的风功率和风力机转矩为：

(1)

(2)

式中：Tw为风力机转矩；ρ为空气密度；R为叶片半径；v为风速；λ为叶尖速比；θ为叶片桨距角；ω为风力机转速；Cp(λ,θ)为风能利用系数。

式(2)中，风能利用系数CP(λ,θ)代表风力机吸收风能的效率，是关于桨距角θ和叶尖速比λ的非线性函数：

(3)

其特性曲线如图1所示。

当风速高于额定风速时，若不对风轮转速做出迅速有效的调节，桨叶片过快的频繁动作以及输出功率的高波动将会影响发电质量，并将有可能对风电设备造成损坏。因此，需要通过对叶片桨距角进行精确调整，有效控制风电机组输出功率，保证风电机组安全稳定运行。本文的主要研究目标是利用蚁群算法的优化特性对自抗扰控制器的参数进行自动整定，以改善变桨控制器的适应、调节能力。

2 自抗扰控制原理

自抗扰切换控制的思想基于PID控制难以“以误差消除误差”的特性，是在改进其固有缺陷的过程中而发展起来的一种新型控制技术。

自抗扰控制器主要由以下三部分构成：跟踪微分器(Tracking Differentiator,TD)、扩张状态观测器(Extended State Observer,ESO)和非线性误差反馈组合控制律(Nonlinear State Error Feedback,NLSEF)构成，其结构如图2所示(以二阶系统为例)。

(1) 跟踪微分器(TD)可以提取平滑、连续的输入信号及广义微分信号，实现指令的快速跟踪，防止出现超调量的现象，从而可进一步解决控制系统中超调与快速性之间的矛盾。

这里选取函数fst(·)设计跟踪微分器，其状态方程如下：

(4)

fst(·)函数的定义如下：

(5)

(2) 扩张状态观测器用于把影响系统输出的扰动扩张成新的状态变量，进行实时估计与补偿，其工作性能将直接影响自抗扰控制器的控制品质，实现其功能的状态方程如下：

(6)

式中：λ01、λ02、λ03为观测器系数，待优化参数；α1、α2、α3为幂函数指数值，可根据经验值整定。fal(e,a,d)函数表达式如下：

(7)

(3) 非线性误差反馈组合控制律。先将TD和ESO相互作用后所得的误差信号作为其输入，经过非线性组合控制策略后，可得到控制量uo。

(8)

式中：k1、k2为观测器系数，待优化参数；α4、α5为幂函数指数值。

3 控制器设计

3.1 自抗扰变桨控制器的设计

选取永磁同步型风电机组为例，将其风力机模型线性化，并取风力发电系统在额定风速以上运行时的一个平衡点A，对应的参数为Tro、θO、ωo。在A点把函数Tr(ω,θ,v)按其二阶泰勒展开：

αΔω+ξΔθ+γΔv+h

(9)

式中：h为展开高次项。

定义发电机的电磁转矩为定值：Tr(ωo,θO,v)=Tro=Te，变桨距执行机构的动态特性为：

(10)

风机的动态方程为：

(11)

以Δω为控制器输入，结合式(11)可推导出式(12)。

Tro+αΔω+ξΔθ+γΔv+h-Te

(12)

因此有：

(13)

取估计值bo=β/Jτ,其余为扰动分量d，从而设计了如式(14)所示的二阶微分自抗扰变桨控制器。

(14)

由式(14)的推导结果可知，其可全面地反映风电变桨距控制系统的数学特性，结合式(1)和式(3)就可完成对变桨距ADRC控制器的设计。在二阶ADRC控制器中，可令Y=Δωr、u=Δθr，其系统结构控制如图3所示。通过蚁群优化算法整定ADRC控制器中λ01、λ02、λ03、k1和k2参数即可实现对风电变桨距控制系统调节，使风电机组的输出功率始终快速在额定功率附近。

3.2 基于ACA的ADRC控制器参数优化

蚁群算法作为模拟自然界中群体蚂蚁集体觅食行为而兴起的一种新型仿生智能优化算法，具有较强鲁棒性、并行分布式计算和收敛速度较快等优点，已由从最初应用于解决旅行商路线问题发展到VRP、PSP、图像处理及参数优化等领域中[12]。

1) 数学模型。

蚂蚁在觅食过程中，在某一条选择的路径上会释放一种类似于“信息素”的化学物质，当这条路径上的化学物质浓度高于其他路径时，就会有越来越多蚂蚁在之后的觅食过程中选择此路径。因此这种正反馈机制算法的数学模型主要由“路径节点选择”和“信息素更新”组成。

(1) 路径节点选择：路径的选择取决于信息素浓度的大小，定义蚂蚁k在t时刻从节点i到节点j的转移概率为：

(15)

式中：α为信息素启发因子；β为路径启发式信息；τij(t)为节点i到j的信息素浓度；τik(t)为节点i的信息素浓度；ηij(t)为t时刻支路(i,j)上的能见度值。

(16)

(2) 信息素的更新：当所有蚂蚁遍历所有节点后，即完成一次迭代，此时就要对路径和节点上的信息素进行更新，所以信息素的更新是一种动态性质的更新，更新方式如下：

τij(t+1)=(1-ε)τij(t)+Δτij

(17)

(18)

(19)

2) 算法的实现步骤。

(1) 定义蚁群数量m、最大迭代次数n、节点以及初始化算法参数。

(2) 将m个蚂蚁置于各自的初始化领域，并根据式(15)计算各节点转移概率P。

(3) 计算蚁群完成一次迭代后的目标函数评价值，并记录ADRC控制器的当前最优解。

(4) 按照式(17)-式(19)进行信息素的更新，增加一次迭代次数，判断是否达到最大迭代次数条件，若已满足，则记录ADRC优化参数，退出运行；否则转到步骤(2)循环运行直至达到迭代要求。

蚁群优化ADRC控制器参数的步骤如图4所示。

3) 优化参数的转化。

在系统模型已确定的情况下，需由蚁群算法对变桨ADRC控制器中的5个参数k1、k2、λ01、λ02和λ03进行在线整定。根据预先设定好的寻优参数的范围，每个参数由5位有效数字的序列组成，具体数位应根据所设寻优参数范围而定；待优化参数之间是相互独立的，且每一位数值都是在-9～0或者0～9之间，因此每个参数的搜索范围为-999.999～0或者0～999.999。这样，一组优化参数{k1,k2,λ01,λ02,λ03}就可由一串25位的数字序列在25×18的网格中表示。

在优化前需根据各寻优参数的上下限范围在xOy坐标系中对节点进行初始化，其中横坐标x1-x5、x6-x10、x11-x15、x16-x20、x21-x25分别为k1、k2、λ01、λ02和λ03的数位，具体数值可由式(20)计算得出。当种群在满足迭代要求时，最优路径优化节点图path(y1,g,y2,g,…，ym,g,)，g≤n，如图5所示。

(20)

式中：xi(i=1,2,…,25)代表数字序列第i位数值。结合图5中的数字序列(-3444218116)/(261908031842058)可计算出k1、k2的值为-34.442、-18.116，λ01、λ02、λ03的值为261.90、803.18、4 205.80。

4) 目标函数的选取。

本文选用系统额定功率值与系统实际输出值的累计误差之和作为蚁群优化算法的目标函数，如式(21)所示；同时在考虑系统模型的前提下，建立如式(22)的性能评价函数。迭代优化过程如图6所示，能全面、准确反映蚁群算法对优化ADRC控制器参数的效果。

(21)

J=1/fitness(t)

(22)

式中：t为系统仿真时间；P(t)为系统输出功率；Pref为额定功率。

显然，基于蚁群算法优化的ADRC变桨控制器在第5次迭代寻优后，最优适应度函数值已基本达到最小，表明蚁群优化算法具有收敛速度快、优化效果极佳等的特点。

4 仿真研究与分析

本文在MATLAB/Simuink仿真环境下对ACA-ADRC变桨控制器的可行性进行仿真认证，模拟阶跃风、渐变风和湍流风三种风况条件下传统PID变桨控制器和ACA-ADRC变桨控制器对变桨系统的控制效果。PID变桨控制器的参数同样可由蚁群算法进行优化，参数整定值Kp=5.683 4、KI=2.168 4、KD=3.520 9,具体过程见参考文献[13]。同时为保证ACA-ADRC算法的收敛性，待优化参数的下限为[-40，-20，0，500，2 000]，上限为[-10，0，300，4 000，8 000]；算法其他参数设置为m=20、n=20、α=β=1、ρ=0.8。机组选取WC2000-99型的风力发电机组，主要参数如表1所示。

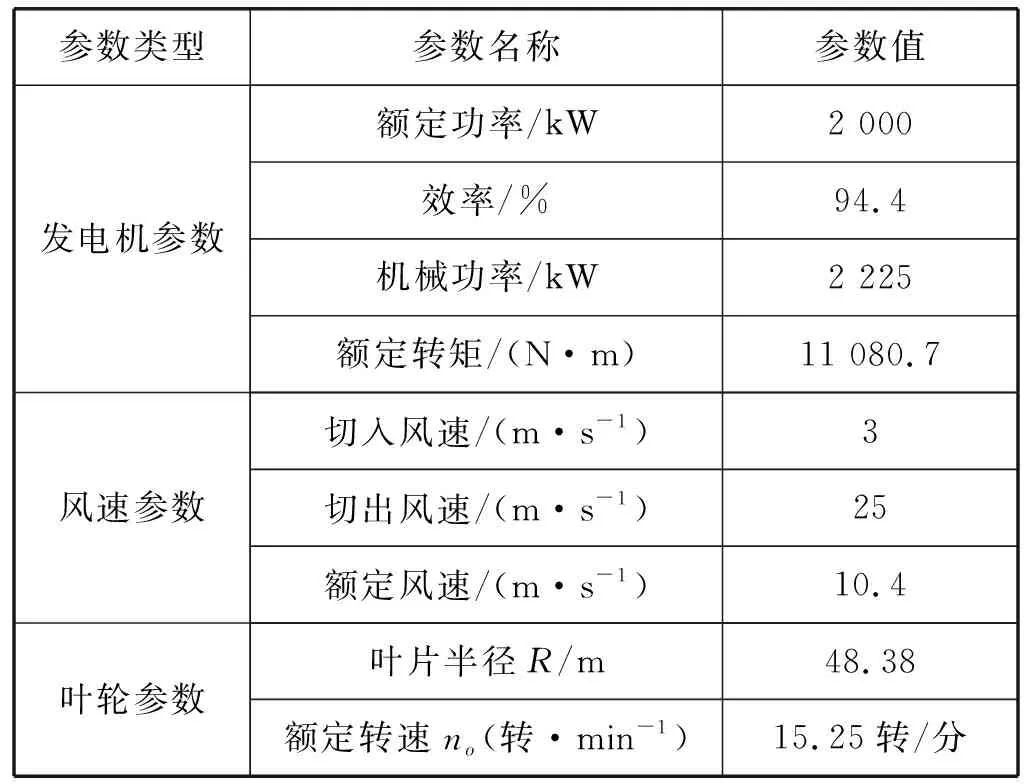
表1 机组主要参数表

对于风力发电机组而言，影响其发电质量的因素除系统的非线性、时变及强耦合的特点之外，另外一个至关重要的因素就是自然风速的随机性、波动性及不可控性。因此，依次以连续阶跃风、渐变风和湍流风为风力机输入风速，分别对ACA-ADRC变桨控制器和传统PID控制器进行仿真实验，得到每种风况条件下的机组性能曲线对比仿真图。

(1) 阶跃风工况：利用阶跃风工况对各控制器的性能进行仿真实验，其桨距角大小以及输出功率响应仿真结果对比如图7-图9所示。

在t=10 s和t=30 s时，风速由逐渐13 m/s突增至16 m/s，然后再增至18 m/s。特性变化曲线如图8和图9所示，此时ACA-ADRC算法变桨控制的桨距角响应超调量相比于PID控制有明显减少，分别由28.5%降至7.6%、13.8%降至3.2%，调整时间也明显缩短；与之相对应的是其功率波动也明显减少，表示基于蚁群算法优化的ADRC控制器能够快速、平稳地给定桨距角大小，提高控制效率及减少功率波动的优良特性，进一步提高系统的鲁棒性和静态性能。

(2) 阵风工况：阵风风况可反映风力机所受外部扰动的情况，阶跃突变规律从13 m/s增至15 m/s，持续时间大概为7 s，风况曲线如图10所示。

图11和图12为系统受到一个强干扰扰动信号时，即风速突变，桨距角控制信号和功率的调节过程。分析可知，在大扰动干扰的状态下，基于ACA-ADRC的变桨控制器对扰动具有估计和补偿作用，变桨距机构的调节幅度更宽，后期的动态稳定性更好；并且输出功率的超调量在扰动的状态下可由15.1%减少到3%，提高了发电质量。

(3) 湍流风工况：选取风速大小在11.5～14.5 m/s之间的随机信号模拟湍流风工况，风况曲线如图13所示。

以随机湍流风风况作为风力机的输入风速的结果如图14、图15所示。分析图14和图15后可得如表2所示的数据对比。显然，基于ACA-ADRC控制的桨距角能快速响应风速变化，使输出功率的波动误差由60.5%降为14.3%，稳定了系统的功率输出性能，提高了系统的控制精度和动态特性。

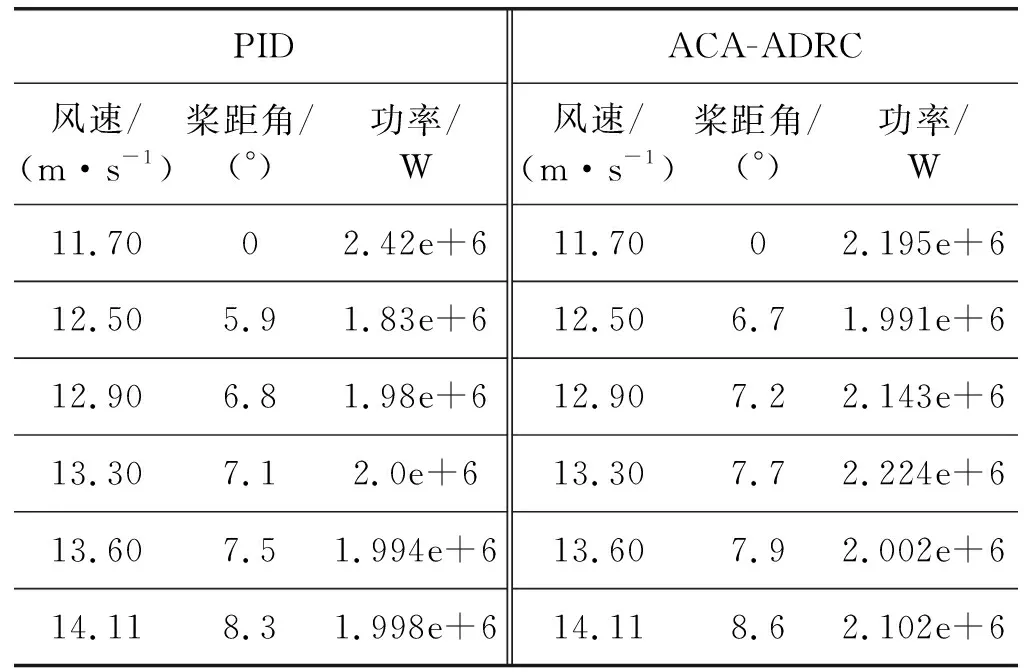
表2 数据对比分析表

5 结 语

本文针对传统PID变桨控制策略难以满足现阶段控制需求，提出一种基于蚁群优化算法的自抗扰控制，并设计了ACA-ADRC变桨控制器，仿真研究表明：

(1) 经蚁群算法优化的ADRC变桨控制器在阶跃风、渐变风、湍流风三种风况条件下，不仅系统响应时间更快、调节时间更短，而且拥有更好的鲁棒性，输出的电能质量更高；(2) ACA-ADRC控制器相比于传统PID变桨控制器，在系统遇到外界强干扰的情况下，有着更强的抗扰能力和控制精度，提高了系统的控制效率和稳定性。