考虑综合能源系统中不确定性因素的建模研究

陈培培，蒋雯佳，周瑜健，顾 馨，桂佩雯，丘世洁

（南京师范大学泰州学院 电力工程学院，江苏 泰州 225300）

随着全球气温变暖、能源资源短缺等问题的日益突出，我国于2020年9月提出的“双碳”（即碳达峰与碳中和）行动刻不容缓，在此目标下，电力系统势必会加快推动向清洁低碳的方向转型的工作[1]，而综合能源系统（Integrated Energy System，IES）无疑是最优选择。

IES是新一代的能源系统，与传统能源系统相比，其可以将新能源、电力和天然气等多种类型的能源进行耦合互补，不仅能够提高能源利用率，实现资源的优化配置，而且能够提供一种可持续发展的模式[2]。

新能源作为一种清洁高效的能源，将其接入电网具有明显的优势，但是新能源具有间歇性、波动性的特征，这也会对IES系统的稳定运行造成隐患。为了提高IES系统对新能源的消纳能力，提出了一种考虑新能源配额制的多园区IES优化调度的模型[3]，以此来保证系统的经济性；而基于电转气技术，提出了一种IES系统多目标优化调度模型[4]，考虑到低运行成本、低弃风成本与低环境污染3个目标，同时，也指出了在气—电互联系统运行时，天然气系统里的气负荷变化也会影响整个系统的经济性[4]。以上所提方法均可以很好地消纳新能源，但都没有考虑新能源引入IES系统中所带来的不确定性，在分析IES系统规划运行时，考虑了风电或光伏这一不确定性因素，从而提高了系统的可靠性[5-6]。

需求响应作为一种“削峰填谷”的重要措施，其需求侧负荷可以灵活地参与到电力系统运行中去。在IES系统中，系统呈现出多种能源耦合互补的趋势，需求响应的新概念“综合需求响应”也由此清晰。综合需求响应可分为基于价格型与基于激励型的，基于价格型的电负荷通过电价的调节变化引导用户自主做出用电行为的调整，起到合理分配电能的目的；而基于激励型的热负荷是采取经济补偿等措施鼓励用户在某时刻中断类似空调这类负荷，从而调度热负荷，达到节能减排的目的[7-9]。基于综合需求响应，建立了以运行成本最低和弃风成本最低的优化模型，达到降低运行成本，减少弃风的目的[7]；结合基于价格型和基于激励型2种综合需求响应，采用改进的二阶振荡粒子群算法对所提出IES调度模型进行求解，发现用户会从经济效益方面考虑转移部分用电，从而减少了系统的运行压力，也提高了系统的可靠性[9]；以工业园区IES系统为对象，在IES系统中加入综合需求响应，充分发挥了IES系统中电—热—气网的耦合优点，提高了系统运行的经济性与灵活性[10]；将传统的电力系统评价性指标引入到了IES中，建立气网的可靠性指标，同时加入综合需求响应贡献系数指标，以此对气电联合系统进行有效的可靠性评估[11]。

上述研究在IES系统中均没有考虑或者仅单一的考虑了某一类不确定性因素，没有将新能源、气负荷和综合需求响应等多重不确定性因素综合考虑分析[2-10]。而随着IES系统中各个能源的耦合程度的不断加深，其中所存在的多重不确定性因素不可忽视，如何处理这些不确定性因素，对其准确潮流分析、合理规划运行等研究具有关键作用。因此本文将从源、荷2方面针对IES中的主要不确定性因素进行分析并建立模型，以此提高IES运行的稳定性与可靠性。

1 源荷侧不确定性因素分析

IES系统虽然可以合理协调各个子系统的资源，但是该系统中却存在大量的不确定性因素，而这些不确定性因素的存在也极大地影响了IES系统运行的可靠性，因此分析这些不确定性因素的重要意义不言而喻。IES结构如图1所示。

从IES系统中的能源侧来看，一方面火力发电机组的出力存在不确定性，另一方面天然气站的出口压强也不易获取；如若接入大量的太阳能、风能等新能源，那么这些新能源所带来的波动性也势必会给系统造成更多的不确定性。

从IES系统中的负荷侧来看，负荷侧除了存在储能系统、可变负荷（比如电动汽车）这些不确定性因素，还存在气负荷，家庭用气负荷就与用电负荷一样，存在随机不确定性；当然最重要的一点是，需求响应可以起到“削峰填谷”的作用，如若负荷参与到需求响应中，那么就会大大增加IES系统运行的不确定性。其中IES系统中参与综合需求响应的负荷是由基于价格的电负荷和基于激励的热负荷构成，如图1所示。

图1 IES结构图

除了以上不确定性因素，还存在燃料价格变动、政策调整等影响因素，但在短期内这些影响因素可以暂不考虑。因此本文基于以上影响因素，并结合实际主要考虑针对能源侧中新能源、负荷侧中气负荷和综合需求响应这3方面的不确定性因素进行分析并建立模型，这些不确定性因素均存在一定的波动性。

2 不确定性因素模型

从古至今，不确定现象形式多变，学者们在分析大量的不确定现象的过程中，发现了这些不确定性信息表现出灰色性、模糊性、未确知性和随机性等方面的特征，而处理这些信息的方法则被称为不确定性数学[12-13]。不确定性因素建模是分析IES系统不确定性的基础，而针对影响IES系统稳定运行的不确定性因素，目前主要有2种方法处理，一是区间分析法，二是场景分析法。区间分析法是以区间来描述不确定性的数据，从而实现数据的存储与运算；场景分析法则可利用一些具有代表性的场景来表征不确定性因素的波动特征。

虽然这2种方法都能够很好地处理不确定性因素，但是考虑到后续若需进行IES系统的潮流分析，由于区间分析法采用区间变量，会导致其在加减迭代过程中不断增加，从而影响潮流计算结果的精确性；此外，上述不确定性因素具有一定概率分布特征，而场景法恰好能够根据其特征将随机模型转化成确定的场景模型。因此本文采用第二种方法，即场景分析法。

本文以K均值聚类的方法产生几种场景的方法为例，K均值聚类方法是通过判断待聚类点到中心点的距离长短来聚类的一种方法，其算法步骤如下。

步骤1：输入数据样本，确定聚类个数、若干聚类对象的聚类中心。

步骤2：计算每个聚类对象中聚类点到中心点的距离后，根据最小距离对相对应的聚类对象进行重新分类。

步骤3：重新计算各个聚类的平均值作为新聚类中心。

步骤4：重复步骤2和3，直至无改变，同时生成若干场景。

在医学生的本科学习过程中，对胃镜知识涉及的章节有限，且不作为常规教学内容，因此，研究生阶段学习胃镜的知识及操作可以帮助消化内科专业的研究生加深对消化系统疾病的认识并提高诊治能力。就目前我科室内镜室对研究生胃镜教学的现状，有以下几点思考。

IES系统中不确定性因素有新能源出力、气负荷、基于价格的电负荷和基于激励的热负荷，那么通过K均值聚类法生成c个场景的话，其概率分布特征如式（1）—（4）所示，则总概率分布集Xc等于各个场景概率集之积，总场景数Nc等于各个不确定性因素场景之积。

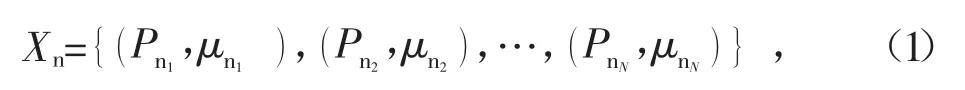
式中：Xn表示新能源出力概率分布集；Pn表示新能源出力；μn表示新能源出力负荷概率，且μn1+μn2+…+μnN=1。

式中：Xq表示气负荷概率分布集；Pq表示气负荷；μq表示气负荷概率，且μq1+μq2+…+μqN=1。

式中：Xd表示基于价格的电负荷概率分布集；Pd表示基于价格的电负荷；μd表示基于价格的电负荷负荷概率，且μd1+μd2+…+μdN=1。

式中：Xr表示基于激励的热负荷概率分布集；Pr表示基于激励的热负荷；μr表示基于激励的热负荷负荷概率，且μr1+μr2+…+μrN=1。

生成第c个场景μc的概率为

其中Σμc=1。

3 算例分析

本文采用6节点的系统，如图2所示，G表示发电机，L表示负荷。算例中假设新能源采用风电、气负荷、基于价格的电负荷和基于激励的热负荷数据[9]，并将其负荷扩大100倍。

图2 辅助检查工具

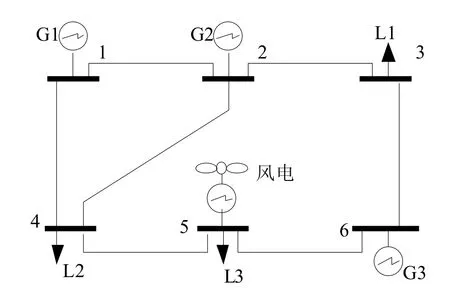
图2 6节点系统示意图

表1中列出了不同不确定性因素的每个场景的概率，可以发现所生成的每个场景概率不同，且每个不确定性因素的场景总概率均为1。

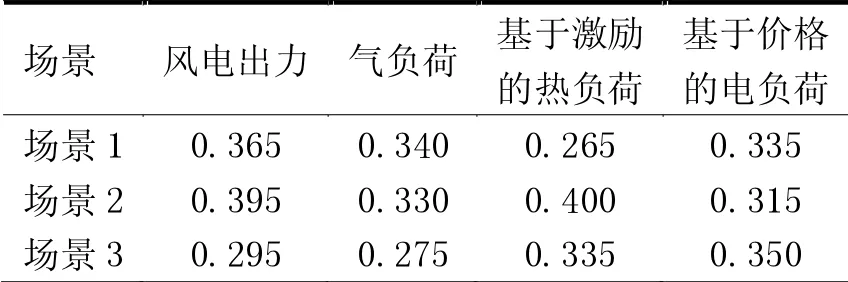
表1 不确定性因素的每个场景的概率

但是由于不确定性因素较多，其总场景数目Nc达到了81，数目较多，不便于后续研究。因此下面的算例引入等效负荷的概念，等效负荷等于用电负荷减去风电，而在本文中等效负荷则定义为基于价格的电负荷和基于激励的热负荷之和减去风电，如式（6）所示。如此，不确定性因素减少为2个。

等效负荷概率分布特征如式（7）所示

式中：Xe表示等效负荷概率分布集；Pe表示等效负荷；μe表示等效负荷负荷概率，且μe1+μe2+…+μeN=1。

式（5）更新为

根据K均值聚类方法生成等效负荷的3个场景如图4所示，每个场景的概率分别是0.385、0.325和0.29。总场景数目则大大减少，根据计算结果为9个。

从图3和图4中可以看出，风电具有反调峰特性，在用电负荷较低时，风电出力较多。另外，不难发现，等效负荷曲线走势受基于激励的热负荷的影响较大，2者曲线走势相似。

图3 不确定性因素的场景图

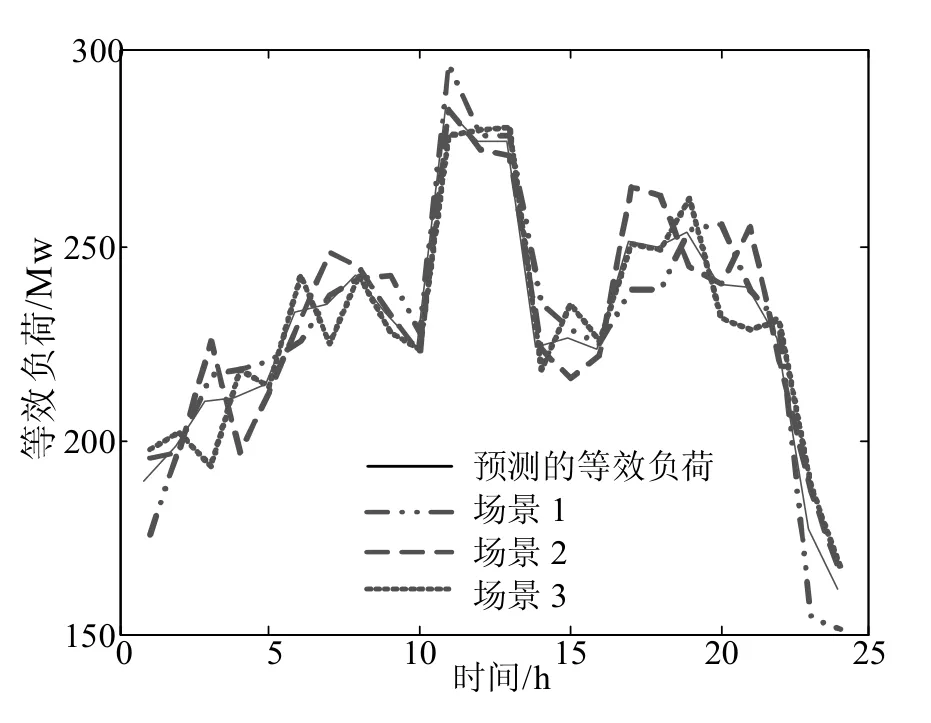
图4 等效负荷的场景图

进一步结合图3（b）与图4，根据式（8）计算9个场景的概率（保留3位小数），具体见表2，其总概率为1。

表2 总场景的概率

4 结束语

本文从综合能源系统中源荷侧2方面考虑，针对其中的不确定性因素进行了分析并建立模型。通过分析IES中的不确定性因素，确定对能源侧中的新能源与负荷侧中的气负荷、基于价格的电负荷和基于激励的热负荷这4种不确定性因素进行分析，并采用场景分析法，结合K均值聚类方法对其分别建立模型；为了进一步简化总场景的数目，引入了等效负荷的概念。IES系统中的不确定性因素模型的建立，为后续研究IES潮流分析、优化运行等内容奠定了基础，有利于进一步提高IES系统运行的稳定性与可靠性。