一种可选的电离层TEC 区域重构方法

车磊 欧明 陈奇东 蔡红涛 甄卫民 陈龙江 靳睿敏

（1.中国电波传播研究所,青岛 266107；2.西安电子科技大学，西安 710071；3.武汉大学电子信息学院，武汉 430072）

引言

作为表征电离层变化的一个重要特征参量，电离层总电子含量(total electron content,TEC)反映了众多电离层不同空间的变化特性[1-2].通过空间插值(spatial interpolation)的方法得到整个区域TEC 的预测值是TEC 区域重构常用的技术方法[3].由于电离层暴、太阳活动等自然现象的频发，电离层TEC 的非线性、非平稳变化可能存在波动和异常，影响无线电波的传播特性，不可避免地引起包括卫星导航、通讯、雷达和定位异常等问题[4]，因此，如何清晰地描述电离层TEC 的空间分布特征，准确地实现特定区域的电离层TEC 区域重构，完成电离层监测与预警，一直是相关领域研究的热点和难点问题[4-5].

当前，对于区域电离层TEC 区域重构主要通过空间插值的方法来估算一定区域范围内电离层TEC.这里提及的空间插值方法主要是基于已知观测站点获取的电离层TEC 真实值，通过插值的原理来估计其他位置站点的电离层TEC 预测值，其根本原理是通过基于构建的函数关系理论模型，综合已知监测站点的电离层TEC 空间位置关系以及空间相关性，从而估算其他任意点的电离层TEC[6].空间插值方法本质上追求构建尽可能符合原始观测数据的函数关系理论模型[7].

空间插值方法种类众多，应用也十分广泛.常用的插值方法包括反距离加权法、线性内插法、泰森多边形法、样条函数法、移动拟合法、趋势分析法、克里金插值法等.克里金空间插值方法(Kriging interpolation)适用于样本数据存在随机性和结构性特征的场景，应用于空气污染、降雨、环境监测等领域，并结合电离层TEC 空间分布的特殊性及相关性，得到了广泛应用[8].克里金空间插值方法又称空间自协方差最佳插值法[9]，基于区域化变量(regionalized variable)自身具有的随机性特征和结构性特征为基础，同时通过变异函数(variogram)对区域化变量进行空间描述，模拟地理现象空间分布的相关性和变异性，因此能够挖掘区域化变量的空间结构和空间变化规律[10].电离层TEC 正是具有这种随机性(不确定性)与结构性(相关性)双重特征的区域化变量，应用克里金空间插值实现对电离层TEC 区域重构，其实质在于通过已经位置点的电离层TEC 内插或外推的方式，对待估位置点电离层TEC 的取值进行无偏、最优估计[11].

诸多专家学者通过克里金空间插值方法实现了电离层TEC 区域重构.Stanislawska 等人改进了克里金空间插值方法，通过加入电离层空间距离的影响因素，实现对欧洲区域的电离层TEC 区域重构[12-13]；陈春等人根据foF2时间和空间相关性，通过克里金空间插值方法引入电离层空间距离、经度因子和纬度因子等参数实现了电离层TEC 区域重构[3]；刘瑞源等人提出了一种适用于中国地区电离层TEC 的短期预报方法，并定量分析了低纬站和边缘站对区域重构的精度误差影响[14]；然而通过克里金空间插值方法实现电离层TEC 区域重构过程中，区域重构的精度取决于模型对待估算点位和已知样本点位空间位置及其空间相关性这两者的反映程度[7].但随之带来的问题是，当克里金空间插值方法拟合变异函数时，传统理论变异函数模型面临函数曲线固定、空间细节变化无法反映以及模型选取人为主观等问题[15].

为解决上述问题，本文提出一种可选的TEC 区域重构方法，从电离层TEC 实际变化趋势出发，采用最小二乘支持向量机(least squares support vector machine,LS-SVM)拟合实验变异函数，实现电离层TEC 区域重构.为验证此方法的准确性，本文选用中国陆态网地基GNSS 台站某时刻三组不同时刻穿刺点垂直总电子含量(vertical TEC,VTEC)值作为实测数据，同时选用普通克里金空间插值方法中的指数理论变异函数模型、球状理论变异函数模型以及本文模型进行实验.结果表明，本文提供的电离层TEC区域重构方法计算的均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)均小于其他两种理论变异函数模型，插值精度最好，为电离层TEC 区域重构提供了一种可选的思路.

1 相关理论原理

1.1 克里金空间插值方法

克里金空间插值方法在有限的区域范围内对区域化变量进行无偏最优估计.区域化变量以自身具有的随机性特征和结构性特征为基础，对相关性和连续性等要素特点进行空间描述，模拟地理现象空间分布的相关性和变异性，因此能够挖掘区域化变量的空间结构和空间变化规律.同时借助变异函数，既能够描述其随机性变化过程，又能够反映区域化变量空间结构性变化过程[15].

变异函数 γ(x,h)定义为区域化变量z(x) 在x轴 方向上，z(x)在点位x和x+h处变量值之差的方差一半，如式(1)计算：

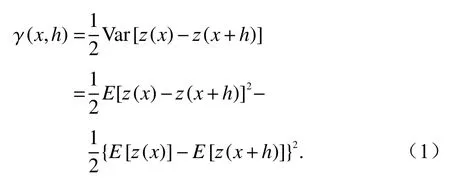
式中：Var[·]表 示方差；E[·]表示期望.

在二阶平稳假设的情况下，对任意样本点对的距离h有

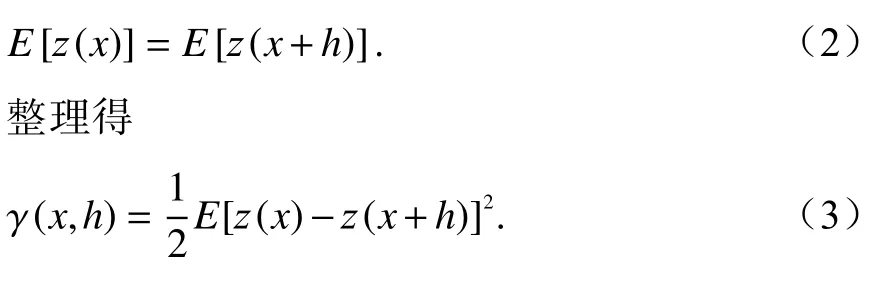
式(3)可理解为变异函数 γ(x,h)依赖于方向和距离两个变量变化，倘若变异函数仅仅依赖于距离变化时，则 γ(x,h)可以写为 γ(h)，同时称 γ(h)为 各向同性.此时，离散样本数据的实验变异函数可以通过式(4)所示：

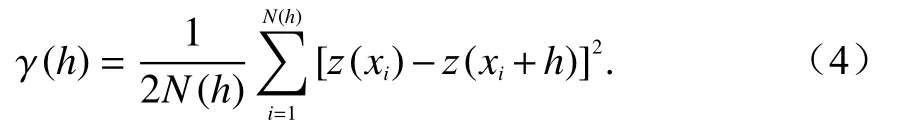
式中：h代表样本点对的空间距离；N(h)代表当样本点对距离为h时，所有样本点对的总数量；z(xi)和z(xi+h)分别表示z(x)在点位xi和点位xi+h处的实际观测值，即真实值.

克里金空间插值方法提供了包括线性模型、高斯模型、球状模型、指数模型等在内的几种常用理论变异函数模型[16].接下来以普通克里金空间插值方法为例，描述其实现的基本原理.

该方法实现空间估计主要满足两个基本条件：无偏性和估计方差最小，即：

求解得到如下方程组：

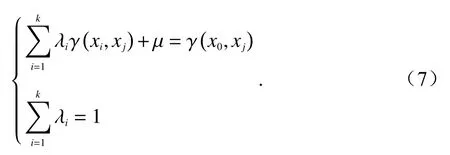
式中：λi为 空间权重系数，表示点位xi处的区域化变量z(xi)值对待估点位x0的贡献程度；j=1,...,k，k为监测站点的总个数；为点位xi与点位xj距离下的实验变异函数值；μ为拉格朗日乘子；为待估点位x0与点位xj距离下的实验变异函数值.

将式(7)用矩阵展开，得到：

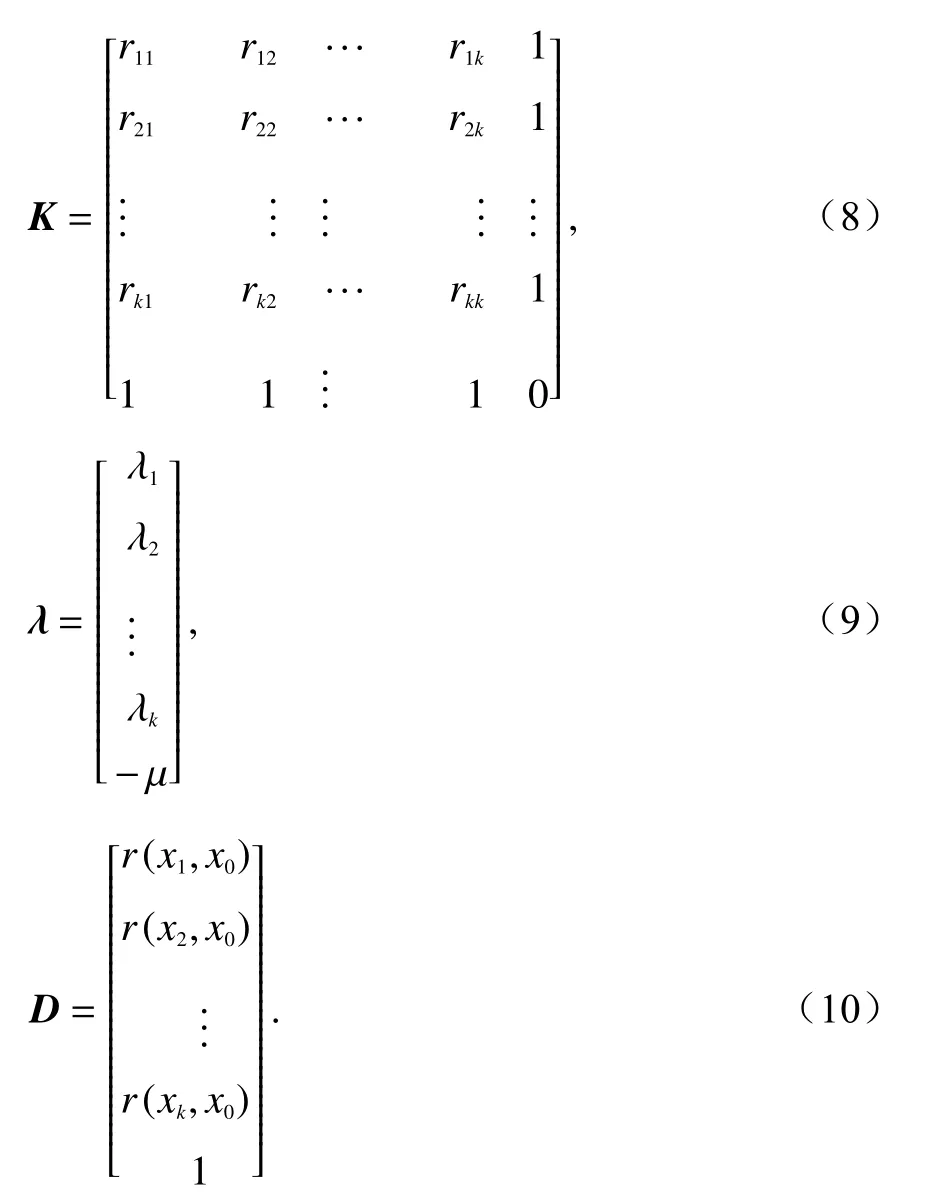
普通克里金空间插值方程为

解得

最终得到待估位置点x0处的区域化变量估计值z*(x0)：

式中：x1，...，xk为已知样本点位；z(x1)，...，z(xk)为对应样本点位的实际观测值.

综上所述，普通克里金空间插值方法基于无偏性和估计方差最小两个原则，在此基础上建立了含有约束条件的拉格朗日函数，插值结果的好坏完全取决于权重系数[8].通过约束条件和求极值问题解决待估位置点位区域化变量的无偏、最优估计[17].

1.2 LS-SVM

SVM 是由Vapnik 等人在20 世纪60 年代提出的一种有限样本机器学习理论，以统计学习理论为基础，SVM 模型不仅追求模型本身的泛化性能，且追求有限个样本条件下的最优解[18].SVM 模型构建过程中，以结构风险最小化为基础，主要用于处理小样本、高维数、非线性、局部最优解等问题.LS-SVM作为SVM 演变的一种类型，其原理是计算损失函数时，以平方和误差损失函数取代Vapnik 的ε 不敏感损失函数，同时构建等式约束条件[19-20]，计算原理如下：

给定N个样本数据集 {其中第m个 输入xm对应的输出值为ym，回 归函数f(x)的基本形式如式(14)所示：

式中：ω为权系数向量(列向量)；φ(x)为输入空间到特征空间的映射函数，即低维空间向高维空间转化的映射函数；b为常数项.

模型优化函数如式(15)所示：

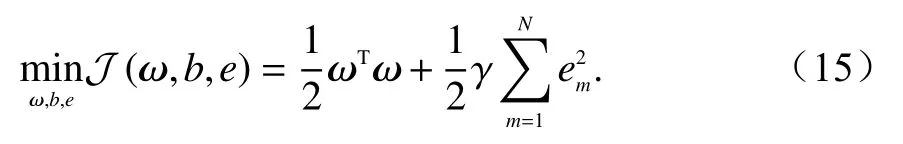
对应得到

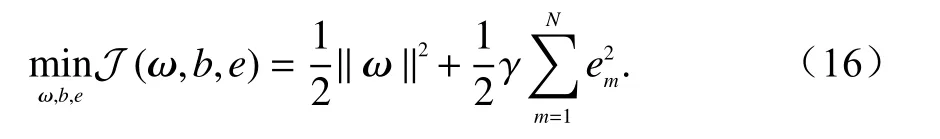
同时，上述公式也需满足以下等式约束条件：

综合上述条件，构建含有约束条件的拉格朗日函数，基于KKT(Karush-Kuhn-Tucker)条件，求解方程组，过程不再赘述.

最终回归函数模型f(x)如下：

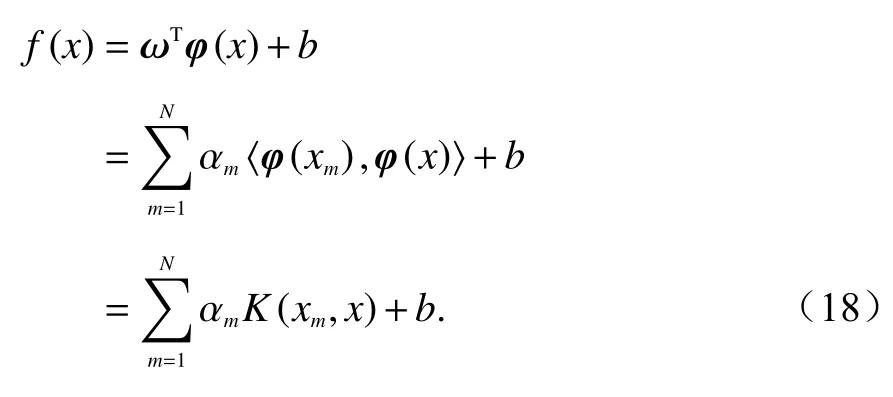
式中：αm表示拉格朗日乘子；K(xm,x)表示核函数.

2 计算流程

通过本文方法实现电离层TEC 区域重构方法，步骤如下：

步骤一：通过已知监测站点的地理坐标构建该区域网格化坐标点及范围.根据已知站点的地理坐标经度和纬度，以经度的最小值和最大值构建网格区域的长边，以纬度的最小值和最大值构建网格区域的宽边，完成区域网格化坐标点及范围的创建.

步骤二：借助离散变异函数式(4)，得到所有站点电离层TEC 样本点对的实验变异函数值，若实验变异函数值较多则进行分组操作，便于后续拟合实验变异函数.

步骤三：采用LS-SVM 拟合实验变异函数值，得到理论变异函数模型.通过LS-SVM 与克里金空间插值相结合，采用LS-SVM 拟合实验变异函数，能够更精确地刻画变异函数，反映电离层TEC 空间变化趋势.

步骤四：根据式(7)建立方程组求解权重系数 λi.构建含有约束条件的拉格朗日函数，通过步骤三得到理论变异函数模型及其他参数，求解权重系数 λi.

步骤五：根据式(13)计算待估位置点的电离层总电子含量z*(x0)，即实现了网格内所有待估位置点电离层总电子含量无偏、最优的估计.

3 实验分析

3.1 精度误差指标

为检验本文提出的电离层TEC 区域重构方法，借助RMSE 和MAE 两个精度误差指标[21].RMSE 反映的是灵敏度变化和可能存在的极值误差效应，MAE 反映的是总体精度误差.两个精度误差指标数值越小，表明电离层TEC 区域重构效果越好.RMSE和MAE 的定义如下：

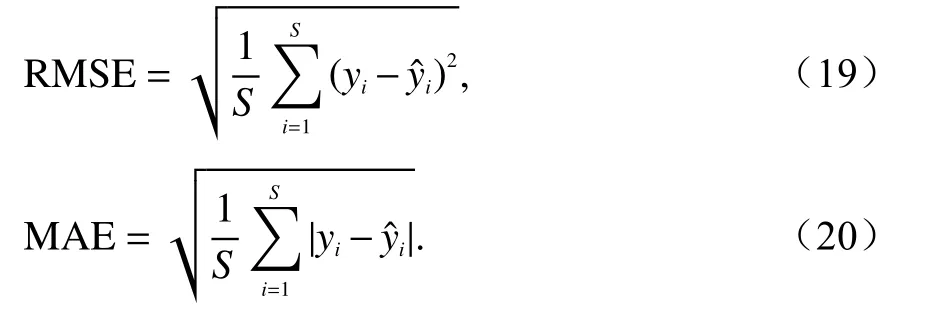
式中：S代表待估位置点的总个数；待估位置点的电离层TE C 真实值为yi；待估位置点的电离层TEC 估计值为

3.2 实验数据

以中国陆态网地基GNSS 台站三组不同时刻穿刺点观测值作为实验数据.采用文献[22]中方法对数据进行预处理得到斜向总电子含量(slant TEC,STEC)，再通过薄层模型(single layer model,SLM)映射函数[23]转化因子计算得到VTEC值，三组数据VTEC 分布如图1 所示.其中，(a)表示2017-09-05T14:00:00UT(第一组)穿刺点VTEC 空间分布，(b)表示2017-09-07T03:31:00UT(第二组)穿刺点VTEC 空间分布，(c)表示2017-09-10T06:18:30UT(第三组)穿刺点VTEC 空间分布.

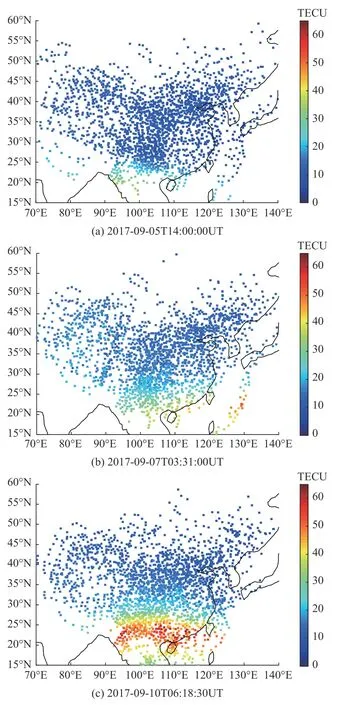
图1 不同时刻穿刺点VTEC 空间分布Fig.1 The schematic of puncture points VTEC spatial distribution at different times

同时为对比各组数据理论函数变异模型计算得到的MAE 和RMSE 两类评价指标误差，将不同时刻穿刺点VTEC 值划分为插值数据和测试数据.随机均匀抽取样本，通常插值数据占总样本数据的75%，测试数据占总样本数据25%，同时两者数据不重复，以满足计算过程的独立性[18].各组数据分类个数如表1 所示.

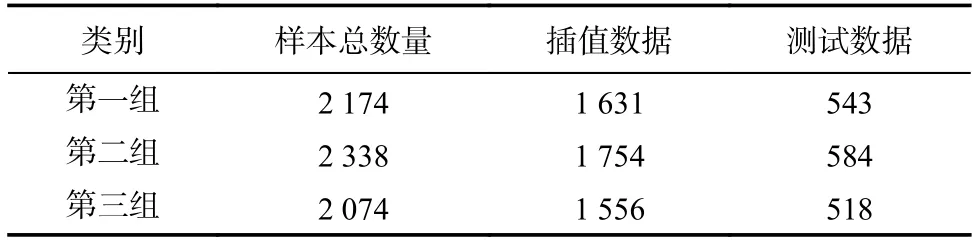
表1 三组数据样本类别及数量信息Tab.1 Three groups of data sample category and quantity information

区域重构范围为70～140°E、15～55°N，基本覆盖中国大陆区域，重构数据的网格空间分辨率为0.5°×0.5°.

3.3 实验结果

普通克里金空间插值方法中理论变异函数模型选用指数理论变异函数模型和球状理论变异函数模型，用于对比本文方法实现的电离层TEC 区域重构效果.图2 给出实验过程中实验变异函数的拟合曲线(以第二组数据为例).明显可以看出，LS-SVM 理论变异函数较好地拟合了所有实验变异函数值，整体拟合曲线符合电离层TEC 数据本身的空间变化特征，展现了数据本身的空间变化趋势.

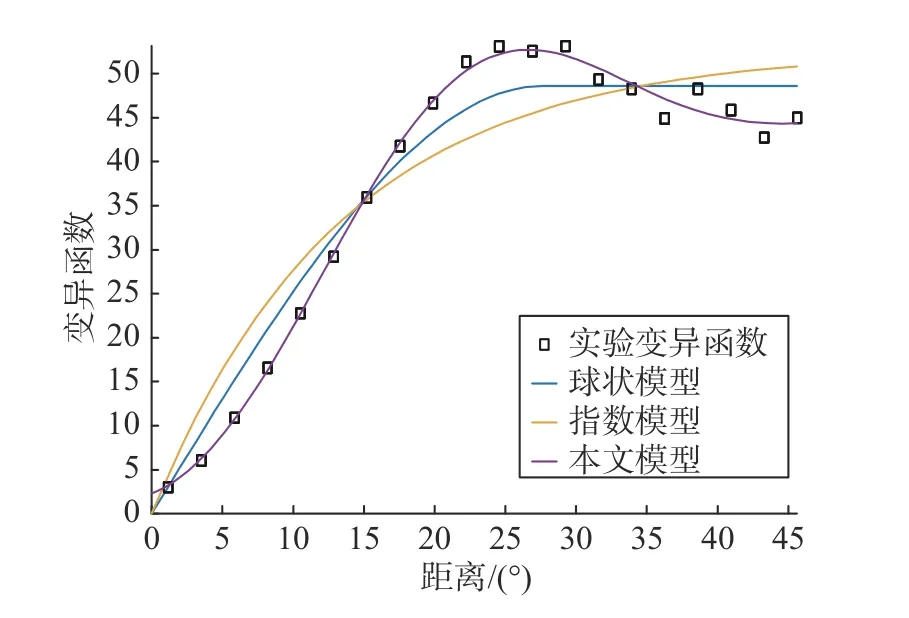
图2 变异函数拟合曲线Fig.2 Variogram fitting curve

图3、4 和5 分别为三组数据电离层TEC 区域重构效果.

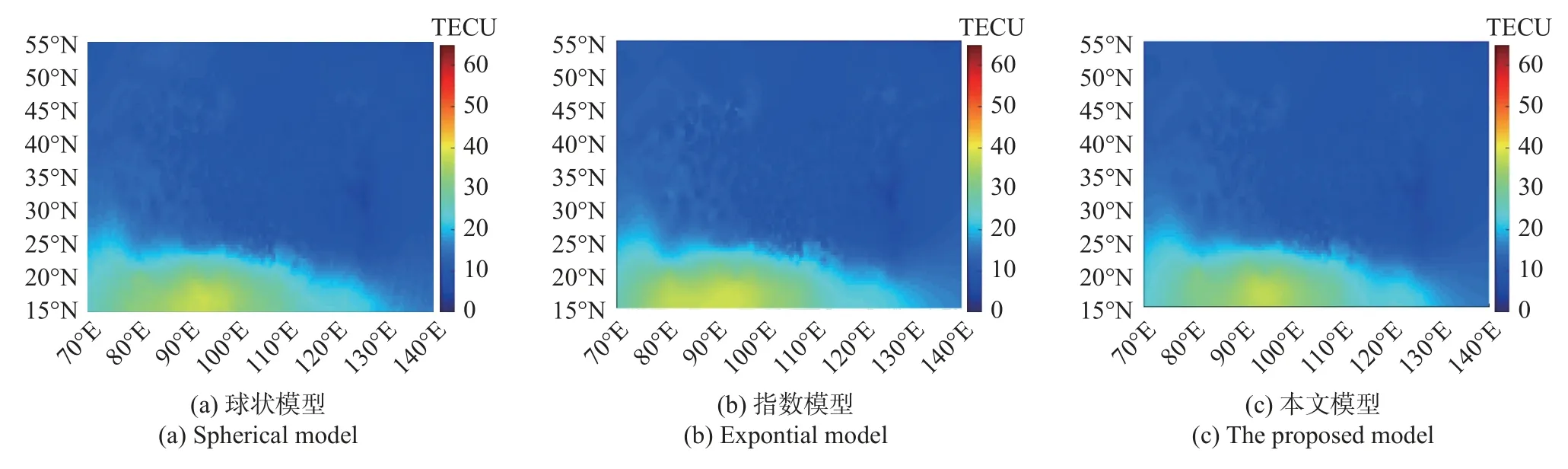
图3 2017-09-05T14:00:00UT 电离层TEC 区域重构效果Fig.3 The effect diagram of ionospheric TEC region reconstruction at 14:00:00UT on September 5,2017

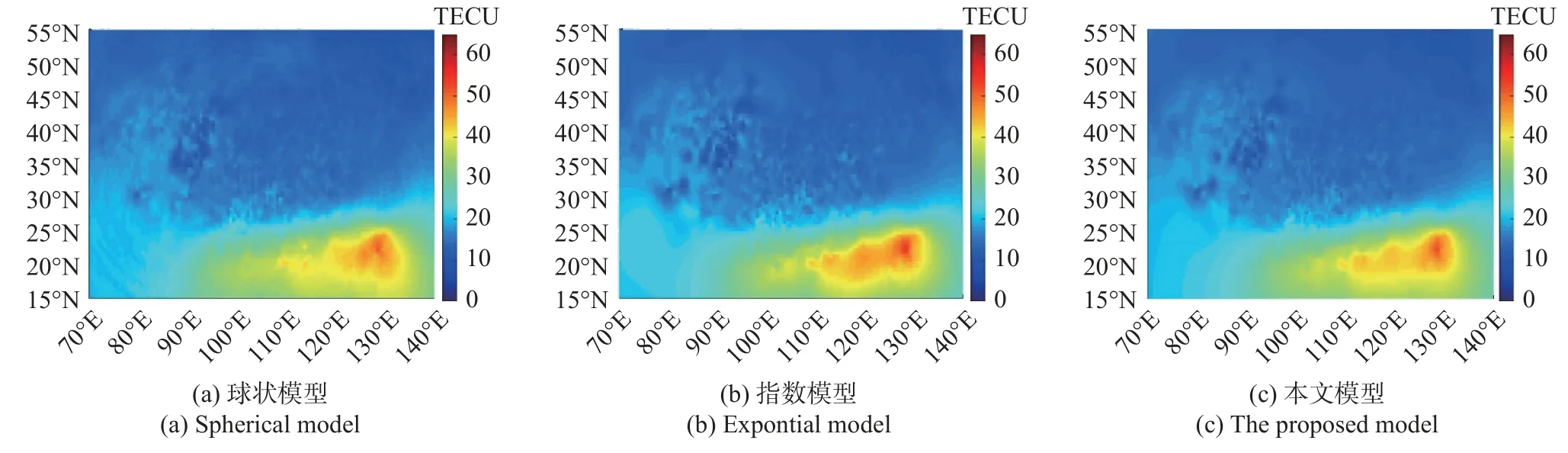
图4 2017-09-07T03:31:00UT 电离层TEC 区域重构效果Fig.4 The effect diagram of ionospheric TEC region reconstruction at 03:31:00UT on September 7,2017

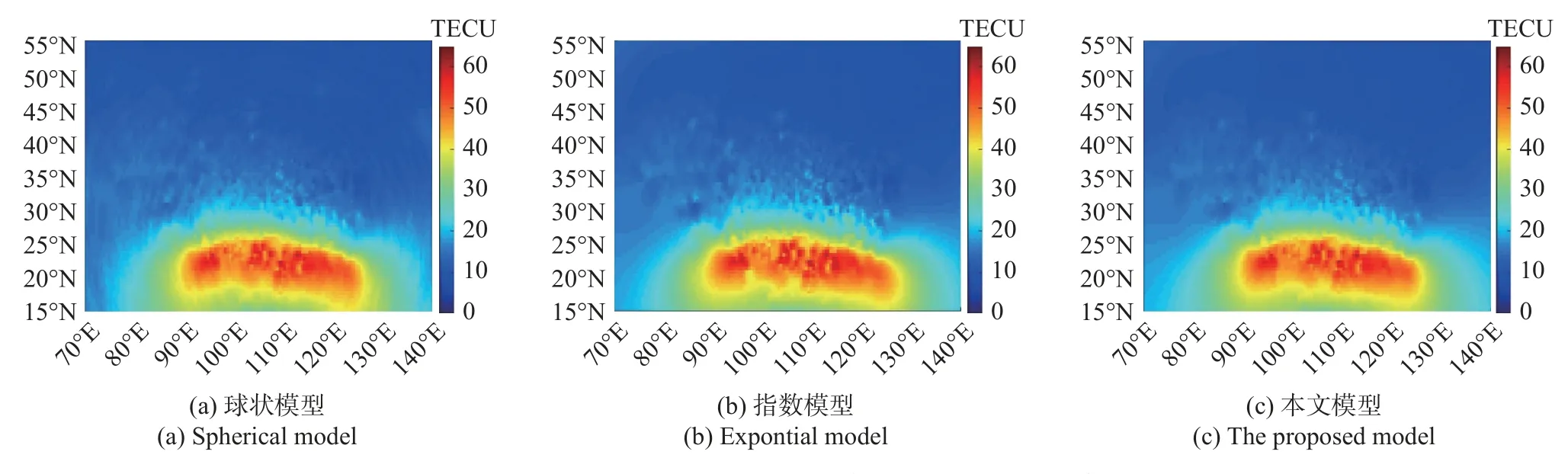
图5 2017-09-10T06:18:30UT 电离层TEC 区域重构效果Fig.5 The effect diagram of ionospheric TEC region reconstruction at 06:18:30UT on September 10,2017

从图3～5 可以看出，对比三种方法重构出来的电离层TEC 分布结果，LS-SVM 理论变异函数模型实现的区域重构效果大致符合通过克里金空间插值方法球状理论变异函数模型和指数理论变异函数模型重构的效果，三者空间变化趋势相近，空间变化呈现整体变化平缓、低纬地区偏高、高纬地区偏低的趋势，符合电离层TEC 空间分布特征.因此保守地认为，本文方法的确可以作为一种可选的电离层TEC区域重构方法.

从TEC 区域重构结果分析，TEC 值变化呈现从低纬地区向中高纬地区逐步锐减的趋势，本文选用的三组数据，包括夜间VTEC 和日间VTEC.第一组数据选用夜间VTEC，取值范围[0,35] TECU，变化平缓；第二组和第三组数据选用日间VTEC，取值范围[0,65] TECU，变化剧烈.三组实验数据整体时间变化趋势基本符合电离层TEC 的空间变化趋势，与文献[24]通过改进克里金空间插值方法给出的该区域电离层TEC 重构结果基本一致.

同时，为定量对比三种方法得到的区域重构结果精度误差，分别统计了不同理论变异函数模型下的RMSE 和MAE，如表2、表3 和表4 所示.

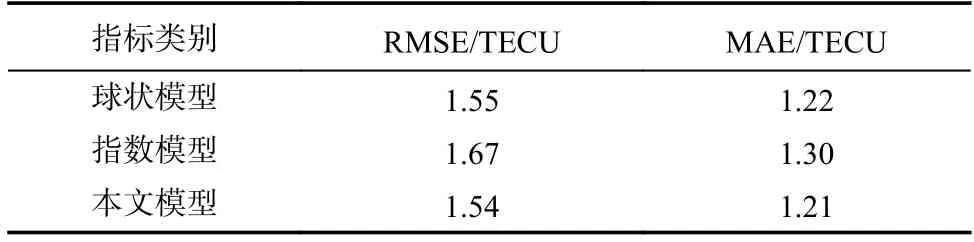
表2 第一组数据精度误差对比Tab.2 Accuracy error comparison (the first group)

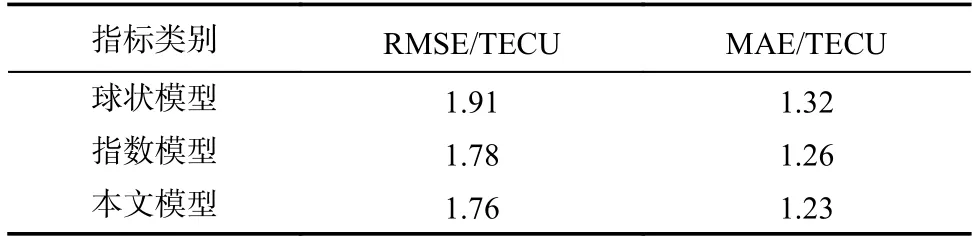
表3 第二组数据精度误差对比Tab.3 Accuracy error comparison (the second group)

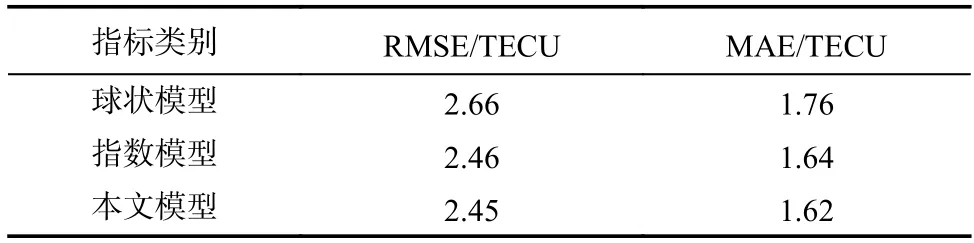
表4 第三组数据精度误差对比Tab.4 Accuracy error comparison (the third group)

表2～4 直观地显示出不同理论变异函数模型计算得到的电离层TEC 区域重构结果，传统克里金插值拟合模型中，指数理论变异函数模型误差小于球状理论变异函数模型；LS-SVM 理论变异函数模型RMSE 误差分别为1.54 TECU、1.76 TECU 和2.45 TECU，MAE 误差分别为1.21 TECU、1.23 TECU 和1.62 TECU.因此，这三种区域重构方法中，本文方法效果最好.同时，对比分析表2～4，三组实验数据精度误差存在差异性，作者分析认为，该差异性主要由数据本身的空间属性变化差异性引起.白天VETC值差异性明显，同时该研究区域中低纬地区处于电离层异常区域，梯度变化十分剧烈，引起的极值变化较多，因此精度误差偏大.相反地，夜间VETC 值变化则较为平缓且极值点较少，误差精度反而较低.

4 结论

电离层TEC 区域重构常采用克里金空间插值方法，但克里金空间插值方法拟合变异函数时，传统理论变异函数模型面临函数曲线固定、空间细节变化无法反映以及模型选取人为主观等问题，为解决诸如此类的问题，本文提出了一种可选的电离层TEC区域重构方法.这种方法通过结合电离层TEC 数据的空间变化特征，能够更精确地刻画变异函数，反映电离层TEC 数据在空间中的实际变化趋势，从而在一定程度上提高了电离层TEC 区域重构的精度.

需要与读者说明的是，本文提出的这种电离层TEC 区域重构方法主要基于两方面考虑：1)电离层TEC 数据本身是一种具有地理空间特性的区域化变量，在变化过程中与周围邻域的位置点及位置数据产生作用，体现为空间属性的相关性或相似性特征，因此适合采用克里金空间插值方法实现区域重构；2)电离层TEC 区域重构过程中，理论变异函数模型拟合实验变异函数离散点，如何实现更精确的拟合和更优良的泛化性能，是追求无偏性和最优解的目标.通过真实数据进行仿真验证，结果表明该方法在一定程度上可以提高插值精度，即提高电离层TEC 区域重构的准确性，为研究此领域的作者提供一种思路供大家参考借鉴.

但同时值得思考的是，实验过程中也存在一些需要后续继续研究的内容：不同样本数据即电离层TEC 数据计算得到的区域重构精度不尽相同，作者分析认为一方面是数据本身可能存在特殊性，另一方面LS-SVM 模型本身的泛化性能会根据数据的不同而存在差异性.后续研究不仅需要更多的数据参与实验验证，同时引入其他人工智能方法实现不同方法之间的对比提高.

致谢：本文GNSS 观测数据从中国大陆构造环境监测网络(Crustal Movement Observation Network of China，CMNOC)获取，作者在此表示感谢.本工作得到国家重点研发计划(2018YFF01013702 和2018 YFB0505100)的资助.