基于改进互耦系数估计算法的自适应波束形成

蒋凯 李良荣

（贵州大学大数据与信息工程学院,贵阳 550025）

引言

自适应波束形成技术概念最早由Van Atta 提出，至今已有50 年的历史.早期的自适应波束形成可以有效抑制干扰和噪声.第一个自适应波束形成器是1965 年Howells 提出的旁瓣相消器[1]，随后许多学者对旁瓣相消器进行了改进.郭庆华等提出了投影到信号子空间的改进方法[2]，但该方法在信噪比(signal to noise ratio,SNR)较低时其性能较差.1969 年Capon 提出的一种波束形成算法，使有用信号不失真通过的同时确保干扰信号和噪声的功率达到最小，该算法成为划时代的标志[3-4].此后一些稳健自适应波束形成算法被提出[5]：一类是基于特征空间的波束形成(eigen-subspace beamforming,ESB)算法，利用信号子空间特性但受限于信源数；另一类是基于协方差矩阵求逆(sampling matrix inverse,SMI)算法，该算法收敛速度快，但低SNR 时性能较差.

上述波束形成算法并不能很好地抵抗阵列互耦现象，近十年的研究中许多具有抗互耦效应的稳健自适应波束形成算法被提出.例如20 世纪90 年代著名的对角加载方法[6]，通过人为设置一个校准源来达到目的，但由于所用的校准信号源本身也会引入误差，导致算法有一定误差.2012 年，Yujie Gu 等提出了一种基于干扰与噪声协方差矩阵重构和导向矢量估计的波束形成算法[7]，但通过在剥离掉期望信号的角度范围内进行功率积分去除有用信号的分量来获得干扰和噪声的协方差矩阵，导致该算法无法利用所有阵元.Yang 等提出了协方差矩阵重构的抗阵列互耦算法[8-9]，该算法只需期望信号方向而不需要其他先验信息便可达到良好的抗互耦效果.吴晗提出了基于互耦系数估计的抗互耦算法[10]，先进行互耦系数估计，然后重构算法所需的干扰和噪声协方差矩阵.上述算法抗互耦性能较强，然而在低SNR 时性能衰退严重[11]，不能有效抑制噪声.

本文提出一种基于互耦系数估计的抗互耦算法(mutual coupling coefficient estimate based，MCCEB)，针对原抗互耦算法在低SNR 下互耦系数估计误差较大、波束形成性能相对下降的问题，对算法进行了改进.在输入SNR 低于设定门限的时候，仅用干扰信号的导向矢量来参与互耦系数估计；当SNR 高于设定的输入SNR 门限的时候，利用期望信号和干扰信号共同确定互耦系数.和原算法相比，改进算法降低了低SNR 下计算的复杂度，并通过改变期望信号在不同输入SNR 下是否参与估计互耦系数，提高了算法稳健性.

1 算法原理

1.1 算法描述

假设信号是平稳的，统计特性不随时间变化，定义输出信号的协方差矩阵[12]

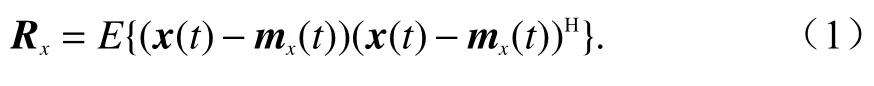
式中：mx(t)=E{x(t)}，且mx(t)=0.那么有

这里假设满足以下条件：

1)阵元个数M要大于可能接收到的空间信号的个数N；

2)对于不同的信号方向 θi(i=1,2,···,N)，信号的导向矢量是线性独立的；n(t)

3)噪声 是均值为零的高斯白噪声，

式中：σ2是噪声功率；I是单位矩阵.

信号向量的协方差矩阵为

由式(2)～(4)可得：

证明Rx是非奇异的，且Rx=是正定Hermitain 方阵[13]，利用酉变换实现对角化，相似对角阵由M个不同的正实数组成，与之对应的M个特征矢量是线性独立的.因此，Rx的特征分解可以写成

式中：Λ=diag(λ1,λ2,···,λM)，且

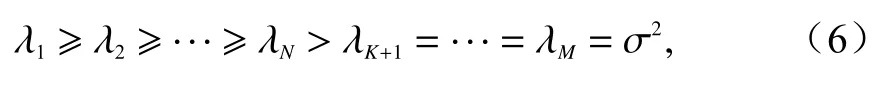
即前N个特征值与信号有关，数值大于 σ2，且特征值的大小与相应信号的功率有关，功率越大，对应的特征值也越大.信号的功率较大，N个信号对应特征值λ1,λ2,···,λN的特征向量e1,e2,···,eN组成信号子空间Us，以其值为对角线元素的对角阵为 Λs.噪声的功率较小，M-N个噪声对应小特征值 λN+1,λN+2,···,λM(数值均为 σ2)的特征向量e,e,...,e组成噪声子空间N+1N+2M Un，以其值为对角线元素的对角阵为 Λn.至此，可以将Rx写为

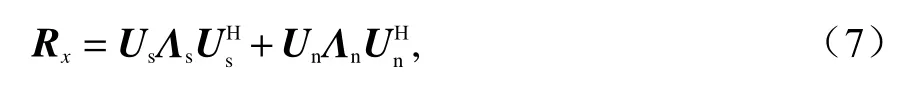
即将接收信号的矩阵分解为信号子空间和噪声子空间.

对于一个由M个阵元组成的阵元间距为d的均匀直线阵，设置忽略阵元互耦的门限为P个阵元间距，可知有互耦系数且参考处互耦系数是对称的，即

可见互耦矩阵是一个循环带状的Toeplitz 矩阵.

定义互耦向量

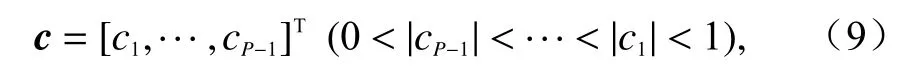
cj(j=1,2,3,···,P-1)表示互耦门限以内，与参考点的距离为j的阵元互耦系数.方便起见，设定一个阵元与其自身之间的互耦系数为1，则可以得到阵列的互耦矩阵如下：

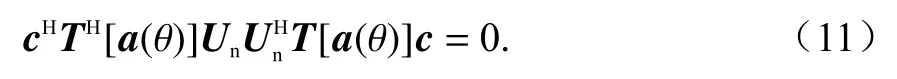
由此得到：

令

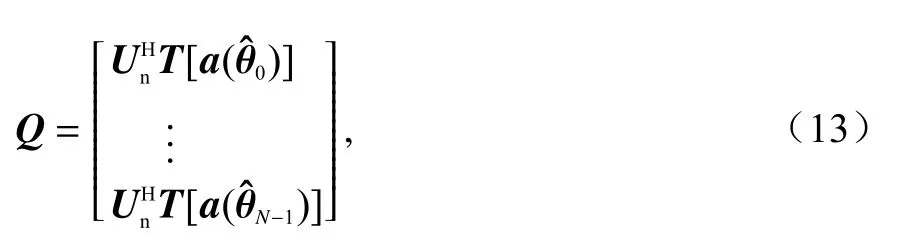
得到

式中，Q是N×((M-N)×P)阶的矩阵.用qi表示Q的第i列，则式(11)可以表示为

可以得到：

式中，(·)+表示对矩阵求伪逆.利用式(17)求得所有的非1 互耦系数，得到整个互耦矩阵.令估计得到的互耦矩阵为C′，原估计得到的导向矢量为ai，则可以得到修正后的导向矢量为

获得最新的导向矢量之后，进行Ri+n重构：

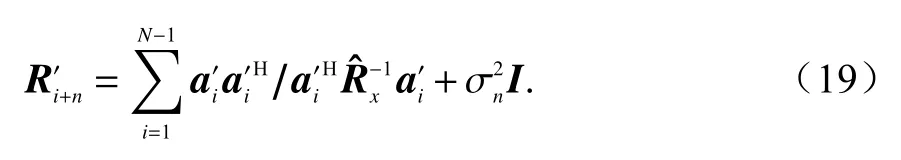
得到重构的干扰加噪声协方差矩阵之后，便可利用最小方差无失真响应(minimum variance distortionless response,MDVR)[14]波束形成器得到最佳权矢量.

1.2 原算法仿真

为便于比较，所有仿真都是基于阵元间距为半波长的16 元均匀线阵，入射信号为两个功率相等的干扰信号和一个期望信号，信号采样点数为200.将期望信号的角度区间设为 Θ=[θd-7°,θd+7°]，θd=0°，则干扰和噪声可能存在的区间为=[-90°,θd-7°)∪(θd+7°,90°].干扰信号设置来自± 30°，输入SNR 为0 dB，信干噪比 (signal to interference plus noise ratio,SINR)为30 dB，互耦向量中包含5 个值，即互耦门限为5，互耦向量元素根据互耦门限原理设定为[1，0.433 01-0.351j,0.261 8+0.217 6j,0.141 4-0.141 4j,0.080 8+0.080 8j]，图1 为基于互耦系数的抗互耦算法的归一化方向图.

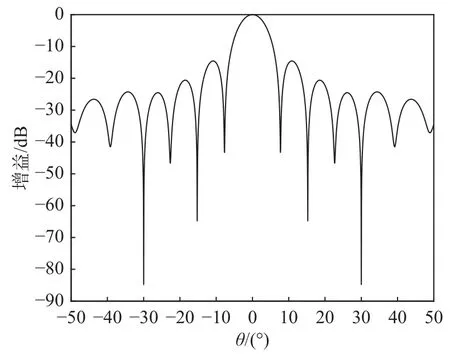
图1 基于互耦系数的抗互耦算法的归一化方向图Fig.1 Normalized pattern of anti-mutual coupling algorithm based on mutual coupling coefficient

从图1 可以看出，期望信号来向对应主瓣，干扰来向对应零点.基于极其准确的干扰信号方向估计的前提下，该算法具有一定的抗互耦性能，但当干扰信号的来波方向有较大误差时，对互耦矩阵的估计也相应地产生较大的误差，波束形成的方向图和输出SINR 随输入SNR 的变化曲线也将偏离标准值.

2 改进算法

2.1 原算法存在的问题

在对上述算法进行研究后，可以发现在DOA 估计误差准确或误差极小时，该算法具有近乎完美的表现.但当输入SNR 很小时，波束形成器的性能偏离理想曲线，即输出SINR 会偏离最优波束形成输出SINR.设置输入SNR 为-10 dB，仿真得出的输出归一化方向图如图2 所示.可以看出，在低SNR 条件下，相比图1，在干扰信号的来波方向无法形成较深的零陷，说明原算法在低SNR 时抗干扰性能较差，其波束形成器性能有所下降.针对这一现象将分析误差产生的原因并作出对原算法的改进.

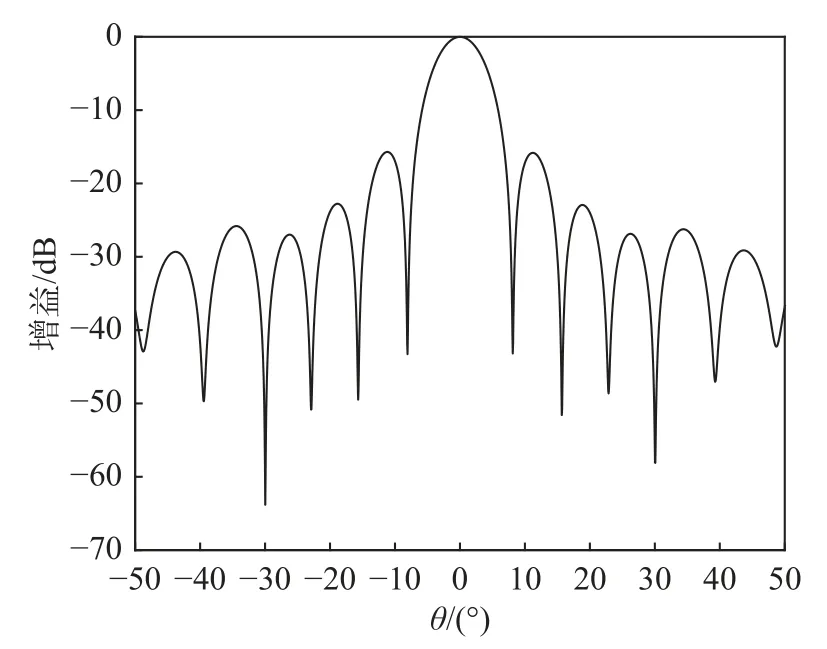
图2 低输入SNR 时波束形成输出归一化方向图Fig.2 Normalized pattern of beamforming under low input SNR

2.2 改进算法

互耦条件下自适应波束形成器的接收数据为

将C乘在矩阵A左侧即为接收信号，互耦所带来的误差全部作用在导向矢量上.

真实的导向矢量为

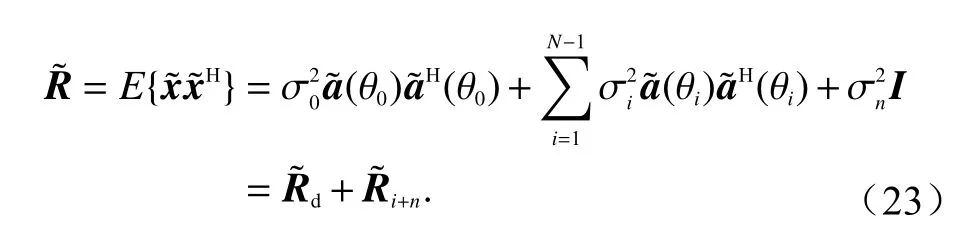
式中，期望信号

当互耦系数估计存在较大误差时，相应算法性能会下降.图3 为不同输入SNR 下100 次仿真平均值计算出的互耦系数均方误差(mean square error,MSE)的幅度和相位.可以看出，输入SNR 较小时，互耦系数估计具有较大的误差；SNR 较高时达到10 dB 后，互耦系数的估计误差逐渐减小至接近理想情况.因此可设定10 dB 为输入SNR 的一个门限，超过此值后可认为估计出的互耦系数没有误差.

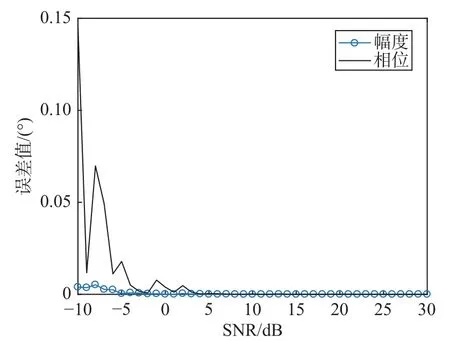
图3 互耦系数MSE 随输入SNR 变化Fig.3 Curve of MSE of mutual coupling coefficient with input SNR

从式(11)可以看出信号与噪声两子空间正交原理是互耦系数估计过程的主要依据.式(13)中为提高互耦系数估计的准确性，互耦系数估计过程中使用的是包括期望信号在内的所有信号，当数据协方差中含有较强期望信号时，互耦估计较为有效，期望信号与噪声的正交性将减弱，相关性增强，说明期望信号和噪声之间不是严格正交，而存在更高的相关性.将期望信号式(24)考虑进式(13)将会增大互耦系数的估计误差.因此在小于门限值时应忽略期望信号，而大于门限值时则保留期望信号，这是改进算法的依据.依据互耦系数MSE 得出10 dB 为本算法门限.

由图3 可以看到，在输入SNR 逐渐增加至门限10 dB 时，认为估计互耦系数已经是最优情况.因此当输入SNR＜10 dB 时，将式(13)改为

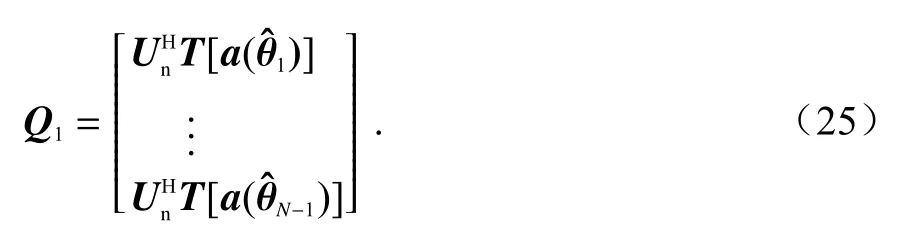
即在小输入SNR 条件下，舍弃式(24)中期望信号所对应的部分；当输入SNR ≥10 dB 时，仍采用式(13)Q矩阵形式：

从而降低了低SNR 情况下互耦系数的估计误差，提高了相应波束形成器的性能.

2.3 改进算法性能对比

仿真条件设置为：输入端SNR 为-10 dB，SINR为30 dB，期望信号入射方向为0°；空间中存在2 个干扰，干扰信号方向设为[-30°,30°]，信号采样点数为200 点；互耦向量中含有5 个值，互耦系数设置为[1,0.433 01-0.351j,0.261 8+0.217 6j,0.141 4-0.141 4j,0.080 8+0.080 8j].

将传统的ESB 算法、SMI 算法、干扰加噪声协方差矩阵重构(interference-plus-noise covariance matrix,INCM)[15]方法、改进前MCCEB 算法与改进算法进行对比，几种算法波束形成器的方向图如图4 所示.可以看出：改进算法主瓣对准真实的期望来波方向，在干扰信号来波方向形成较深零陷；SMI 算法主瓣并没有对准期望信号来波方向，也没在干扰信号来波方向形成零陷；ESB 算法主瓣对准了期望信号来波方向，但在多个干扰信号方向形成零陷；INCM 算法在干扰方向上没有形成零陷；原MCCEB 算法在低SNR 时没有形成较深的零陷.因此在低SNR 条件下改进算法性能优于其他对比算法.

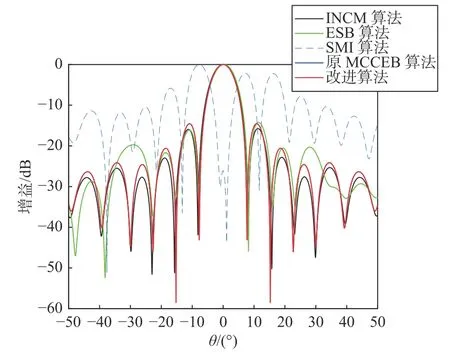
图4 几种算法在互耦情况下的方向图对比Fig.4 Direction diagram comparison of various algorithms in the case of mutual coupling

同样仿真条件下比较几种算法输入SNR 对输出SINR 的影响，图5 所示为几种算法在互耦情况下的输出SINR 曲线对比.可以看出：改进算法在低SNR 时输出SINR 性能优越，与最优(Optimal)算法输出SINR 重合，同时随输入SNR 增大而增大；SMI 和ESB 算法输出SINR 随输入SNR 的变化较为混乱，且与Optimal 算法输出SINR 相距较远；INCM 算法输出SINR 随输入SNR 的增大而增大，但仍略低于Optimal 算法输出SINR；原MCCEB 算法与Optimal 算法输出SINR 几乎重合，但在低SNR 时仍低于Optimal 算法输出SINR.综上所述，本文算法性能优于其他几种算法.

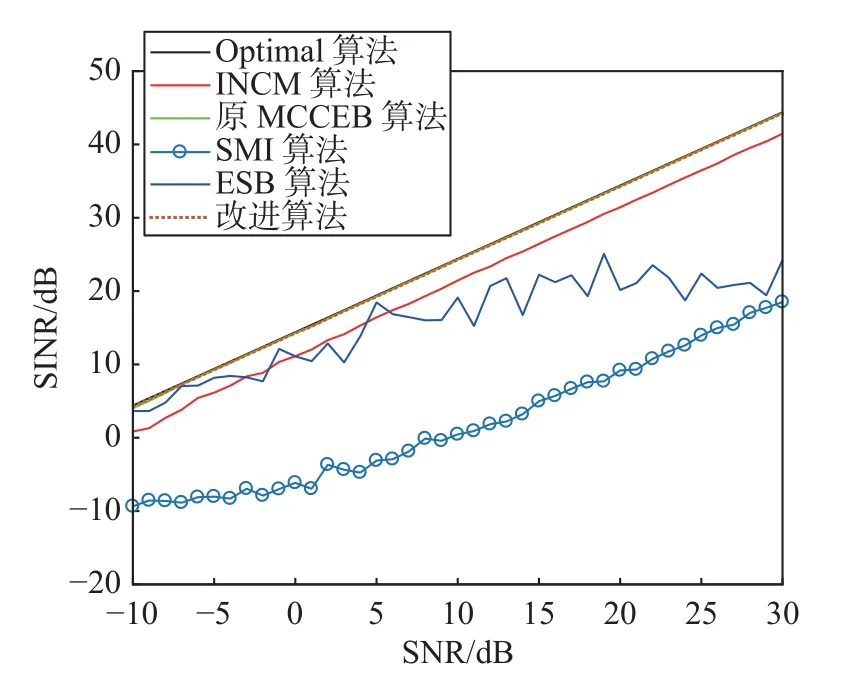
图5 几种算法在互耦情况下的输出SINR 曲线对比Fig.5 Output SINR curve comparison of various algorithms in the case of mutual coupling

3 结论

本文针对基于互耦系数估计的抗互耦算法在低输入SNR 的条件下波束形成器的输出SINR 曲线不理想的问题，对算法进行了改进，在输入SNR 低于输入SNR 门限时，用干扰信号的导向矢量参与互耦系数估计，当SNR 高于输入SNR 门限的时候，与原算法一样利用期望信号和干扰信号共同确定互耦系数.通过仿真对比分析，该算法提高了低SNR 下的抗互耦性能，与其他几种算法相比，抗互耦和抗干扰性能更好，具有一定的理论意义与工程价值.