电离层虚高对超视距雷达多站联合定位精度的影响

张旭辉 姜春华* 刘桐辛 杨国斌 赵正予，2

（1.武汉大学电子信息学院,武汉 430072；2.哈尔滨工业大学(深圳),深圳 518055）

引言

天波超视距雷达利用电离层对电磁波的反射实现对视距之外的目标探测，被广泛应用于军事领域，在国防体系中占有很重要的地位.天波雷达最早出现在二战期间，战后各国注意到高频信道传输的价值，纷纷投入研究，天波雷达技术得以不断的完善，我国天波雷达的发展也有40 多年的积累[1-2].

天波雷达的一个功能是进行超视距的目标定位，单基地的天波雷达可以获取远距离目标的位置，但是定位过程必须结合当时的电离层信息，往往需要额外的电离层探测设备进行同步的主动探测，比如电离层垂测仪、斜测仪、斜向返回探测仪等，这将会大大增加系统的复杂程度，使得雷达的成本大大增加，而且不利于电磁兼容的设计，对雷达性能会造成一定的影响，同时单站定位中的测向和测高误差会导致不能接受的误差[3-4].随着电子对抗技术的不断发展，单基地雷达在战场上的生存形势很不乐观，而收发分置的多基地雷达则有着很好的四抗性能，受到了各国广泛的关注[5].

在多基地天波雷达系统中，则需要考虑不同接收站点电离层的状态.电离层模式和实时状态会影响电波反射时的虚高，进一步对坐标配准产生系统性的误差，因此会给目标定位带来困难.在雷达系统中，测量过程存在电离层虚高、雷达回波到达角测不准的问题，严重影响目标定位的精度[6].

对于虚高的测不准，即使有较好的电离层诊断系统，虚高的测量误差也会在十几千米.贺承杰[7]的仿真试验表明，在进行大圆距离约为2 133 km的目标定位时，标准差为15 km 的电离层虚高测量误差引起的目标定位均方差为8.2 km.对于标准差为0.4°的方位角误差，在同等条件下会引入13.7 km的定位均方差，二者联合则会引入16.2 km 的均方差.贺青等[8]基于圆概率误差分析了在单站无源定位中电离层虚高误差对定位的影响.攸阳等[9]提出一种基于电离层射线追踪技术的时差定位技术，并在此基础上仿真分析了电离层参数对定位精度的影响，结果表明电离层测量误差对定位精度影响较大.

Cilliers 等[10]提出了一种计算机电离层断层扫描方法，此方法的效果比垂测仪好，可以提升电离层信息的估计精度，从而提高定位精度.为了提高测向性能，Svantesson 等[11]提出利用开关寄生天线的方向辐射模式进行测向的方法，使得测向的分辨率有了显著提升.当通过不同电离层传输的多个回波具有近似独立的衰落特性叠加在一起的时候，可能会导致更严重的跟踪问题，甚至使雷达完全失效.针对多径传输问题，可以采用交叉模糊性函数-方向搜索(cross ambiguity function-direction finding,CAF-DF)算法进行波达方向(direction of arrival,DOA)估计[12].

韩彦明[13]研究了虚高测量误差和方位测量误差对目标定位的影响，结果表明影响大圆距离解算误差的主要因素是虚高测量误差，基于此给出了可能的定位精度提升的途径(一个是电离图智能判读方法的改进，一个是利用信标回波自动检测和识别)，并且对无源信标定位修正方法进行了研究，通过实测目标数据比对，定位精度有所提高.宋君[1]对多站定位的误差进行了系统的研究，仿真结果显示三角站型比线性站型的精度更高，且在延展基线至300 km的情况后，仿真结果显示在一定范围里，接收站离主站距离越远，定位精度越高.此种方法虽定位精度很高，但需要准确知道电离层虚高信息.贺承杰[7]提出了一种短基线多站定位算法，并验证了这种方法的可行性.其原理是在单站定位的基础上，构建多个类似的方程，把方位角和电离层虚高当作未知量，直接解算出目标的位置，使得目标定位的精度大大提高.但是方程的联立求解需要假设各条电波路径的反射点虚高是一致的，否则会引入多余的变量，使得方程组没有唯一解.

本文利用短基线的两个电离层观测站点仙桃站和武汉站(相距约为90 km)，接收较远距离的四川道孚站和乐山站的电离层斜测信号，分析电离层反射虚高对短基线多站雷达目标定位精度的影响.

1 定位原理

多站定位的算法思想是基于单站定位原理构建多个方程，从而联立求解得到方程解.单站定位时，发射站发射的电波经目标散射后由接收机接收，记录时延t，可以求得群路径P=ct，c是真空中的光速.利用电离层探测设备可以得到电离层信息，比如通过斜向返回探测系统可以获得电子浓度剖面[14-15]，再通过射线追踪得到反射点虚高h，如图1(a)所示，其中T/R 表示收发同址的超视距雷达，O 表示目标，C 表示地心.结合地球半径R，运用Martyn 等效定理可以构建一个三条边长度已知的三角形，如图1(b)所示.

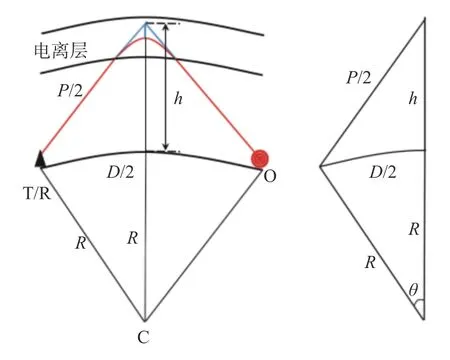
图1 单站有源定位示意图(a)和根据Martyn 等效定理构建的三角形(b)Fig.1 Schematic diagram of the single site location(a) and triangle constructed according to Martyn’s equivalence theorem (b)

在图1(b)中，可以利用余弦公式和弧长公式得到：

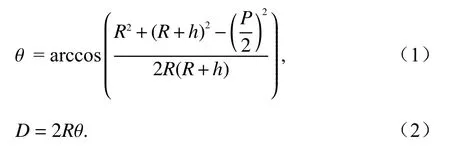
将式(1)代入到式(2)得到大圆距离D，也即单站定位的距离计算公式：

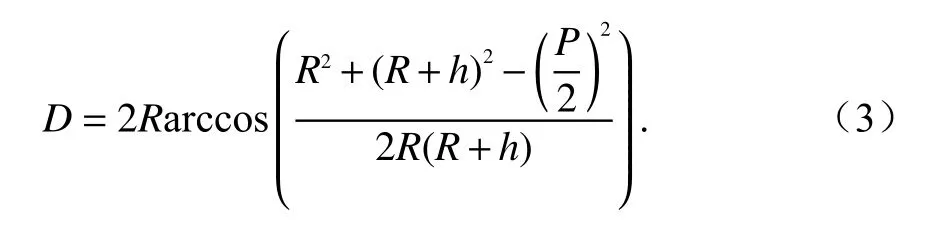
多站定位相当于构建了多个单站定位的方程，联立求解即可得到目标的经纬度，如式(4)所示：

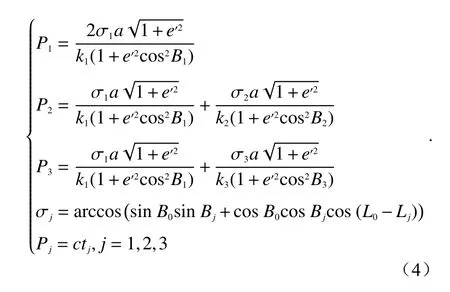
式中：Pj、tj(j=1,2,3,j=1表示主站)为由主站发出、j站接收的电波群路径和群时延；σj为j站到目标的大圆距离(单位为弧度)；a为地球大半轴，取6 378.245 km；为第二偏心率的平方，b为地球小半轴，取6 356.863 km；kj为由目标到j站对应的P-D 变换系数；(B0,L0)为 目标的经纬度；(Bj,Lj)为各个站点的经纬度；c是光速.

2 电离层虚高对目标大圆距离解算误差分析

多站定位算法假设多个反射点位置处的坐标配准系数一致即虚高一致，从而对方程组进行联立求解，而实际不同链路的反射点虚高并不一定相等，由此会引入多站联合定位的模型误差.

在大圆距离解算时，不同的链路采用一致的虚高会产生误差，如果该虚高比实际虚高大，会使得解算出来的大圆距离偏小，反之偏大，示意图见图2.

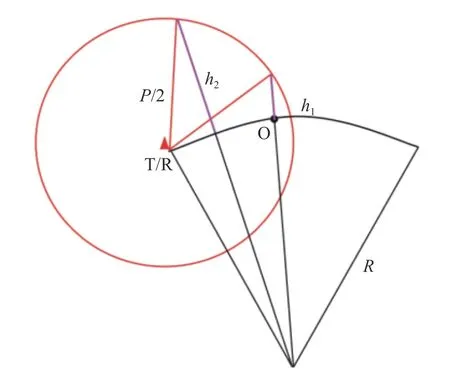
图2 虚高偏差对大圆距离解算的影响Fig.2 Effect of the virtual height deviation on the calculation of great circle distance

假设虚高一致，用h2代替实际的虚高h1去解算大圆距离，由于h2＞h1，得到的大圆距离会偏小.

进一步探究虚高对大圆距离的影响，对式(3)的两边进行求导得[13]：

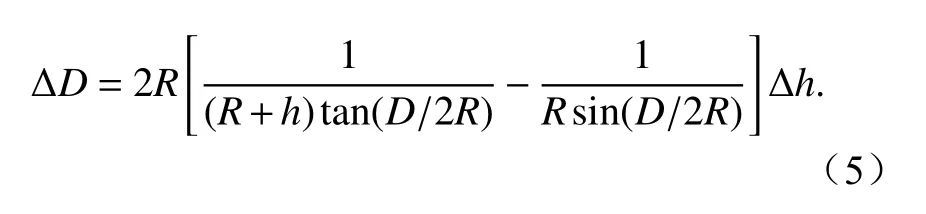
式中：ΔD是 地面距离误差；Δh是实际的虚高差.

3 试验与分析

由于超视距雷达进行目标探测时接收的回波信号是经由电离层反射的双程斜测信号，本次试验主要模拟的是目标经过电离层反射到达接收站点的单程斜测路径.在前期的电离层斜测试验中，周晨等[16]对电离层高频信道互异性进行了分析，发现双程斜测两条路径的群时延和散射函数都具有较好的互异性.因此本文近似认为双程斜测中目标返回信号和发射信号的路径是重合的，可以认为双程传输条件下的误差和单程条件下是近似一致的.

3.1 试验介绍

武汉大学电离层实验室开发研制的武汉电离层探测系统 (Wuhan Ionosphere Sounding System，WISS)具有电离层垂直探测、斜向探测和斜向返回探测等功能，为电波传播工程应用提供了一个良好的平台.本文利用四川乐山和道孚、湖北仙桃和武汉等地区部署的WISS 观测站进行本次验证试验.试验中四个站点的位置信息分别是：道孚(31.0°N，101.12°E)、乐山(29.6°N，103.75°E)、仙桃(30.2°N，113.53°E)、武汉(30.5°N，114.37°E)，站点分布如图3 所示.其中道孚-仙桃大圆距离1 190 km，道孚-武汉1 266.5 km，乐山-仙桃945 km，乐山-武汉1 026 km，仙桃-武汉87 km，工作方式为道孚、乐山同步发射，武汉、仙桃同步接收，由此可得道孚-仙桃、道孚-武汉、乐山-仙桃和乐山-武汉四条链路.由于试验时各探测系统收发异地，本系统采用时频同步模块(支持GPS 和北斗系统)为整个探测试验提供校准的时钟和秒脉冲，以保证各个站点之间的时频同步.另外，针对各站点探测系统的内部时延，试验之前在武汉站对其进行了统一校准.

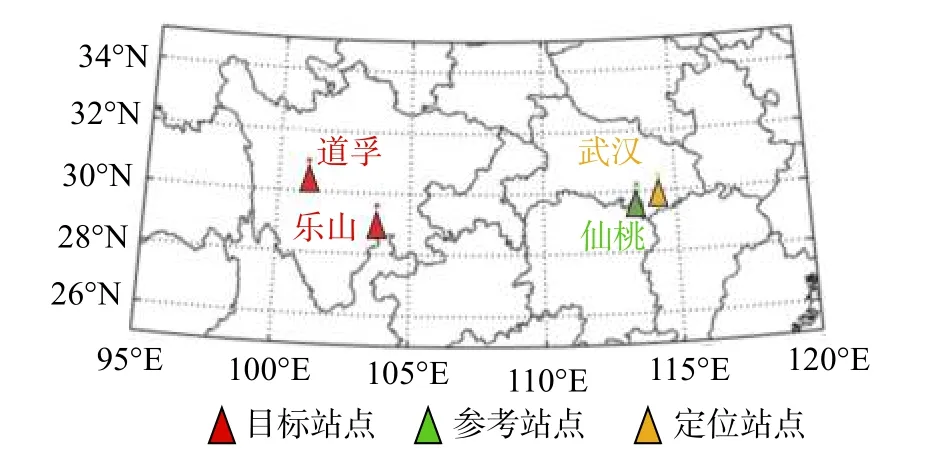
图3 四个试验站点的地理位置示意图Fig.3 Geographical location of Daofu,Leshan,Xiantao and Wuhan stations

在本次试验中，道孚和乐山模拟两个不同地面距离的目标，为目标站点，其发射的斜测信号模拟目标的散射信号；仙桃和武汉用来模拟多基地雷达定位中的两个接收站点，其中将仙桃站点作为参考站点，武汉站点作为解算和目标大圆距离的定位站点.

试验流程见图4，目标站点和参考站点的大圆距离Dref和群距离Pref已知，利 用Dref和Pref计算该条链路的电离层反射虚高，然后利用和定位站点测得的目标站点群路径信息P可以解算目标站点和定位站点的大圆距离D′，并和两者实际的大圆距离D进行比较分析，得出电离层虚高对大圆距离解算的影响.在整个目标站点的大圆距离的解算中，参考站点和定位站点使用同一工作频率.

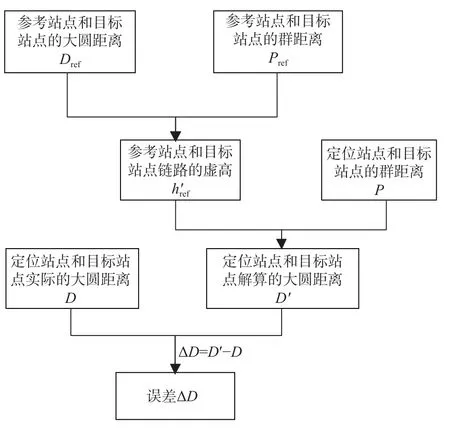
图4 大圆距离解算流程图Fig.4 Flowchart of the great circle distance calculation

3.2 数据处理

本次试验站点主要分布在我国的中低纬度，北纬30°左右，试验时间为2021 年的春季，三天平均的Dst 指数为-12.83，具体时间为3 月12 日至3 月14 日每天的7:30 至21:00.该时段处于太阳活动低年，且地磁活动较为平静.选取的数据时间间隔为15 min，去掉期间的异常数据，三天数据共计148 条，选取的数据主要集中在白天是因为这个时间段信号信噪比较大，人工判读群距离时引入的随机误差较小.

首先对于同一个目标站点比如道孚，在同一时刻选定一个合适的频点，尽可能使得武汉和仙桃站点接收的道孚信号的信噪比较大，再使用MATLAB软件人工判读当前频点对应的F2层回波群时延.软件界面示例见图5，回波图中左下方的是乐山站点的斜测信号，右上方的是道孚站点的斜测信号.

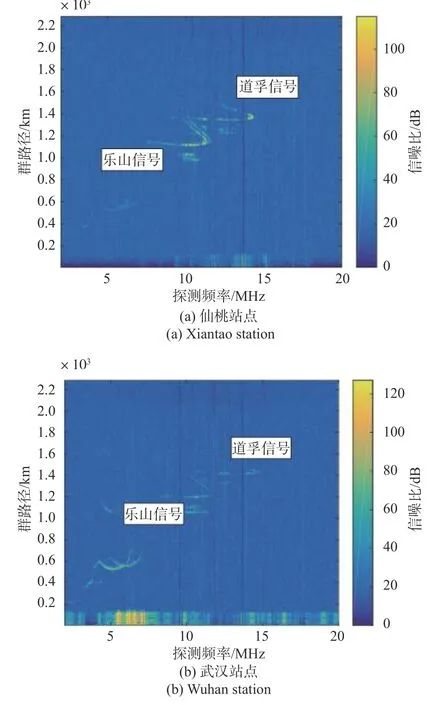
图5 仙桃站和武汉站接收的斜测电离图(2021 年3 月12 日15:00)Fig.5 The oblique ionograms recorded at Xiaotao and Wuhan stations at 15:00 on March 12,2021

3.3 结果分析

按上述试验方案和数据处理的方法，针对连续三天的试验观测数据，即可探究电离层虚高不一致对大圆距离解算的影响.利用道孚-仙桃的虚高解算道孚-武汉的大圆距离，结果如图6，相应时刻的频率见图7；利用乐山-仙桃解算乐山-武汉的结果见图8，频率见图9.

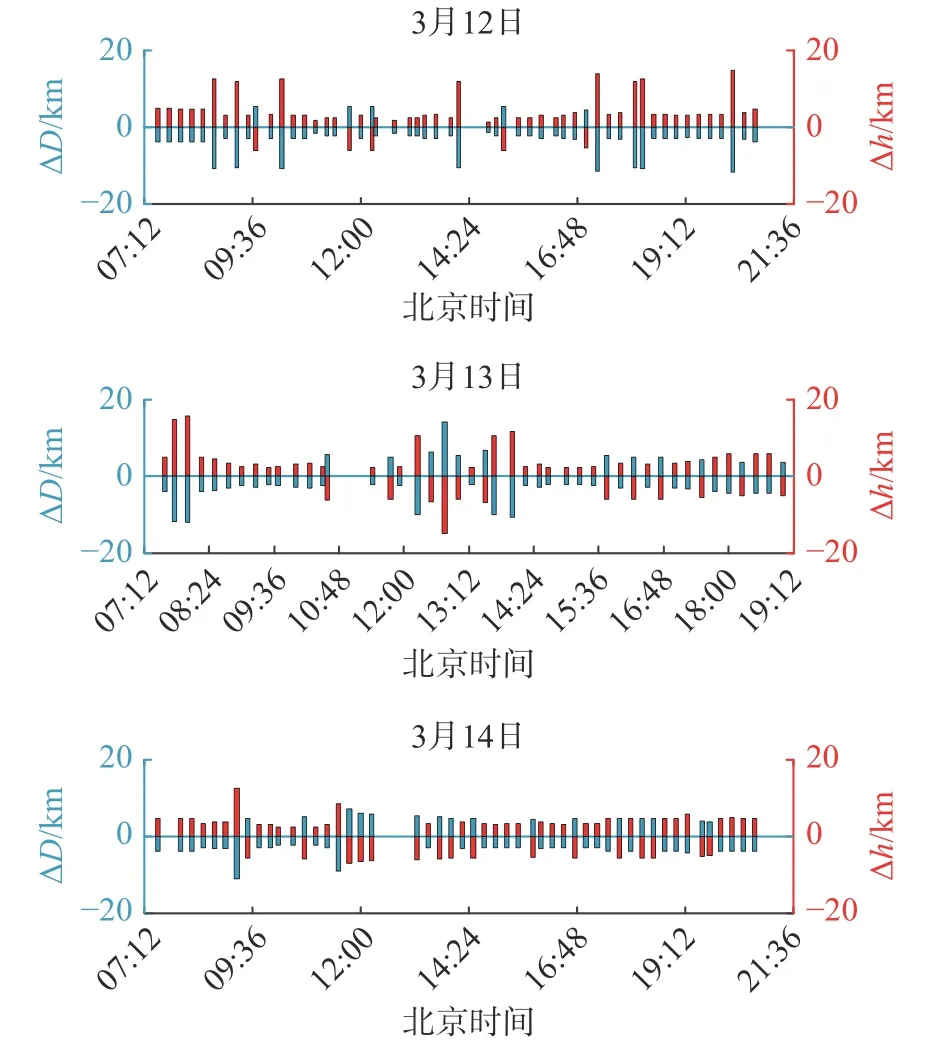
图6 道孚-武汉链路的真实虚高差和大圆距离解算误差Fig.6 Real virtual height deviation and calculated error of the great circle distance of Daofu-Wuhan link

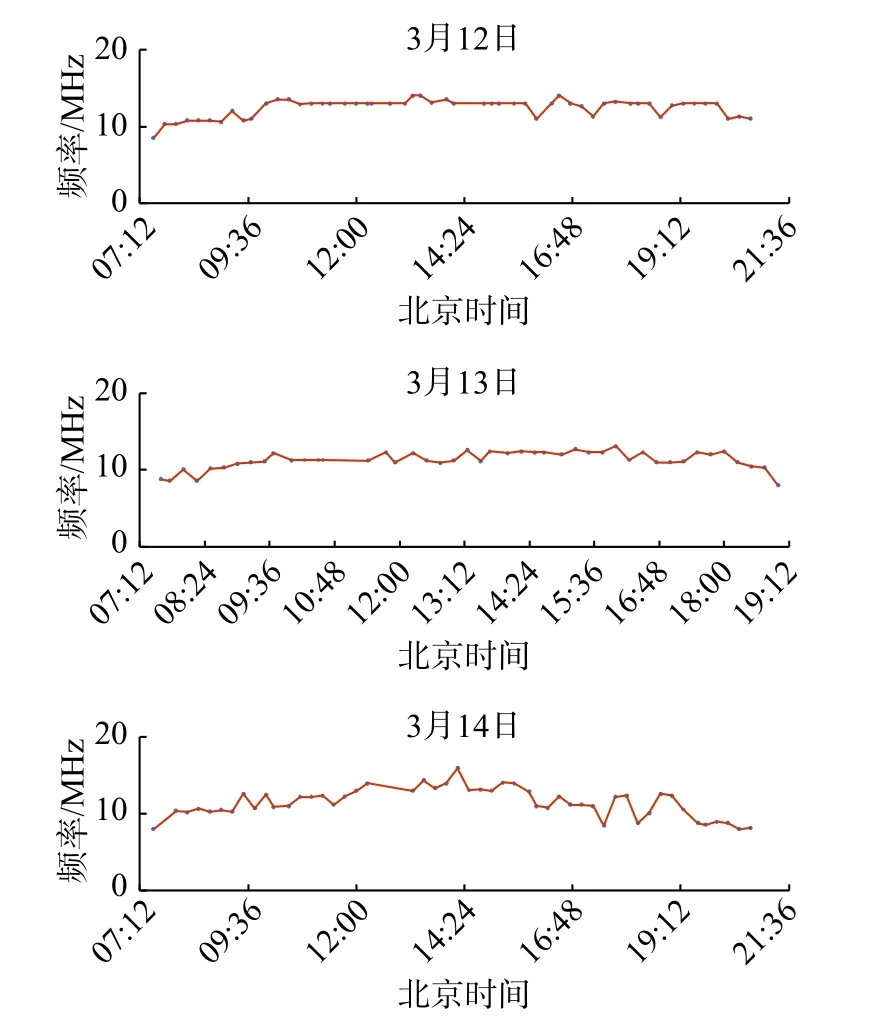
图7 道孚-武汉链路数据标定时选取的频率Fig.7 Frequency selected for data calibration of Daofu-Wuhan link

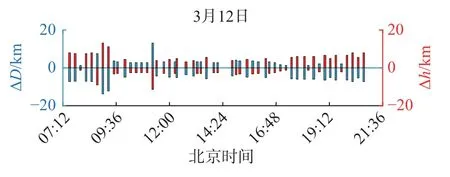
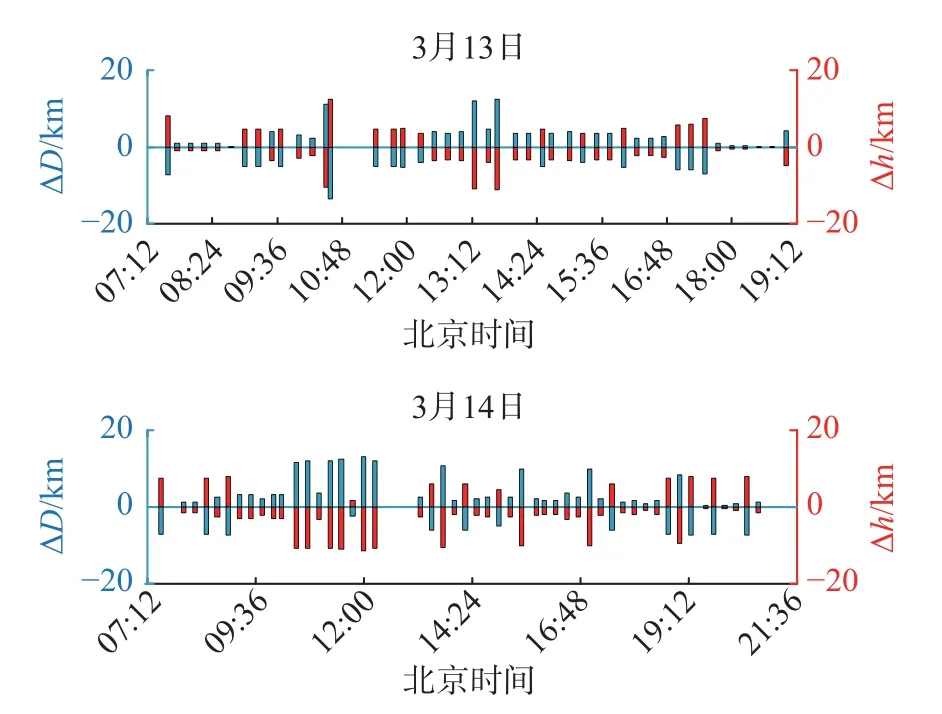
图8 乐山-武汉链路的真实虚高差和大圆距离解算误差Fig.8 Real virtual height deviation and calculated error of the great circle distance of Leshan-Wuhan link

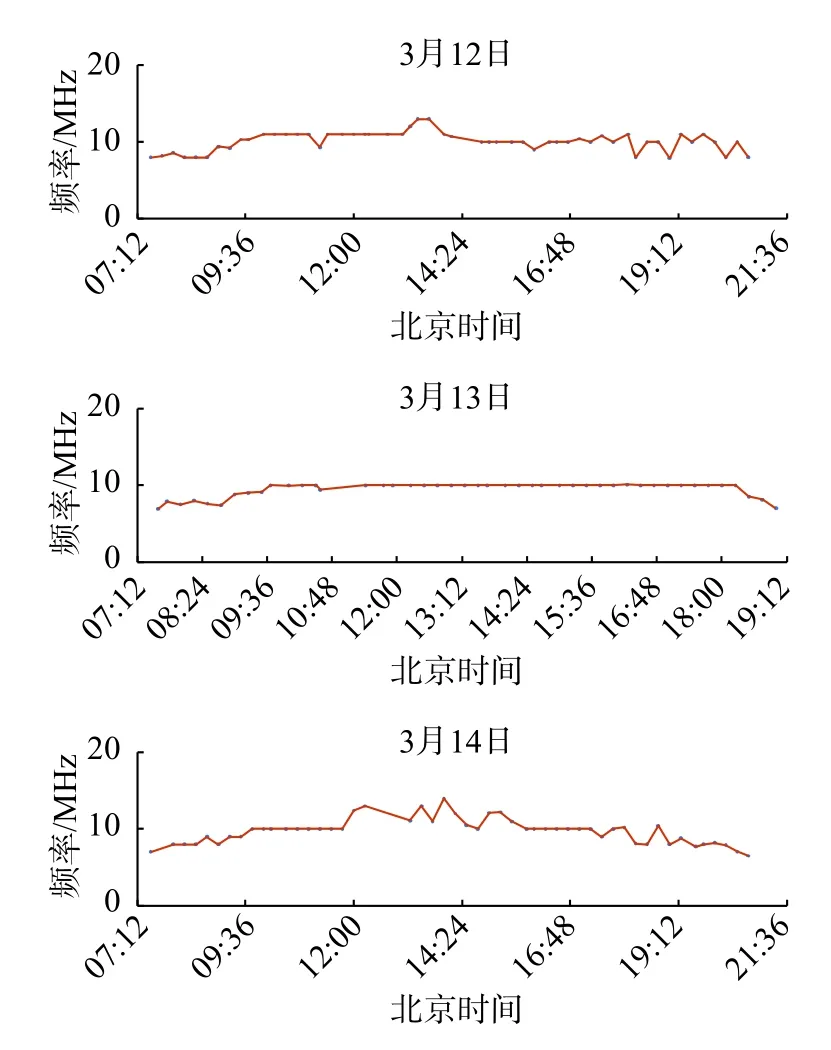
图9 乐山-武汉链路数据标定时选取的频率Fig.9 Frequency selected for data calibration of Leshan-Wuhan link

由图6、图8 可知，两条链路真实的虚高差和大圆距离的解算误差基本在-20～20 km.虚高差的大小和数据标定时选取的频率有关，不同的频率计算出的虚高差不同.虚高差和解算误差绝对值相差不大的原因是，根据式(5)计算出的 ΔD和 Δh的比例系数在1 左右.道孚-武汉链路早晨和黄昏时虚高差大都为正，说明晨昏时道孚-仙桃链路的虚高大于道孚-武汉链路，乐山信号的这一规律不明显.

三天数据的误差分析结果见表1 和表2，对于道孚、乐山两个站点来说，武汉链路的虚高均方根误差差别较小的原因是道孚-仙桃和道孚-武汉的链路中点相距43.3 km，乐山-仙桃和乐山-武汉的链路中点相距43.2 km，电离层区域不均匀性对二者的影响大致相同.

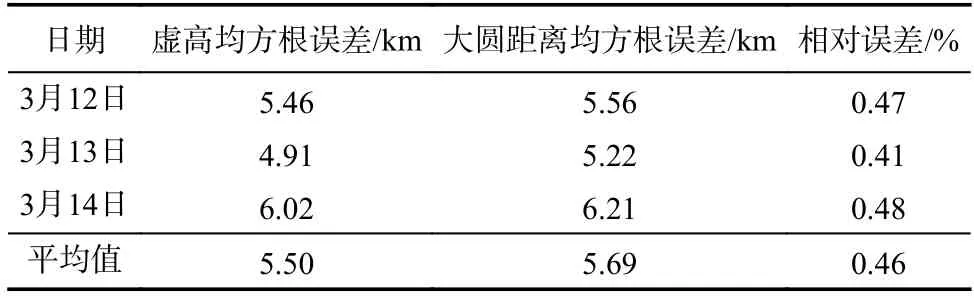
表2 乐山-仙桃的虚高解算乐山-武汉大圆距离的误差Tab.2 The error using the virtual height of Leshan-Xiantao link to calculate the great circle distance of Leshan-Wuhan link

由表1 可知，利用道孚-仙桃的虚高解算道孚-武汉的大圆距离，当发射站和接收站相距约1 260 km时，两条路径的虚高均方根误差约为5.82 km，相应的大圆距离的均方根误差约为5.02 km，相对误差约为0.34%.当目标站点和接收站点相距更近时(乐山-武汉，约1 000 km)，其对应的误差分别约为5.5 km,5.69 km 和0.46%.

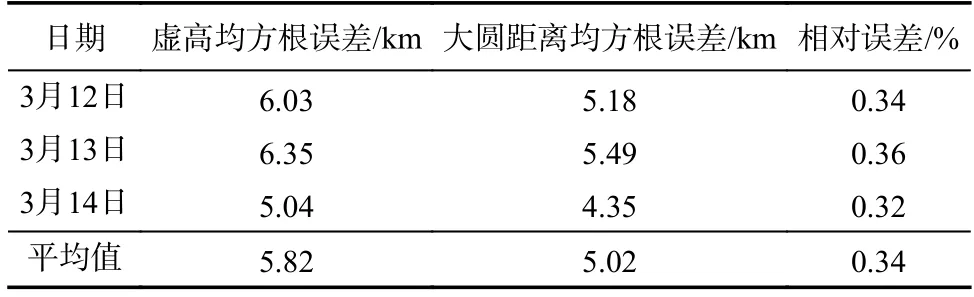
表1 道孚-仙桃的虚高解算道孚-武汉大圆距离的误差Tab.1 The error using the virtual height of Daofu-Xiantao link to calculate the great circle distance of Daofu-Wuhan link

道孚站点每天的虚高均方根误差都大于解算均方根误差，而乐山则相反，主要是因为乐山-武汉链路的大圆距离与道孚-武汉相比更小.根据前面推导的误差公式(5)可推出，对于道孚-武汉链路，虚高在299.6 km 以上时，大圆距离解算误差大于虚高差，而乐山-武汉链路的虚高只要在245.6 km 以上大圆距离解算误差就会大于虚高差，在实际探测中虚高在245.6 km 以上的偏多，就会导致上述情形.道孚-武汉链路的相对误差较乐山-武汉小，也和乐山-武汉大圆距离小有关.

在本次试验分析中，发现两条链路(道孚-武汉和乐山-武汉)的虚高和大圆距离误差没有相关性，这是因为在实际频点选择中，为了尽量减少误差，本文选取信噪比较高的频点，就是导致两个链路在群路径标定时，选取的频点不一致，由此导致两条链路的相关性不大.另外，关于道孚-武汉和乐山-武汉这两条链路相干性的分析，刘桐辛等[17]有详细的分析.

在本文的试验中，试验的链路主要在1 200 km 左右，当目标的大圆距离更远时，例如1 500 km 和2 000 km 时，假设实际虚高为200 km，虚高差为5 km，则根据公式(5)，对应的大圆距离解算误差和相对误差约为3.16 km、0.21%和2.71 km、0.14%，表明实际虚高和虚高差一定时，大圆距离越大，对应的解算误差和相对误差就越小.

4 结论

本文利用武汉大学自主研制的电离层探测系统WISS，以道孚、乐山为目标站点，仙桃为参考站点，武汉为定位站点模拟超视距雷达目标定位试验，基于相邻站点仙桃和武汉站的电离层探测数据，对短基线天波雷达的多站定位算法中电离层虚高对目标定位精度的影响进行了分析.结果显示在太阳地磁活动平静期间，当站点间的纬度接近且大圆距离在1 000 km 以上时假设虚高一致造成的大圆距离相对误差在0.5%以内，不过对于高精度定位应用而言，在该尺度下的站点布局定位时假设虚高一致则过于理想化.根据试验结果以及理论分析，可以从以下两个方面提高目标的定位精度以满足未来的高精度定位场景：

1) 降低不同站点的电离层虚高误差，使多站联合定位中的虚高一致性原则更加符合实际情况.为了实现这一点，在考虑雷达探测体制的情况下，需要尽可能地使接收站点更加靠近.

2) 降低雷达电波在电离层中反射的虚高，以此减小电离层虚高误差对目标定位误差的影响.本文的试验结果表明，在较低的电离层反射虚高中，即使电离层虚高误差较大，也能够得到较小的大圆距离误差.

在本文工作基础上，未来将考虑从以下方面进一步研究电离层状态对目标定位精度的影响：

1) 研究存在电离层多模多径效应情况下如Es 层和F 层同时存在，电离层虚高对目标定位精度的影响；

2) 探究在不同的布站尺度下假设虚高一致引入的误差分析.目前接收站之间的距离在90 km 左右，后期工作考虑更小尺度(如50 km，25 km 等尺度)布站情况下的试验分析，以探究超视距目标高精度定位的可能性.

3) 电离层纬度效应对目标定位精度的影响.由于目前发射站和两个接收站所在纬度的变化较小，两条电波反射点处的电离层情况差异不明显，使得最终的解算误差较小，将来会引入广东珠海站点和云南普洱站点，研究电离层虚高在纬度方向的变化对雷达定位的影响.