基于不同算法的高炉操作炉型聚类效果对比

鲁 杰，闫炳基，赵 伟，李 鹏，陈 栋，国宏伟

苏州大学沙钢钢铁学院，苏州 215137

高炉操作炉型是高炉投入生产后，经炉衬侵蚀、渣皮生成，由设计炉型逐渐演变而来的表征高炉状态的高炉内型.在高炉冶炼过程中，高炉操作人员大多通过冷却壁参数、操作参数，结合生产经验间接分析高炉操作炉型的变化情况，以此判断炉况的好坏[1-2].为保证高炉生产的优质、低耗、高产、长寿，就需要一个合理的高炉操作炉型.通过高炉冶炼过程参数，有效合理地表征高炉操作炉型的状况及其变化过程，并分析造成变化的原因，有利于高炉操作者及时调节高炉操作制度，优化生产过程.

大数据分析平台改善了传统工业的生产模式，对高炉炼铁生产具有重要指导意义.聚类分析是大数据中重要一环，借助大数据平台，国内外学者探索了高炉料面控制、煤气调度优化、中心煤气流分布情况监测、高炉操作炉型监控、铁水温度预测及铁水硅含量预测等技术[3-12]，有效优化了高炉冶炼过程，是冶金工业向智能制造转型的有力支撑.

K-Means、TwoStep 是现阶段常用的高炉操作炉型聚类算法[13-16]，但是对于不同聚类算法，应用效果的对照关系不甚明确.本文以高炉冶炼过程的冷却壁热电偶温度为表征参数，利用K-Means和 TwoStep 聚类算法进行聚类分析，结合算法原理及聚类结果研究不同聚类算法的效果差异，以期为高炉炼铁大数据分析中的聚类算法选择提供有利参考.

1 聚类算法

1.1 聚类算法的选择

聚类分析是数据挖掘技术中的一项重要技术，通过将数据集合划分成多个类，基于数据的特征将相似的样本归为一类，而相异的样本分置于不同的类中，以此确保类内样本的同质性及类间样本的异质性.随着数据挖掘技术应用方面愈发广泛，国内外学者将聚类分析引入高炉操作炉型的管理中，通过采用不同聚类算法对高炉冶炼数据进行分析，有效合理地表征高炉操作炉型的变化，对高炉生产有着重要的指导意义.

武森等[17]选择了K-Means 算法与层次聚类算法分别对高炉冶炼数据进行分析，实现了对高炉操作炉型波动与变化的实时监控，有利于操作人员及时准确地调整高炉操作.García 等[18]和Saxena等[19]在K-Means 算法的基础上引入了自组织特征映射（SOM），利用SOM 训练数据集，根据训练集的输出结果采用K-Means 进行聚类以获得更好的聚类结果，在可视化、解释模型方面取得了较好的效果.而在武钢5 号高炉操作炉型管理系统的开发过程中，陈令坤和李佳[16]针对K-means 算法对初始中心敏感、样本分布有要求的特点，对K-Means算法进行了一定的改进，聚类结果准确表征了高炉铜冷却壁的温度变化，并借助炉型变化与高炉利用系数的对应关系，初步获得了武钢5 号高炉的炉型变化规律.

曹英杰等[15]选用了TwoStep 聚类算法研究国丰1 号高炉操作炉型，对高炉冷却壁热电偶温度值进行聚类分析，确定了高炉透气性指数与炉型变化的规律，并通过实践证明聚类分析的结果能够有效监控炉型变化，指导高炉生产现场.而闫炳基等[14]考虑到评价炉型的指标多且重叠性大的问题，曾在TwoStep 算法的基础上引入主成分分析方法（Principal component analysis，PCA），从传统评价炉型的指标中生成3 个新的核指标以评价聚类结果，实践结果表明生成的核指标有效解决了指标多且重复性大的问题，优化了高炉操作炉型的管理.

上述研究进展中涉及的聚类算法特点如表1所示[20-25].K-Means 聚类算法是经典的基于划分的聚类算法，时间复杂度低，聚类效率高，聚类质量好，在高炉操作炉型聚类分析中应用较多，同时KMeans 算法也存在对初始中心敏感、对数据分布有要求的缺点，但陈令坤提出的改进方法是行之有效的，在对高炉操作炉型的管理中获得了优异效果[16].层次聚类算法的时间复杂度普遍较高，且ROCK、Chameleon 等典型算法并不支持大规模数据集[25]，层次聚类算法在高炉操作炉型的研究中应用较少，武森等也仅在研究中提到该方法的可行性.SOM 是一种基于模型的聚类算法，该算法存在时间复杂度高、不支持大规模数据集、聚类结果对模型参数敏感的缺点，其优势在于模型能够提供充分描述数据的方法，Saxena 等[19]虽然结合了K-Means 与SOM 充分发挥了其在可视化、解释模型方面的优点，但随着聚类算法的深入研究，判别分析、主成分分析等方法被用于聚类结果的解释中，Mckim 等[26]利用判别分析中的图形技术帮助使用者理解和解释集群，闫炳基等[14]则借助主成分分析解决了指标重复性大的问题，研究结果也表明判别分析与主成分分析方法在解释聚类结果时取得了良好的效果.TwoStep 算法是改进的BRICH 算法（层次聚类算法），降低了算法的时间复杂度，并能够自动确定最佳聚类簇数，具有较好的扩展性，在高炉操作炉型监控管理的应用中也表现出较好的效果.

表1 聚类算法分类及特点Table 1 Classification and characteristics of clustering algorithms

基于以上讨论，本文结合所研究数据对象的特征，选择了两种现阶段高炉操作炉型研究中常用的聚类算法— —K-Means 和TwoStep 算法，对高炉炉身冷却壁热电偶数据进行聚类分析，并借助合适的聚类有效性评价指标，研究不同算法的聚类效果差异，以期为高炉炼铁大数据分析中的聚类算法选择提供有力参考.

1.2 K-Means 算法、TwoStep 算法原理

（1）K-Means 聚类的算法思想[27-28]是按照样本之间距离，将n个样本点划分为k个类，使得相似的样本尽量被分到同一个类，其衡量相似度的计算方法为欧氏距离.

K-Means 算法的具体步骤为：

①对全部n个对象，随机选择k个对象作为一个类的中心，代表将生成的k个类；

②计算其他对象到聚类中心的距离，分派对象至距离最近的簇内；

③针对每个类计算其所有对象的平均值，作为所有对象的新中心值；

④根据距离最近原则，重新分配数据；

⑤返回③直至无变化，结束聚类.

（2）TwoStep 两步聚类算法是BIRCH 层次聚类算法的改良方法，加入了自动确定最佳簇数量的机制，使得TwoStep 算法更加实用[26].

该聚类算法可分为预聚类阶段和聚类阶段.在预聚类阶段，采用了BIRCH 算法中聚类特征树生长的思想，先遍历一遍数据，生成聚类特征树的同时，预先聚类较为密集的数据点，形成诸多子簇.在聚类阶段，以预聚类阶段的子簇为对象，利用凝聚法逐个合并子簇，通过AIC 准则（Akaike information criterion）、BIC 准则（Bayesian information criterion）以及类别间最短距离确定最优类别数作为聚类终止的条件.

1.3 聚类有效性评价指标

聚类有效性评价指标分为内部指标和外部指标两类，两者的区别在于是否将外部信息用于聚类评价[29].在不考虑外部信息时，内部指标是利用数据集的空间几何结构信息评估聚类结构的优劣.在许多场景中常有缺少外部标签可用的情况，内部指标是聚类评价的唯一选择.聚类有效性评价的内部指标主要包括Compactness、Separation、Davies-Bouldin indicator、Dunn indicator 和Silhouette coefficient，这些评价指标的计算公式或方法如表2所示[25,30-32].

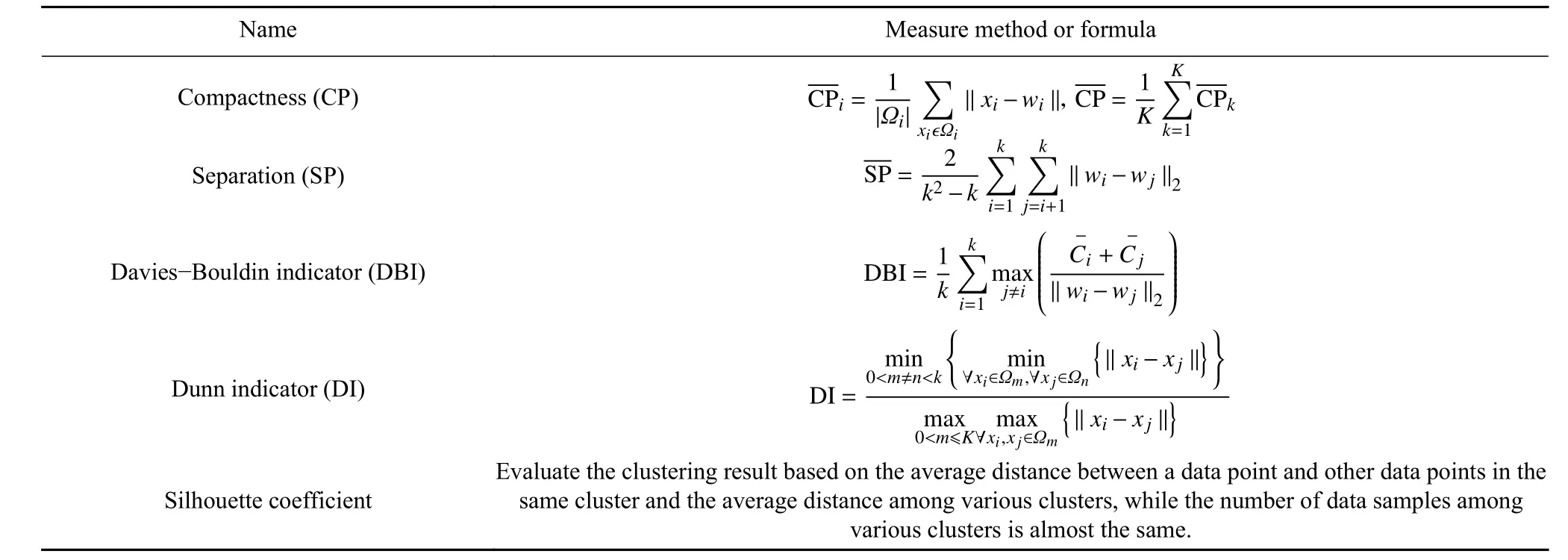
表2 聚类评价指标Table 2 Cluster evaluation index

Compactness 计算了每一类的类内各点到聚类中心的平均距离，但并没有考虑类间距离；Separation 计算了各聚类中心之间的平均距离，但没有考虑类内效果；Davies-Bouldin indicator 和Dunn indicator 考虑了类内效果与类间效果两方面，对聚类效果的评价更为全面；Silhouette coefficient 适用于数据结构清楚、各簇样本数目相差不大的情况[33]，而本文所选两种算法的聚类结果中各簇样本数目有明显差异，故而Silhouette coefficient 并不适用.基于五种聚类评价指标的特点，本文选用Davies-Bouldin indicator（DBI）和Dunn indicator（DI）作为评价依据.

2 基于不同聚类算法的高炉操作炉型聚类

2.1 数据处理

K-Means 和TwoStep 聚类算法在聚类过程中常会受到数据集中样本或是相似性度量函数的影响，难以达到最佳的聚类效果.因此，在聚类分析前对数据集进行处理能够使聚类结果更为理想，本文在借鉴张鸿雁等[27]与刘叶等[28]研究思路的基础上，在聚类前对数据集作如下处理：

（1）对于聚凸数据集以及中心点的问题，在数据集中确定一个端点，对所有个案到端点的欧氏距离排序，从而可以根据新的有序样本确定各个初始中心；

（2）对于异常点敏感的问题，聚类分析前已经去掉了缺失数据以及异常点数据；

（3）对于相似性度量函数，由于在第（1）步中采用欧式距离对数据集重新排序，因此确定采用欧式距离作为相似性度量函数，可以减少相似性度量函数对聚类结果的影响.

本文采用的数据是国内某钢铁厂高炉炉身热电偶的31986 条历史冶炼数据（考虑数据缺失、中途休风等影响已去掉无效数据），通过高炉炉身不同高度的冷却壁及耐火材料处安装的测量电偶，可以获得高炉炉身沿纵向8 层热电偶（第6、7、8、9、10、11、12、14 段冷却壁，第13 段无热电偶）测得的温度变化，以冷却壁温度为原始数据集对高炉操作炉型进行聚类分析.高炉各段冷却壁位置如图1 所示.

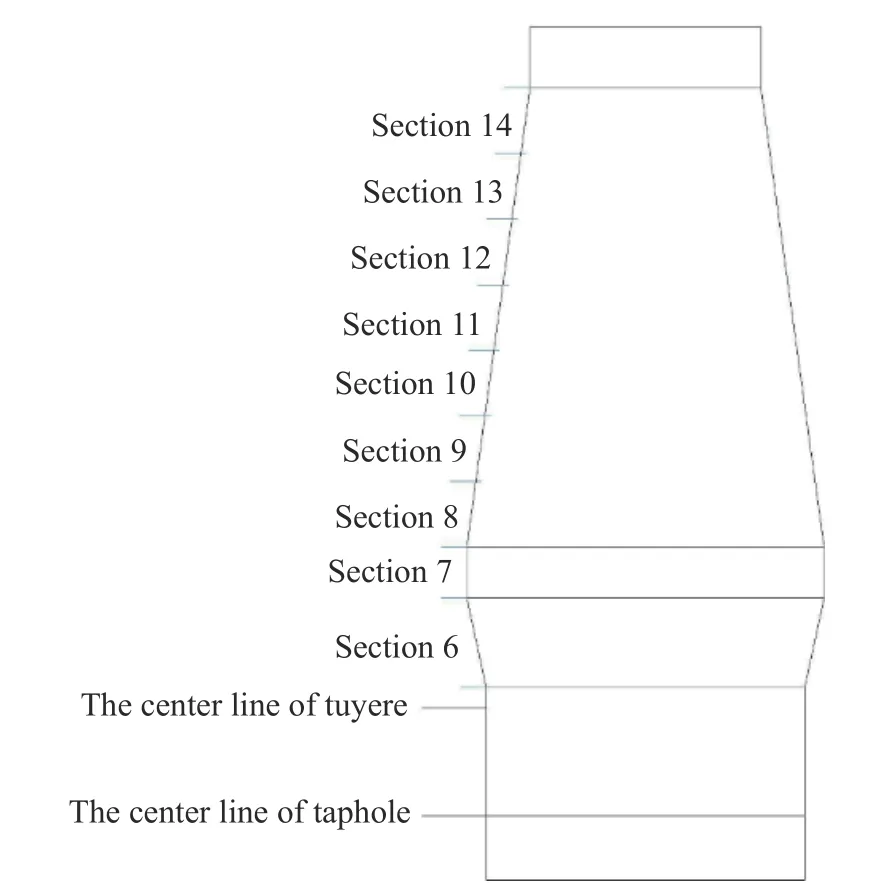
图1 高炉各段冷却壁位置示意图Fig.1 Position of a cooling stave in each section of a blast furnace

2.2 聚类簇数的确定

本文利用DBI 和DI 指标评价聚类效果，选择聚类结果最佳时的聚类簇数为最优方案.

在用聚类算法对高炉操作炉型聚类分析时，考虑到炉型分类的具体情况，即聚类簇数过少时评价炉型的精度不够，聚类簇数过多时会有部分类数据过少不具备代表性，因此将聚类簇数的范围限制在5 至12 类，DBI 和DI 评价指标的结果如图2 所示.

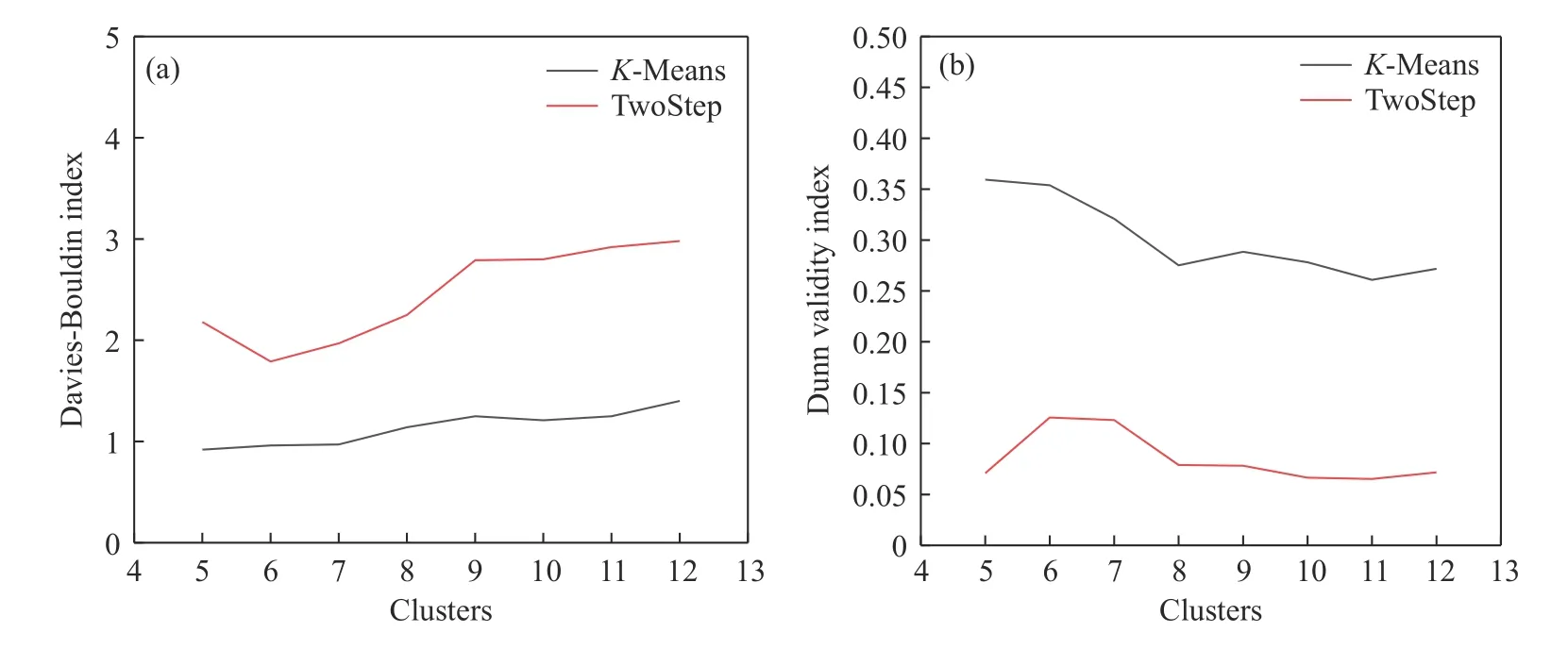
图2 不同聚类簇数的DBI 和DI 指标结果.(a) DBI 评价指标；(b) DI 评价指标Fig.2 Result calculation of a cluster evaluation index for various numbers of clusters: (a) Davies-Bouldin index；(b) Dunn validity index

根据表2 中DBI 和DI 指标的计算方法可以看出，DBI 评价指标结果越小，DI 评价指标越大，意味着更小的簇间相似性以及更大的簇内相似性，代表了聚类效果较优的情况.从图2（a）可以看出，TwoStep 算法的DBI 评价指标在聚类簇数为6 时最低，聚类结果在此处最优，而K-Means 算法的聚类结果整体优于TwoStep 算法的聚类结果，当聚类簇数在5 至7 时，聚类效果相差不大，聚类簇数＞7 时，DBI 评价指标呈现上升的趋势.于图2（b）中，DI 指标的评价结果也呈现K-Means 算法聚类结果整体优于TwoStep 算法聚类结果的趋势，Two-Step 算法的DI 评价指标在聚类簇数为6 时最大，聚类结果此处最优，K-Means 算法的DI 评价指标在聚类簇数在5 和6 时较大，明显优于聚类簇数＞6 时的聚类结果.

综合TwoStep 和K-Menas 算 法的DBI 和DI 评价指标结果，可以得到结论，在本文所选的样本数据及数据特征基础上，聚类簇数为6 时，两种算法的聚类结果普遍更优.

2.3 聚类结果

关于高炉操作炉型的监控研究，由于对象高炉的不同，聚类簇数的差异是一定的.本文根据DBI 和DI 指标运算结果，确定目标高炉操作炉型的最佳聚类簇数为6 类.K-Means 与TwoStep 算法的聚类簇数为6 类时，6 类炉型冷却壁各段温度分布如图3 和图4 所示.

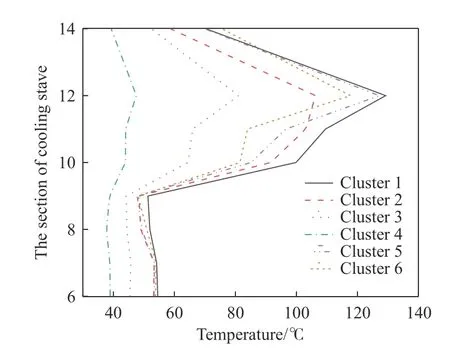
图3 K-Means 聚类结果中6 类炉型冷却壁各段温度分布Fig.3 Temperature distribution of each cooling stave of six furnace profiles by K-Means clustering algorithm

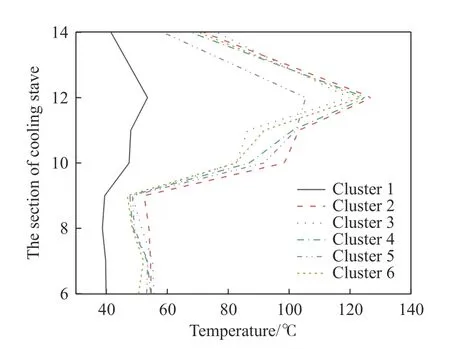
图4 TwoStep 聚类结果中6 类炉型冷却壁各段温度分布Fig.4 Temperature distribution of each cooling stave of six furnace profiles by TwoStep clustering algorithm

从图3 和图4 可以看到，利用K-Means 与Two-Step 算法分别对高炉冷却壁测温热电偶数据进行聚类分析，聚类结果中各类间区分明显，均有效表征了高炉不同时期的操作炉型状态.K-Means 与TwoStep 的聚类结果中高炉冷却壁温度有如下特点：冷却壁温度于第11～12 段相对较高，第12 段冷却壁温度最高（K-Means 聚类结果中第12 段温度最大值为130.7 ℃，TwoStep 聚类结果中第12 段温度最大值为127.1 ℃）；两种聚类结果中均存在一类高炉特殊时期的炉型（K-Means 聚类结果中Cluster 4 与TwoStep 聚类结果中Cluster 1）；K-Means聚类结果中Cluster 3 与TwoStep 聚类结果中各类的相差最为明显.对于这些特点，只依赖聚类结果难以分析，因此进一步分别从聚类簇内数据分布、聚类算法原理以及炉型物理含义的角度，分析KMeans 与TwoStep 的聚类结果有何不同，并判断当聚类簇数为6 时，K-Means 与TwoStep 的聚类效果哪种更好，更适用于高炉操作炉型的管理.

3 聚类结果分析

3.1 聚类簇内数据分布

TwoStep 聚类效果在簇数为6 与7 时表现出很大差别，通过汇总簇内数据的分布情况，分析簇数由7 减少至6 时减少的一簇中数据流向.簇数为6、7 时数据分布如图5 所示.

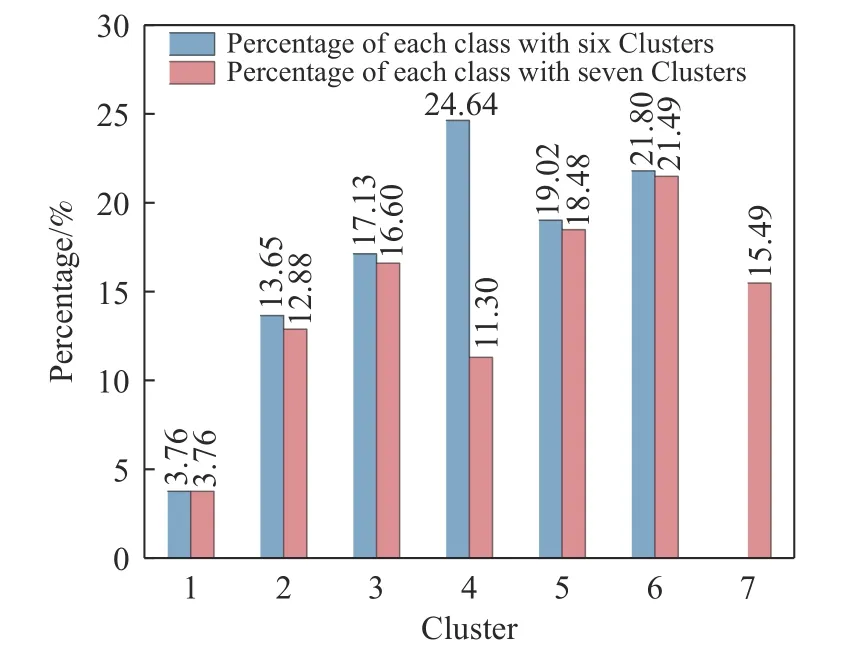
图5 TwoStep 聚类结果中簇数为6、7 时数据分布Fig.5 Data distribution when the numbers of clusters are six and seven by TwoStep clustering algorithm

从图5 可以看到，簇数为6 时的第4 类数据量占比为24.64%，与簇数为7 时的第4 类和第7 类的数据量占比之和（26.79%）基本接近，前者和后者的两类之间的数据对应匹配情况超过90%，而其他各类从数据量占比上也具有较好的对应性.根据DBI 和DI 评价指标的计算公式，可以认为簇数为7 时聚类效果更差的原因在于其第4 类与第7 类的簇间距离较小.当缩减聚类簇数时，相似的两类被合并为了一类，使得簇数为6 时的聚类结果明显优于簇数为7 时的结果.

K-Means 算法在聚类簇数为6 时的数据分布如图6 所示.

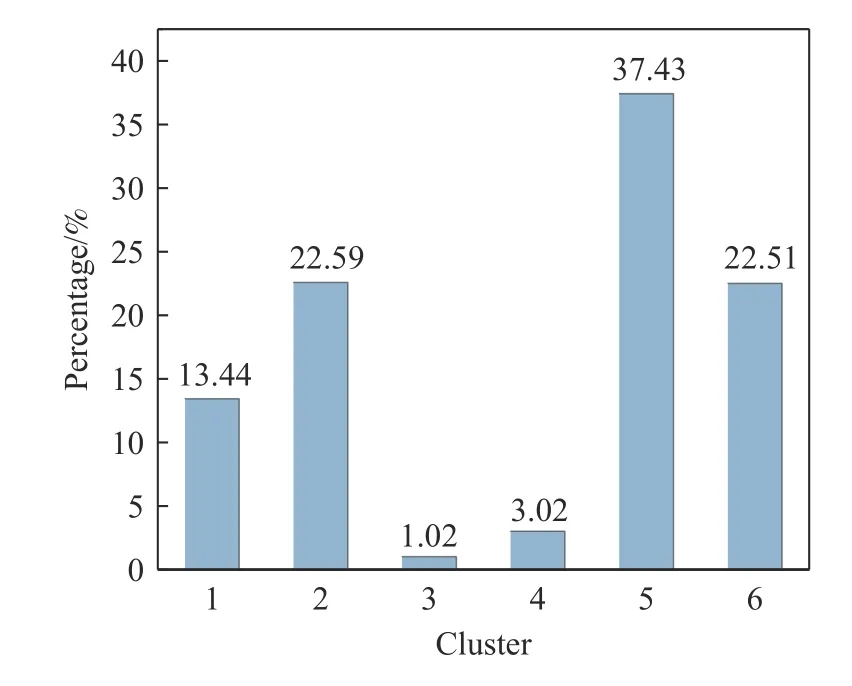
图6 K-Means 聚类结果中簇数为6 时数据分布Fig.6 Data distribution when the number of clusters is six by K-Means clustering algorithm

比较图5 与图6 可以发现，当聚类簇数均为6 时，K-Means 与TwoStep 聚类算法的数据分布差别很大.K-Means 聚类结果的数据分布更为集中，占比最多的一类达到了37.426%，而TwoStep 聚类结果占比最多的一类占比只有24.636%.同时，KMeans 聚类结果中存在两类占比极少，数据的分布情况体现了K-Means 聚类结果的簇内数据更为集中，簇间差别较大，验证了DBI 和DI 评价指标对聚类簇数为6 时的评价结果，可以得到结论：在本文所选的样本数据及数据特征基础上，K-Means 算法的聚类结果优于TwoStep 算法的聚类结果.

3.2 聚类算法原理比较

从聚类结果的数据分布以及DBI、DI 评价指标的比较，可以得到K-Means 聚类结果更优的结论.本节从聚类算法原理角度，讨论K-Means 算法与TwoStep 算法之间的优劣[34].

K-Means 算法根据事先确定的类别数选取不同对象作为聚类中心点，以欧式距离为相似度标准分派数据，再重新确定聚类中心，直至聚类结果收敛，这样的聚类过程与TwoStep 算法构造CF 树后采用凝聚法合并数据簇相比，有效地简化了算法，减少了K-Means 算法的时间复杂度.同时，Two-Step 算法采用凝聚法合并数据簇也决定了其在大数据样本处理能力上逊色于K-Means 算法，且由于算法在构造CF 树后采用凝聚法合并相似簇，这种合并子簇方法的不可逆性导致聚类算法无法重新合并或分离簇优化聚类结果.

在衡量相似度的标准上，K-Means 采用了欧氏距离，而TwoStep 使用了对数似然距离，这是统计理论中衡量簇与簇相异度的方法.不同的相似度衡量标准对聚类结果的影响很大，需要选用合理的衡量指标进行聚类分析.

能够自动确定类别数是TwoStep 算法的最大特点，TwoStep 算法可以通过AIC、BIC 以及类别间最短距离自动确定类别数.而K-Means 算法需要事先给定聚类数K值，K值的确定也会影响算法的最终聚类结果.

对于数据中的异常点，TwoStep 可以自动将其归类至最近簇中，但K-Means 对异常点没有有效的解决方法，异常点的存在会对聚类结果产生严重影响.本文在聚类分析前剔除了数据集中的异常点，因此K-Means 算法才得到了较好的聚类结果.

从聚类算法原理来看，K-Means 和TwoStep 算法均有其优点，但算法本身也存在其不足之处.两种算法本身并没有优劣之分，只是针对不同特性的数据集和特定应用场景，两种聚类算法对数据集的处理能力与处理结果存在差异.

3.3 炉型分类的物理含义

簇数为6 时，K-Means 与TwoStep 算法的聚类结果如图7 所示.

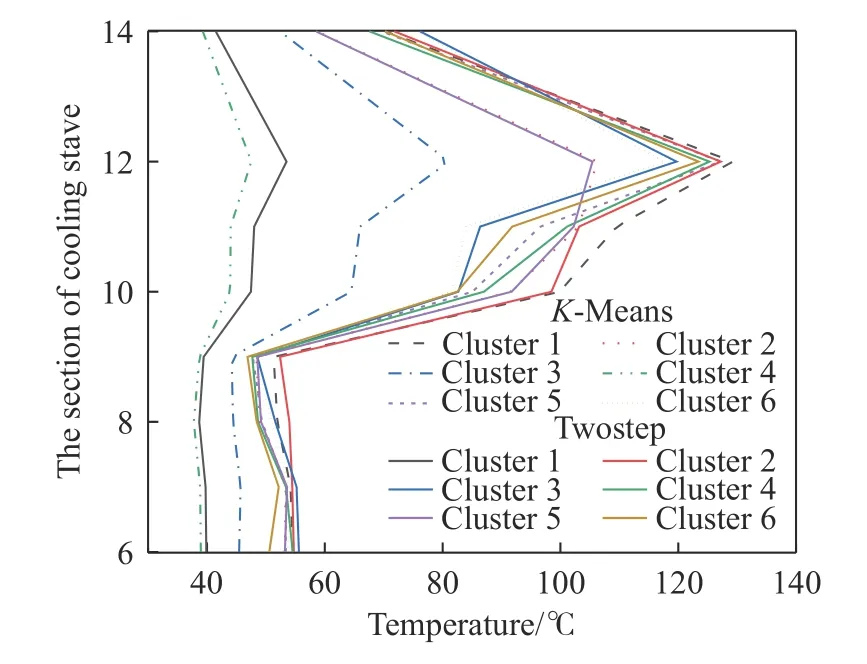
图7 K-Means、TwoStep 聚类结果（簇数为6）Fig.7 K-Means,TwoStep clustering results (number of clusters is 6)

从图7 可以看出，高炉炉型第6～9 段冷却壁温度相对10～14 段（除13 段无热电偶）温度较低.温度差异明显主要在于其冷却制度的不同，6～9 段为轧制铜与铸铜冷却壁，冷却效果较好，10、11 段为铸钢冷却壁，12、14 段为铸铁冷却壁，铸钢、铸铁冷却壁的冷却效果不如铸铜冷却壁[35-36].

对比每段各自冷却壁温度，当温度变化，基于炉型聚类结果可以判定操作炉型的变化状态，当操作炉型发生变化时，可能是由以下原因造成的：

（1）该段渣皮脱落较多，脱落频率较高，因此炉壁内衬相对较薄，热电偶温度上升；

（2）此段边缘气流有发展趋势，温度上升，此时可以根据现场需要对上部布料角度进行调整或加大边缘负荷等操作抑制边缘气流发展；

（3）如果出现温度长时间持续上升，则需要现场及时采取相应措施，对高炉下部风口进行调整，避免炉温继续升高.

因此，现场人员可以通过对高炉操作炉型的观察和监控，根据炉型整体变化情况采取相应的调控措施.

4 结论

本文以国内某钢铁厂高炉炉身热电偶温度值的31986 条历史冶炼记录为数据集，分别选择KMeans、TwoStep 算法对高炉操作炉型进行聚类.结合算法原理以及DBI、DI 评价指标对两种聚类算法进行比较，结果显示：

（1）通过DBI 和DI 评价指标比较两种算法在聚类簇数不同时的聚类效果，确定了最佳聚类簇数为6，此时K-Means 和TwoStep 算法都能得到更好的聚类结果.

（2）从聚类原理来看，K-Means 与TwoStep 算法并没有优劣之分.从聚类结果上来看，在本文所选的样本数据及数据特征基础上，K-Means 算法的聚类结果明显优于TwoStep 算法的聚类结果.

（3）分析炉身冷却壁热电偶温度变化尤其是操作炉型发生变化时的原因，主要包括：渣皮脱落导致的炉壁内衬变薄，边缘气流呈发展趋势，高炉下部风口影响等；高炉操作炉型聚类结果是对影响炉型状态的各个原因的综合显现，对其类别变化的跟踪，可为上下部调剂提供关键的指导信息，对于生产过程的及时调控具有重要的意义.