基于WOA-BP神经网络的锂离子电池健康状态估算

薛太林，张 超，闫来清，吴 杰，靳玉祥

（1.山西大学电力与建筑学院，山西 太原 237016；2.国网山西省电力公司阳泉供电公司，山西 阳泉 045000；3.山西国锦煤电有限公司，山西 交城 030500）

0 引言

锂离子电池具有能量密度高、自放电率低、循环寿命长、环境友好等优点，在电动汽车及储能系统等领域有着广泛的应用［1］。电池管理系统（Battery Management System，BMS）旨在对电池提供监测、诊断和控制功能，以提高其稳定运行能力，其中锂离子电池的健康状态（State of Heath，SOH）是BMS的关键指标之一，可反映电池的老化程度，实现锂离子电池SOH 的准确估计，及时剔除老化电池，对储能系统至关重要，从长远看，对老化电池回收并梯次利用，最大效率使用电池剩余价值，促进行业绿色健康发展也具有重要意义［2］。

目前，锂离子电池SOH的估计方法一般为两类：1）基于模型的方法。该方法又分为基于机理建模和基于经验建模。基于机理建模通过研究电池内部物理和化学反应，分析电极材料热电特性变化规律，从电池的设计制造角度进行研究。文献［3］指出固体电解质界面膜（Solid Electrolyte Interphase，SEI）与电池容量衰减的关系，但该类方法无法实现在线估计，仅适合生产从业人员。基于经验建模通过基本电路电子元件建立等效模型来模拟电池内部反应的静动态性能，并将SOH 估算问题转化为模型参数辨识问题［4］，例如程泽等人，利用改进的无迹卡尔曼滤波算法对电池的容量和内阻两个特征参数，同时更新实现SOH 的估算［5］。但这类方法对模型参数精度依赖性较高，存在参数辨识困难、普适性差等问题。2）基于数据驱动的方法。该类方法将电池看成“黑箱”系统，无须了解电池内部复杂的化学反应，通过机器学习算法并利用数据对输入与输出进行非线性拟合。文献［6］利用增强学习并结合改进的自适应提升算法，有效防止了过拟合问题，实现SOH 的在线估计。但也存在影响因素众多时训练较为耗时、对噪声敏感，且不能保证是最优解等问题。BP 神经网络具有强大的非线性映射能力以及柔性的网络结构［7］，文献［8］基于传统BP 神经网络进行锂离子电池健康状态估算，但参数容易陷入局部最小值，收敛时间较长。文献［9］采用了萤火虫算法优化的BP 神经网络，解决了参数陷入局部最优问题，但引入了等效电路模型参数辨识误差，SOH 估算精度较低，模型泛化能力差。

为有效解决上述问题，本文综合锂离子电池健康状态多种影响因素，基于BP 神经网络结合鲸鱼群优化算法（Whale Optimization Algorithm，WOA）对网络参数进行优化，提高了网络的全局搜索能力，并针对传统鲸鱼群算法应对复杂情况局部寻优能力不强的问题，引入了非线性收敛因子，在保证网络具有良好的全局搜索能力下提高了收敛速度。

1 SOH定义与预测网络构建

由于锂离子电池健康状态受多种因素影响，且SOH 是状态量，无法直接测量，须借助其他可观测量即健康因子（Health Indicator，HI）来间接表征［10］，目前SOH 的定义并没有统一的表达式，一般来说可以从锂离子电池最大可用容量或欧姆内阻值等角度去定义。本文采用欧姆内阻值来表征SOH，由马里兰大学公开的锂离子电池老化数据如图1所示。由图1可知，随着锂离子电池循环充放电次数的增加，欧姆内阻会逐渐增大，增大趋势具有非线性和一定的波动性，对SOH的定义［11-13］为

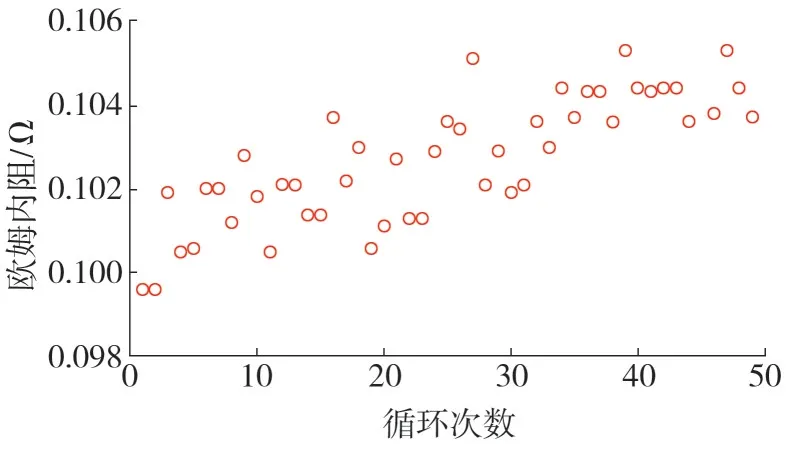
图1 锂离子电池欧姆内阻变化情况

式中：RN为锂离子电池初始欧姆内阻；R0为电池当前循环状态下的欧姆内阻。

神经网络是一种“连接主义”机器学习技术［14］。本文采用多层前馈神经网络，根据万能近似定理［15］（Universal Approximation Theorem，UAT），选择3层神经网络，且每层神经元个数不作限制。共包括输入层，隐含层和输出层，每层由多个神经元组成，同层及跨层神经元之间没有连接。网络结构如图2所示。

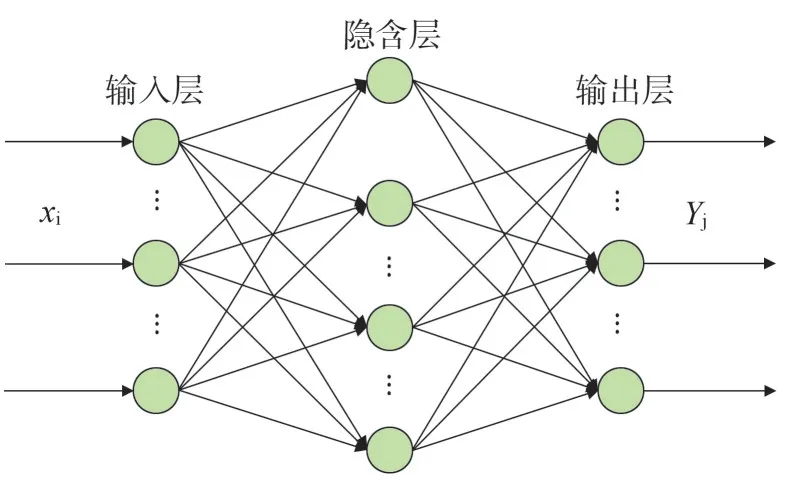
图2 三层神经网络结构

1.1 网络训练算法

神经网络的学习过程就是确定各个功能神经元之间的权值（Connection Weight，CW）以及自身偏置。误差逆传播（Error Back Propagation，EBP）算法，可以有效解决神经网络训练问题，前向传播过程为：

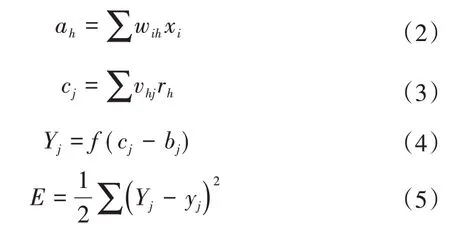
式中：ah为隐含层第h个神经元的输入；cj为输出层第j个神经元的输入；wih为输入层第i个神经元与隐含层第h个神经元之间的连接权值；vhj为隐含层第h个神经元与输出层第j个神经元之间的连接权值；Yj为神经网络的第j个输出值；E为输出值的均方误差；xi为神经网络的第i个输入值；yj为第j个网络输入所对应的真实值；bj为输出层第j个神经元上的偏置；rh为隐含层第h个神经元上的偏置。由于Sigmiod 函数能解决所有非线性问题，并且求导简单，还可以模拟任意决策面，故将功能神经元上的非线性函数均设为Sigmiod函数，记为f。

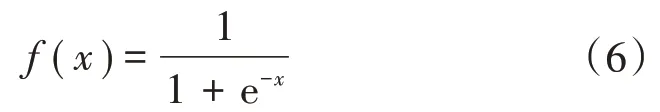
网络参数更新一般式为

根据梯度下降法，网络参数的误差求解为：

将式（8）、式（9）代入式（7），则：

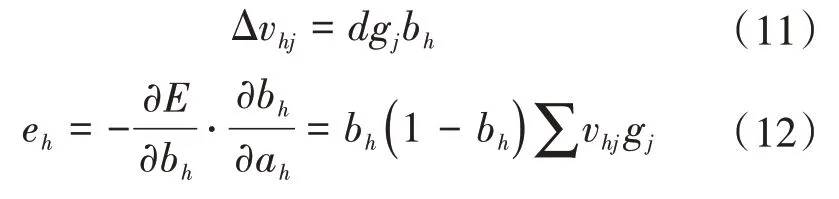
式中：gj为输出层第j个神经元的梯度；d为学习率；eh为隐含层第h个神经元的梯度。Δvhj为参数vhj的更新误差。同理得到网络其他参数的误差为

式中：Δwih、Δbj、Δrh分别为参数wih、bj、rh的更新误差。

1.2 训练基本流程

误差逆传播算法的基本过程如图3所示。

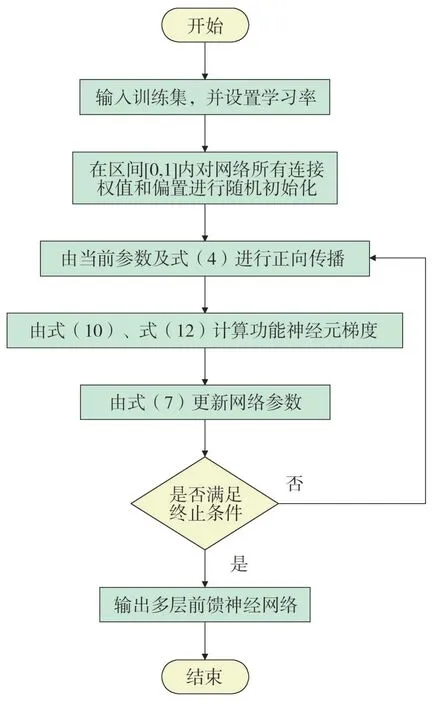
图3 误差逆传播算法流程

为避免参数频率更新过高，采用累积BP 算法，达到最小化训练集上的累积误差后更新网络参数为

式中：Ea为训练集整体的累积误差；m为训练集上的样本个数；Ei为单个样例上的均方误差。

2 鲸鱼群优化算法

BP 神经网络具有强大的非线性映射能力，多个基本单元可扩展为复杂的非线性函数，然而由于BP神经网络初始参数的随机性，训练后的网络往往陷入局部极值，基于此，结合WOA 优化算法来提升网络全局搜索能力。WOA 是一种基于种群的自然启发式算法，通过模仿座头鲸捕猎方式来解决优化问题。座头鲸是一种高智商的动物，在捕猎时，会相互合作，不断追逐并围捕猎物。在该算法中，鲸鱼的位置可以看作一种可行解。WOA 算法有着概念简单，易于实现，可绕过局部极值等优点［16］。该算法主要包括2个方面：搜索猎物行为、环绕或攻击猎物行为［17］。

2.1 搜索猎物行为

座头鲸会根据鲸鱼群中个体的相互位置随机进行搜索猎物，数学模型为：

式中：t为迭代次数；Xr（t）为迭代次数为t时，随机某只鲸鱼的位置向量；Xi（t）为当前鲸鱼i的位置向量；D1为待求解个体与随机鲸鱼的距离向量；A为收敛系数，C为摆动因子，计算公式如式（17）—式（19）所示。

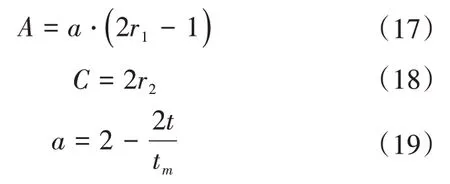
式中：tm为设定的最大迭代次数；r1和r2为区间［0，1］中的随机值；a为线性收敛因子，在迭代过程中从2线性减小到0。

2.2 环绕或攻击猎物行为

座头鲸可以识别并环绕猎物，假设当前的最优候选解为目标猎物，鲸鱼距离猎物最近的位置会影响其他鲸鱼的行动，其他鲸鱼会靠近最优鲸鱼，此模型反映鲸鱼群正朝着最佳位置移动，可以看作围绕局部最优解进行搜索，位置更新模型为

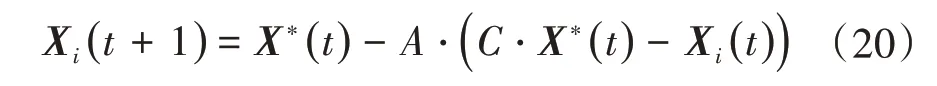
式中：X*（t）为迭代次数为t时，鲸鱼距离猎物最近的位置向量；要说明的是，如果存在更优解，则应在每次迭代中更新X*（t）。

当WOA 算法处于环绕猎物行为时，无法确定此时是否为最优位置，在此增加判断机制，当|A|≤1 时，鲸鱼群环绕猎物，当|A|＞1 时，随机选择某只鲸鱼的位置作为参考，从而更新其他鲸鱼的位置，这是为了将鲸鱼种群转移到全局范围进行搜索［18］。

座头鲸在攻击猎物时，有其独特的攻击路径，即通过泡泡网式螺旋运动行为攻击猎物，数学表达式为：

式中：b为对数螺旋形状常数，通常取为1；l为区间［-1，1］内的随机数；D2为当前状态下得到的最佳解。

值得注意的是，座头鲸在猎物周围移动时，会形成缩小的环绕圈并同时沿螺旋状路径移动，为描述这种同时发生的行为，引入概率p，假设鲸鱼群选择环绕猎物行为还是螺旋式攻击猎物行为取决于p值的大小，猎物行为表达式为

式中：p是区间［0，1］中的随机值。

WOA 算法的全局搜索能力取决于A的值，而A主要依赖于a的大小，当a取值较大时，算法具有较强的全局搜索能力，但局部寻优能力较弱，导致收敛速度下降，换句话说，a的大小对算法的收敛速度与精度有着重大影响，而传统WOA 算法中的a值在迭代过程中从2 线性减小到0，不能完全准确的反应复杂情况下的非线性搜索，针对此问题，本文引入改进后的非线性收敛因子，迭代更新式为

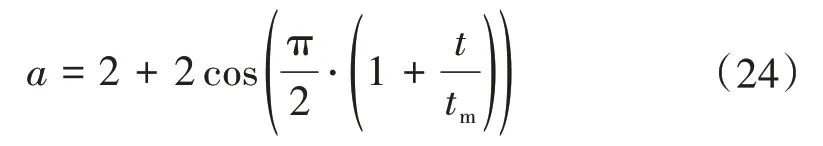
在迭代过程前期，a的非线性下降直接影响A的值，使得A≤1 以及鲸鱼群围绕猎物的概率更大，因此收敛速度得以提高。改进后的WOA 算法流程如图4所示。

图4 WOA优化算法流程

3 WOA-BP预测模型

基于WOA-BP的神经网络预测基本步骤为：

1）初始化BP 神经网络的权值和偏置，并读取数据；

2）将数据集划分为训练集和测试集，为最大效率利用数据，采用交叉验证的方法；

3）输入数据的归一化处理，区间范围为［0，1］；

4）采用经验公式确定隐含层节点个数；

5）计算鲸鱼群优化算法的决策变量长度，选取均方误差作为优化的目标函数；

6）设置算法停止标准，得到鲸鱼群优化算法优化后的神经网络的权值和偏置参数；

7）将优化得到的权值和偏置参数赋予BP 神经网络，得到WOA-BP神经网络模型；

8）进行网络训练和测试。

WOA-BP神经网络算法流程如图5所示。

图5 WOA-BP神经网络算法流程

鲸鱼群优化算法的适应度函数设计为全样本集整体的均方误差MSE，适应度函数值越小，表明训练越准确，且模型的预测精度更高。

式中：F为适应度函数值；K为预测样本的个数；Tr、Te分别为样本的训练集和测试集；MSE，Tr，Te为样本的均方误差。

而网络隐含层节点个数的确定采用经验公式为

式中：N为隐含层节点的个数；Ni、No分别为输入层和输出层的神经元的个数；a取值一般为区间［0，10］中的整数。

为了使样本数据限制在一定范围内并加快算法收敛速度，需将输入数据进行归一化［20］，公式为

式中：xni为原始样本数据xi归一化后的值；xmin为原始数据中的最小值；xmax为原始数据中的最大值。

4 试验结果与分析

4.1 试验平台

中央处理器为英特尔i5-11400H，基准频率2.7 GHz，独显为英伟达GDDR6-RTX3050，DDR4-16 GB 双通道内存，频率3 200 MHz，支持NVMe 协议的固态硬盘512 GB，Windows10 系统，仿真软件为Matlab2020a，采用以欧姆内阻定义的SOH 值作为模型输出，以基于改进的WOA-BP 神经网络模型进行在线估计SOH。

4.2 试验数据

采用马里兰大学CALCE 官网所提供的锂离子电池试验老化数据进行仿真分析［19］，选取其中锂离子电池的循环充放电次数、循环充放电再静置后的电池端电压及电流、累积充电容量、累积放电容量、循环充电时间、循环放电时间共计7 个指标作为网络输入，而以欧姆内阻值定义的SOH 作为网络输出。

试验样本为CX2型电池老化数据，以标准恒流恒压充放电协议循环试验，恒流倍率为0.5C，待电压达到4.2 V后，维持恒压状态，直到充电电流降至0.05 A以下为满电，再以1C 倍率放电，放电截止电压为2.7 V。

参数设置为网络的学习率设置为0.01，训练次数设置为1 000，WOA 最大进化迭代数为50，初始种群规模设置为30，训练目标最小误差设置为0.000 1。

为了检验本文所提估算SOH 方法的有效性，以公开的编号为CX2-35、CX2-36、CX2-37 3组锂离子电池试验老化数据分别进行测试，并以传统BP 神经网络、基于WOA-BP 神经网络以及基于种群的优化算法中常用的粒子群算法优化的BP 神经网络3种估算方法进行试验对比，为降低随机性对各种算法的影响，对每种方法进行多次试验并对输出结果取平均值，使模型趋于真实表现。另外，本文采用平均绝对误差MAE、均方根误差RMSE、平均绝对百分比误差MAPE以及运行时间等指标进行定量描述算法性能。

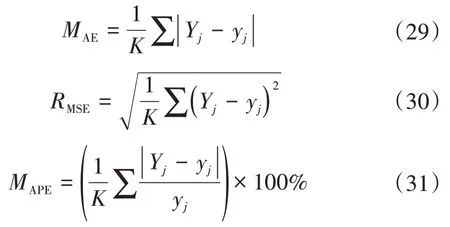
4.3 结果分析

首先通过3 组锂离子电池老化数据的测试集针对隐含层功能神，对于CX2-35 组电池老化数据而言，隐含层节点数最佳值为7；同理，CX2-36 组数据最佳隐含层节点数也为7；而CX2-37 组数据最佳隐含层层数则为5。

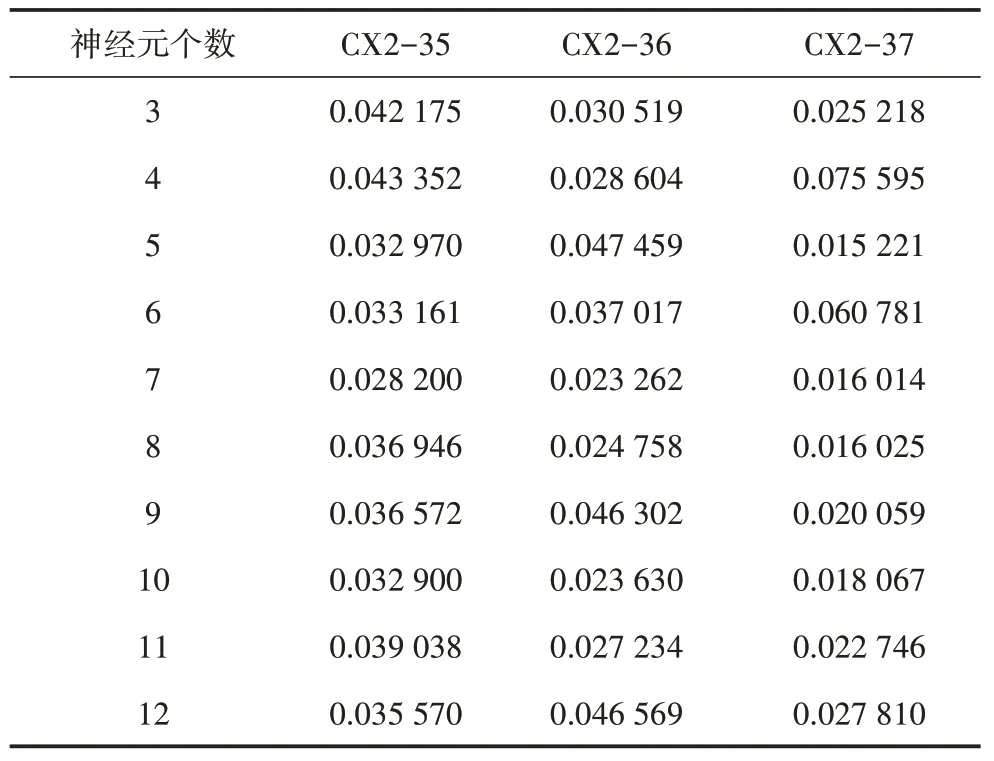
表1 隐含层神经元个数性能对比

设置网络隐含层节点个数，分别使用性能最强的隐含层层数针对3 组电池数据测试集使用上述3种方法进行训练，随机抽取测试集进行预测输出，为直观对比算法性能，对输出误差取绝对值，试验结果如图6—图8所示。

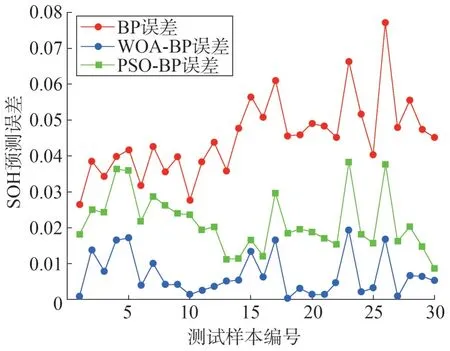
图6 CX2-35电池老化数据对比结果

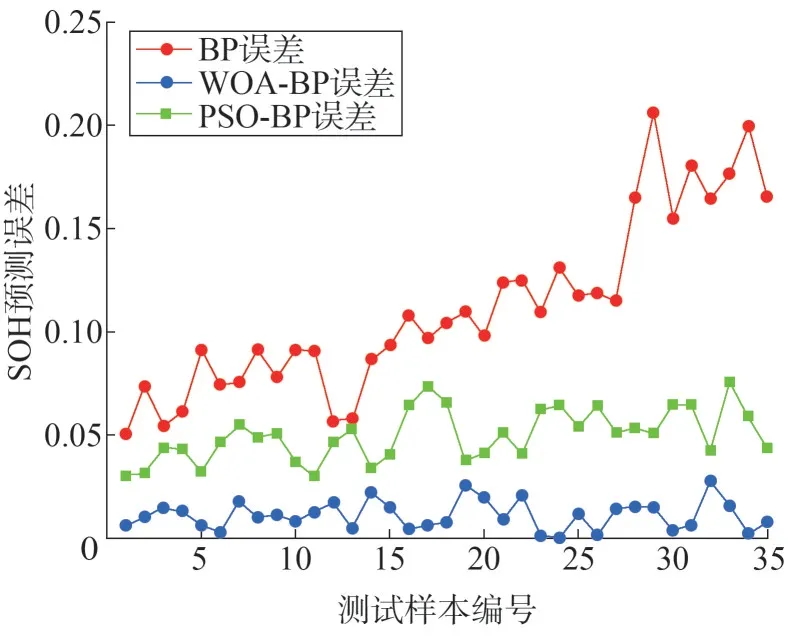
图7 CX2-36电池老化数据对比结果

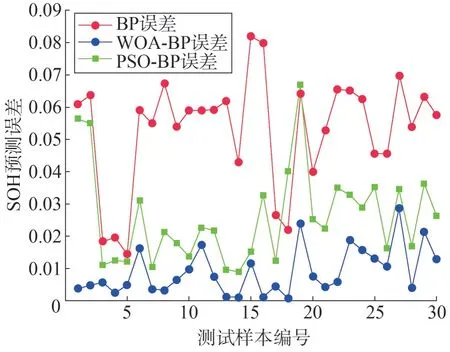
图8 CX2-37电池老化数据对比结果

通过图6 的对比结果可以发现，BP 神经网络算法预测误差最大值为0.077，最小值为0.027；基于PSO 优化的BP 神经网络算法预测误差最大值为0.038，最小值为0.008；而基于WOA 优化的BP 神经网络算法预测误差最大值为0.019，最小值为0.001。图7结果中，BP算法预测误差最大值、最小值分别为0.206、0.051；PSO-BP 算法预测误差最大值、最小值分别为0.176、0.091；而WOA-BP 算法预测误差最大值、最小值分别为0.027、0.000 3。图8 中，BP 算法预测误差最大值、最小值分别为0.082、0.015；PSO-BP算法预测误差最大值、最小值分别为0.056、0.009；而WOA-BP 算法预测误差最大值。最小值分别为0.004、0.000 8。由此可见基于WOA优化后的BP神经网络进一步提高了预测精度。3种算法的性能评价指标结果如表2所示。

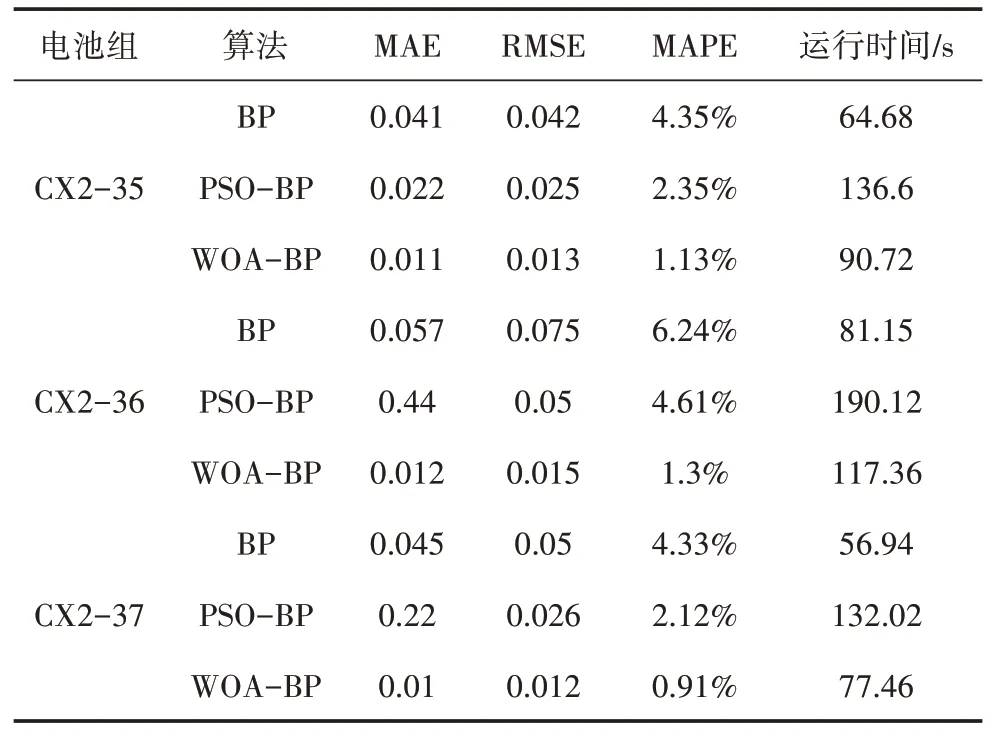
表2 各算法性能评价结果

从表2可以看出，对3组锂离子电池老化数据集测试，WOA-BP 算法相比于BP 算法以及PSO-BP 算法，在整体样本集上的平均绝对误差、均方根误差、平均绝对百分比误差等指标更优。

运行时间上，在当前试验条件下，WOA-BP 算法在CX2-35、CX2-36、CX2-37 组电池数据上相较于PSO-BP算法耗时分别缩短了33.6%、38.27%、41.3%，提高了收敛速度，具有较好的性能。

5 结语

提出了一种基于鲸鱼群算法优化的BP 神经网络来实现锂离子电池健康状态估算的方法，由于锂离子电池健康状态无法直接测量，且具有非线性及波动性，该方法绕开直接模拟电池内部复杂的物理化学反应，通过BP 神经网络进行非线性映射。针对传统BP 算法初始参数随机化易陷入局部极值的问题，利用改进的WOA 算法对网络初始参数全局寻优并进行训练，在马里兰大学公开的试验数据集上进行验证分析，结果表明，本文提出的鲸鱼群算法优化的BP 神经网络在锂离子电池健康状态估算上相比传统BP 算法、PSO-BP 算法性能更优，预测精度更高，收敛速度更快，效果更好。

由于本文并未考虑锂离子电池随机充放电、不同倍率充放电、温度变化等实际运行复杂工况，下一步进行健康因子特征提取并考虑随机充放电等复杂工况下提高算法的预测性能及泛化能力。