面向铁路工程三维信息重建的无人机航线规划改进方法

王凯

中国铁路设计集团有限公司，天津 300251

无人机航线规划主要有基于几何学的搜索算法和基于控制论的航迹算法。航线规划主要是为了提高规划效率，降低规划时间，提高无人机飞行作业的安全性。目前相关研究主要集中在军用领域，民用航空摄影测量的航线规划主要以传统的弓字形、井字形航带规划设计为主，面向铁路应用场景的无人机航线规划研究较少。

我国铁路运营总里程已达到15万km，高速铁路运营里程已达到4万km。随着铁路建设的高速增长和铁路数字化建设、智能化运营转换，需要高精度铁路实景模型作为铁路智慧化建设、运维基础三维数据场景［1］。铁路工程建设、既有线高精度实景模型重建所需的无人机数据采集一直存在瓶颈问题。在狭小带状区域获取数据的角度较少，无人机在铁路正上方和反复穿越既有线航飞作业存在巨大的安全隐患。按照传统无人机三维实景重建航线规划方法，需要采用弓字形、井字形飞行，无法避免以上问题［2］。普通三维实景无人机航飞数据获取方法无法做到面向铁路针对性的多角度定制采集，铁路三维模型重建精度、效率低。

本文针对铁路高精度实景重建数据采集现状，提出一种面向铁路工程三维信息重建的无人机航线规划改进方法。相比传统井字形、弓字形航线（图1），改进方法采用单侧回旋多角度飞行作业采集（图2），运用优视摄影测量原理，有效避免无人机在铁路正上方和交叉穿越铁路运营线作业，提高数据采集的针对性、数据重建的效率和模型的精细化程度，实现铁路运营天窗时间内高效地开展无人机多角度数据采集，为铁路智慧化建设和运营提供精确的实景三维场景。

图1 传统井字形航线规划

图2 回旋多角度数据采集航线规划

1 铁路中线节点加密

铁路数字中线一般只记录线段折线节点坐标，对长距离的直线段中间区域无坐标记录。为了按照一定距离均匀布设航点，需要进行铁路中线节点加密。

利用既有铁路中线资料进行铁路中线节点坐标加密。利用相机参数（像元尺寸为p，画幅尺寸为px×py，相机镜头焦距为f）和相对航高h进行物方覆盖的地表区域尺寸计算［3］。所覆盖的地表区域尺寸Lx、Ly与相对航高关系［4］为

对于回旋多角度的数据采集，其地面投影区域的形状如图3所示。其核心有效投影区域（高精度）为红色区域，一般区域（普通精度）为黄色区域。核心区域形状可以抽象为圆形，直径长度为Lx。一般区域的形状也近似为圆形，直径长度为Ly。对于一条航带，相邻核心区域两两重叠，其重叠率r为重叠区域面积Soverlap与两个圆形面积总和Scircular的比值［5］。对于图4，L x为核心区直径；D为两个圆心距离的1∕2；L为对应弦长

图3 影像地面投影区域

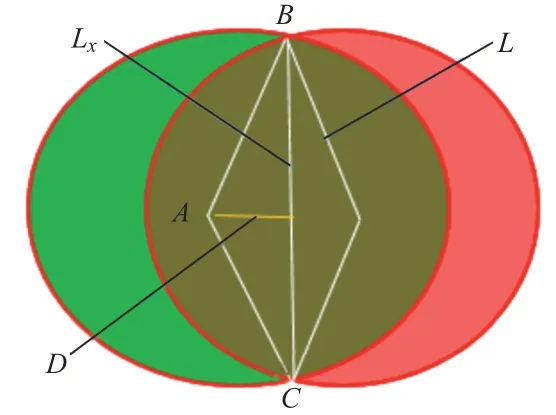
图4 核心区域重叠率的计算

以A点为圆心、为弧长的对应圆心角α的计算式为

扇形A BC的面积SH，A BC计算式为

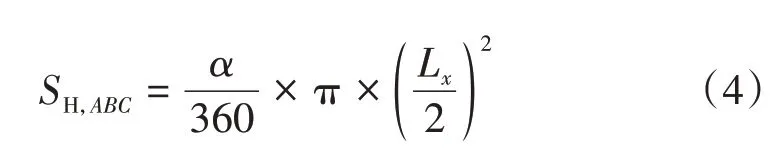
三角形AB C的面积ST，ABC计算式为

重叠区域面积Soverlap计算式为

重叠率r计算式为

由式（3）—式（7）建立了r与D的对应关系，利用r与Lx可实现加密点间隔D的计算［6］。已知铁路中线节点坐标为（Loni，Lati），i=1，2，…，m。对（L oni，Lati）与（Loni+1，L ati+1）之间的坐标进行内插，内插坐标为（L on j，Latj），j的取值为0～n［7-8］。n的计算式为

内插坐标（Lonj，L atj）的计算式为

得到加密后的中心节点地理坐标数组（loni，l ati），i的取值为

2 外扩安全缓冲区的计算

以加密的铁路中线节点为基准，计算安全缓冲区边界。将加密后的坐标（l oni，lati）垂直于中线左右分别外扩距离Dbuffer，并计算外扩后的坐标（l onL，latL）、（lonR，l atR），效果见图5。

图5 安全区边界节点坐标计算

具体的实现方式如下：

①将加密后的中线节点地理坐标（l onL，i，latL，i）转换成大地空间平面坐标（XR，i，YR，i），其转换方法为通用方法［9］。

②利用（Xi，Yi）、（Xi+1，Yi+1）坐标计算两个点坐标方位角θ［10］，计算式为其中

对于左侧外扩的区域，航向角向左旋转90°得到旋转后的坐标方位角θL［11］，计算式为

当θ-90°≤-180°时

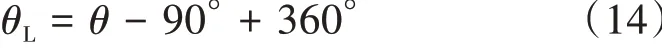
当-180°＜θ-90°＜180°时

③将（Xi，Yi）向左平移Dbuffer得到向左外扩后平面坐标（XL，i，YL，）i，其计算式见式（16）、式（17），同理得到右侧的坐标（XR，i，YR，）i。

④将外扩节点平面坐标转（XL，i，YL，i）、（XR，i，YR，i）转换为外扩节点地理坐标（LonL，i，LatL，i）、（L onR，i，L atR，i）。

3 曝光点参数计算

3.1 曝光点坐标和相对航高计算

以安全区边界节点地理坐标（L onLi，LatLi）、（LonRi，L atRi）为基准进行多角度曝光点位置计算，见图6。

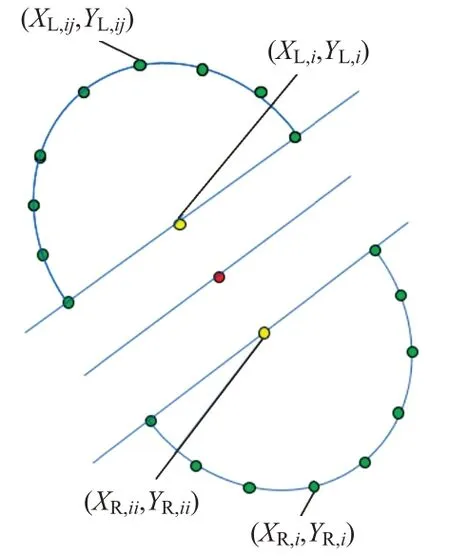
图6 曝光点坐标计算

1）（LonL，i，LatL，i）、（LonR，i，LatR，i）地理坐标转化为平面投影坐标（XL，i，YL，i）、（XL，i+1，YL，i+1）。（XL，i，YL，i）、（XL，i+1，YL，i+1）坐标是由（Xi，Yi）、（Xi+1，Yi+1）向左平行计算所得，因此二者的坐标方位角θL与（Xi，Yi）、（Xi+1，Yi+1）坐标方位角θ相等［12］。

2）对于左侧外扩的区域，航向角θL逆时针依次旋转20°、40°、60°、80°、100°、120°、140°、160°、180°，经过多次试验论证，旋转角度间隔、数据量与模型精细化程度上存在最优的关系，根据经验值得到角度为20°。旋转后的坐标方位角θLi，i取值为1～9，即

当θ-20°i＜-180°时

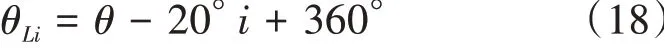
当-180°＜θ-20°i＜180°时

对于右侧外扩的区域，航向角顺时针向依次旋转0°、20°、40°、60°、80°、100°、120°、140°、160°、180°。旋转后的坐标方位角θRi，i的取值为1～9，即

当θ+20°i＞180°时

当180°＜θ+20°i≤180°时

利用平面坐标（LonL，i，LatL，i），按照（h-Dbuffer）为半径计算曝光点的平面坐标（XL，ij，YL，ij），其中Dbuffer为缓冲区距离，j取值为1～9，计算式［13］为

3）将曝光点平面坐标（XL，i j，YL，ij）、（XR，ij，YR，ij）转换为曝光点地理坐标（L onL，ij，L atL，i j）、（LonR，ij，L atR，ij）。

4）利用（LonL，ij，LatL，ij）、（L onR，ij，L atR，ij）提取基础数字地形模型高程ZL，ij、ZR，ij，以第一个点的高程绝对值ZL11、ZR11为基准计算相对高程值HLij、HRij，计算式［14］为

曝光点航飞仿地相对高度值Sij计算式［15］为

3.2 曝光点云台方位角、俯仰角计算

1）航向角计算

利用曝光点坐标（L onL，ij，L atL，ij）、（L onR，ij，LatR，ij）与线路中心加密节点坐标（loni，lati）进行无人机云台方位角ψij（两坐标的坐标方位角）计算，相关效果见图7。

图7 曝光点云台方位角计算

ψij计算式为

其中

2）俯仰角计算

根据各个曝光点投影坐标（XL，ij，YL，i j）、（XR，ij，YR，ij）与对应铁路既有线中线加密节点投影坐标（xi，yi）和设定的相对航高h进行云台俯仰角ρij拍摄的计算［16］。

4 航线规划软件与实景三维重建试验

4.1 航线规划软件

根据以上航线规划算法进行航线规划地面站软件设计与开发。通过人机交互的方式圈划铁路中线或导入铁路中线矢量文件［17-19］，并设置相应的相机参数、相对航高、安全缓冲距离等进行曝光点位置、参数与航线参数的自动计算，生成可执行的航线任务文件。任务文件可直接导入无人机平台，无需编辑即可开展全自动作业。

4.2 无人机数据采集与三维重建试验

选择朝凌高速铁路开展算法应用对比试验。选择含有隧道出口、桥梁、路堑边坡的6 km路段作为试验段，覆盖铁路主体工程（中线两侧各50 m范围）。采用焦距56 mm，4 100万单镜头相机。传统井字形算法采用航向80%，旁向80%的重叠率，本算法同样采用80%重叠率。对试验数据获取情况与三维重建效率进行统计分析，见表1。可知：本文算法所需获取的数据量比传统算法减少21%，观测角度为传统观测的3.6倍，重建时间缩短21%。

表1 本文算法与传统方法对比

通过影像空三加密、模型表面三角网构建、模型表面纹理贴图等工作，隧道洞口、轨道等目标得到精细化的重建，具体效果见图8。相比传统井字形数据获取模型的重建效果（图9），模型的精细度程度得到明显提升。

图8 本文方法轨道重建效果

图9 传统井字形轨道重建效果

5 结论

1）使用无人机回旋多角度航线规划方法能有效实现铁路工程目标三维重建航飞作业任务规划，与传统单镜头井字五向航飞采集方式相比，有效减少了获取数据的冗余度，提高了实景模型重建的效率。

2）采用建立安全缓冲区方式开展航飞作业，避免了无人机作业过程中的线路交叉穿越，提高了数据采集的安全性。

3）使用回旋多角度方法进行数据采集，使得目标的观测角度更多，减低了数据获取的盲区，减少了模型的拉花现象，提高了模型重建的精细化水平。