中国与西非桥梁设计洪水计算方法的比较分析

周马生 齐梅兰 高洪岩 曾险 马晓东

1.中国路桥工程有限责任公司，北京 100011；2.北京交通大学土木建筑工程学院，北京 100044

我国铁路及公路建造技术在“一带一路”国家特别是在非洲交通建设中发挥着巨大作用。交通线路上的桥涵设计既要满足流域排水和水资源保护的需求，也要保证桥涵泄洪时的安全。设计洪水的大小和准确性对桥涵设计至关重要，所以设计洪水的理论及计算方法在非洲受到特别关注。

从对1984年中国宝成（宝鸡—成都）铁路桥梁水害的分析中已充分认识到，设计洪水的不确定性会影响到桥涵泄洪安全。然而，对桥涵设计洪水的研究相对较少，特别是在缺乏水文实测资料的小流域地区，设计洪水流量的计算十分困难。早在1995年就有学者分析了中国多座铁路桥的水害原因后提出，应努力探索桥梁设计洪水尤其是小流域暴雨洪峰流量的计算方法［1］。暴雨和洪水属于随机水文事件。根据水文实测资料，设计洪水流量计算有两大类方法：①实测年最大洪水流量资料足够多时，可直接采用频率分析法［2］；②仅有年最大降雨量资料时，采用设计暴雨推算设计洪水流量［3-5］。设计暴雨通常由对降雨量样本的频率分析得到。

在西非以及中国的小流域地区，实测洪水流量资料十分缺乏，桥涵设计洪水流量多由第②类方法推算。受气候、地理、土壤、植被等各类因素影响，各地的降雨特征及降雨量分布不尽相同，设计暴雨的频率分析、计算设计洪水流量的公式及其参数也各不相同［6］，应用时需要深入研究和分析。本文就中国与西非常用的频率分析方法和设计洪水流量推算方法进行对比分析，以西非科特迪瓦高速公路桥为例，对各种方法的适用性进行验证，讨论分析计算结果的合理性。本研究对西非地区和中国小流域桥涵设计洪水流量的计算具有参考意义。

1 频率分析

水文频率分析就是用年最大值法选取实测资料样本，先计算其经验频率，再用理论频率分布对其进行模拟，得到理论频率分布特征值，以此推求水文变量的设计值。

1.1 经验频率计算

对样本的经验频率计算，中国用数学期望公式，西非则采用根据概率的古典定义得出的公式［7］。虽然由两种公式计算的样本平均值误差相当，但对于有限样本降序排列中的末项，由西非所采用的公式计算的频率为100%，这样的结果显然是不合理的。

1.2 理论频率分布

理论频率的分布线型有数十种之多，需要根据区域水文特点选用合适的线型。

既有研究［3，8］认为，中国河流的洪水发生频率大多能较好符合皮尔逊Ⅲ（P-Ⅲ）型分布。该分布的累积概率函数F(x≥x P)为

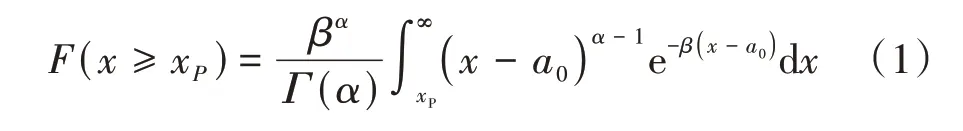
式中：x为水文变量；x P为水文变量取值，下角标P为频率；Γ（α）为伽玛函数；α、β、a0分别为P-Ⅲ分布的形状、尺度和位置参数。

对式（1）取变量代换后，有

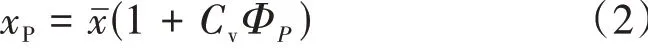
式中：xˉ为样本均值；Cv为变差系数；ΦP为离均系数。

在西非对水文频率分布线型尚没有统一认识，常选用正态（Normal）、耿贝尔（Gumbel）等分布线型。其中由Gumbel分布线型得到的水文设计值相对偏于安全，故本文仅将其与P-Ⅲ分布线型作比较分析。Gumbel分布函数［9］F（x）表达式为

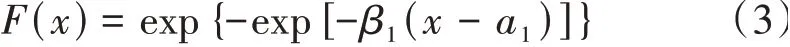
式中：β1和a1分别为Gumbel分布的尺度和位置参数。

基于该分布，有［10］

式中：K P为对应于P的分配系数；σ为标准差。

各种频率分布线型对于实测样本经验频率分布拟合的优度可采用Kolmogorov-Smirnov（K-S）、Anderson-Darling（A-D）等方法进行检验。

2 设计洪水流量推算方法

根据降雨资料推算设计洪水流量的方法有很多，其中推理公式法是比较基础的方法，其表达式为［3-4］

式中：Qm，P为设计洪水流量，m3∕s；α2为径流系数；i为平均净雨量，mm∕h；A为流域面积，km2。

推理公式法的基本假设是降雨与由其形成的洪水同频率。

按推理公式法推算Qm，P时，需要基于产流-汇流原理先进行产流计算，即根据时段Δt的设计暴雨量HΔt，P求出i，再通过汇流计算得到Qm，P。对于复杂的产流-汇流计算，根据式（5）可推演出不同的设计洪水流量计算公式。在中国小流域和西非地区常分别采用中国水科院方法和ORSTOM方法推演的公式。下面对这两种方法进行对比。

2.1 中国水科院方法

中国水科院方法按照产流历时tc和汇流时间τ的关系，从式（5）推演出

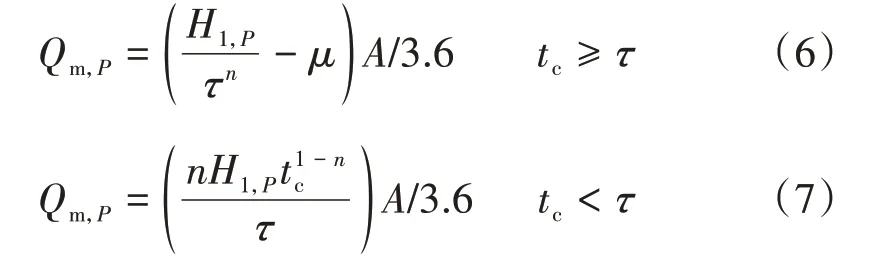
式中：H1，P为Δt=1 h的设计暴雨量，mm；μ为降雨损失量，mm；n为暴雨衰减参数。

式（6）和式（7）分别称为全面汇流模式和部分汇流模式。由式（6）或式（7）计算Qm，P时，需补充三点［3］：其中：L为流域长度；w为汇流参数，按文献［3］计算；J为流域坡度。HΔt，P通过对实测各年最大Δt时段雨量HΔt的频率分析得到。

2.2 西非ORSTOM法

西非在计算Qm，P时，首先求P=10%时的设计洪水流量Qm，10%，然后计算P＜10%时的Qm，P。计算公式为［7］

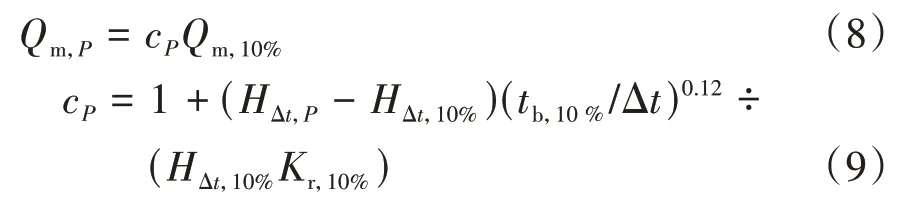
式中：c P为比例系数；tb，10%为径流总历时，h；Kr，10%为径流系数。

在西非计算Qm，10%的方法有多种，其中ORSTOM法适用于面积较大流域，应用较广泛。ORSTOM法的计算公式为［11］

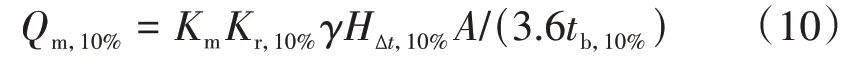
式中：Km为峰值系数；γ为将观测点雨量换算为流域平均雨量的衰减系数。

根据式（10）各参数的物理意义可知，该公式体现了由降雨到产流-汇流的原理，是对式（5）的推演和具体表达。关于ORSTOM法的汇流模式是按全面汇流考虑的。

采用ORSTOM法推算Qm，P时，HΔt，10%通过对HΔt进行频率分析得到，Km从经验数据表［11］取值，Kr，10%和tb，10%与流域面积、土壤透水性（分为B1—B5）、流域坡度（分为R1—R6）、植被覆盖度等有关。在A≤120 km2范围内，文献［11］给出了热带植被、B3类土壤和不同坡度时Kr，10%和tb，10%随A变化曲线，分别见图1和图2。

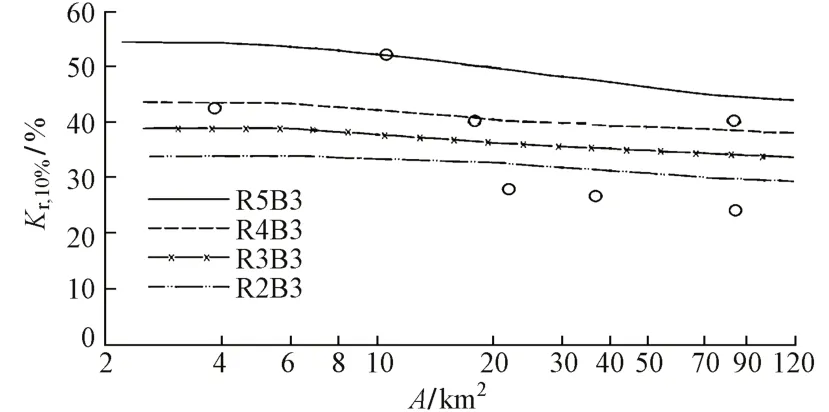
图1 B3土壤和不同坡度下K r，10%随A变化曲线

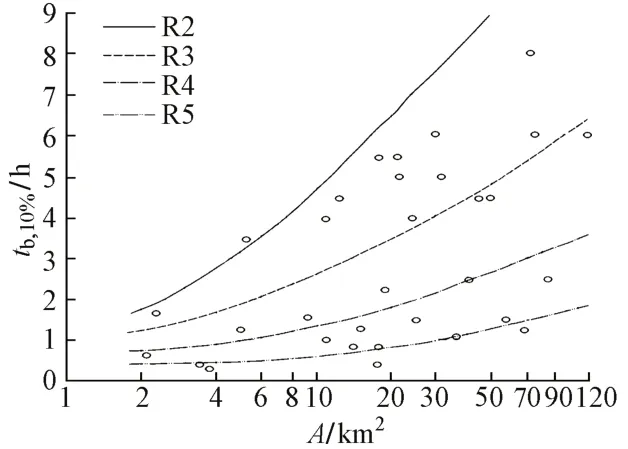
图2 不同坡度下t b，10%随A变化曲线

对图1中R3B3曲线拟合得到

（1）高校教师数据意识与态度。在所调查的样本中，内蒙古17 所本科高校中教师使用数据解决问题的意识中，36.7%的教师数据意识较强；33.3%的教师对于数据意识没有概念，也从不留意身边数据；其余30%的高校教师偶尔关注周边数据，并将其应用教学实例中。在数据态度方面，考察教师使用数据的伦理道德方面，是否合理、安全地使用数据，并对所含隐私数据是否进行保护等方面，其中83.3%的高校教师选择从合法渠道买卖数据并保护隐私数据。

同理，对图2中R3曲线拟合得到

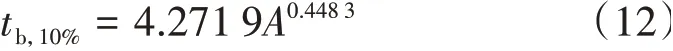
根据文献［11］的已有数据拟合得到

式（11）—式（13）中各参数与A的相关系数分别为0.97、0.99和0.99，表明相关性很好，可用于计算A＞120 km2流域的Kr，10%、tb，10%和γ。

3 工程应用

拟建高速公路桥位于西非科特迪瓦，设计时需要求取该桥的设计洪水流量。根据西非桥梁的设计洪水标准按洪水重现期100年［4］或P=1%进行设计。该地区为半湿润热带气候，多年平均年降雨量1 013.68 mm。公路桥所在流域地形呈窄长状（图3），J=1.63‰，L=72.10 km，A=1 162.05 km2。

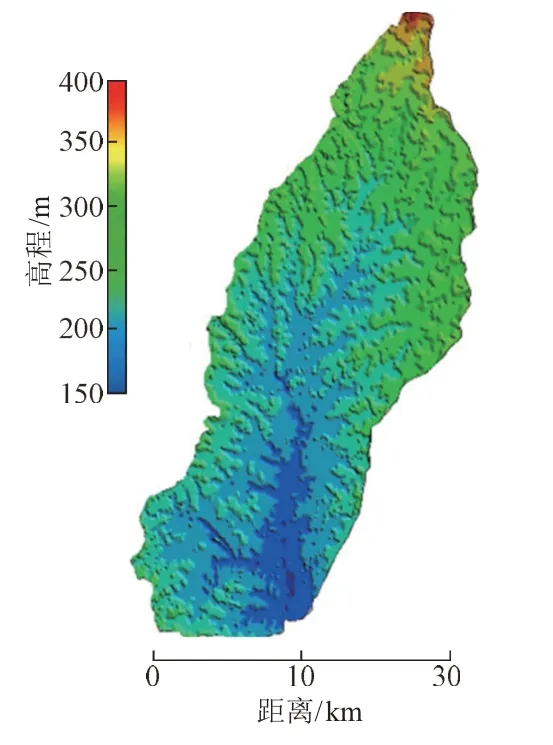
图3 流域地形

流域内植被覆盖少，符合热带特征，土壤主要由砂砾和砂性土组成。收集了该流域1960—1998年间各年最大的Δt=24 h降雨量H24，见表1。

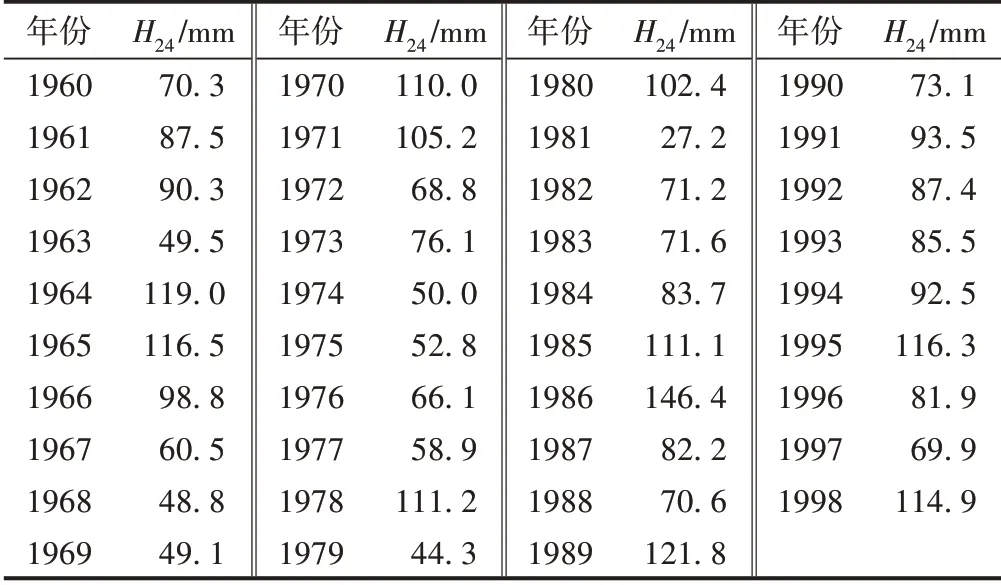
表1 各年H24实测数据

根据上述资料先采用多种频率分布线型进行降雨量频率分析，得到该流域设计暴雨量H24，1%，再采用中国和西非方法计算该桥的设计洪水流量Qm，1%，并进行比较分析。

3.1 降雨量的频率分析

P-Ⅲ分布的ˉH24和Cv值采用上述估计值，偏态系数Cs用适线法确定，这里假定Cs=（2-4）Cv，进行多次优化配线。根据ΦP表［3］和式（2）计算不同频率下H24值。将样本的经验频率分布和取不同Cs值得到的P-Ⅲ分布曲线绘入图4，采用目估适线法进行最佳配合曲线判别。比较可知：Cs=3Cv时P-Ⅲ分布与经验频率分布更接近，故该Cs值可作为本流域P-Ⅲ分布的最佳参数估计值。由此分布曲线可得H24，1%=161.66 mm。

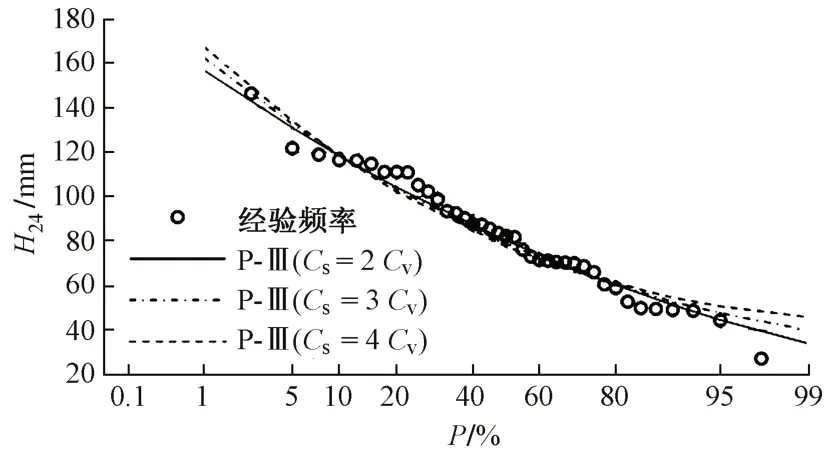
图4 H24的P-Ⅲ分布和经验频率分布对比

Gumbel分布的参数根据本流域样本条件计算得到β1=0.05，a1=71.16 mm。查K p表［10］和采用式（4）求出各频率的H24，可绘出频率分布曲线。Gumbel分布与经验频率分布对比见图5。可知，两种分布在P＞50%的区域吻合较好，在P＜10%的区域Gumbel分布的H24有偏大趋势。从Gumbel分布得到H24，1%=176.84 mm。

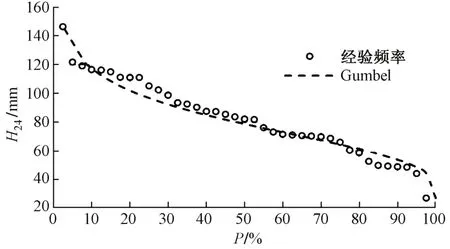
图5 H24的Gumbel分布与经验频率分布对比

为了增加H24，1%计算结果的可靠性，采用Normal分布进行降雨量频率分布模拟，计算过程不再赘述。由Normal分布可得H24，1%=144.42 mm。

采用K-S检验法对以上得出的P-Ⅲ（Cs=3Cv）、Gumbel和Normal分布线型进行优度检验，选出与样本的经验频率分布拟合最优者。计算各理论频率分布与经验频率分布的最大绝对离差Dmax，将其与置信度95%水平的检验临界值p、检验结果以及由各分布线型得到的H24，1%值列于表2。其中各种频率分布线型均满足Dmax＜p，故均能通过检验。比较各分布线型Dmax和H24，1%可知：虽然Normal分布线型的Dmax值最小，但该分布所得H24，1%较其他分布也明显偏小，对于工程设计来说偏于不安全；Gumbel分布线型的Dmax值小于P-Ⅲ分布线型，表明其拟合度更优，且H24，1%较大，对工程设计偏于安全。故采用由Gumbel分布线型得到的

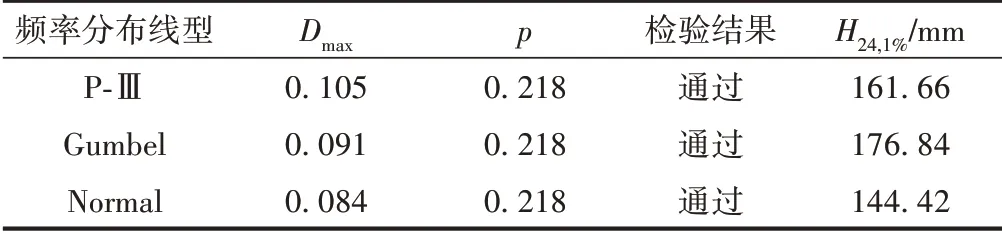
表2 拟合优度检验和设计暴雨量

H24，1%=176.84 mm。

从Gumbel分布线型得到H24，10%=122.55 mm，此值用于ORSTOM法计算设计洪水流量。

3.2 设计洪水流量

中国水科院方法推演的公式中各参数根据本工程案例的流域资料得到。其中n=0.65，H1，1%=53.15 mm，由经验公式［12］可得μ=4.59 mm∕h，tc=8.6 h，按文献［3］取流域特征参数θ=285，计算得到w=0.58。假定流域汇流模式为部分汇流，对式（7）和计算τ的公式进行迭代，可解得Qm，1%。当迭代至误差ε≤±3%时，得到τ=74.9 h，Qm，1%=282.60 m3∕s。此结果满足tc＜τ的部分汇流假定，故此Qm，1%值即为所求。

采用ORSTOM法计算时，识别出本流域的坡度和土壤透水率分别属于R3和B3类型，可由式（11）—式（13）计 算 有 关 参 数，得 到Kr，10%=0.31、tb，10%=101.05 h、γ=0.314，将其和Km=2.5［7］代入式（10）得到Qm，10%=95.26 m3∕s。将各参数已知值代入式（9），得c1%=2.65。最后由式（8）求得Qm，1%=252.44 m3∕s。

为了多方法比较，还采用美国Soil Conservation Service-Curve Number（SCS-CN）方法计算了Qm，1%，可参考文献［13］，不再赘述。

以上各方法计算所得的Qm，1%见表3。可知，ORSTOM法计算结果和SCS-CN法很接近，中国水科院方法的计算值偏大11.92%。大桥设计可采用ORSTOM法的结果Qm，1%=252.44 m3∕s。

表3 各方法的设计洪水流量计算结果对比

4 结论

本文主要对比了中国和西非水文频率分析常用的P-Ⅲ、Gumbel分布线型，简述了由设计暴雨量计算设计洪水流量的中国水科院方法和西非ORSTOM法并阐释了它们的物理意义，建立了ORSTOM法的参数计算方程。以西非科特迪瓦高速公路桥为例验证了各种方法的适用性，并辅以美国SCS-CN法进行多方法对比和分析。得到如下结论：

1）降雨的规律与地区气候密切相关，统计意义上P-Ⅲ和Gumbel分布线型均能较好地模拟西非地区多年雨量的频率分布，但Gumbel分布拟合更优，所得设计暴雨量偏于安全。

2）工程应用表明，ORSTOM和中国水科院方法计算设计洪水流量均能得到合理结果。ORSTOM法计算简单，且由于其中主要参数的计算方程是根据工程实例所在流域的现场观测数据拟合得到，所以各参数计算值准确性较高，所得设计洪水流量更可靠；中国水科院方法的计算结果偏大11.92%。

3）降雨与洪水是具有随机性的水文现象，由降雨形成洪水的产流-汇流机制及影响因素非常复杂，因此充分认识流域气候、下垫面特征，分析实测地表数据，用多种方法进行计算、对比和检验，对减少设计洪水计算结果的不确定性十分重要。