小净距隧道中岩墙对拉锚杆加固效果分析

王浩 杨新安

1.同济大学道路与交通工程教育部重点实验室，上海 201804；2.同济大学交通运输工程学院，上海 201804

中岩墙对小净距隧道围岩的稳定性起着决定性的作用，保证其承载能力是小净距隧道支护的关键［1-4］，对中岩墙加固措施的研究有重要意义。中岩墙加固主要有注浆、普通锚杆、对拉锚杆等方式，其中对拉锚杆是一种优势明显的加固方式，万石山隧道、金旗山隧道、石狮隧道均采用此加固方式［5-6］。

相关研究人员通过现场实测、数值计算分析了对拉锚杆的加固机理。刘艳青、黄成造等［7-8］基于围岩位移和对拉锚杆轴力变化，认为对拉锚杆受力与中岩墙变形相协调，可以有效控制围岩位移，改善支护结构受力，轴力越大加固作用越明显。黄拔洲、姚勇、刘芸、周飞等［9-13］通过数值计算表明对拉锚杆可以避免中岩墙塑性区贯通，同时改善二次衬砌受力，中岩墙力学参数越大，加固效果越好，加固软弱围岩时，预应力明显损失。上述研究成果侧重于对拉锚杆对隧道围岩稳定性的影响，未就对拉锚杆产生的水平约束和力学参数改善进行定量分析，忽略了对拉锚杆使用后中岩墙的力学特征。

本文建立对拉锚杆加固力学模型，对不同加固参数下中岩墙的力学特征进行分析，通过工程应用对加固机理进行验证。

1 水平约束计算公式

在不考虑其他支护的条件下，对拉锚杆加固方案见图1（a），简化模型见图1（b）。其中：w为中岩墙宽度；h为中岩墙高度；q为中岩墙承受荷载；Δh为垂向变形。

图1 预应力对拉锚杆加固方案及简化模型

不超出弹性极限时，中岩墙水平应变εw与垂向应变εh的关系为

式中：μ为中岩墙泊松比；εw=Δw∕w；εh=Δh∕h；Δw为水平变形，计算式为

对拉锚杆加固时，锚杆杆体与中岩墙之间空隙由注浆填充，锚杆轴向等效刚度系数Kb由锚杆杆体和注浆体决定，即

式中：Eb为杆体弹性模量；Eg为注浆体弹性模量；db为杆体直径；d为锚杆直径。

若对单根对拉锚杆施加预应力为P，则n根对拉锚杆产生的约束力F可近似表示为

式中：Δ′w为中岩墙加固后水平变形。

将式（2）、式（3）代入式（4）得到

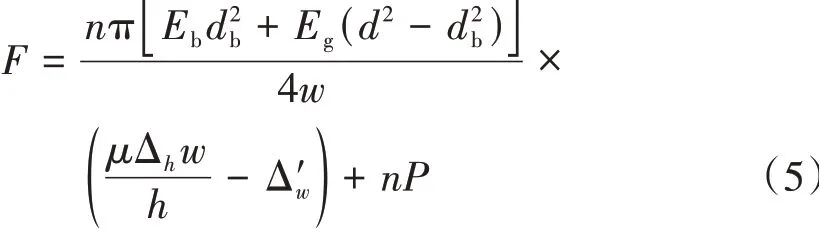
则对拉锚杆产生的水平约束σ′计算式为

式中：l为锚杆排距。

2 中岩墙力学参数

根据均匀化理论［14］，加固后中岩墙的等效力学参数由锚杆参数和中岩墙原始参数共同决定，等效材料的弹性模量可由等效公式（7）计算得到。

式中：E*、A*分别为加固后中岩墙等效强度的弹性模量和面积；E1、A1分别为锚杆的弹性模量和面积；E、A分别为未加固时中岩墙的弹性模量和面积。

E*的计算公式为

式中：E为未加固前中岩墙的弹性模量；s为锚杆间距。

均匀化后的等效材料仍服从Mohr-Coulomb强度准则，其在主应力坐标系中的屈服轨迹见图2（a）。其中：f为屈服轨迹梯度，σc为屈服轨迹截距，σc=2ccosφ∕(1-sinφ)，c为黏聚力，φ为内摩擦角。当岩体的围压较小时，岩体的强度包络线可以近似看作一条直线，见图2（b）。

图2 加固前后屈服轨迹及强度包络线

根据图2（a），强度准则表达式为

式中：σ1为最大主应力；σ3为最小主应力。

加固后屈服轨迹梯度f*与加固前关系为

式中：α为锚杆密度因子。

加固后屈服轨迹截距与加固前关系为

参考文献［15-17］中的锚杆密度参数，α的计算式为

式中：η为锚杆与中岩墙之间的摩阻系数，与锚杆表面粗糙度有关。

根据式（10）、式（11），对拉锚杆加固后中岩墙等效材料的内摩擦角φ*和黏聚力c*计算式分别为

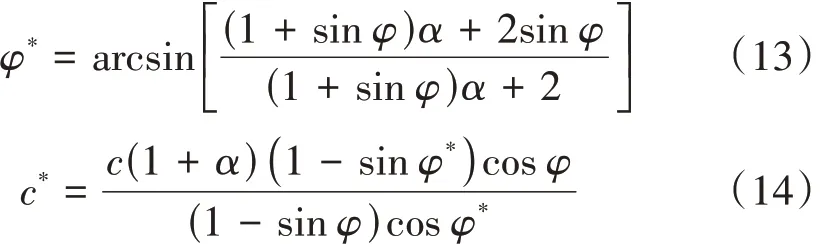
不考虑中间主应力时，对拉锚杆产生的水平约束σ′可以看作σ3，σ1可以近似认为是中岩墙在加固后的抗压强度［σc*］。将式（6）带入式（9）得加固后中岩墙抗压强度的计算式为

由式（15）可知中岩墙抗压强度主要由两个方面决定：①对拉锚杆参数；②中岩墙力学参数。

3 中岩墙力学特征

基于上述计算公式进行数值模拟分析，研究不同参数下的加固效果。

3.1 数值模型建立

京张高速铁路八达岭长城站为多层地下结构，部分设备硐室设计为小净距隧道。利用FLAC 3D软件建立数值模型，见图3。左、右和下边界约束法向位移，上边界自由。围岩使用zone单元和Mohr-Coulomb模型，对拉锚杆使用pile结构单元，模拟方法参考文献［18］。围岩力学参数见表1。

表1 围岩力学参数

图3 数值模型

为监测位移，自上而下布置垂向间距为2 m，水平间距为0.5 m的测线，如图4所示。

图4 监测点布置（单位：m）

根据式（6）和式（15），分别建立无锚杆和锚杆间排距2.0、1.0、0.5 m、预应力60 kN的计算模型，同时在间排距0.5 m、预应力60 kN的模拟中，间排距保持不变，增加预应力30、120 kN的计算工况。

3.2 计算结果分析

1）位移特征分析

中岩墙水平位移变化曲线见图5。可知：中岩墙水平位移关于中线对称，中部水平位移大于顶部和底部。无加固时，最大水平位移点位于中部，位移为9.5 mm。对拉锚杆加固后，当预应力为60 kN时，在间排距2.0、1.0、0.5 m条件下，最大水平位移分别为7.8、6.5、3.2 mm。间排距为0.5 m时，在预应力30、120 kN条件下，最大水平位移值分别为3.7、2.3 mm。

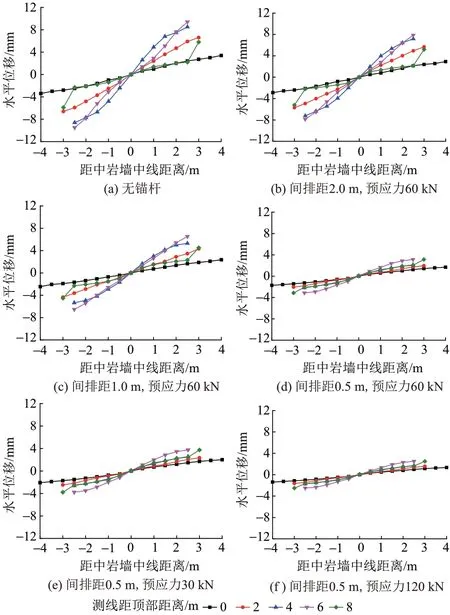
图5 中岩墙水平位移变化曲线

中岩墙竖向位移变化曲线见图6。可知：无加固时，中岩墙顶部最大竖向位移为22.3 mm，底部最大竖向位移为9.24 mm，顶部沉降值大于底部隆起值。对拉锚杆加固后，顶部沉降值和底部隆起值均减小，最大竖向位移减小至9.6 mm，同时边墙切线与中岩墙中线之间竖向位移差减小，位移曲线趋于平缓。无对拉锚杆加固时，最大位移差为4.7 mm，位于中岩墙中部，使用对拉锚杆加固后最大位移差减小到1.3 mm。

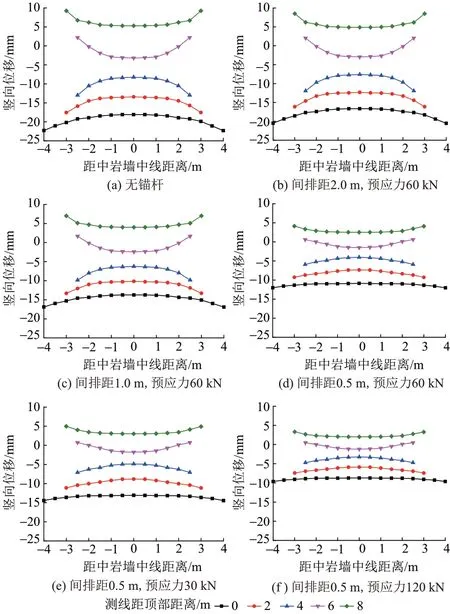
图6 中岩墙竖向位移变化曲线

综合中岩墙的位移变化可以看出，由于对拉锚杆施加了水平约束，改善了中岩墙力学参数，提高了抗压强度，阻止了位移进一步扩展，因此位移峰值和各监测点之间位移差减小。锚杆间排距越小，预应力越大，加固效果越明显。

2）应力特征分析

中岩墙最小主应力分布见图7。可知：中岩墙无加固时最小主应力σ3为1.07～2.62 MPa。加固后在预应力60 kN，间排距2.0、1.0、0.5 m条件下，σ3为1.08～2.63、1.26～2.69、1.42～2.76 MPa。在间排距0.5 m，预应力30、120 kN条件下，σ3为1.41～2.73、1.44～2.86 MPa。

图7 中岩墙最小主应力分布（单位：Pa）

中岩墙最大主应力分布见图8。可知：中岩墙无加固时最大主应力σ1为3.89～8.03 MPa。加固后在预应力为60 kN，间排距2.0、1.0、0.5 m条件下，σ1为3.92～8.09、4.37～8.35、4.78～8.62 MPa。在间排距为0.5 m，预应力30、120 kN条件下，σ1为4.77～8.57、4.82～8.74 MPa。

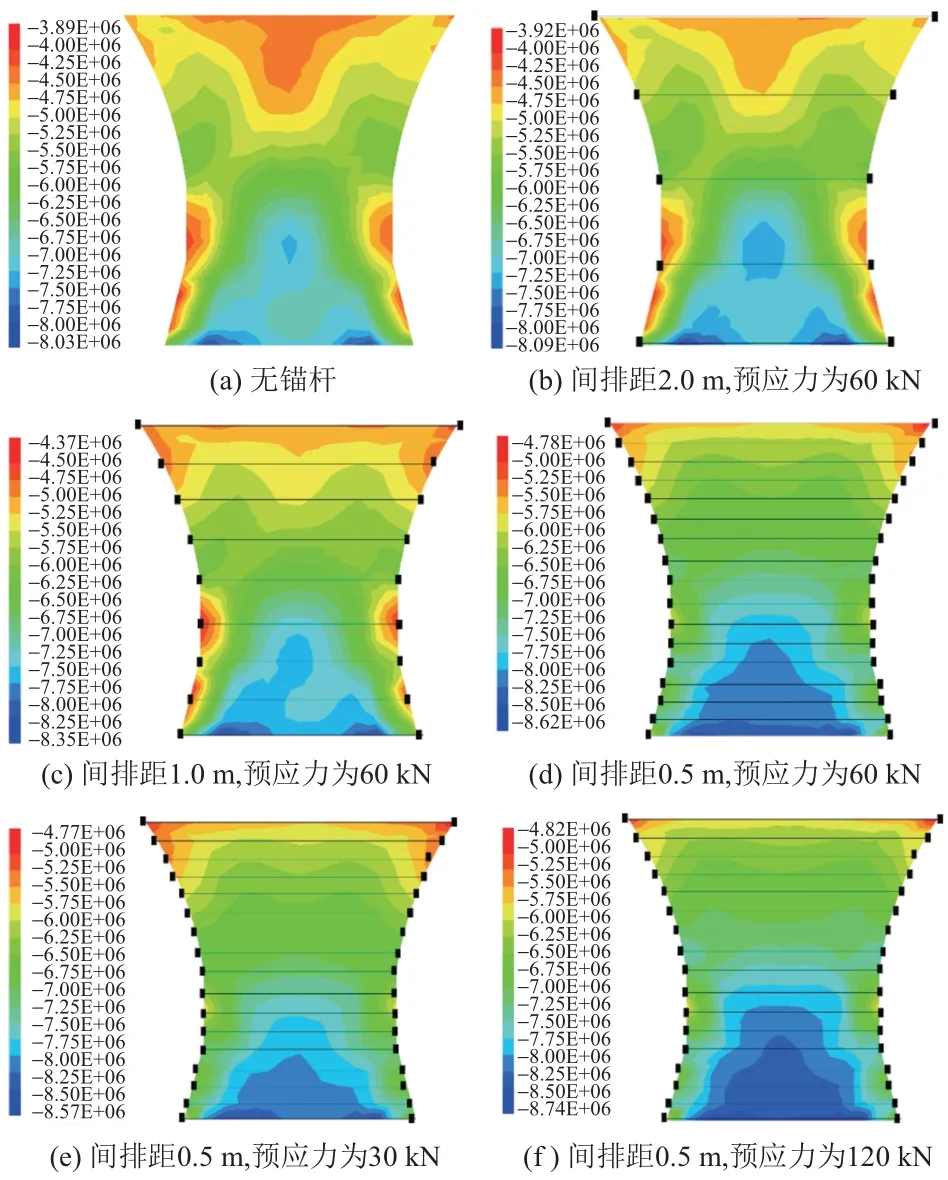
图8 中岩墙最大主应力分布（单位：Pa）

从中岩墙的应力分布图可以看出，无加固时，中岩墙顶部出现近似倒三角形的应力卸载区，底部出现三角形的应力集中区。施加对拉锚杆后，随着锚杆间排距减小和预应力增大，应力卸载区发展为带状甚至消失，应力集中区由三角形发展为梯形，最小主应力和最大主应力明显增大，应力变化与前述理论分析基本一致。

4 工程应用

为验证数值模拟计算的正确性，同时分析对拉锚杆加固后中岩墙位移特征，对上述数值模拟段进行现场监测对比分析。对拉锚杆间排距设计为1.0 m×1.0 m，预应力为60 kN，直径为25 mm，与模拟计算间排距1.0 m，预应力60 kN相对应。施工过程中，先开挖右侧洞室，后开挖左侧洞室。在中岩墙左右两侧上、中和下部分别布置6个位移监测点。隧道设计尺寸及位移监测点布置见图9。

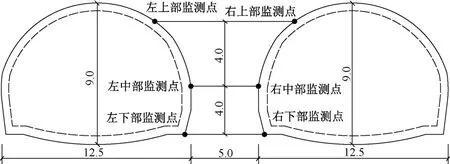
图9 隧道设计尺寸及位移监测点布置（单位：m）

中岩墙位移监测结果见图10。可知：开挖后前7 d最大变形速率为0.85 mm∕d，10 d后变形基本不变。水平位移和竖向位移最大值分别为6.1、7.2 mm，位于右侧中部和上部，最大值远低于QCR 9218—2015《铁路隧道监控量测技术规程》的容许值。通过左右两洞位移对比可以看出，对拉锚杆加固后，右洞的位移略大于左洞，这主要是由右洞首先开挖导致。通过位移现场监测与数值模拟的对比可以看出，现场监测值略小于数值模拟值，主要是由于施工中使用了注浆等预加固措施。

图10 中岩墙位移监测结果

对拉锚杆轴力变化曲线见图11。可知：顶部和底部锚杆轴力在前10 d存在预应力损失，此后轴力逐渐增大，20 d时达到稳定，顶部最大值约为102 kN，底部约为96 kN。中部对拉锚杆轴力持续增大，20 d时达到稳定，最大值约为112 kN。由于中岩墙中部水平位移大于顶部和底部，因此，中部锚杆轴力大于顶部和底部，中部锚杆未出现明显预应力损失现象，这与数值模拟结果基本一致。

图11 对拉锚杆轴力变化曲线

5 结论

1）通过建立中岩墙对拉锚杆加固力学模型，得到水平约束和力学参数的计算公式。影响加固效果的因素包括对拉锚杆设计参数、围岩力学参数等。

2）通过对中岩墙位移特征的分析可知，加固后竖向位移最大值由22.3 mm减小至9.6 mm，水平位移最大值由9.5 mm减小至2.3 mm。位移最大值和各监测点位移差明显减小，对拉锚杆间排距越小，预应力越大，加固效果越明显。

3）中岩墙承载时，在顶部出现应力卸载区，底部出现应力集中区，使用对拉锚杆加固后，中岩墙主应力增大。当锚杆间排距0.5 m，预应力120 kN时，顶部应力卸载区减小甚至消失，底部应力集中区扩展，承载能力增强。

4）通过现场实测可知，使用对拉锚杆加固的中岩墙最大变形速率为0.85 mm∕d，变形速率和变形值远低于规范容许值。中部锚杆轴力持续增大至112 kN左右，顶部和底部锚杆轴力先减小后增大至102 kN和96 kN左右，中部锚杆受力大于顶部和底部。