基于深度学习的配电网工程数据融合与智能分析方法研究
钟琦,杨 波,朱 莎,潘行健,陆非凡
(国网浙江德清县供电有限公司,浙江湖州 313200)
近年来,随着国内经济的快速发展,配网工程数据呈现出了爆炸式的增长,给数据的处理与分析带来了新的挑战[1-3]。与此同时,大数据处理技术、深度学习等人工智能技术的应用,也给电网配网工程数据的处理与分析带来了新的研究方向[4-5]。在配网工程数据领域,国内外专家学者对海量视频与数据库的自动化融合分析研究较少,仍处于研究起步阶段。如何充分利用现有数据资料,总结归纳采集数据的特征与规律,并将其应用于目标检测是目前研究的热点[6]。深度学习算法可用于特征提取,这些特征能够刻画出数据库的丰富内涵。其本质是通过神经网络,训练得到数据特征,并建立输出信号与输入信号的映射关系,为数据处理提供理论基础[7-8]。应用深度学习进行数据融合,可对多个来源的数据进行数据处理,具有准确性高、实时性强的特点[9]。有国外学者提出了关联分析的数据融合框架,以改善数据决策的鲁棒性,并将其应用于更广泛的交叉领域[10-12]。随着信息量的持续增加,配网工程数据来源更加多维,亟需应用更加精确的智能算法进行数据分析与处理。
该文以深度学习基础模型为理论基础,克服小规模数据特征提取较难的问题,并建立改进的FPFRCNN 检测模型。针对配网工程数据产生的异构大数据,分析配网数据的关联性与可靠性,将预处理结果作为数据源输入,进行电压和电流的采集,完成降噪处理和数据融合后,最终基于采集到的现场数据,实现数据挖掘和可视化分析。
1 深度学习模型
1.1 基本模型
深度学习是通过模拟大脑机理解决机器学习问题,因其强大的鲁棒性而被广泛关注[13-14]。在表达目标函数能力上,用深度结构的ANN 能较好地表示高维函数,但在优化参数过程中需要训练大量样本数据[15]。在模型训练方面,样本输入数据从一个模型迁移到另一个数据集,采用无监督方式获取更多的信息,其模型示意图如图1 所示。
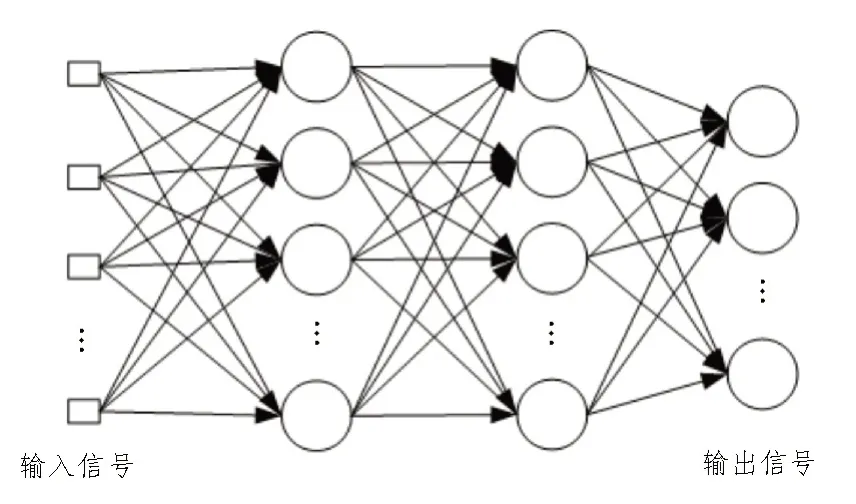
图1 深度学习神经网络模型
在可视层内,可以将输入信号看作特征节点,并认为所有节点均为独立的。因此,根据输入节点参数得到神经元参数,经处理后得到输出信号。
1.2 改进FP-FRCNN模型
为克服小规模数据特征提取较难的问题,建立改进的FP-FRCNN 检测模型,以提高检测精度。建立FP-FRCNN 模型首先需要压缩连接金字塔结构,该过程包括压缩激励密集与主干网络,同时修改Dense Net 网络结构。通过压缩操作对过渡层进行信息压缩,应用连接层构成激励操作,形成两个神经元单元之间的依赖关系[16]。最终,通过上述依赖关系对数据集进行重新校准。为了防止参数过程带来的影响,采用通道因子减少通道数量,直至恢复正常水平。构建金字塔网络结构的基本流程,如图2 所示。从图中可以看出,先对SE-Dense Net 的每个特征图进行卷积操作,并进行采样分析,自上而下重复上述操作,最终建立金字塔型网络结构。
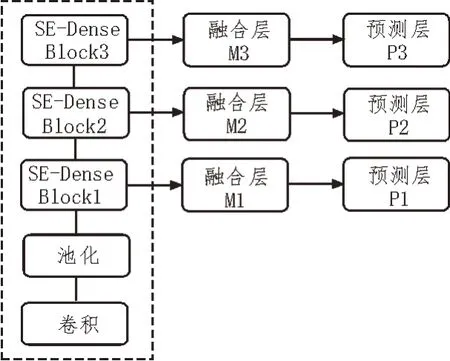
图2 金字塔网络结构构建过程
1.3 池化层调整
建立金字塔网络结构之后,需要将RPN 模块连接到预测层,然后将各个模块连接到RoIAlign 层,最后建立改进的FP-FRCNN模型,具体操作如图3所示。

图3 改进FP-FRCNN模型的整体结构
2 配网工程数据融合算法
2.1 数据预处理
配网工程数据呈现数据冗余、多维度等特征,如何高效利用该数据尤为重要。数据预处理是进行数据融合的前提,是决定数据智能决策与分析的关键步骤。针对配网工程产生的异构大数据,首先需要分析配网数据的关联性与可靠性,将预处理结果作为数据源输入。由于配网数据采集系统采用智能终端进行电压、电流的采集,并利用全智能分析技术进行降噪处理,因此还需要对原始数据样本集剔除异常数值,以提高配网工程的真实性。
为进行配网工程数据融合,设共有N个训练集样本,其子样本数据集分别为A1,A2,…,AN、B1,B2,…,BN和W1,W2,…,WN;关联训练子集为Y1,Y2,…,YN;则第i个样本可表示为:

将式(2)和式(3)分别扩展到式(1)中,可得到Yi为:
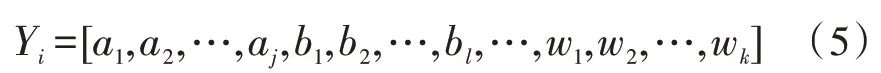
2.2 稀疏自编码器数据融合
配网工程数据不存在明显的分界,为标记工程数据的类别情况,采用基于聚类分析的稀疏自编码数据融合算法。该算法基于无监督学习,通过分类得到最终结果,可使输出数据尽量保存原有特征,其是一种强化的稀疏算法,且该方法的解码器变换可自动提取样本数据信息并进行深度学习。在损失函数方面,通过增加稀疏约束项,增加配网工程数据的特征提取能力,以提高数据提取的精确度。
稀疏自编码器数据融合算法流程如图4 所示,其主要步骤有三步:1)通过SAE 编码器建立稀疏自编码器,并对配网工程数据进行重构;2)通过神经网络设置初始参数,调用均方损失函数,采用Adam 优化器优化数据,防止过拟合现象;3)将SAE 输入,确定样本数据的中心点,通过计算确定数据核心与类别,经过多次迭代得到数据的分类结果。

图4 稀疏自编码器数据融合算法
2.3 边缘数据自适应增强
获取配网工程数据信息后,可以对数据信息做自适应增强处理,首先应保证局部数据信息的一致性,定义为:
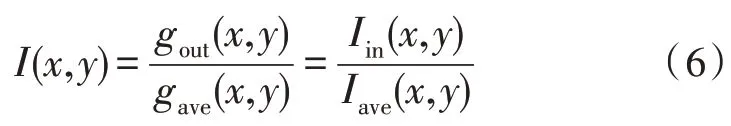
式(6)中,gout(x,y)、gave(x,y)分别表示经过二次泰勒级数展开卷积之后,配网工程数据在(x,y)位置的输出值与局部均值。
为保护边缘数据信息,将公式修改为:
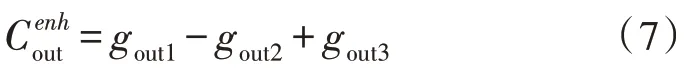
式(7)中,gout1、gout2、gout3分别是gout(x,y)的3个分量,若gout3>0,则可提高数据边缘信息,且的数值范围为[0,1]。
将处理后的数据信息还原为原始信息,还原公式为:
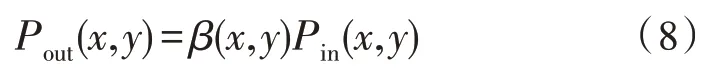
式(8)中,Pin为输入数据信息的分量值,Pout是指数据信息增强处理后得到的数据分量值,β(x,y)的定义为:
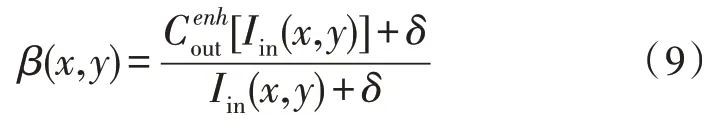
3 数据智能分析
3.1 原始数据可视化
配网工程数据可视化主要基于配网终端采集到的现场数据,进行储存、分析以及管理,实现数据挖掘、生产可视化界面。原始数据的可视化不仅给配网工程提供优质的计算服务,且为电力工程的推进提供有力支撑。根据可视化需求以及功能,生成用户账户,跳转到可视化界面,显示上传的配网工程原始数据,创建项目数据及模板,便于结构化管理。
通过Python 编程工具实现数据图像的呈现,直观显示配网工程数据的分布特征,将大部分数据显示在零点附近,使得数据排列呈现时间性,体现数据的电压、电流数值。
3.2 分析结果处理
配网工程数据分析一般有两种方法,即参数分析与波形分析。参数分析主要通过获取配网终端采集的数据特征进行数据分析,数据特征包括数据幅值、频率、持续时间等;波形分析是采用智能算法对波形信号进行处理分析频域特点,反映输入信号的规律,从而更好地应用波形信息。傅里叶谱分析方法是处理频域分析的常用方法,其分析结果可以用于全局信息处理。为避免数据丢失情况,并遏制数据混乱,运用Tfrsp 函数进行分析计算,得到二维频谱为:

3.3 评价指标
数据分析检测常用的精度检测指标平均精度(AP),通过计算预测值的准确率和召回率绘制P-R曲线,进而评价分析结果的效果。
分类精确率是针对给定数据集,分类数据量与总数据量的比值,若用M代表数据样本数,N代表数据集总量,则精确值可表示为:

一般来说,准确率与召回率为一对矛盾的度量方式,两者呈现负相关的关系。在选择评价指标时,需要考虑不同的场景与适用范围。为提高检测精度,需采用综合评价指标进行衡量。
4 算例分析
4.1 测试环境
以浙江省某区域配电网的实际工程数据进行算例分析,验证该文所提方法的有效性。数据分析实验均在带有GPU 的服务器上运行,CPU 为Intel Core i7 7800,显卡NVDIDA GTX1080,软件环境为Cuda 8.0/Python3.6/OpenCV。通过对比分析各种不同方法的配网工程数据处理结果,验证该文所提方法的识别精度与误差率。
4.2 结果分析
实验过程使用的配网工程样本数据库较大,采用该文所述深度学习模型,首先将样本数据进行分析与处理,利用差值算法分析数据集的损失。为验证数据缩放对检测精度的影响,在不同分辨率下分析检测精度,同时比较不同算法在不同分辨率情形下的效果。相应的计算结果,如表1 所示。从表中可以看出,几种方法均可以提升检测效果。且采用该文所述的深度学习方法时,AP 值达到了95.6%,具有良好的检测效果。
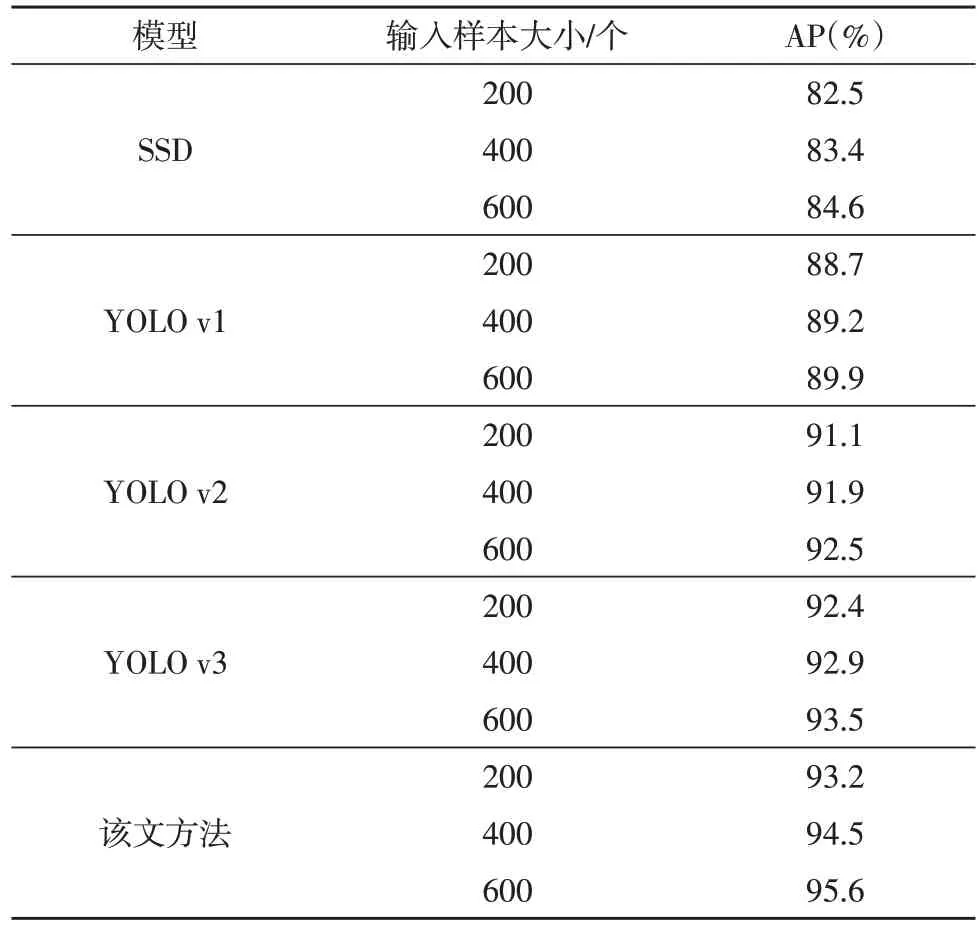
表1 几种方法的AP值
为进一步体现该文所述方法对配网工程数据融合的精度与误差,选取三种方法对该区域内的配网工程数据进行融合与分析,对比分析几种方法的有效性。三种方法的结果,如表2 所示。从表2 中可以看出,当采用深度学习对配网工程数据进行训练、融合、分析时,其结果的平均误差最小,处理精度更高。

表2 三种算法对比分析
5 结束语
针对配网工程数据分析与处理存在的问题,开展基于深度学习的配网工程数据融合与智能分析方法研究。通过建立改进的FP-FRCNN 检测模型、压缩连接金字塔结构,对配网异构数据进行融合分析;将预处理结果作为数据源输入,采用全智能分析技术进行降噪处理,基于聚类分析的稀疏自编码数据融合算法进行数据融合;利用配网终端采集到的现场数据,实现数据挖掘和可视化分析与处理;采用智能算法对波形信号处理分析频域特点,反映输入信号的规律与波形信息。最后,以某区域配网工程数据进行算例分析,验证了该文所述方法在不同分辨率下均具有良好的检测效果,且误差小、精度高,具有广阔的应用价值。下一步将研究改进的卷积神经网络与随机森林的识别算法,以更好地反映配网工程数据的数据特征,提高检测精度。

