氢/氧/惰性气体预混气可燃极限数值与试验研究

杜 宁 杨 岩 丁兆波 王希杰 王朝晖 张 帆 田 原

(1 北京航天动力研究所 北京 100076)

(2 航天推进技术研究院 西安 710100)

1 引言

液氢液氧火箭发动机氦密封系统的主要作用是防止或尽可能减少转动部件间推进剂的泄露,从而防止氢氧相混,以确保涡轮泵的安全工作。高效可靠的涡轮泵动密封已成为影响涡轮泵寿命和可靠性的重要因素之一[1]。氢能被国际社会誉为最具发展潜力的清洁能源,对“碳达峰”与“碳中和”发展目标的实现具有积极支撑作用。相比于其它燃料,氢的可燃边界较宽,在空气中可燃极限浓度为4%—75%,这就意味着氢泄漏更容易发生火灾甚至爆炸,严重制约了氢的工程化应用。因此,全面了解和掌握氢的可燃极限对氢能的生产、存储和运输具有重要意义。孙爱国等人[2]为提高微型低温制冷机的热力学效率,对不同配比的氢氦混合气进行爆炸试验,结果表明:氦对氢气具有一定阻燃作用,但只有当氦气占比达到50%以上时,阻燃效果才迅速增强;Coward 等人[3]通过试验研究得出,常温常压下氢的贫燃可燃极限体积分数为4%,当管径大于2 cm 时,对流热损失对可燃极限的影响较小,可以忽略对流传热影响;Kumar[4]研究了不同温度、压力和惰性气体对氢可燃极限的影响,试验结果表明,受浮力影响,火焰向上传播的贫燃可燃极限总高于火焰向下传播的试验结果,富燃可燃极限基本不受浮力和温度影响;Glukhov 等人[5]研究了低压下的氢/氧和氢/空气的可燃极限,试验结果表明氢/氧和氢/空气混合物的可燃极限压力分别为0.3 kPa 和0.076 kPa;Terpstra[6]通过试验与数值计算,研究了氢/空气/惰性气体混合物中的可燃极限,结果表明,绝热火焰温度法可以准确预测向上传播的氢/氧/惰性气体(氩气、二氧化碳和氮气)的贫燃可燃极限;Villegas[7]等人研究了有限空间内氢氧氦预混气的可燃极限,研究结果表明,随着氦气浓度的增加和间隙减小,氢可燃极限浓度以3%的体积分数线性增大;Zeldovich 等人[8]认为热损失是导致存在火焰极限的主要原因,并通过理论分析给出了火焰传传播速度与热损失的关系;Law 等人[9]从化学动力学的角度揭示可燃极限存在的原因,并提出判断依据,当链分支反应与链终止反应相等时,即:ωT—ωB,此时的火焰处于极限状况;随后,Law 和Egolfopoulo[10]进一步证明可燃极限的热损失理论和化学动力学理论实质上是统一的;Ma[11]提出了使用临界火焰温度法去评估碳氢燃料的可燃极限,但是这种方法在有氦惰性气体稀释或者混合物初始温度较高时,所预测的可燃极限有较大的误差;Jeon[12]等人提出非绝热火焰温度法以提高预测精度,然而,这种预测方法是基于试验结果对辐射热损失进行拟合得到,且使用条件要求氦气体积分数小于50%,存在一定局限性。

本研究针对液氢液氧火箭发动机氦密封系统实际工作环境,提出了一种新的基于热损失理论的氢氧氦混合气体可燃极限计算方法,并通过试验验证了该方法的准确性,确保了发动机高效可靠工作,同时本研究相关结论对于氢能的工程化应用也有一定参考作用。

2 数值计算

2.1 非绝热火焰渐进理论

根据大活化能渐进分析理论可知,火焰在可燃极限处的质量燃烧率和温度可以表示为:

式中:mf为非绝热火焰质量燃烧率,kg/(m2·s);Tf为非绝热火焰温度,K;mo为绝热火焰质量燃烧率,kg/(m2·s);To为绝热火焰温度,K;R为气体常数,J/(kg/K);Ea为活化能,kJ/mol;可以通过以下公式求解:

式中:mo和To通过利用anasys chemkin 商业软件平台求解一维绝热层流火焰控制方程得到。

2.2 辐射热损失影响

火焰向环境辐射热损失可以描述为以下两类:(1)从反应区向环境辐射热损失qrad1;(2)反应区向后反应区导热qrad2,后反应区受辐射热损失影响温度降低,如图1 所示。Mayer[13]和Jeon[12]研究表明,qrad1辐射热损失占比很小,可以忽略不计。因此,后反应区的一维非绝热能量守恒方程就可以表示为:

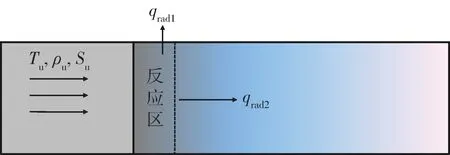
图1 火焰传播过程中两种辐射热损失机制Fig.1 Two radiative heat loss mechanisms in flame propagation

在后反应区,等式(4)的输运项远大于扩散项,因此,忽扩散项,辐射热损失qrad2可以表示为:

式中:su为非绝热层流火焰速度,m/s,ρu为反应物密度,kg/m3,cp为气体的定压比热,J/(kg·K),k为最高温度处的导热系数,W/(m·K),体积辐射热损失q(Tf)可以表示为:

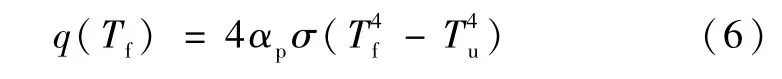
式中:Tu为环境温度,K;σ为玻尔兹曼常数,αp为气体总平均普朗特吸收系数,对于氢氧预混气,H2O 为主要的辐射组分。对于典型的光疏辐射模型,H2O 的平均普朗特吸收系数是一个温度的多项式函数[14],其拟合系数见表1,总的普朗特平均吸收系数可以表示为:

表1 水蒸气平均普朗特吸收系数拟合系数Table 1 Fitting coefficients of average Prandtl absorption coefficient of water vapor

式中:PH2O为燃烧产物中水蒸气的分压。

根据非绝热火焰能量守恒定律可知:

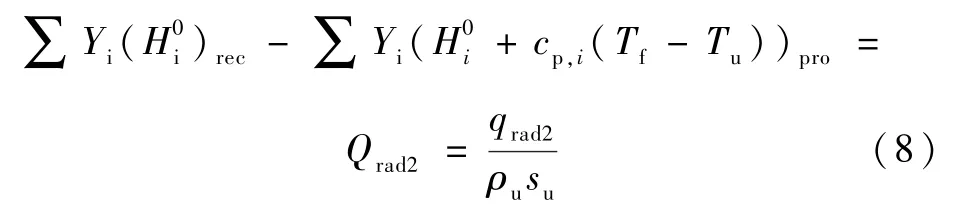
式中:为第i组分的生成焓,J/kg;Yi为质量分数;cp,i为定压比热容。下标rec 为反应物,pro 为生成物。

2.3 可燃极限计算

本研究可燃极限计算的过程如下,流程图如图2所示:

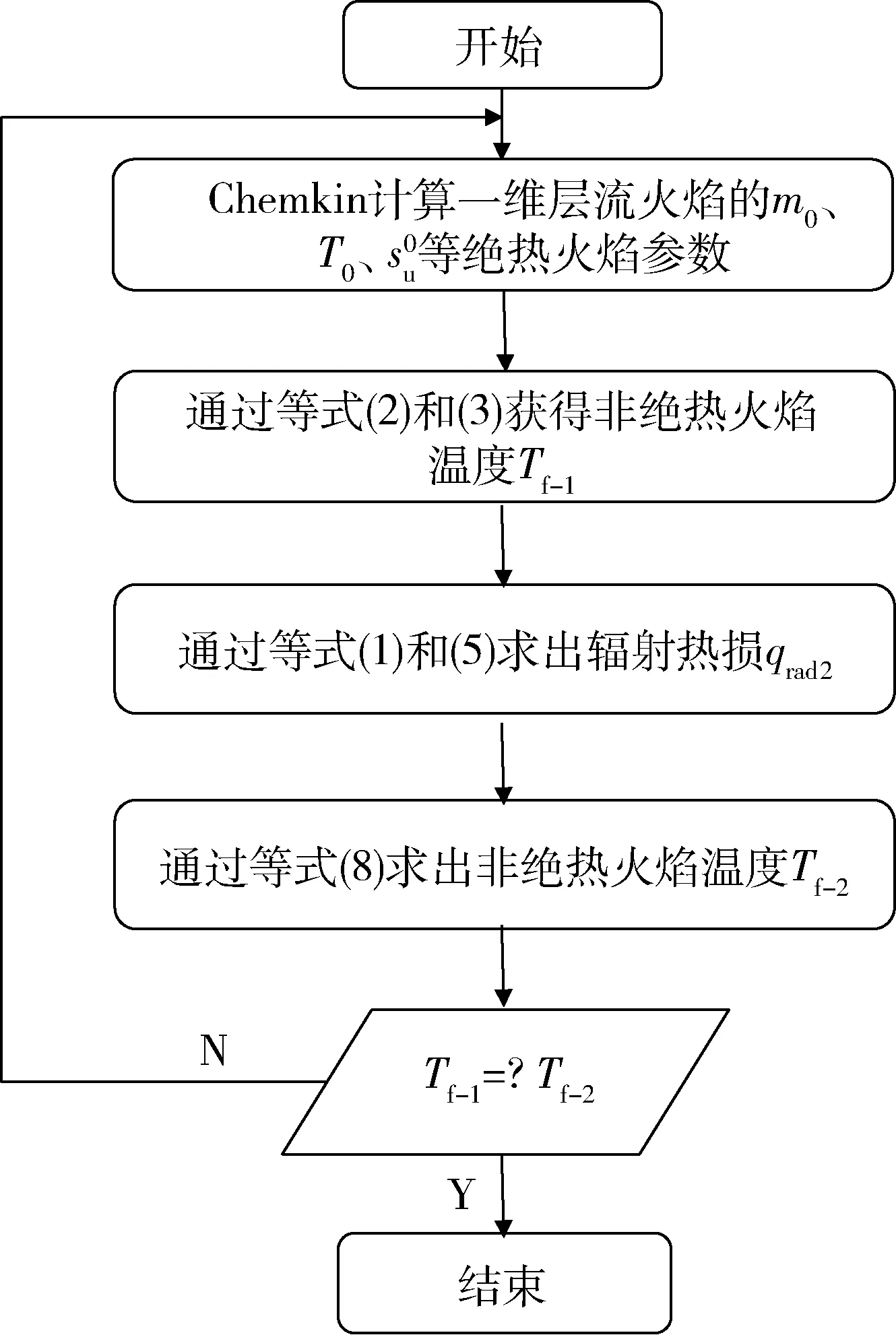
图2 可燃极限计算流程图Fig.2 Calculation flow chart of flammability limit

(1)首先利用Chemkin 软件计算贫燃或富燃区一维绝热自由传播火焰的速度、温度、密度和导热系数等参数;

(2)将式(1)计算的绝热火焰速度、温度和密度代入等式(5)求出对应的活化能,后将活化能和绝热火焰温度代入等式(2)求出非绝热火焰温度Tf-1;

(3)根据当量比可求出燃烧产物中水蒸气的分压以及质量分数,将水蒸气的分压代入等式(7)求出平均普朗特吸收系数,后将Tf-1代入等式(6)求出辐射热损失q(Tf-1)。

(4)假设所有计算工况的当量比混合物的质量燃烧率都适用于等式(1),因此可根据绝热火焰速度计算出非绝热火焰速度。进一步根据等式(5)计算出辐射热损失qrad2。

(5)把反应物和生成物的生成焓、各组分的质量分数以及辐射热损失qrad2代入等式(8)求出非绝热火焰温度Tf-2。

(6)通过对比Tf-1和Tf-2值,如果两者相差小于1 K,认为当量比下氢气的体积分数就是其可燃极限。

3 试验方案

本研究以文献[4]Kaumar 试验结果验证数值计算结果的准确性(下文简称Kaumar 试验结果),为了确认数值计算方法在氢氧火箭发动机中适用性,设计了如下试验系统(下文简称本研究试验结果):试验系统主要由氢阀、氧阀、氦阀、音速喷嘴、点火管、火花塞、真空舱等组成,系统原理图见图3。氧气和氦气混合之后进入点火管头部,与另一路气氢撞击后在点火管内充分预混,为了减小预混不均匀的影响,火花塞布置在点火管的出口,点火管长度为500 mm。内径为50 mm。点火管出口与真空舱连接。试验过程中通过改变氢/氧/氦音速喷嘴的喷前压力Pf/Po/PHe和喉部面积获取不同混合比的预混气体,通过改变真空舱内压力Pd研究压力对氢氧氦预混气可燃边界的影响,在真空舱内点火管出口处布置热电偶Te,通过判断热电偶测量的温度曲线以及试验过程中录像设备画面综合判断着火情况,试验参数见表2。

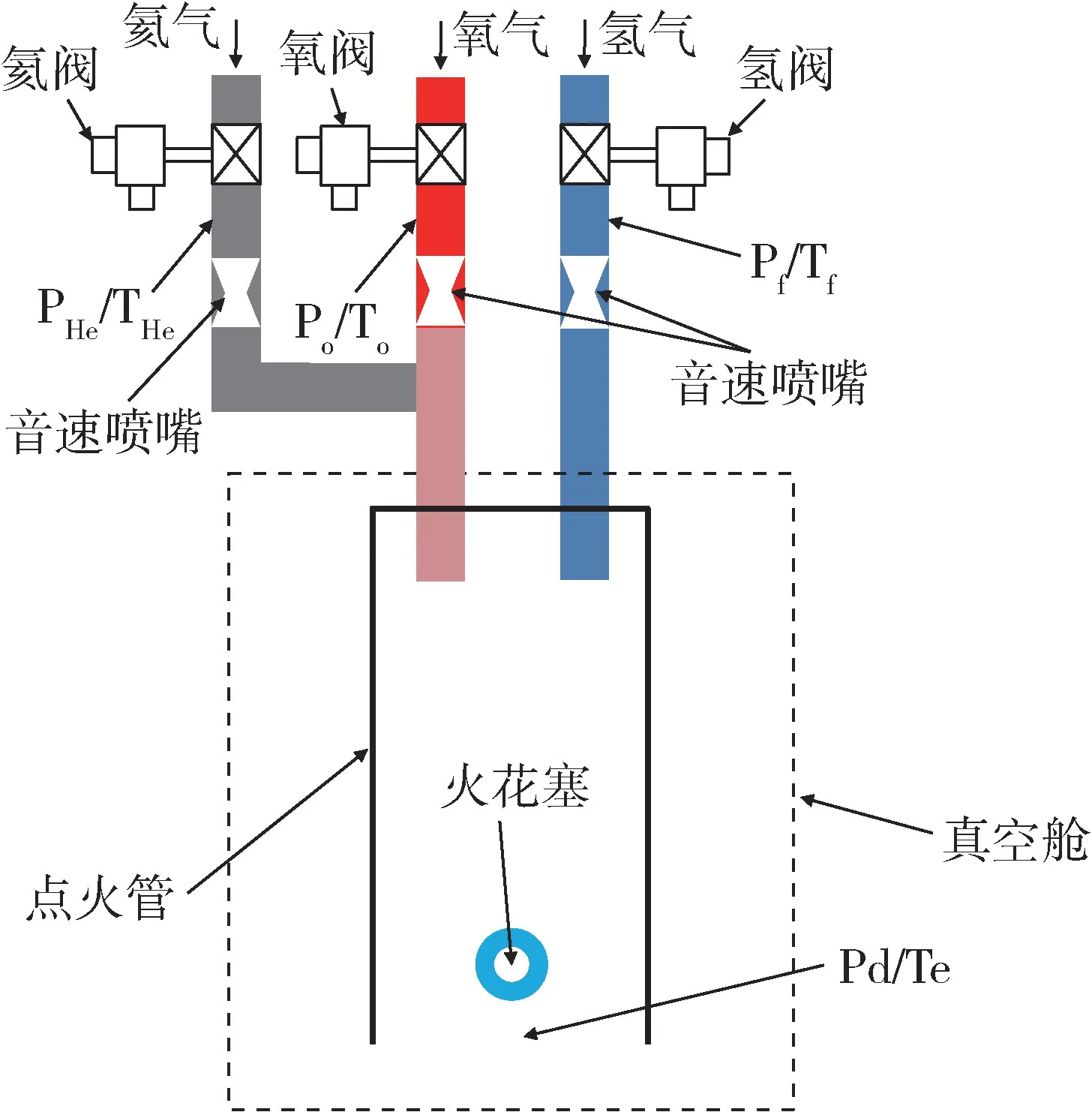
图3 试验系统原理图Fig.3 Schematic diagram of test system

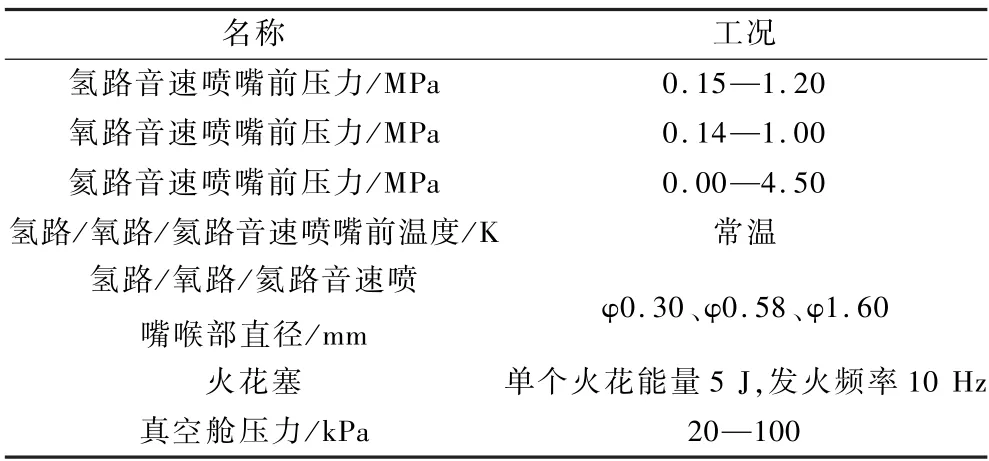
表2 氢氧氦可燃边界试验工况参数表Table 2 Experimental parameters for flammability limits of hydrogen,oxygen and helium premixed gas

4 结果与讨论

图4 给出了氢氧氮预混气可燃极限的Kaumar 试验结果与本研究计算结果对比。混合物初始压力为100 kPa,初始温度为295 K。对于富燃极限,氢氧氦预混气中氢气的可燃极限体积分数随着氮气体积分数增大线性减小,氧气体积分数保持在4%不变。对于贫燃极限来说,氢气的可燃极限的体积分数维持在10%左右,基本不受氮气体积分数的影响。这是因为氮气与氧气的物性相近,因此在氢氧预混气中混入部分氮气,其可燃极限不受氮气稀释影响。富燃极限的试验结构与数值结果误差小于2%,贫燃极限误差为15%左右,满足工程设计使用要求。贫燃可燃极限的计算结果误差较大,可能是由于贫燃可燃极限处火焰尺度较大,辐射计算模型未考虑辐射的重吸收效应导致计算的辐射热损失较大,从而过高评估贫燃可燃极限。

图4 氢氧氮预混气可燃极限试验与数值结果对比Fig.4 Comparison of experimental and numerical results of hydrogen-oxygen-nitrogen premixed gas flammability limit

图5 给出了氢氧氩预混气可燃极限的Kaumar 试验结果与计算结果对比。混合物初始压力为100 kPa,初始温度为295 K。与氢氧氮预混气可燃极限结果类似,对于富燃极限,氢氧氩预混气中氢气的可燃极限体积分数随着氮气体积分数增大线性减小,其氧气的体积分数从4%减小到3%。对于贫燃极限,可燃极限处氢气的体积分数随着氩气体积分数的增大而减小,与试验测量结果一致,这主要是由于氩气的物理性质与氧气相差较大,当氩气的体积分数增大时,混合物的平均比热和导热系数均减小,氢气的可燃极限减小。富燃极限的试验结果与数值结果误差小于2%,贫燃极限误差为15%左右,满足工程设计使用要求。

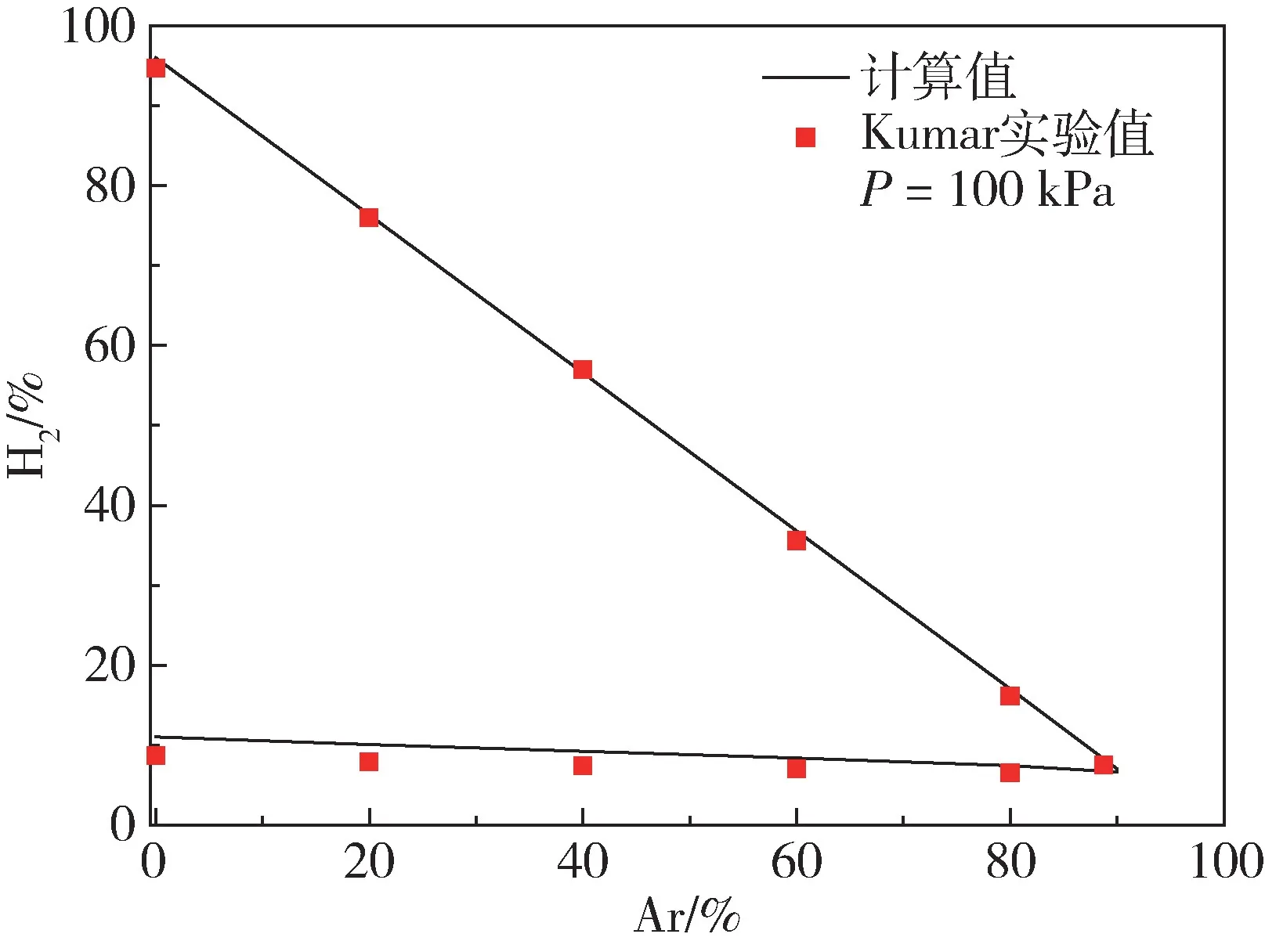
图5 氢氧氩预混气可燃极限试验与数值结果对比Fig.5 Comparison of experimental and numerical results of hydrogen-oxygen-argon premixed gas flammability limit

图6 给出了不同温度下氢氧氦预混气可燃极限的Kaumar 试验结果与本研究计算结果对比。混合物初始压力为100 kPa,初始温度分别为373 K 和473 K。试验与计算结果均表明,初始温度对富燃可燃极限影响较小,对贫燃极限影响较大,当初始混合物温度从373 K 增大到473 K,贫燃可燃极限降低了15%左右。由于混合物初始温度增高,火焰特征尺度减小,贫燃可燃极限误差减小至10%以内,富燃极限误差基本保持不变。该计算结果也表明本研究计算模型对不同的初始混合物温度工况同样适用。

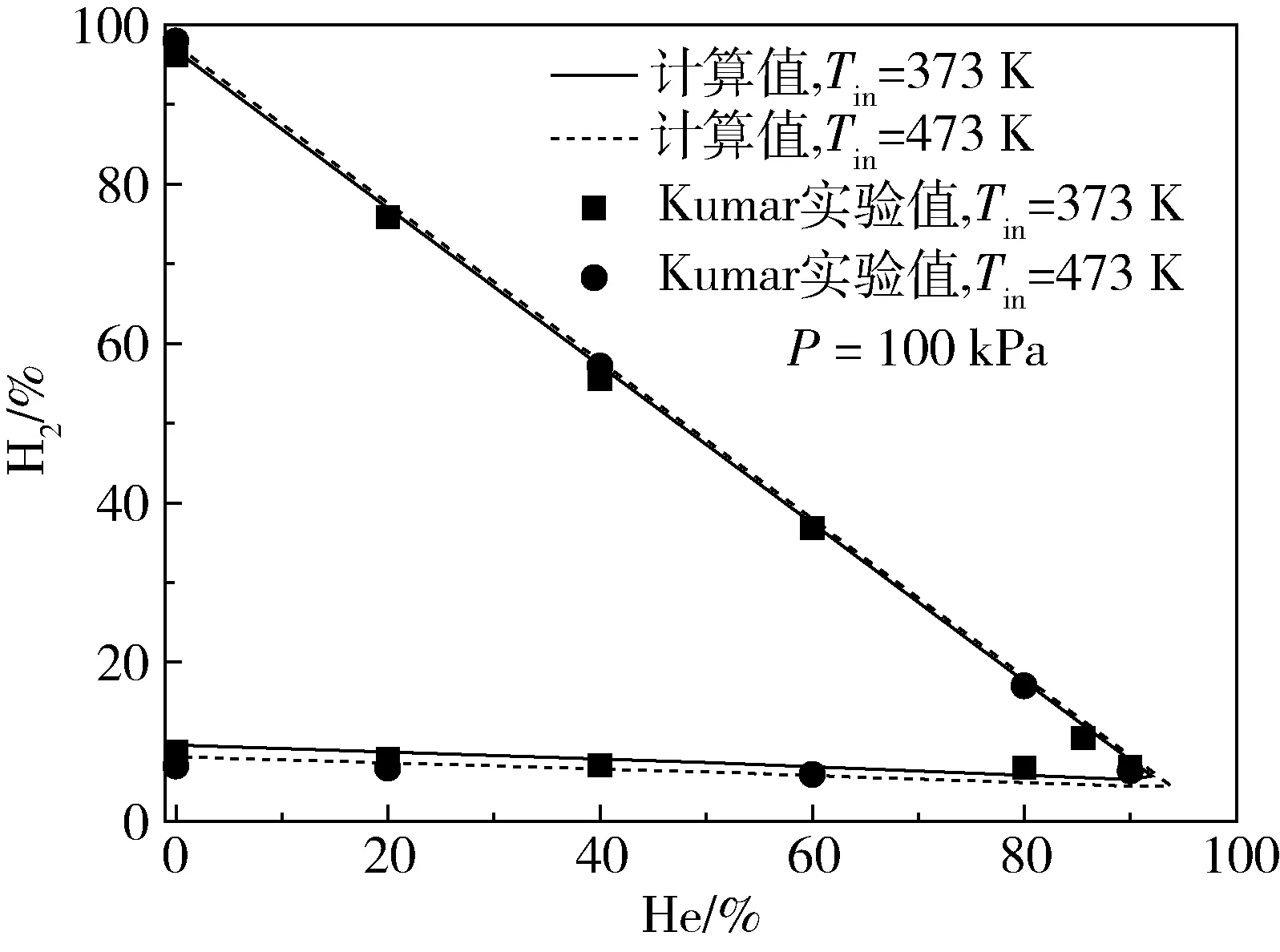
图6 不同温度下氢氧氦预混气可燃极限试验与数值结果对比Fig.6 Comparison of experimental and numerical results of hydrogen -oxygen-helium premixed gas flammability limit at different temperatures

图7 给出了不同压力下氢氧氦预混气可燃极限的本研究试验结果与计算结果对比。混合物初始温度为288 K,初始压力分别为20 kPa、50 kPa 和100 kPa。试验结果表明,可燃的混合物当量比处于计算可燃边界内,不可燃的混合物当量比处于计算可燃边界外,与理论计算边界基本一致。当混合物压力处于20—100 kPa,氢氧氦预混气的富燃可燃极限基本不受压力影响,而贫燃可燃极限氢气的体积分数随着压力减小而减小,这主要是由于压力降低时,平均普朗特吸收系数减小,辐射热损失减小所致。氦气与氩气具有相近的物性,因此,可燃极限随着氦气体积分数增加的变化趋势与氩气相同。试验结果与数值计算趋势保持一致,即本研究计算模型对不同初始压力工况同样适用。

图7 不同压力下氢氧氦预混气可燃极限试验与数值结果对比Fig.7 Comparison of experimental and numerical results of hydrogen-oxygen-helium premixed gas flammability limit at different pressures

5 结论

本研究通过试验与数值研究氢/氧/惰性气体混合气的可燃极限,获得以下主要结论:

(1)基于辐射热损失理论提出了一种新的氢/氧/惰性气体混合气可燃极限计算方法,并通过试验数据验证了该方法的准确性。

(2)数值计算结果表明,对于氢氧氮预混气体,氢气的可燃极限的体积分数基本不受氮气体积分数的影响。而对于氢氧氩/氦预混气体,随着氦气/氩气体积分数增加,氢气可燃极限体积分数减小。

(3)对于温度处于300—500 K,压力处于20—50 kPa,压力和温度的变化对氢氧氦富燃可燃极限影响较小,对贫燃可燃极限影响较大。