集成加速度计与GNSS的动态形变监测方法比较

杨宝山 柳 絮

(1. 中国石油化工股份有限公司胜利油田分公司海洋采油厂, 山东 东营 257000;2. 北京建筑大学 测绘与城市空间信息学院, 北京 102600)

0 引言

动态形变是评估结构动力响应特性的关键参数,监测动态形变对结构异常诊断与安全预警具有重要意义[1-2]。加速度计是一种常用的动态形变监测仪器,通过测量结构物发生位移时刻的加速度,经过两次积分获取动态形变,广泛应用于高楼、桥梁等大型结构物的动态形变监测中[3-4]。加速度计积分方法可分为时域积分和频域积分两种方法,其中时域积分误差易随时间累计,长时间使用精度差,且积分运算不易计算机实现[5-6]；频域积分通过傅里叶变换将信号从时域转换到频域,在频域内去除高低频噪声后,利用简单的除法便可完成积分运算,便于计算机实现,且无累计误差[7],但是,频域积分初始位置和速度难以确定,只能保证相对精度的可靠性。

另一种常用的监测方法是利用全球导航卫星系统(global navigation satellite system,GNSS)测量动态形变。GNSS技术具有全球性、全天候的高精度监测能力,是目前唯一能够提供被监测点三维绝对动态形变的手段。国内外学者利用GNSS技术已经开展了大量结构物形变监测研究,Roberts[8]利用全球定位系统(global positioning system,GPS)载波相位差分技术监测Forth Road Bridge 46 h内的交通负荷变化,结合傅里叶变换计算出振动频率,得出GPS既可以有效监测静态和准静态形变,同时可以监测动态形变；Górski[9]将GPS安装在工业烟囱上,测量在风的影响下烟囱的垂直剖面上的水平形变；现有研究表明,高频GNSS接收机能够较好地监测动态形变,但目前市场上的高频GNSS成本较高,而普遍使用的中低频GNSS在动态位移监测中仍受频率限制。此外,现有研究虽然在GNSS的多路径、观测噪声等误差的处理上取得了一定的进展和成果,但这些成果仅处于研究阶段,在实际应用中仍然难以满足毫米位移监测需求。

目前,已经有不少学者利用卡尔曼滤波对GNSS与加速度计数据做融合处理,以获取更高精度的动态位移。利用加速度计的高采样频率和GNSS获取的绝对形变,可以获取被监测点在高动态下的绝对动态形变。Li Xiaojing[10]利用实时动态载波相位差分技术(real time kinematic,RTK)和加速度计监测东京的铁塔,发现两者结果一致,增加了系统的冗余度；Meng[11]利用自适应卡尔曼滤波处理GPS数据,并与加速度计集成,实现了Wilford悬索桥的动态变形监测；韩厚增[12]基于经验模态分解改正GPS变形数据,通过加速度重构位移高频分量和GPS低频分量恢复桥梁真实结构响应,达到提取桥梁变形信息的目的。上述研究验证了GNSS与加速度计均能监测位移形变,两者之间具有一致性,但是并未对GNSS与加速度计的数据做融合处理。Chan[13]利用经验模态分解(empirical mode decomposition,EMD)去除GPS高频噪声和残差项,然后利用自适应卡尔曼滤波进行GNSS与加速度计数据融合,有效提高了形变监测的精度。上述研究表明,融合卡尔曼滤波可以有效提高形变监测精度,但依赖于稳健的卡尔曼滤波算法,在实测环境中,GNSS数据常常出现异常,加速度计数据也往往含有系统噪声,卡尔曼滤波的数学模型与噪声统计均具有不确定性,其复杂性远远超出了仅使用加速度计或GNSS监测动态形变。为了了解加速度计频域积分、GNSS以及GNSS、加速度计、卡尔曼滤波3种方法的动态形变监测效果及优缺点,本文利用模拟振动台开展了一系列不同振动频率的动态形变试验,通过横向与纵向比较,得出三种方法各自的长处与不足。并选取频域积分方法与GNSS/加速度计卡尔曼滤波方法作为重点研究对象,提出GNSS辅助确定初始位置的频域积分算法和GNSS/加速度计简易卡尔曼滤波算法,利用仿真与模拟振动台数据,验证两种算法的可靠性,并进一步比较分析所提方法各自的适用性与精度。

1 GNSS辅助确定初始位置的频域积分方法

由上文可知,频域积分在频域内通过简单的除法便可实现积分运算,易于计算机实现,并且通过设置截止频率有效去除了高低频噪声,无累计误差。但是,通过频域积分获取的振动位移初始位置具有随机性,只能保证相对精度。低频GNSS接收机虽然难以监测高频振动位移,但振动点位监测精度较高。本文通过GNSS确定加速度计频域积分序列的初始位置,确保加速度计频域积分监测位移的绝对精度。

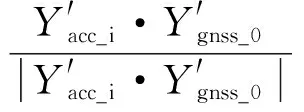
2 GNSS/加速度计卡尔曼滤波算法

GNSS与加速度计数据融合常采用卡尔曼滤波方法,一般将GNSS观测信息与加速度计观测信息同时纳入观测方程作为观测量,状态方程则采用一般动力学模型。由于监测点在振动过程做变加速度运动,状态方程至少为三维,观测方程为二维,本文尝试简化模型,通过将加速度计的观测信息作为状态方程的控制量,GNSS观测信息作为观测方程的观测量,构造简化的状态方程和观测方程为

式中,P表示位置；V表示速度；a表示加速度计观测量；Δt为加速度计的数据更新时间；w表示系统噪声；v表示观测噪声；k表示观测历元。

式(5)和式(6)可写成

式中,xk表示状态向量；φk,k-1表示状态转移矩阵；Γk-1表示控制矩阵；uk-1表示控制向量；Gk-1表示过程噪声驱动矩阵；wk-1表示过程噪声向量,且满足wk-1～N(0,Qk),Qk为过程噪声方差阵；zk表示观测向量；Hk表示观测矩阵；vk表示观测噪声向量,满足vk～N(0,Rk)。

3 振动台试验

2020年12月31日在北京建筑大学南门广场开展动态形变监测试验,使用的硬件设备包括模拟振动台、北京建筑大学自主研发的GNSS变形监测系统、荷兰Xsens公司生产的Mti300型号惯性测量单元(包括加速度计和陀螺仪,本试验仅使用加速度计)以及笔记本电脑。其中GNSS与加速度计性能参数见表1。

表1 GNSS与加速度计主要参数

对比GNSS、频域积分以及融合卡尔曼滤波三者之间在不同频率下的形变监测精度,从图1(为简化表达,FDIA表示改进频域积分方法,KF表示卡尔曼滤波方法)和表2可以看出,除0.5 Hz振动频率下,改进的频域积分方法精度最高,其次为GNSS形变监测,融合卡尔曼滤波结果最差,而仿真实验融合卡尔曼滤波较GNSS监测精度高,原因是实测数据GNSS与加速度计系统时间存在延迟。另外,实测加速度计数据虽然去除趋势项和高频噪声,但仍然存在残留的系统噪声,比仿真过程加的随机噪声更加复杂,导致融合卡尔曼滤波结果在实测中比仿真结果差。

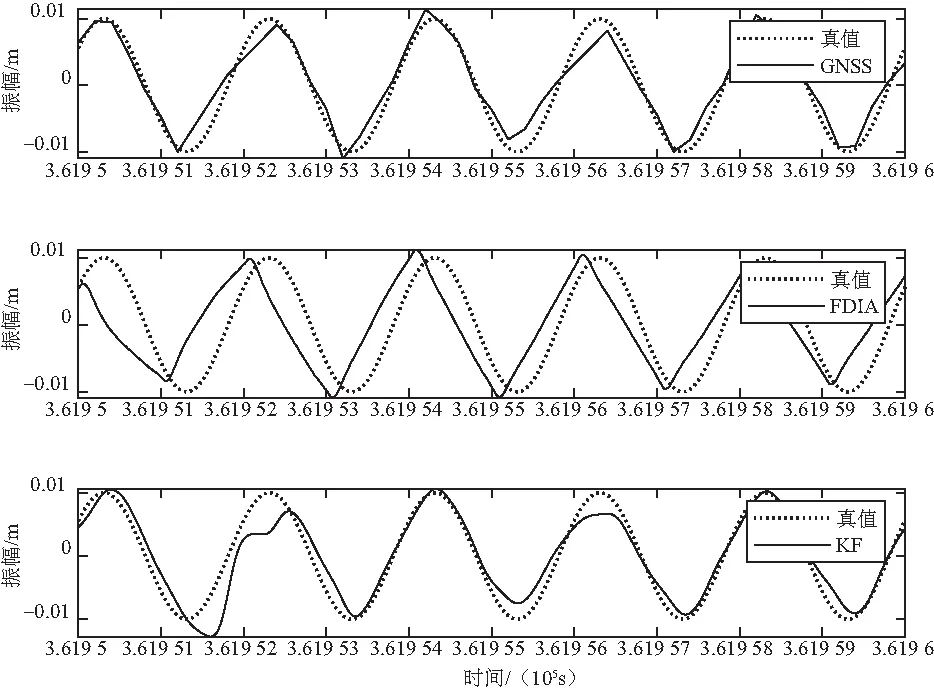
(a)GNSS/FDIA/KF结果比较(0.5 Hz)

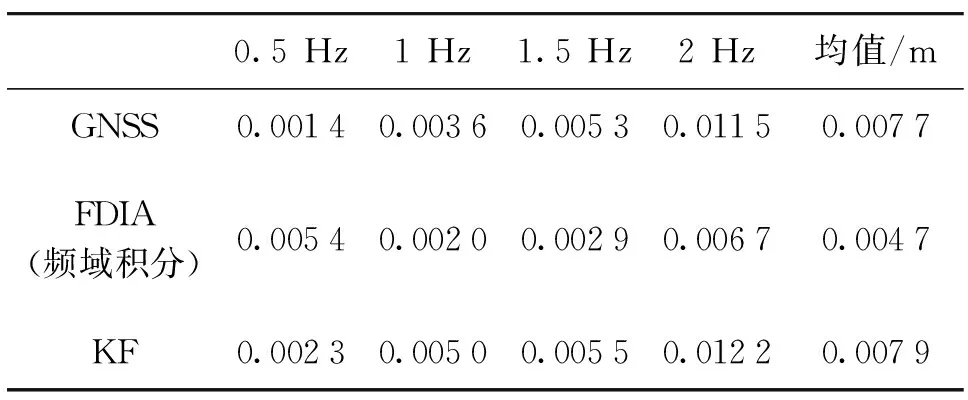
表2 GNSS/FDIA/KF在不同频率下的均方根误差

4 结束语

本文通过模拟振动台试验分析了加速度计频域积分、GNSS以及GNSS/加速度计融合卡尔曼滤波3种方法在监测动态形变过程中的优劣,并提出了GNSS辅助的频域积分方法以及简易GNSS/加速度计融合卡尔曼滤波算法,从实测数据中可以得到以下结论:

(1)根据奈奎斯采样理论,GNSS可监测1/2采样率及以下频率,但受实际环境影响,实测中往往难以监测较高的振动频率,当振动频率达到2 Hz时,采样频率为5 Hz的GNSS接收机已经难以准确监测形变位移。

(2)本文提出的改进的频域积分方法经仿真与实测验证,可以有效解决频域积分初值不确定的问题,提高了加速度计频域积分方法的绝对精度。

(3)本文提出了简易GNSS/加速度计融合卡尔曼滤波算法在仿真试验中可靠性较高,但是实测过程中受多种因素影响,监测精度差,卡尔曼滤波易发散。