稀疏训练指纹库融合MMPSO-ELM室内可见光定位
张慧颖,梁 誉,卢宇希,王 凯,于海越
(吉林化工学院 信息与控制工程学院,吉林 132022)
引 言
2019年,新型冠状病毒在全球范围内产生重大影响,保持一定社交距离对防控病毒传播效果显著,在室内和室外实现精确定位,在抗击疫情和今后应对其它病情上发挥关键作用。日本应庆大学研究小组结合发光二极管(light-emitting diode,LED)灯自身具备的功耗低、使用寿命长、无污染等优点率先提出基于LED可见光的通信概念[1]。随着人工智能技术研究和应用快速发展,结合机器学习算法的可见光室内定位技术成为研究热点。参考文献[2]中提出动量反向传播神经网络算法用于室内定位,最终定位平均误差达到10.18cm~11.4cm,其在1.8m×1.8m×2.1m特定空间内实现,具有一定局限性,并未考虑光信号多径传播及外界噪声对定位影响。参考文献[3]中提出利用一种有监督人工神经网络进行精确的3维可见光定位(visible light positioning,VLP),同时使用接收机分集技术克服可见光多径传播对定位的影响,该系统对视距(line of sight,LOS)和非视距(non line of sight,NLOS)链路平均均方根误差(root mean square,RMS)分别为0.0198m和0.021m,该研究克服多径传播对定位的影响,但仍使用传统反向传播神经网络算法,定位精度欠佳。参考文献[4]中提出基于误差学习和匹配的到达时间(time of amival,TOA)的人工神经网络定位算法训练测量距离值,输出距离误差而不是光电二极管(photo diode,PD)接收器位置,此方法较人工神经网络定位精度提高0.5m,但在定位阶段单一利用聚类导致结果存在偏差。HUANG等人提出了极限学习机(extreme learning machine,ELM)的新概念[5]。参考文献[6]中提出应用多层ELM来提高边界区域的定位精度,但内部区域定位未得到提升。参考文献[7]和参考文献[8]中均考虑接收器倾斜与多径反射对定位影响,参考文献[8]中通过改变发射机朝向平面中心高度,实现接收功率水平最大化,定位精度明显提高,但此方法增加布置设备成本,使得适用性不广。参考文献[9]中针对目前可见光定位接收器高度大多固定假设,提出通过直接可测量位移改变接收器高度的方法,降低3维空间定位高度误差,但此方法针对2维平面的定位误差没有做到改善。参考文献[10]中提出改进k均值聚类算法对房间接收点分为两个聚类,降低房间边缘定位误差。参考文献[11]中对定位误差与LED有效发射角以及接收器视场角之间变化关系做了研究,选定最佳接收视场角为60°,此方法同样有设备成本较高、适用性不强的缺点。参考文献[12]和参考文献[13]中分别提出基于指纹库的三角定位和后向传播(back propagation,BP)神经网络两步实现定位,但需大量指纹参考点数据,增加了前期工作量。
针对现有可见光室内定位方法存在的不足,本文作者提出建立考虑可见光视距与非视距传播的指纹库方法来增加房间边界区域参考点的接收光功率,保证房间边界与内部定位性能基本一致;利用稀疏训练数据达到较好训练结果;采用多目标动量粒子群优化融合极限学习机定位方法实现室内可见光高精度定位。针对不同房间大小及不同数量测试集下的仿真结果表明,基于稀疏训练指纹库融合多目标动量粒子群优化和极限学习机(multi-objective momentum particle swarm optimization-extreme learning machine,MMPSO-ELM)定位方法具有精度更高、定位速度更快等优点,是一种泛化性更强的室内VLP方案。
1 信道模型与定位原理
光信号在信道中传播符合朗伯模型[14],包含LOS传播和NLOS传播,其中PD接收端在LOS传播条件下光直流增益HLOS(0)为[15]:
HLOS(0)=
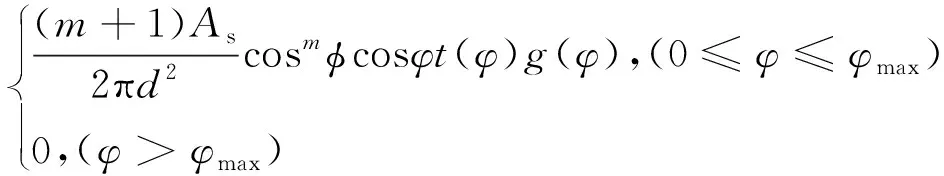
(1)
式中,m为朗伯系数,d为发射端与接收端距离,As为接收端面积,φ为发射角,φmax为LED最大发射角,φ为入射角,t(φ)为光学滤波增益,g(φ)为光学聚光器增益[16]。
PD接收端接收到一次墙面反射的直流增益Href(0)为:
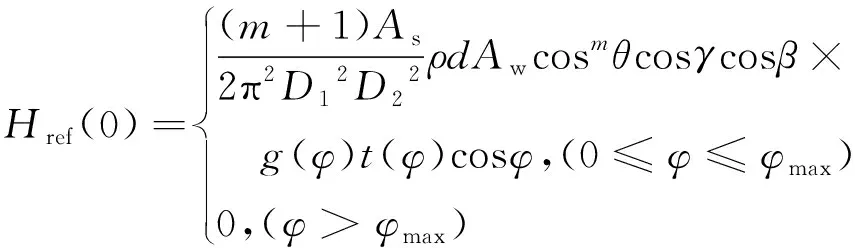
(2)
式中,Aw为墙面反射单位面积,D1为发射端到墙面反射点距离,D2为墙面反射点到PD接收端距离,θ为反射点发射角,γ为墙面反射系数,β为反射点处接收角。
在室内可见光传播过程中热噪声、散粒噪声及人为因素会对定位效果产生影响[17-18],用σn表示,则PD探测到的信号总功率Ps为:
Ps=Pt[HLOS(0)+Href(0)]+σn
(3)
式中,Pt为LED灯源发射总功率。
2 稀疏训练指纹库融合MMPSO-ELM室内定位方案设计
2.1 指纹库定位模型建立
定位过程中与移动PD接收端位置相关指纹参考点较少,因此,为降低房间内采样点密度,减少采集数据量,采用均匀分布采样点方法收集来自不同LED光功率值。建立指纹库工作流程为:(1)均匀选择100个坐标点作为室内指纹参考点;(2)分别计算从4个LED接收的光功率;(3)将墙壁划分为面积为1dm2的反射面,反射面每反射一次就计算指纹点接收到的LED功率;(4)向采集的数据中加入高斯白噪声,模拟环境中的热噪声和散粒噪声;(5)对数据进行预处理,筛选异常值,完成指纹数据库的构建。
针对3m×3m×3m与6m×5m×3m房间内建立基于LED室内定位指纹库模型分别如图1、图2所示。LED0、LED1、LED2、LED3为均匀安装在天花板上4个各自独立的信号发射机,指纹参考点均匀分布在水平高度为0m的地面上。
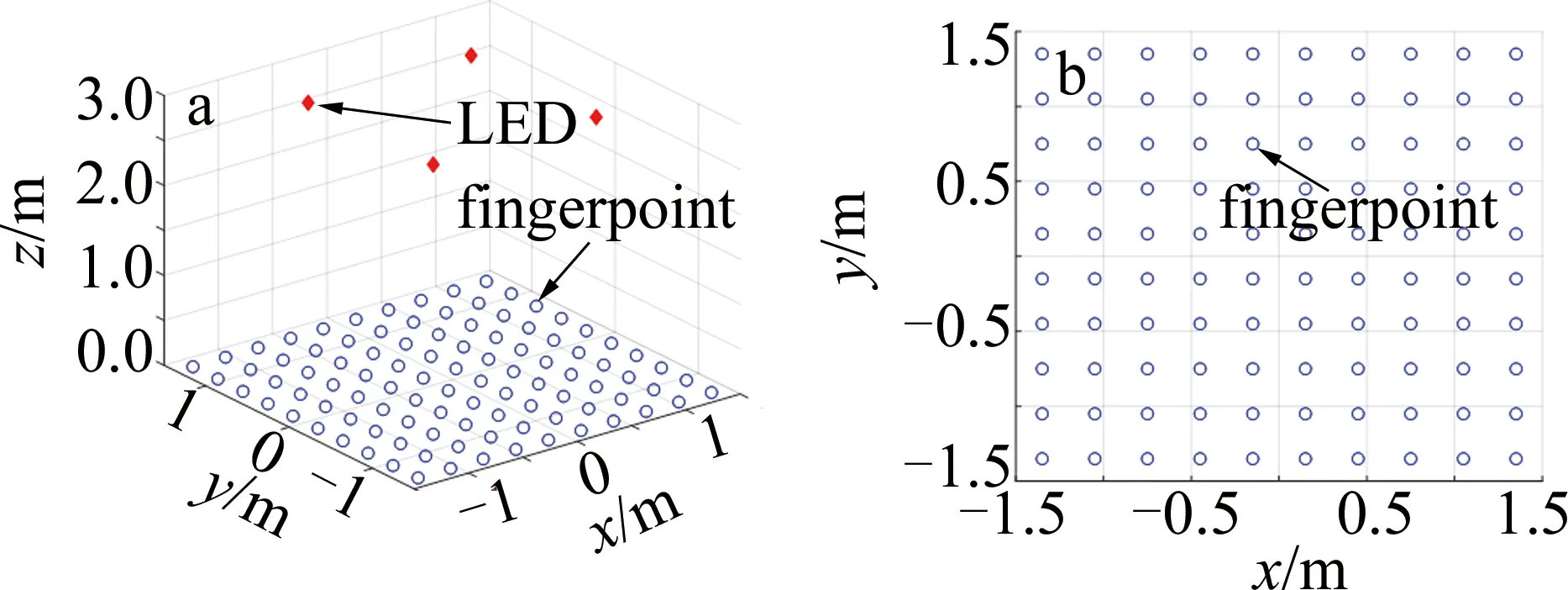
Fig.1 3m×3m×3m indoor positioning fingerprint databasea—3-D space model b—2-D plane model

Fig.2 6m×5m×3m indoor positioning fingerprint databasea—3-D space model b—2-D plane model
2.2 MMPSO-ELM室内可见光定位算法设计
考虑稀疏训练数据集易导致神经网络出现过拟合现象[19-20],因此选用单隐层前向传播ELM作为研究对象,本文中将定位过程划分为离线训练和在线定位两个阶段:离线训练阶段随机从接收光功率指纹库中选取仅20组数据作为网络训练样本,假设输入层Q组样本(xi,ti),xi为输入层输入端训练数据,ti为输入层输出端训练数据,选定隐藏层神经元对应激活函数为
h(·),则ELM隐藏层矩阵H为:
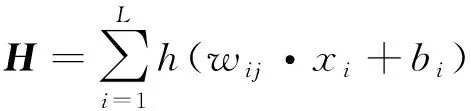
(4)
式中,wij表示输入层第i个神经元与隐藏层第j个神经元之间连接权值,bi表示隐藏层第i个神经元的阈值,L表示隐藏层神经元个数。输出层矩阵T表示为:
(5)
式中,βi为隐藏层与输出层连接权值,Y为输出层神经元数量。
传统粒子群优化极限学习机神经网络[21-22]是利用ELM初始权值、阈值矩阵随机生成,使ELM运算速度得到提升,但增加运算结果不确定性。本文中将粒子群算法适应度函数设置为神经网络实际输出与期望输出之间最短欧氏距离:

(6)

(7)
式中,C矩阵由ELM初始权值矩阵与阈值矩阵构成,而权值矩阵可用W表示:

(8)
阈值矩阵可用B表示:
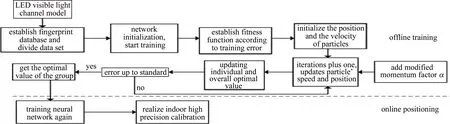
Fig.3 Flow chart of indoor VLP based on sparse training fingerprint database and MMPSO-ELM model
B=[b1b2…bL]
(9)
为提高算法收敛速度,避免陷入局部最优值以及过度振荡,本文中在传统粒子更新规则基础之上,加入符合高斯分布随机动量因子α,用α指导PSO对ELM初始权值矩阵与阈值矩阵寻优更新,从粒子群中寻得全局最优粒子速度与粒子位置作为ELM的最优连接权重矩阵和阈值矩阵。
根据(4)式~(9)式,分别对粒子速度、位置、适应度函数值进行更新,在加入动量因子条件下以较少迭代次数达到预设最小适应度值fmin,将得到的粒子最优位置作为ELM神经网络权值与阈值矩阵进行训练,输入N组训练数据,输入层5个神经元分别表示指纹点分别接收得到来自4个LED直射光功率、来自墙面一次反射总功率以及符合正态分布加性高斯白噪声,隐藏层神经元个数设定为N-2个,输出层神经元为待定位点横、纵坐标值。
在线定位阶段,随机从指纹库100组数据中多次选取80组数据作为测试集输入到训练完成的动量融合ELM模型中,得到定位结果,用网络输出与期望输出计算定位误差。基于稀疏训练指纹库融合MMPSO-ELM室内高精度可见光定位流程如图3所示。
3 仿真测试与结果分析
仿真实验地点选在吉林化工学院现代通信技术实验室内某一区域,采样区域大小分别为3m×3m×3m和6m×5m×3m,取地面中心为坐标原点,4组LED灯排均匀安装在距离地面3m高度的屋顶,坐标分别为(0.75m,0.75m,3m),(-0.75m,0.75m,3m),(0.75m,-0.75m,3m),(-0.75m,-0.75m,3m);(-1.5m,1.25m,3m),(1.5m,1.25m,3m),(-1.5m,-1.25m,3m),(1.5m,-1.25m,3m)。在考虑LED信道直射与墙面一次反射条件下,得到3m×3m×3m室内指纹参考点接收光功率数据,接收功率分布如图4所示。
仿真参数设置如下:单个LED发射功率为0.73W,每组灯群包括5×5个LED灯,LED的发射半角为60°,光电二极管的面积为2cm2,光滤波器增益及光集中器增益均设置为1,墙面反射单位区域的面积为9cm2,反射因子为0.6。粒子群算法在对ELM的初始权值与阈值矩阵进行寻优时,设定加速度因子c1和c2分别为1.19和0.65,粒子的位置与速度均在[0,1]范围内,最大权值wmax设为0.9,最小权值wmin设为0.2,适应度函数最小值fmin设置为0.00001mm,最高迭代次数为250次。采用同样训练集、测试集数据分别对BP、ELM以及PSO-ELM进行神经网络训练与测试,定位效果如图5所示。
如图5a所示, BP神经网络用于室内预测定位偏差较大,测试集平均误差为0.163m;如图5b所示,ELM定位算法测试集平均误差为0.118m,定位性能优于BP神经网络;如图5c所示,基于PSO-ELM室内定位算法平均定位误差为0.035m,具有较好定位效果;如图5d所示,本文中提出的MMPSO-ELM定位方案平均误差低至0.0065m,定位精度明显优于其它3种神经网络算法,为进一步验证MMPSO-ELM室内定位方案泛化性能,分别在待定位点个数为20、40、60、80情况下进行定位,得出各算法在房间内总体平均误差随带定位点数量变化趋势如图6所示。

Fig.4 Simulation results of the received power of fingerprint reference point
如图6所示,基于BP神经网络定位算法在待定位点较少时定位效果较好,但待测点数量较多时定位误差会随之大幅度增加,4种算法在测试样本数不同条件下的仿真结果如表2所示。
由表2可知,另外3种方法定位误差受待测点数量变化影响较小,且本文中提出的基于MMPAO-ELM定位方案定位误差均为最小。分别对BP、ELM、PSO-ELM及MMPSO-ELM在测试数据集上定位误差分布进行仿真,3维曲面结果如图7所示。
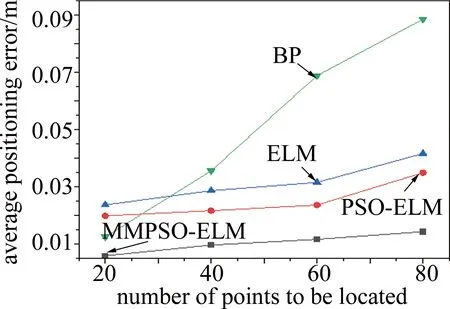
Fig.6 Variation trend of the average positioning error of four neural network positioning algorithms with the number of points to be located
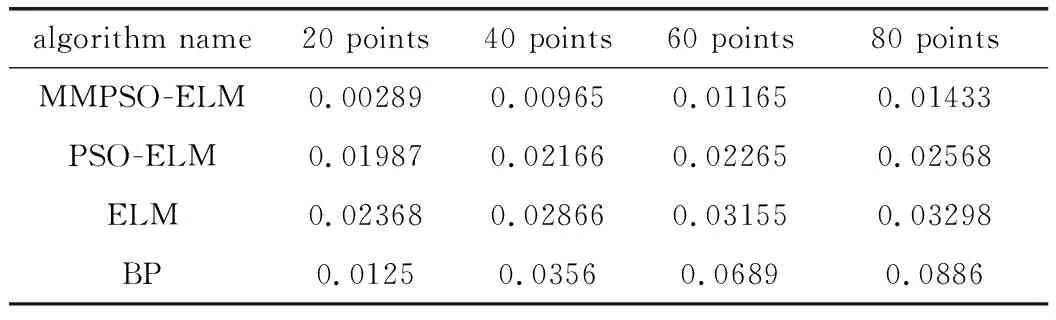
Table 2 Average positioning error under different number of points to be measured/m
如图7所示,BP、ELM两种神经网络定位算法在房间4个角落定位误差较大; PSO-ELM定位算法对房间边界区域的预测定位效果相较BP、ELM有所改善;本文中提出的MMPSO-ELM方案整体定位效果显著提高,相较于其它方法定位精度大幅度提升。
对4种神经网络定位方法的性能指标进行分析得到:基于BP神经网络定位方法在对80个测试点进行定位,最大定位误差为0.4740m,最小定位误差为0.0037m,平均定位误差均为0.0886m;基于ELM神经网络定位方法在对80个测试点进行定位,最大定位误差为0.1702m,最小误差为0.0012m,平均定位误差均为0.0329m;现有基于PSO-ELM定位方法在测试集上最大误差为0.03886m,最小定位误差为0.0011m,平均定位误差为0.02568m;本文中提出的MMPSO-ELM定位方案在测试集上最大误差为0.0225m,最小误差为0.00093m,平均定位误差为0.00143m。仿真结果表明:MMPSO-ELM室内定位方案定位精度明显优于现存几种机器学习定位方法。
选定在测试点为40组相同条件下,采用上述4种定位方法实现定位预测,分别得到定位误差在0m~0.01m,0.01m~0.05m,0.05m~0.1m,大于0.1m 4个区间内所占比例,误差占比直方图如图8所示。
如图8所示,定位误差区间为0m~0.01m时,MMPSO-ELM定位方法所占比例为64%、PSO-ELM占比为51%、ELM算法占比为29%、BP所占比例仅为16%,本文中提出定位方案精度远高于另外3种算法;定位误差区间为0.01m~0.05m时MMPSO-ELM占比为16%、PSO-ELM占比为28%、ELM占比21%、BP占比为24%;定位误差区间为0.05m~0.1m时,MMPSO-ELM所占比例为16%、PSO-ELM占比为9%、ELM占比为39%、BP所占比例达到31%;当定位误差大于0.1m时,MMPSO-ELM占比低至2%、PSO-ELM占比为12%、ELM占比11%,BP占比达到29%。上述仿真结果表明:在稀疏训练集条件下, MMPSO-ELM定位误差主要集中在0m~0.01m区间内,因此说明MMP-SO-ELM定位方法是一种具有高精度、较强泛化性的室内可见光定位技术。在20组训练集条件下,4种神经网络算法训练时间与仿真测试平均误差结果如图9所示。

Fig.7 Figures of positioning error based on various algorithms

Fig.8 Histogram of the proportion of algorithm location error

Fig.9 Neural network training time and simulation test error

Fig.10 Positioning simulation results
由图9可得,在训练集数量均为20组时,MMPSO-ELM训练时间为3.803s、PSO-ELM训练时间为8.7457s、ELM训练时间为3.21s、BP训练时间为12.0073s;ELM神经网络训练时间最短,但定位误差最大,MMPSO-ELM在训练时间虽比ELM训练时间略长,但具有定位精度高的优点。保持以上定位参数不变情况下,选取室内空间面积为6m×5m×3m,定位仿真结果如图10所示。
由图10可得,对50个待定位点进行预测定位得到最大定位误差为0.0216m,最小定位误差为0.00034m,平均定位误差为0.003m,MMPSO-ELM网络训练时间为4.303s,定位时间为0.02513s,与3m×3m×3m室内定位结果相比,本文中提出的定位算法受空间增大影响较小,因此,基于稀疏指纹库融合MMPSO-ELM的定位方案具有定位速度快、精度高、泛化性强等优点。
4 结 论
本文中利用均匀稀疏分布采样方法建立室内可见接收光功率指纹库,采用稀疏训练MMPSO-ELM神经网络实现可见光室内定位方案设计。通过加入动量因子加快ELM最优权值矩阵与阈值矩阵的更新,解决了ELM随机生成初始参数导致定位结果稳定性较差问题,加快PSO收敛速度,可避免过拟合现象发生,实现了高精度室内定位。在定位空间为3m×3m×3m区域内的仿真结果表明:本文中设计的室内可见光定位方案在任意数量测试样本的定位误差稳定在0.01m内,定位精度相较BP、ELM、PSO-ELM 3种神经网络算法分别提高83.82%,46.54%,34.19%,在最大定位区域内利用最少训练数据实现高精度定位,网络训练时间仅需3.803s,定位时间低至0.06s;当增大定位空间时,定位精度、定位时间均变化不大。因此,稀疏训练指纹库融合MMPSO-ELM室内定位方案具有训练速度快、定位误差小、泛化性强等优点,所研究内容为室内可见光定位实现提供了理论支撑。

