克里金模型用于预测聚能射流速度的方法研究

雷婧宇，王利侠，寇鹏飞，薛 标

(西安近代化学研究所，陕西 西安 710065)

引 言

聚能装药是目前及未来用以打击装甲目标最有效的战斗部形式之一[1]，它依靠炸药对药型罩进行爆炸加载，从而形成定向、高速射流，以此穿透并击毁目标。要使聚能装药对目标具有较高的打击能力，所形成的射流必须具备速度高、连续性好等特点。由于聚能装药爆炸形成射流的过程非常复杂，而获得射流速度需要求解非线性函数，因而往往难以获得其精确的解析值。另外，作为有效近似手段的数值模拟法也会受到材料本构模型及所用动态参数等因素的制约[2]。

聚能射流的速度一般可通过定常理想不可压缩流体力学理论模型来估计[3]，但预测结果往往过高，且不能反映射流速度梯度及射流的伸长，而后发展的PER准定常理论[4]，可以进一步预测射流的速度梯度和长度。

一些学者建立了理论模型或经验模型，以快速预测聚能装药的部分响应量[5-8]。黄正祥等[9]应用灰色预测模型，对聚能射流侵彻陶瓷装甲的侵彻深度进行了预估。近年来，神经网络逐渐被应用到聚能装药的射流速度预测中[10-11]，其预测结果较为准确，且计算速度相比数值模拟更快，能够实现对聚能射流速度的快速计算模拟。相比理论模型与灰色预测模型，神经网络所建立的模型灵活度以及精准度更高，且模型训练的过程不需要复杂的理论推导过程，具有较好的发展前景。然而，神经网络所建立的模型往往比较庞大，且其神经元的个数以及网络层数往往难以确定。

克里金代理模型由南非采矿工程师Krige提出[12]，后来发展为统计学的一类插值方法。克里金模型通过训练样本与其函数值之间的关系，来预测待测样本的函数值，其优势在于不仅能够给出预测值，而且能够提供预测方差，以评估模型预测的不确定性。克里金模型不仅灵活性高，且能够很好地平衡其计算精度与计算效率，因而被广泛地用以代理隐式函数的模型[13-15]。

为了快速预测聚能装药的射流速度，本研究以Matlab为平台构建了自适应克里金代理模型，以炸药爆速、药型罩锥角和药型罩壁厚作为输入，以聚能射流速度作为输出，通过自学习方法，获得了预测精度较高的克里金模型。该模型可以实现对金属射流速度快速、准确地预测，以用于指导聚能装药的理论设计。应用LS-DYNA有限元软件[16-19]对所设计的聚能装药结构进行模拟，得到其射流速度，将相应参数下获得的数值计算结果与克里金模型的预测结果进行误差分析，以验证克里金代理模型的预测精度。

1 克里金代理模型的基本理论

(1)

其中h(x)=[h1(x),h2(x),…,hp(x)]T表示关于x的回归模型，可取0阶、1阶、2阶多项式；β=[β1,β2,…,βp]T为回归参数向量；p的取值如下：

(2)

z(x)是均值为0的稳态高斯过程，其协方差为：

cov(x(k1),x(k2))=σ2Rθ(x(k1),x(k2))

(3)

式中：x(k1)和x(k2)表示样本的两个实现值；σ2和Rθ(x(k1),x(k2))分别为稳态高斯过程z(x)的方差和相关函数。本研究使用如下的相关函数：

(4)

其中θi(i=1,2,…,n)是参数。

根据克里金模型的理论，可得回归参数向量β和稳态高斯过程z(x)的方差σ2如下：

(5)

(6)

式中：F为回归矩阵，其元素为Fji=hi(x*(j))(j=1,2,…,N*;i=1,2,…,n)；R为相关矩阵，其元素为Rl1l2=Rθ(x*(l1),x*(l2))(l1,l2=1,2,…,N*)。

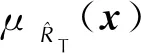
(7)

(8)

其中r(x)=[Rθ(x,x*(1)),Rθ(x,x*(2)),…,Rθ(x,x*(N*))]T且u(x)=FTR-1r(x)-h(x)。

2 聚能装药射流速度的数值计算

本研究利用LS-DYNA有限元软件，对锥角2α分别为46°、50°、60°，罩壁厚δ为1.1、1.2、1.3mm，使用B炸药、RDX基炸药和HMX基炸药的27个聚能装药模型形成的射流进行模拟计算，获得射流形态表征参数以及射流速度。

2.1 聚能装药结构

采用直径Ф50mm的聚能装药，其结构由药型罩、炸药装药、传爆起爆装置三部分组成，药型罩采用紫铜材料，装药结构长径比大于1.5，如图1所示。

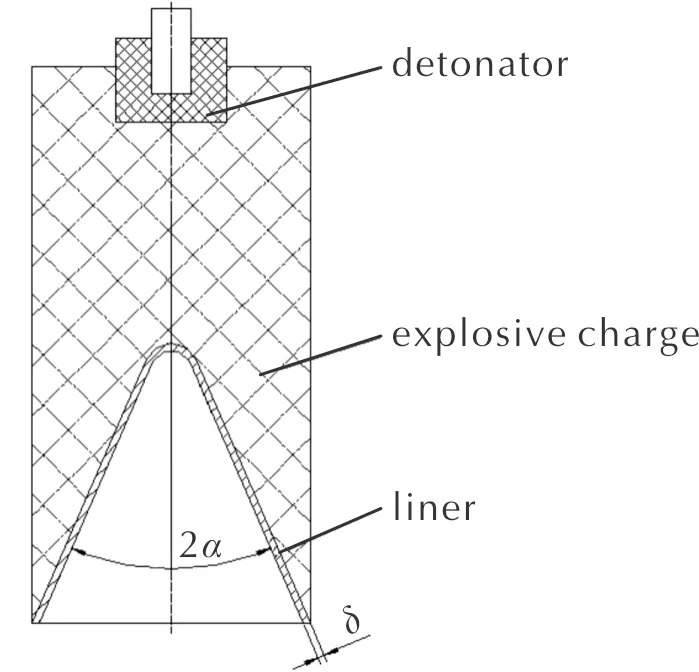
图1 聚能装药结构Fig.1 Schematic diagram of the shaped charge

2.2 计算模型建立及参数

利用LS-DYNA有限元软件，针对射流成型问题的特性，采用Euler网格建立包含药型罩、炸药和空气介质三部分的数值模型，采用多物质ALE算法来模拟炸药爆轰、药型罩压垮及射流形成过程。其中，炸药装药均采用关键字*MAT_HIGH_EXPLOSIVE_BURN材料模型和JWL状态方程进行描述，B炸药、HMX基炸药以及RDX基炸药装药的密度分别为1.72、1.81和1.70g/cm3，其爆轰性能参数和JWL状态方程参数见表1。紫铜药型罩采用弹塑性材料模型和Gruneisen状态方程描述[20]。空气介质用NULL材料模型以及LINEAR_POLYNOMIAL状态方程，空气密度取1.293×10-3g/cm3。

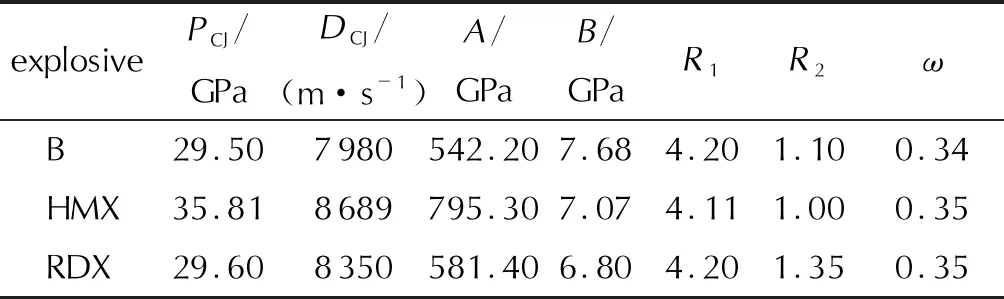
表1 炸药爆炸性能参数Table 1 Parameters of the explosives

2.3 数值计算结果

以1.1mm厚度药型罩为示例，分别采用B炸药、HMX基炸药、RDX基炸药为装药，不同锥角药型罩在起爆后40μs的模拟结果分别如图2所示，可以看到，对于同一种炸药装药，起爆后的射流伸长随锥角的增大而减小；炸药能量提高后，射流长度明显增加。表2为数值计算得到的射流性能参数。

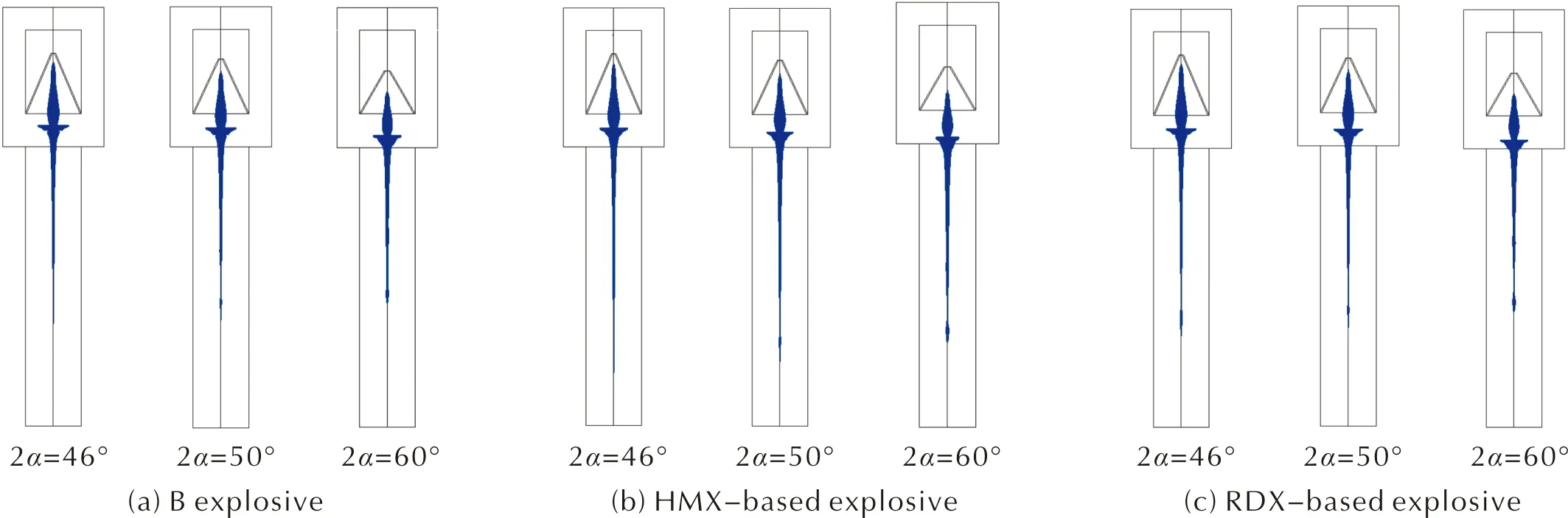
图2 炸药在不同罩锥角下形成的射流计算形态Fig.2 Forms of jet produced by the explosives under different cone angles

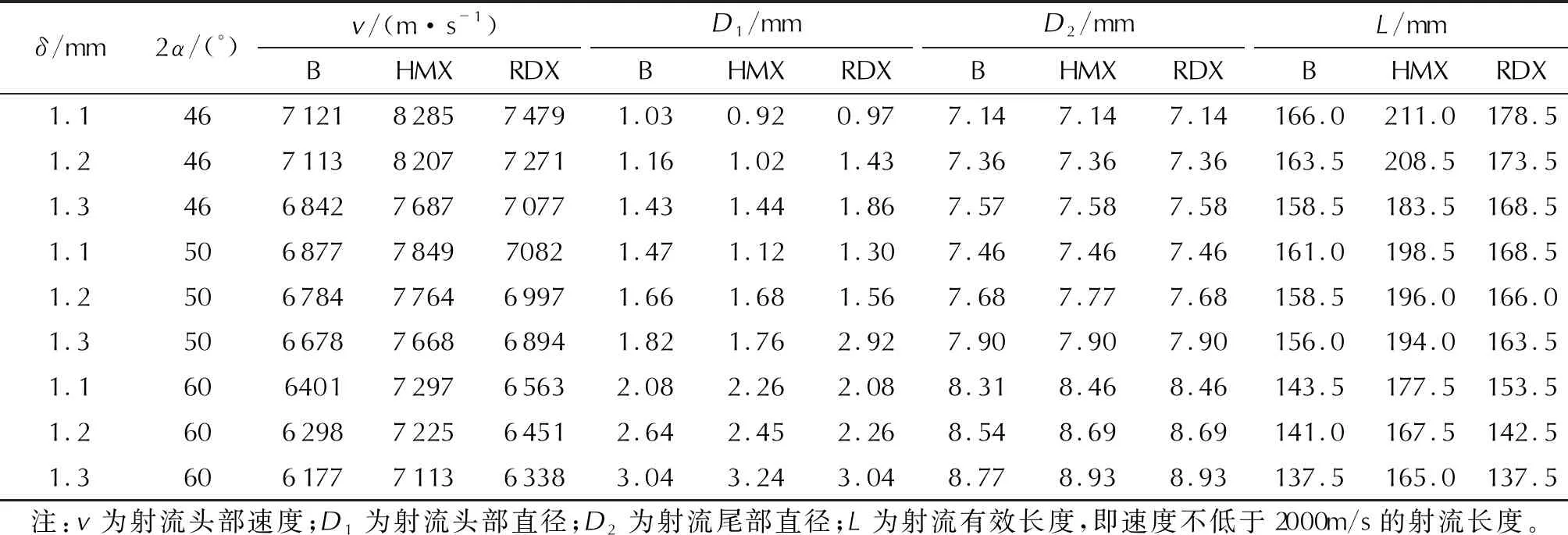
表2 炸药不同锥角时射流计算参数Table 2 Jet parameters of the explosives under different cone angles

由上述计算结果可以看出，在同一种炸药装药中，锥角不变的情况下，随着药型罩厚度增大，射流头部速度降低，头部直径、尾部直径增大，有效长度减小；药型罩厚度不变的情况下，随着锥角的增大，射流头部速度降低，头部直径和尾部直径增大，有效长度减小。对比3种炸药装药的结果，炸药能量的提高可以增大药型罩的爆炸载荷，从而提高射流速度和长度。

2.4 自适应克里金模型预测射流速度

表征射流性能的参数包括射流速度、长度以及速度梯度等都可以通过数值模拟计算来获取，但其计算时间成本仍然较高。为了快速预测聚能装药在不同炸药和不同药型罩结构下的性能参数，以射流头部速度为例，以炸药爆速、药型罩锥角、药型罩壁厚作为输入，射流头部速度为输出，建立克里金模型，实现射流头部速度的准确预测。此外，为了实现样本的有效利用，采用克里金标准差作为学习函数，在每次迭代时自动加入最优训练样本，以自适应更新克里金模型。该模型预测射流头部速度的流程如图3所示，具体过程如下：

(1)以炸药爆速、药型罩锥角和药型罩壁厚作为输入，记为xi(i=1,2,…,N)，N为样本个数(本研究中N=27)，建立样本池S(x);

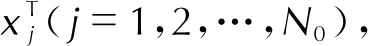
(3)判断克里金模型的收敛性。计算样本池中所有样本的预测值μgk(xi)以及克里金标准差σgk(xi)，找到标准差的最大值，如公式(9)所示：

(9)

如果σmax<σ*(本研究中取σ*=10-3)，则克里金模型收敛，μgk(xi)即为样本xi的克里金预测值；

(4)如果σmax≥σ*，利用学习函数选取下一个样本，加入训练集T，如公式(10)所示：

(10)

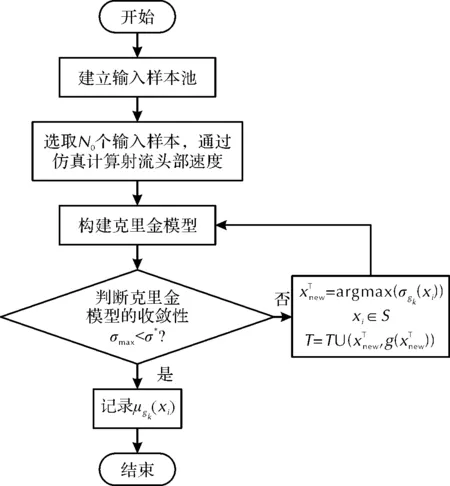
图3 自适应克里金模型的流程图Fig.3 The flow chart of the adaptive Kriging model

本研究在27组样本中随机选取5组作为初始训练样本，并利用LS-DYNA计算其射流头部速度。在训练克里金模型的过程中，根据公式(10)选取新的训练样本，当27组样本中的最大克里金标准差为5.38×10-4时，克里金模型收敛，则停止计算，最终训练样本的个数为11。为了验证该模型的计算精度，对测试样本进行了模拟计算，并计算了模拟结果与克里金模型预测结果的相对误差，其结果如表3所示。

由表3的计算结果可知，通过对聚能射流速度模拟结果与克里金模型预测结果进行相对误差分析，其最大误差不超过2%，可知克里金模型预测值与模拟计算结果吻合较好，表明克里金模型预测聚能射流速度时具有较高的准确度。在实际计算中，只需要11组样本的数值计算结果，并利用克里金模型，即可获得测试样本的射流速度，即通过11次数值模拟获得了27组样本的射流速度结果，其计算效率大幅提高。需要说明的是，射流长度等可以用单个参数表征的射流性能也可通过本研究的方法类似计算，这里不再赘述。

3 结 论

(1)所建立的自适应克里金模型可用于快速预测聚能装药射流速度，与有限元模拟结果相比，两者误差小于2%，表明克里金模型对射流速度计算具有较高的准确度。

(2)克里金模型能够用少量的计算成本，获得聚能装药射流速度，使得计算效率大幅提升，该方法提供了一条有效的技术途径，可用于指导聚能装药研究和理论设计。