SIDH 公钥压缩中双线性对的有效计算*

朱屹霖 李梦东 王 颖

北京电子科技学院，北京市 100070

引言

后量子密码是当前公钥密码学研究的一个热点。 自2011 年Jao 和De Feo[1]提出超奇异同源密码交换协议(SIDH)以来，基于同源的密码方案受到了关注。 由SIDH 改造的超奇异同源密钥封装(SIKE)协议，目前已成为NIST 后量子密码算法评选的第三轮九种密钥封装机制之一。与其他后量子协议相比，基于同源的协议具有较小的公钥。 而SIDH 还可以对公钥进行压缩，使SIDH 协议更具竞争力。 SIDH 是同源密码的基本类型之一，其他基于同源的身份认证、加密和数字签名等方案多是在其基础上的构造。 同源密码的密钥和密文(或签名)是几种后量子密码类型中长度最短的，但是也存在计算时间长的弱点，约是其他后量子算法的几倍时间。 因此如何提高计算速度，是SIDH 类型密码的研究重点之一。

SIDH 公钥压缩是将公钥的点表示为挠基分解，传输这一分解的系数，从而进一步减少公钥长度。 压缩过程一般分为三步:挠基分解、双线性对计算和求解离散对数。 SIDH 公钥压缩的思路由R. Azarderakhsh 等人[1]在2016 提出，将原来的公钥长度由6log2p减小到4log2p左右(p 是工作域的特征)，但公钥压缩时间花费是整个SIDH 计算时间的十倍；2017 年Costello 等人[2]进一步改进，通过将点P 和Q 进行正规表示，将公钥进一步压缩为3 个Zn元素，最终密钥大小近似3.5log2p， 并使公钥压缩的时间减小为与SIDH 密钥协商的时间相当。 同年Zanon 等[3]提出纠缠基算法，进一步提高了压缩性能。

本文主要在之前学者的工作基础上进一步优化，将重点放在双线性对计算上，对Miller 算法中线函数的部分信息采取预计算，以减少Miller 循环中消耗的计算成本。 与之前的工作相比，进一步提高了双线性对计算这一步的效率。

1 预备知识

1.1 椭圆曲线

令q=pn，椭圆曲线E/Fq是一个亏格为1的光滑射影代数曲线(至少有一个点)。 其仿射部分满足Weierstrass 方程:

另外它还有一个无穷远点O。 如果p≠2，3，则上述方程可同构为短的Weierstrass 方程y2=x3+a4x+a6。 判别式4a34+ 27a26 ≠0 且在Fq内。

1.2 超奇异椭圆曲线

如果椭圆曲线EFpm(p为素数) 满足以下等价的任何一个条件，就称它为超奇异椭圆曲线，否则就称之普通的椭圆曲线。

1.3 同源

设E1和E2是有限域Fq上的椭圆曲线。 同源φ:E1→E2是定义在Fq上的一个非平凡的保持基点的有理映射，也是从E1(Fq) 到E2(Fq) 的群同态。 如果存在这样的映射，就称E1和E2是同源的，两条曲线E1和E2在Fq上是同源的当且仅当＃E1(Fq)= ＃E2(Fq)。

同源φ可以用两个Fq上的有理映射f和g表示，即φ((x，y))= (f(x)，y·g(x))， 其中f(x)=p(x)/q(x)，多项式p(x) 和q(x) 在Fq上没有公因式，g(x) 也是如此。 同源的次数deg(φ) 定义为max{deg(p(x))，deg(q(x))}，其中p(x) 和q(x) 分别是f和g的分子与分母多项式。 仅用同源结构的f(x) 分量进行同源计算通常是很方便的。 给定同源φ:E1→E2，我们定义φ的核如下:ker(φ)={P∈E1:φ(P)=O}。

对于E(Fp) 的任意有限子群H， 存在唯一的同源φ:E→E′，使得ker(φ)=H，deg(φ)=|H|，其中|H| 表示H的基数。 在这种情况下，我们用E/H表示曲线E′。 给定一个子群H⊆E(Fp) 为例，利用Vélu 公式可以求出同源φ和同源的曲线E/H。

1.4 SIDH 协议

SIDH 协议过程为:Alice 随机选择mA∈Z/2e2Z，计算同源2e2-φA:E6→EA， 核为KA∶= ＜PA+ [mA]QA ＞， 并计算出φA(PB)，φA(QB) 和像曲线参数A，将(φA(PB)、φA(QB)、A) 发给Bob。 同样Bob 随机选择mB∈Z/3e3Z，计算同源3e3-φB:E6→EB，核为KB∶= ＜PB+[mB]QB ＞， 并计算出φB(PA)，φB(QA) 和图像参数B，将(φB(PA)、φB(QA)、B) 发给Alice。

Alice 收到消息后，计算同源φ′A:EB→EAB，核为＜φB(PA)+[mA]φB(QA)＞；B 也相同，计算同源φ′B:EA→EBA， 核为＜ φA(PB)+[mB]φA(QB)＞。 至此，由于EBA≅EAB，A 和B可用EBA和EAB的j-不变量得到共享密钥。

1.5 SIDH 的公钥压缩

以Alice 端为例，所谓的公钥压缩即压缩上述的(φA(PB)、φA(QB)、A)。 实际在SIDH 协议中，Alice 利用PA、QA、RA=PA-QA、RB=PB-QB的x 坐标和她的密钥来完成密钥生成的整个过程。 在这种情况下，Alice 应该向Bob 发送三元组(xφA(PB)，xφA(QB)，xφA(RB))。 同样方式也适用于Bob。 R. Azarderakhsh 等人[1]在2016 年提出将φA(PB)、φA(QB) 展开为挠基的表示，用其系数表示相应的点，从而实现了公钥的进一步压缩。

2 已有算法分析

R. Azarderakhsh 等人[1]的具体方法如下，以Alice 端为例。 其主要思想是实现一个确定性伪随机数发生器，找出一个3e3-挠基(UA，VA)，将φA(PB)、φA(QB) 表示为:

这时，Alice 可以通过用Pohligh-Hellman 算法求解阶为3e3的乘法子群中的离散对数来恢复a0，b0，a1，b1。 那么Alice 可以将(a0，b0，a1，b1，A) 作为自己的公钥分发给Bob，而不是(xφA(PB)，xφA(QB)，xφA(RB))。

同年Zanon 等人[3]提出纠缠基技术，加快了挠基的生成，并在双线性对计算这一步利用纠缠基产生的点对的特殊形状优化Tate 对，并在最后提出计算离散对数的高效方法，进一步减少了SIDH 压缩和解压缩的运行时间。

具体方法即在线性表示的基础上进一步优化。 由于＜ φA(PB)，φA(QB)＞=EA[3e3]，即φA(PB)，φA(QB) 也能构成EA[3e3] 中的一组基。 可以看出上述矩阵是可逆的，因此

这样做的好处是可以预先计算出h0的值，从而提高求解四个离散对数的效率。

2019 年M. Naehrig 和J.Renes[5]采用了对偶同源技术，显著降低了压缩的成本。 具体操作为，利用同源和其对偶的关系式，将上述除h0以外的四个对变换成如下形式:

在后面的计算就可以通过预存储第一个参数的所有信息以便加快后面的计算，但此方法需要对固定的系统参数进行大量的预计算，尽管它在速度上有了显著的提升，而存储双线性对计算和离散对数解的表需要很大的存储空间，对内存造成一定的影响。

2021 年Kaizhan Lin 等学者[6]也采用了对偶同源技术，提出了新的改进，从函数除子之间的迭代关系进行优化，推导出许多关系式，提出了几种提高双线性对计算效率的算法，不仅减少了计算成本，而且节省了近四分之一的内存来存储预计算。

3 改进的算法

双线性对计算是公钥压缩的计算瓶颈。 双线性对计算过程就是线方程的迭代。 对于公钥压缩中这一步的改进，许多方法大多延续和修改线方程的公式，而预计算通过提前计算和存储相关结果可提高计算效率。 因此本文在Costello等人[2]的工作基础上进一步改进，预先存储相应的Miller 算法中P 的倍点及线函数的部分信息，以提高后续Miller 迭代的效率。

Costello 等人[2]在仔细检查了二倍线函数和三重抛物线运算的显式公式之后，选择使用坐标元组(X2:XZ:Z2:YZ) 代表中间射影点P=(X:Y:Z) 以提高域算术的运算效率。 在本文使用这种表示且满足XYZ≠0，因为它们的阶数严格大于2，这确保了下列公式不包含例外情况。

那么我们观察可得，上述5 个系数的显式公式中出现许多相同的项，如果每次Miller 迭达都重复计算，会大大降低计算效率，因此可以预先计算以下所有值:

算法1:点P 的二倍运算输入:(U1，U2，U3，U4)输出:(V1，V2，V3，V4)1 V1 ←t22，2 V2 ←4t3·t2，3 V3 ←16t32，4 V4 ←2t5·(t2 + 2U2·(4U2 + A(U1 + U3))).

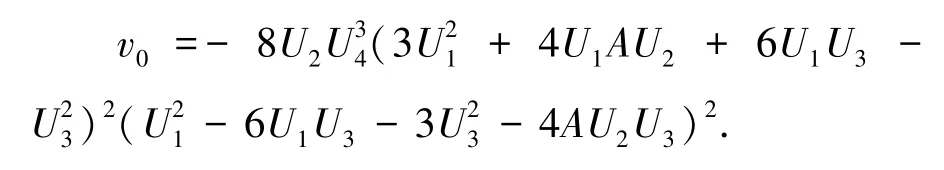
同样观察可得，如果预先计算以下所有值，线函数的计算效率会有所提高:

算法2:点P 的三倍运算输入:(U1，U2，U3，U4)输出:(V1，V2，V3，V4)1 V1 ←U1·t0·t52，2 V2 ←t6，3 V3 ←t7，4 V4 ←8U3·t1·t8·(16A2s1s3 + 28As0s4+ 28As3s4 + 4As2s4 + 4As0s5 + 6s32 + 28s0s3+ s22 + 28s2s3 + s02)·(U3 + U1 + AU2)2

通常情况下，我们用M，S 分别表示Fp2中的乘法运算和平方运算，定义一个二次扩域元素大小为log pbit。

未改进之前，Costello 等人[2]的方法在计算上述阶为2eA的Tate 对的情况下，在二次扩域中每次计算二倍-线函数的成本为9M+5S； 阶为3eB的Tate 对的情况下，在二次扩域中每次计算三倍-抛物线函数的成本为19M+6S。

改进之后，本文方法在计算阶为2eA的Tate对的情况下，每次需要预计算5 个元素，约需存储空间大小为5log pbit，在二次扩域中二倍-线函数相应的计算成本为7M+2S， 相对节省2M+3S；阶为3eB的Tate 对的情况下，每次需要预计算15 个元素，约需存储空间大小约为15log pbit，在二次扩域中三倍-抛物线函数相应的计算成本为14M+5S，相对节省5M+S。

4 结束语

SIDH 公钥压缩是进一步减少公钥长度的措施，如何减少公钥压缩带来的负面影响(即计算代价大)是同源密码研究的热点问题。 值得注意的是Miller 算法中线函数的计算不仅是配对计算的主要瓶颈，也是整个公钥压缩的瓶颈。 本文主要针对SIDH 中公钥压缩过程中的Miller 计算，提出了有效提高配对计算的方法，从而减少整个公钥压缩过程的计算时间。