团簇NiPS3 光谱性质的密度泛函分析

宋静丽 方志刚 毛智龙 井润田 曾鑫渔 刘立娥

(辽宁科技大学 化学工程学院, 鞍山 114051)

引 言

随着现代社会的飞速发展,各种新型材料层出不穷。 2004 年,曼彻斯特大学Geim 小组成功分离出单原子层的石墨材料——石墨烯[1],此后,以石墨烯为代表的二维原子晶体材料开始出现在人们的视野中。 二维材料由于具有优异的光学[2]、电学[3-4]、力学[5]、异构性[6]等性质,在材料学[7]、微纳加工[8]]、能源[9]和生物医学[10]等领域具有广阔的应用前景,促使科研人员在凝聚态物理学中对其进行广泛的研究。

近年来,过渡金属磷酸盐(MPTs)材料[11]作为一种新型的二维材料,引起了人们的广泛关注。MPTs 材料不仅具有二维材料的众多优点,而且由于金属与非金属的耦合而展现出独特的能带和电子结构,具有优异的光学、催化、电子和磁性等物理化学性质。 二维层状晶体NiPS3作为众多过渡金属磷酸盐材料的代表[12],由于具有诸多优良的性能而逐渐成为研究热点。 Ismail 等[13]通过固相反应在真空硅管内培养出单相NiPS3,发现NiPS3化合物呈层状单斜结构,这种结构允许粉末在其面间空间储存氢,证实了NiPS3材料具有可行的储氢能力。 Xue 等[14]制备了NiPS3纳米片-石墨烯(NiPS3-G)复合材料,发现由于协同效应,其电催化析氧反应(OER)的性能更高且更稳定,综合性能远远优于2D 材料,甚至优于许多传统材料,这揭示了NiPS3-G 复合材料可以作为高效OER 电催化剂。 Liu 等[15]制备了少层NiPS3纳米薄片,对其进行锁模光纤激光器评估和表征,揭示了NiPS3纳米薄片具有非线性光学特性,表明NiPS3材料具有应用于光子学领域的潜能。 Suto等[16]合成了亚微米级NiPS3粒子,并将其作为硫化基全固态锂电池的正极活性材料,研究了其电化学性能,发现NiPS3尺寸的减小可以提高其自身的电化学性能,表明NiPS3是一种高性能的全固态锂电池活性材料。

光谱学性质是一种适用于光电子应用的基础特性[17],近年来,不乏对NiPS3晶体的光谱学如红外和拉曼光谱的研究。 Neal 等[18]基于同步辐射的近场红外纳米光谱,研究了MPS3(M =Mn,Fe,Ni)系列材料的对称交叉,发现这类材料的单斜性是长程堆积、温度效应和局部晶格畸变的结果。 Chu 等[19]对不同基底上的不同纳米片进行了拉曼光谱分析,发现拉曼光谱强度与材料厚度之间存在线性关系;此外,他们利用少层二维NiPS3纳米片制备了紫外光探测器,其性能优于传统的宽带隙紫外探测仪,从而为NiPS3纳米片应用于超快紫外光检测奠定了基础。 Kuo 等[20]利用机械剥离法首次成功分离出单层和多层复合NiPS3样品,发现NiPS3的层数影响其拉曼光谱的表征,NiPS3薄片的拉曼光谱与本体材料有很大的不同,并且不同层数的NiPS3薄片的拉曼光谱差异很大。

不难看出,对于NiPS3材料进行的光谱学分析均基于层状晶体材料NiPS3。 由于NiPS3单层薄膜暴露在环境大气中,在采集到拉曼光谱和红外光谱之前,薄膜就可能发生了降解。 而且,目前利用传统的红外技术剥离样品的方法并非适用于所有复杂的硫族化合物,尤其是NiPS3材料,因此对NiPS3材料的光学性质的分析受到了限制。 为了弥补这一缺陷,本文以团簇NiPS3为局域模型,模拟了单层过渡金属磷酸盐材料NiPS3的微观结构组成,并基于密度泛函理论,从红外光谱、偶极矩、拉曼光谱和极化率方面对其光谱学性质进行分析,以期得到其结构特征和规律,为后续实验研究提供一定的理论支撑与参考。

1 模型设计与计算方法

1.1 理论模型设计

以拓扑学原理为理论基础对团簇NiPS3进行分析,以平面五边形、四棱锥和三角双锥为基础构型,通过改变不同原子间的相对位置,设计出团簇NiPS3在二、四重态下的初始构型。

1.2 计算方法

基于密度泛函理论[21-22]中的 B3LYP 杂化[23-24],使用def2-tzvp 基组对团簇NiPS3的所有初始构型在二、四重态下进行全参数优化计算,得到可以稳定存在的优化构型。 优化收敛条件为:最大作用力小于0.000 45,均方根作用力小于0.000 30,最大位移小于0.001 80,均方根位移小于0.001 20,其中对P 和S 加极化函数。 以上所有的运行计算和数据处理过程均在HP-Z440 计算机上利用Gaussian09 程序完成,并使用洛伦兹函数L(ω)(式(1))对通过优化计算和频率分析得到的稳定构型进行数据分析和处理,以此绘制出团簇NiPS3各优化构型连续的红外光谱图和拉曼光谱图。

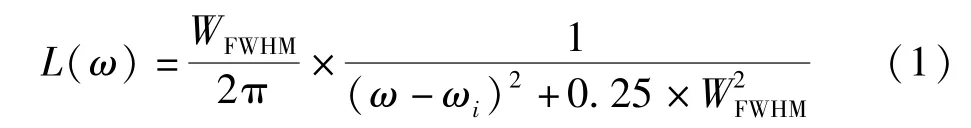
式中:WFWHM为半高全宽(8 cm-1),ω为波数,ωi为跃迁能量。

2 结果与讨论

2.1 优化构型

对团簇NiPS3初始构型进行优化计算并排除虚频及相同构型后,共得到9 种可稳定存在的优化构型。 以能量最低的构型1(2)为基准(设其能量为0 kJ/mol),对其他构型的能量重新计算后得到其相对能量,并按照相对能量由低到高的顺序对优化构型排序,结果如图1 所示。

由图1 可以发现,在团簇NiPS3的优化构型中,二重态构型有4 种,四重态构型有5 种,并且团簇NiPS3的所有优化构型都呈C1 对称。 团簇NiPS3优化构型的几何形态为平面五边形型(构型1(2)和4(2))、三角双锥型(构型1(4)和2(2))、戴帽三角锥型(构型3(4)、4(4)、5(4)和5(2))、四棱锥型(构型2(4))。由以上分析不难看出,平面形构型仅存在于二重态,说明团簇NiPS3的平面形在二重态下更容易稳定存在。 比较各优化构型的相对能量大小可知,构型1(2)的相对能量最小,相较其他优化构型更为稳定,而构型1(2)与文献[18 -20]所报导的NiPS3结构同为平面型,并且与Kuo 等[20]报道的单层NiPS3结构极为相似。

图1 团簇NiPS3的优化构型图Fig.1 Optimized configuration diagrams of the NiPS3 cluster

2.2 团簇NiPS3的红外光谱分析

2.2.1 红外光谱图

当体系满足入射红外光子能量与发生振动跃迁时所需的能量相等,且红外光与体系分子间产生耦合时,体系便表现出红外活性。 在产生红外活性时,含有不同原子个数的体系由于分子自由度的不同,其理论振动峰的数目也不同。 对于非线性分子体系团簇NiPS3而言,在产生红外活性时,理论上有9 个红外吸收振动峰,图2 为由团簇NiPS3各优化构型的红外数据拟合得到的红外光谱图。

由于发生谱带简并,吸收峰的数量会少于振动自由度。 观察图2 可得,构型1(2)有7 个振动峰,构型1(4)有5 个振动峰,构型2(2)有5 个振动峰,构型2(4)有4 个振动峰,构型3(4)有4 个振动峰,构型4(4)有5 个振动峰,构型5(4)有6 个振动峰,构型4(2)有5 个振动峰,构型5(2)有4 个振动峰。 各个优化构型的吸收峰数量与振动自由度均不相等,说明在团簇NiPS3的各优化构型中均发生了谱带简并。 例如,在最稳定的构型1(2)中有2 个振动峰被简并:波数为181.35 cm-1的振动峰,其振动形式为P2-Ni1-S4 键和S3 - Ni1 - S5 键的面外摇摆振动; 波数为279.75 cm-1的振动峰,其振动形式为Ni1-S5-S3 键和P2-S5-S4 键的面内剪式振动。 结合图2 及相关计算数据对团簇NiPS3各优化构型的红外特征峰振动形式进行分析,发现构型1(2)的特征振动峰的分布趋势为右侧的峰大,中间和左侧的峰较小,其中最高峰的波数为591.02 cm-1,振动形式为P2-S4-S3键的面内剪式振动;次高峰的波数为454.54 cm-1,振动形式为P2-Ni1-S4 键的面内剪式振动。 构型1(4)的特征振动峰的分布趋势为两边的峰小,中间的峰大,其中最高峰的波数为352.32 cm-1,振动形式为S3-S4-S5 键的对称伸缩振动和Ni1-S3-P2 键的面内摇摆振动;次高峰的波数为411.63 cm-1,振动形式为S3- S4- S5 键的非对称伸缩振动和P2-Ni1-S4 键的面外摇摆振动。 构型2(2)的特征振动峰主要分布在右侧,中间和左侧的峰较小,其中最高峰的波数为451.65 cm-1, 振动形式为P2-Ni1-S4 键的面内剪式振动和S4-Ni1-S5 键的面内摇摆振动;次高峰的波数为343.55 cm-1,振动形式为P2-Ni1-S5 键的面内摇摆振动和S3 -Ni1 -S4键的对称伸缩振动。 构型2(4)的特征振动峰的分布趋势为从右到左依次减小,其中最高峰的波数为600.43 cm-1,振动形式为P2-Ni1-S3 键的面内剪式振动;次高峰的波数为555.56 cm-1,振动形式为Ni1-S5-S3 键的面外摇摆振动和P2-S5-S4 键的面内剪式振动。 构型3(4)的特征振动峰的分布趋势为右侧的峰最大,左侧的峰次之,中间的峰最小,其中最高峰的波数为643.41 cm-1,振动形式为P2-S4-S5 键的非对称伸缩振动; 次高峰的波数为345.44 cm-1,振动形式为Ni1-P2-S5 键的面外摇摆振动和S3-Ni1-S4 键的对称伸缩振动。 构型4(4)的特征振动峰的分布趋势为从右到左依次减小,其中最高峰的波数为496.93 cm-1,振动形式为P2-S4-S3 键的面内剪式振动; 次高峰的波数为457.51 cm-1,振动形式为S4-Ni1-S5 键的伸缩振动。 构型5(4)的特征振动峰主要分布在右侧,中间和左侧的峰都较小, 其中最高峰的波数为508.63 cm-1,振动形式为S4-Ni1-S5 键和P2-Ni1-S3 键的剪式振动;次高峰的波数为461.86 cm-1,振动形式为整体变形的弯曲振动。 构型4(2)的特征振动峰集中分布在中间和右侧,其中最高峰的波数为570.27 cm-1,振动形式为S3-S4-P2 键的剪式振动;次高峰的波数为522.31 cm-1,振动形式为S4-P2-S5 键的剪式振动。 构型5(2)的特征振动峰集中分布在中间和右侧,右侧的峰最大,其中最高峰的波数为651.22 cm-1,振动形式为P2-S5-S3 键的非对称伸缩振动;次高峰的波数为369.86 cm-1,振动形式为Ni1-P2-S3 键的面外摇摆振动和S4-Ni1-S5 键的对称伸缩振动。

综合以上分析可得,构型5(2)和3(4)的红外特征振动峰的分布趋势相似,并且最高振动峰和次高峰的波数相近、振动形式相同,说明二者的红外活性相近。 构型2(2)和1(4)的最高峰的波数相较于其他同重态下优化构型的最高峰的波数均明显减小,都发生了红移现象。 构型5(2)和3(4)以及构型2(2)和1(4)为不同重态下几何形态相同的构型,说明构型的几何形态会对红外活性产生一定的影响。

2.2.2 偶极矩

偶极矩是一个矢量,定义为正负电荷中心的距离与电荷中心所带电荷量的乘积。 偶极矩可以在一定程度上显示分子中正电荷中心与负电荷中心的分离情况,从而表明分子的极性情况。 红外活性的产生是由于振动引起分子偶极矩或电荷分布发生变化,此时体系可吸收相应频率的红外光而产生红外活性,因此体系红外活性的强弱与偶极矩的大小密切相关。 偶极矩的大小可以在一定程度上体现体系红外活性的强弱:偶极矩越大,红外活性越强;偶极矩越小,红外活性越弱。 为了比较团簇NiPS3各优化构型的红外活性,按照式(2)计算总偶极矩μtotal,结果列于表1 中。

式中:μx、μy、μz分别为x、y、z轴的偶极矩分量。

由表1 可以看出,几何形态为平面五边形的构型1(2)和4(2)的x轴和y轴的偶极矩相近并且均大于z轴的偶极矩,说明其红外活性主要来源于x轴和y轴;几何形态为三角双锥型的构型1(4)和2(2)的z轴偶极矩相近,并且均是z轴对总偶极矩的贡献最大,说明其红外活性主要来源于z轴。 由此也验证了2.2.1 节中所得的结论:构型的几何形态会对红外活性产生一定的影响。 进一步对总偶极矩数据分析可得,在二重态的优化构型中,构型5(2)的总偶极矩最大;在四重态的优化构型中,构型3(4)的总偶极矩最大,并且与构型5(2)的总偶极矩大小相近,验证了2.2.1 节中的结论:构型5(2)和3(4)的红外活性相似。

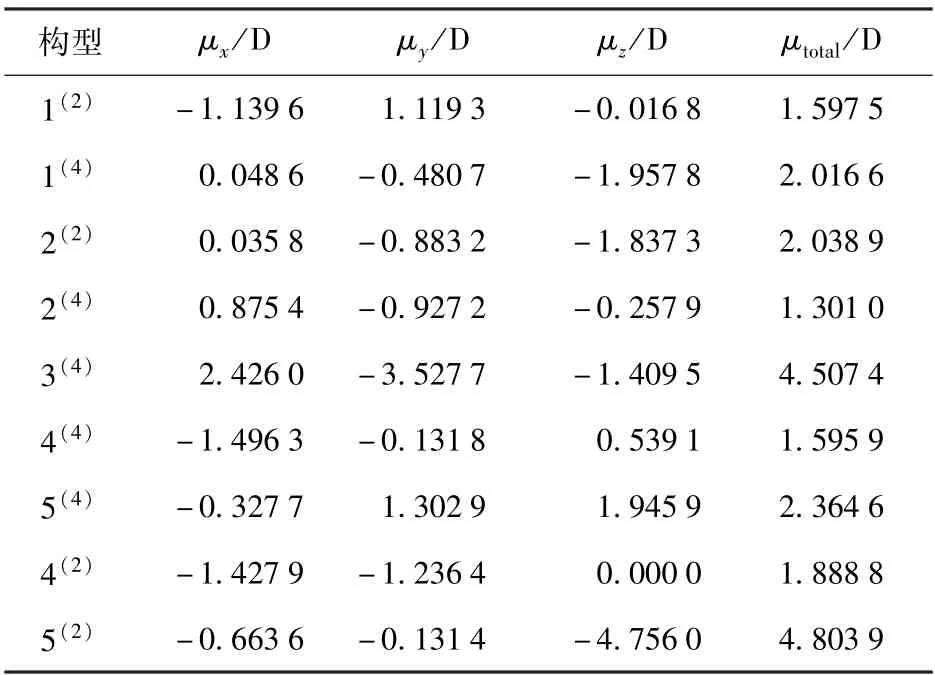
表1 团簇NiPS3各优化构型的偶极矩Table 1 Dipole moments of optimized configurations of the NiPS3 cluster

2.3 团簇NiPS3的拉曼光谱分析

2.3.1 拉曼光谱图

拉曼光谱是一种应用广泛的光谱学表征工具[25-26],主要用于大块和剥离的二维原子晶体材料,如石墨、石墨烯和过渡金属硫族化合物光学性质的测定与分析。 与作为吸收光谱的红外光谱不同,拉曼光谱作为一种散射光谱与体系的极化率有着密切的联系。 红外光谱为波数非负的连续谱图,而拉曼光谱存在反斯托克斯散射区(波数为负的区域)、瑞利散射区(波数为0 的区域)和斯托克斯区(波数为正的区域),为了方便对NiPS3的拉曼光谱进行研究,将反斯托克斯区域略去,只研究瑞利散射区和斯托克斯区。 图3 为绘制出的团簇NiPS3各构型的拉曼光谱图。

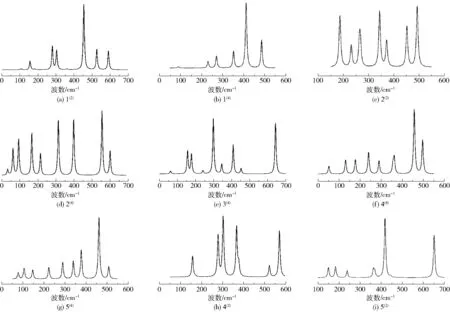
图3 团簇NiPS3各优化构型的拉曼光谱图Fig.3 Raman spectra of optimized configurations of the NiPS3 cluster

由图3 可得,构型1(2)有6 个特征振动峰,分布趋势为中间的峰大、两边的峰小,其中最高峰的波数为454.54 cm-1,振动形式为P2-Ni1-S5 键的面内剪式振动和S3-Ni1-S4 键的面内摇摆振动;次高峰的波数为279.75 cm-1,振动形式为Ni1-S5-S3 键和P2-S5-S4 键的面内剪式振动。 构型1(4)有5 个特征振动峰,主要分布在右侧,其中最高峰的波数为411.67 cm-1,振动形式为S3-S4-S5 键的非对称伸缩振动和P2-Ni1-S4 键的面外摇摆振动;次高峰的波数为485.32 cm-1,振动形式为P2-Ni1-S3 键的非对称伸缩振动和S3-S4-S5 键的对称变形振动。构型2(2)有7 个特征振动峰,在中间和两侧都有分布且峰值均较大, 其中最高峰的波数为492.37 cm-1,振动形式为S3 -S5 -Ni1 键的面外摇摆振动和P2-Ni1-S4 键的非对称伸缩振动;次高峰的波数为343.55 cm-1,振动形式为P2-Ni1-S5 键的面内摇摆振动和S3-Ni1-S4 键的对称伸缩振动。构型2(4)有8 个特征振动峰,左侧和中间分布较为集中, 右侧的峰值最大, 最高峰的波数为555.71 cm-1,振动形式为Ni1-S5-S3 键的面外摇摆振动和P2-S5-S4 键的面内剪式振动;次高峰的波数为398.38 cm-1,振动形式为Ni1-S3-S5 键的面内剪式振动和S3-P2-S4 键的面内摇摆。 构型3(4)有7 个特征振动峰,分布趋势为中间和右侧的峰大、左侧的峰小,其中最高峰的波数为298.77 cm-1,振动形式为Ni1-S5-P2 键和S3-S4-S5 键的面内摇摆振动;次高峰的波数为643.56 cm-1,振动形式为P2-S4-S5 键的非对称伸缩振动。 构型4(4)有8 个特征振动峰,分布趋势为右侧的峰大、中间和左侧的峰小,其中最高峰的波数为457.51 cm-1,振动形式为S4-Ni1-S5 键的面内剪式振动和P2-Ni1-S3 键的面内摇摆振动;次高峰的波数为497.09 cm-1,振动形式为P2-Ni1-S3 键的面内剪式振动。 构型5(4)有9 个特征振动峰,分布趋势为右侧的峰大、中间和左侧的峰小,其中最高峰的波数为461.33 cm-1,振动形式为整体变形的弯曲振动;次高峰的波数为377.26 cm-1,振动形式为S3-S4-S5 键的面内摇摆振动和Ni1-S4-S3 键的剪式振动。 构型4(2)有6 个特征振动峰,分布趋势为中间的峰大、右侧的峰较小、 左侧的峰最小, 其中最高峰的波数为302.88 cm-1,振动形式为Ni1-S5-P2 键和S3-S5-S4 键的面内剪式振动; 次高峰的波数为366.64 cm-1,振动形式为P2-Ni1-S4 键的面内摇摆振动和S3-Ni1-S5 键的面内剪式振动。 构型5(2)有6 个特征振动峰,分布趋势为中间的峰最大、右侧的峰较小、左侧的峰最小,其中最高峰的波数为418.03 cm-1,振动形式为S4-Ni1-S5 键的面内摇摆振动;次高峰的波数为651.50 cm-1,振动形式为P2-S5-S3 键的非对称伸缩振动。

综合以上分析可知,构型4(2)和3(4)的最高峰的波数相较于其他同重态下优化构型的最高峰的波数均明显减小,都发生了红移现象。 由于构型5(2)和3(4)的拉曼光谱特征峰的分布趋势相近,次高峰的波数相近,最高峰和次高峰的振动形式相同,因此推测两者的拉曼活性相近。 结合图2 与图3 不难发现,对于团簇NiPS3的优化构型,在红外活性强的波数区域,优化构型的拉曼活性较弱,这验证了红外光谱和拉曼光谱的互补性,说明计算结果的准确性和可靠性。

2.3.2 极化率

拉曼散射是一种非弹性散射,散射来源于被探测物的某种物理性质的涨落,比如声子、自旋波和等离子等,描述这些涨落的量为极化率α。 分子在发生振动时,电子云分布或弥散程度的改变会使极化率也发生变化,从而使体系具有拉曼活性。 拉曼效应是分子极化率改变的结果,体系拉曼活性取决于分子振动时诱导偶极矩μ(μ=αE)的变化,在外加电场强度E一定的情况下,极化率越大,诱导偶极矩越大,即拉曼光谱的强度越大。 换言之,只要极化率不为零,分子振动模式就是拉曼光谱可见的。 按照式(3)计算团簇NiPS3各优化构型的极化率α,结果列于表2 中。

式中:αxx、αyy、αzz分别为xx轴、yy轴、zz轴的极化率张量。

由表2 可以看出,团簇NiPS3所有优化构型的极化率张量均集中在xx、yy和zz轴上,总体上xx轴的张量比yy轴稍大,比zz轴大很多。 进一步对数据进行分析,发现构型5(2)和3(4)的极化率张量分布相似,极化率大小相近,说明二者的拉曼活性相近,从而验证了2.3.1 节中对二者的拉曼光谱分析所得出的结论。 对于构型1(4)和4(2)、构型2(2)和4(4)、构型2(4)和5(2)而言,虽然极化率的大小相近,但是极化率张量和拉曼光谱图均相差较大,说明极化率张量大小是影响其拉曼活性的关键因素。

表2 团簇NiPS3各优化构型的极化率Table 2 Polarizabilities of optimized configurations of the NiPS3 cluster

3 结论

本文以密度泛函理论为理论基础,在较高量化水平下,对团簇NiPS3的红外光谱、偶极矩、拉曼光谱和极化率进行了光谱学性质分析,得到如下结论:

(1)团簇NiPS3的所有优化构型均为C1 对称,其中二重平面非对称构型1(2)的能量最低,相较于其他构型更加稳定。

(2)二重立体戴帽三角锥构型5(2)和四重立体戴帽三角锥构型3(4)的红外特征振动峰与拉曼特征振动峰的分布趋势相似,最高振动峰及次高峰的振动形式相同,红外最高振动峰及次高峰的波数相近,拉曼次高峰的波数相近,并且两种构型的总偶极矩大小相近,极化率张量分布相似,极化率大小相近,说明二者的红外活性和拉曼活性均相近。

(3)二重立体三角双锥构型2(2)和四重立体三角双锥构型1(4)的红外振动最高峰的波数明显小于相同重态下其他优化构型最高峰的波数,均发生了红移现象;二重平面非对称构型4(2)和四重立体戴帽三角锥构型3(4)的拉曼振动最高峰的波数明显小于相同重态下其他优化构型最高峰的波数,均发生了红移现象。

(4)构型的几何形态会对团簇NiPS3的红外活性产生一定的影响;极化率张量主要集中在xx、yy和zz主轴,极化率张量大小是影响其拉曼活性的关键因素。