新课程背景下高中数学教学中学生解题能力的培养策略探究

张 菊

(江苏省南通市小海中学 226000)

新课程背景下的高考数学，导向学生的能力素养，最终指向学生对问题的解决能力的养成.高考中同学们要面对各种各样的问题，利用已有的知识素养，对问题展开积极地分析和思考，在积极的问题解决态度、品质等的引领下，学生在具体的学习实践中，才能够保持科学的态度、冷静的分析、开阔的思维.接下来，本文就以笔者的实际教学经验为例，谈谈高中数学学习中，解决问题能力的重要性，以及新课程背景下如何有效地培养学生的解决问题能力.

1 解决问题能力的重要性

纵观新课程改革的方向，可以发现高考命题的导向引领着课堂教学改革的方向.随着命题导向由知识向能力倾斜，能力素养在具体的教学实践中越来越被重视，解决问题能力是关系学生的学习和发展的重要能力之一.当然，解决问题能力不是一种单一的能力，需要学生通过对课堂学习的积累，在具体的学习实践中，培养和发展起来个各种能力素养.在具体的学习实践中，能够学会从个各种现象中抽象出数学问题，能够梳理出各种数学现象之间的逻辑关系，在对逻辑关系的具体分析和思考的基础上，对数学知识体系进行建模、分析、运算、想象等.在具体而生动的数学问题解决过程中，学生的问题分析、判断、推理等能力、学生的创新、实践、思维等，也能够得到有效地培养和发展.当然，这些能力的养成，并不是学生独立完成的，需要学生在具体的学习实践中，结合科学的信息技术媒体助力，与学生间的互助合作等途径来实现.解决问题能力的养成，不仅学生的学习中需要用到，学生的生活中更加需要这种能力.特别是在新的信息化时代，行业的竞争压力越来越大，学生的动手实践能力越高，在具体的实践过程中的问题解决力越强，他们就越能够受到行业的优待.社会需求和市场导向背景下的新时代教育，必须能够应对新时代的各种挑战，如果没有在学校教育情境中，训练过硬的问题解决的心理素质，就很难应对新时代的各种挑战和危机.

2 新课程背景下，高中数学教学中解决问题能力的培养策略

2.1 创设情境，激发兴趣

高中阶段的数学学习，其抽象性逻辑性更强，在面对一些数学推理性的问题时，如果学生的基础知识没有打牢固，在具体的学习实践中，对问题的分析、理解就会出现各种磕绊，这些小的磕绊会不断积累成为大的问题，让学生在长时间的问题积累中，不断积累对数学学习的负面情绪，在面对这类问题的时候，学生的参与性降低，甚至逐渐扩散到整个学科的学习实践中.特别是在逻辑分析的奠基时期，没有有效地问题引导和鼓励，学生在具体的学习实践中很难达到预定的学习目的.

例如，在学习《命题、定理、定义》时，教师利用教学，引入哥德巴赫猜想，提出世界近代三大数学难题之一即哥德巴赫猜想.在开门见山的叙述的基础上，引入猜想内容，1742年6月7日，哥德巴赫写信给当时的大数学家欧拉，提出了他们的观点：每一个大于2的偶数即是两个素数的和.如4=2+2，6=3+3，8=3+5…….同学们看到这个命题，你有什么感想呢？学生看到这个命题，给出的例子，确实很难反驳，但是，这个问题到现在为止，也没有得到正面的证明，也没有被推翻的命题.很多学生理所当然地说，这本来就是啊，就像1+1=2，这需要证明吗？有些东西不需要证明.但是恰恰相反，数学很多命题和定理都是需要经过证明才能判断真假的，中国著名的数学家陈景润，用了三年的时间证明了“1+2=3”，但是，全世界没有一个数学家证明“1+1=2”.用数学故事情境激发学生对数学逻辑推理的兴趣，在问题情境的驱动下，学生渴望对数学家们探索和研究的知识进行分析和思考，希望自己能够在问题分析和判断的过程中有所收获.他们在强烈的学习动机的支配下，积极自主地融入到对学习对象的探索和求知的实践中去.在对强烈的学习能动性的激励下，引导学生展开对命题的科学能动的认识.

2.2 巧设支架，科学建构

教学设计并不是要让学生在学习活动中仍然保持原有的水平，而是在原有得知识水平的基础上，“跳一跳，摘桃子”.建构学习支架，帮助学生构建认知框架，在科学的框架建构的基础上，引导学生开展积极的学习探索和实践.进入到高中阶段的数学知识学习，其复杂性程度更高，很多具有畏难心理的学生，就特别容易在面对一些复杂性、抽象性的问题的时候，轻言放弃.教师要把握学生的学习心理，在适当的时候，巧妙地为学生建构认识支架，帮助学生有效地理解和把握问题，在对问题的有效分析和理解的基础上，打通认识的关卡，突破思维的界限，在迸发的灵感和思路的引导下，展开积极的学习实践.

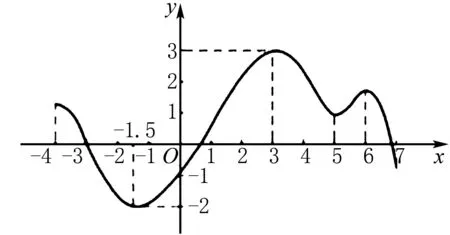
图1

例如，在学习《函数的单调性》时，很多学生在面对非常复杂的函数的取值分类的时候，特别头疼.看到这些问题就会因为惯性思维的作用，认为问题非常复杂，不好解决，所以就直接放弃不想做了.其实，学生并不是学不会，只是因为在学习过程中，没有因为他们没有唤醒心中已有知识经验对图示内容的联结，教师要创造性地为学生们搭建学习支架，将复杂的问题划分成一个个简单的小问题，通过对小问题的解析，让学生学会分步子理解和分析.划分区间，每一个区间内的函数的走向是一致的，通过对不同区间内函数的单调性的分析，就能够找到该函数在该取值范围之内所表现出的单调性，找到函数在该区间的最值.数学学习并不是要将问题复杂化，转化思想在具体的数学学习实践中的应用，能够帮助学生在面对问题的时候，主动地将复杂的问题简单化处理，在反复的经验积累和调动的基础上，学生积累了一定的问题转化的策略，在面对复杂的问题的时候，形成了惯性思维.解决问题的方法和思路在具体的问题转化过程中，变得简单而生动起来，学习的效能感和成就感也在学生们对问题的有效解决的基础上得到有效地满足.

2.3 生活思维，贴近体验

新课程背景下的高中数学教学中，学生解决问题能力的培养，需要通过多元的认知体验，为学生创设认识和理解问题的更加贴近生活、贴近实际的体验环境和氛围，让学生在积极能动的环境和氛围体验中，培养起用生活的视角和实践的思想来分析和解决问题的习惯.生活是最好的老师，学生习惯了运用生活眼光来展开对问题的分析和思考，他们的数学意识就能够得到有效地培养和发展.生活处处有数学，数学和学生们的现实生活息息相关，在这种生活学习思想的引领下，学生们会主动地将数学学习中的各种问题与现实生活有机地结合起来.

例如，在学习《平面向量》引入向量概念时，教师利用时事热点一，结合学生们生活中最关心的热点时事来吸引学生对数学的兴趣.近来乌克兰和俄国的战争十分激烈，中国公民在乌克兰的安全问题也已经成为全国关注的热点，中国已经发出撤侨航班，从中国大陆、香港、上海等地飞往乌克兰的飞机，从北京飞往乌克兰首都基辅，基辅飞到中国北京、上海、香港，等地的飞机.热点二：21年日本奥运会上，某运动员投掷标枪时，标枪的初速度的记录资料是：平时出手角度θ=43.242°，平均出手速度大小为v=28.36m/s.问题，上述实例中，“位移”、“速度”、“力”与生活中，我们接触到的长度、面积、重量等有什么区别？如何表示上述既有大小又有方向的量？不论是奥运会的热点还是中国撤侨的热点，都是关乎中国国力的大事，在这些对生活中的热点问题的关注的动机的驱动下，学生们认识到国家强大、国立强盛，中国人民才能真正屹立在世界民族之林.在数学学习实践中，用实时热点，引发学生对数学、对生活的关注，对国家、对未来的关注.生活中，数学无处不在，学好数学不仅关系到学生的学习，更关系到未来学生的发展乃至国家的安全、稳定和发展.在积极的生活思维的渗透下，学生的数学意识得到有效地培养和调动，德育思想也在具体的数学教学活动中得到有效地渗透，将学习与个人、国家联系起来，在积极的民族自尊心和自豪感的驱动下，激发学生的爱国热情和责任意识，激励学生在具体的学习实践中，主动地融入到问题解决的过程中去.

2.4 寓教于乐，快乐体验

高中的数学学习也需要快乐元素的注入，进入高中阶段的数学学习，随着知识难度的增加，教师在教学设计中的问题分析和设计的过程中，可以复杂枯燥的学习对象以简单活泼的灵魂，让学生在轻松活泼的学习体验中，更加潜移默化地转化知识对象，主动地将知识对象纳入到自己的认知结构中，主动地对问题解决产生强烈的内在动机.在轻松愉悦，活泼动态的学习氛围中，助力学生的问题解决能力的有效培养和发展.

例如，在学习《随机事件及样本空间》时，教师以投硬币、掷骰子等游戏为切入点，引发学生对游戏结果的分析和推测.投掷硬币，可能得到的结果有两个，正面向上或背面向上.每一次投掷的结果是可预测的，也是不可预测的，因为每次得到的结果并不一定能够根据自己的预测来呈现.但是也是有一定的规律可循的.综合来看，大致得到的结果是相同的，其概率在0.5.同理，掷骰子也是一样的道理，最终掷出的是哪一面，其概率都是1/6，在游戏化的体验中，引出“全部可能的结果的集合是已知的”这个假定适合理的.得到了这个证实，再接下来，结合游戏过程来认识这些基础的知识概念.

总之，新课程背景下的高中数学教学中培养学生的解决问题能力，需要通过各种有效策略的实施，激发学生的主体性意识，提高学生在学习活动中的参与程度，学生对活动的参与程度高，学生的理解效果提升，在具体的学习实践中学生的积极性和能动性得到激发，学生对问题的应对和解决能力自然得到有效地提高.