全球化人才流动对国际合作的函数型动态效应可视化分析

程 豪,裴瑞敏

(1.中国科学技术协会 创新战略研究院,北京 100038;2.中国科学院 科技战略咨询研究院,北京 100190)

一、引 言

一直以来,人才流动与国际合作都是备受关注的研究主题。早在1963年,英国科学家大量外流到美国引起国际各界人士的广泛关注。立足全球视野,人才跨国与跨地区的流动情况是衡量国际合作的一个关键指标,也是影响国际合作的重要因素。人才的良性循环和流动能够为世界各国、各地带来巨大的经济社会效益,进一步加强国际间的合作,而人才的恶性流动和迁徙则会导致国际合作关系破裂,合作生态难以维持。加上COVID-19等突发事件的影响,全球化人才流动对国际合作效应会受到一定程度的冲击。随着时间的推移,全球化人才流动对国际合作的效应很可能会出现动态变化,而这种动态变化规律的描述和捕捉将成为颇具价值的研究问题。

然而,目前国内外专家学者在人才流动等相关领域更多关注的是人才流动影响因素、人才流动机制与路径探索等方面。Mahroum认为,人才流动在不同的职业生涯阶段表现出不同的动机[1]。陈韶光和袁伦渠就人才国际流动效应展开讨论,对人才国际流动绩效进行分析与评价[2]。陈波通过设计跨期工作搜寻模型解释了复杂的人才国际流动行为,并理论论证了移民输出国也可能会由于移民的跨期流动而获益[3]。杨芳娟以中国高端科技人才为对象,研究其跨国流动模式及影响[4]。龙梦晴和邹慧娟在梳理当前人才流动生态失衡现象的基础上,探究了人才流动协同发展的机理与路径[5]。作为国际互动的一种基本形式,国际合作工作相关研究成果的开展主要围绕在国际科学合作或国际科研合作现状分析以及合作模式探索。刘则渊围绕科学论文生产与科学合作规模之间的关系,发现科学合作最佳规模现象,并提出全面探索科学合作最佳规模现象与定律的设想[6]。刘云等根据基础学科国际科学合作的重要特征以及国际科学合作的产出数据系统,研究了国际科学合作中所出现的复杂现象与关系,并就基础学科国际科研合作的重要模式进行了讨论[7]。陈立新等就近17万条力学SCI专业期刊论文索引数据进行统计分析,研究表明国际力学科学合作中存在马太效应[8]。袭继红等以2009—2011年Web of Science中收录外科学研究文献为分析对象,研究了国际合作对论文影响力提升的作用[9]。基于已有文献不难发现,全球化人才流动对国际合作的动态效应研究较为少见。因此,这种动态效应的研究需要选择科学的方法和工具加以解决。

本文将全球化人才流动对国际合作的效应研究界定为人才流动与国际合作间的回归关系问题,与传统的线性回归关系不同的是,这里的回归关系需要考虑随着时间推移的动态变化,即人才流动与国际合作之间关系的系数需要通过光滑的函数才能刻画出全球化人才流动对国际合作的具有函数特征的动态变化规律。综上所述,本文通过选择描述具有函数特征的动态回归关系的统计学方法和模型,研究全球化人才流动对国际合作的函数型动态效应问题,并借助可视化方式展示这种函数规律,以期为政府及社会各界提供方法工具和分析思路。

二、研究设计

(一)方法选择

无论是人才流动还是国际合作,都会随着时间的推移不断产生出新数据,而仅仅关注某个时间点上的关系或规律无法实现人才流动对国际合作影响的连续动态变化。这种具有连续特征的动态变化规律需要具有函数特征的系数加以刻画。通常情况下,描述变量间关系的系数取值不会随时间的推移而发生变化,比如经典线性回归模型用于描述变量间的回归关系,但是对于本文关注的人才流动和国际合作来说,需要将系数推广为时间的函数,才可以用于捕捉人才流动对国际合作的效应变化。

系数具有函数特征的统计分析方法主要包括函数型数据分析法和变系数模型。函数型数据是将横截面数据与时间序列数据融合在一起,并使之具有函数特性的一类数据[10-11]。Ramsay和Silverman全面阐述了函数型数据的基本特征以及统计分析的思想,极大地促进了函数型数据分析方法的理论发展及其在生物医学、气象学、经济学等诸多领域的应用[12-13]。与传统的统计分析方法相比,函数型数据分析法之所以如此广泛受欢迎是因为:首先,该方法很少依赖于模型构建的假设条件,可以实现无限维空间数据的统计分析,能够利用更多的数据信息;其次,该方法中的假设函数都是可导的,因此可进行微分分析;最后,该方法将多元统计方法进一步延伸于函数型数据分析。目前,函数型数据分析主要从几个角度展开:函数型主成分分析、函数型聚类分析、函数型判别分析以及函数型回归分析,其中,函数型线性回归模型一直是函数型数据研究的重点[14-22]。

变系数模型是一种使得系数具有函数特征的方法[23]。该模型将一般线性模型的回归系数推广到某些因子的非参数函数中,保留了非参数回归的稳健性特点,且回归系数是一维变量(如空间、时间)的函数,有力克服数据的高维灾难。目前,变系数模型广泛应用于局部多维回归分析、函数数据分析、纵向数据分析、非线性时间序列分析等诸多领域,并且动态广义线性模型、可加模型、部分线性模型、单指标函数系数回归模型和可适应的变系数模型等很多常见模型均属于其特殊情形[24-27]。目前,变系数模型的研究成果主要从以下几个角度展开:统计推断、部分变系数模型与广义变系数模型、纵向数据分析、生存分析、变量选择等[28-37]。

在全球化人才流动对国际合作动态效应研究中,人才流动和国际合作均属于连续测量的数据,而人才流动对国际合作的影响或作用明确表示出以人才流动为自变量、以国际合作为因变量的回归关系,这种回归关系区别于普通线性回归,要求变量和系数均为时间的函数。而函数型数据分析从函数的角度,将连续测量的数据视为具有函数特征的动态概念[13]。需要说明的是,函数型回归模型共包括四种类型:第一,响应变量是一维随机变量,解释变量是函数;第二,响应变量是函数,解释变量是向量;第三,响应变量和解释变量都是函数;第四,函数型广义线性模型。在全球化人才流动对国际合作的函数型动态效应研究中,结合人才流动和国际合作数据特点,本文采用响应变量和解释变量都为函数的这类函数型回归分析作为研究方法,函数型回归模型表达式如下:

Y(t)=β0(t)+β1(t)×X(t)+ε(t)

其中,Y(t)表示因变量,X(t)表示自变量,β0(t)表示截距项,β1(t)表示回归系数项,ε(t)表示随机误差项。显然,上述变量与系数项均为时间t的函数。本文中,模型的因变量为国际合作,模型的自变量为人才流动,截距项和回归系数项用于揭示人才流动对国际合作的函数型动态效应规律。

(二)研究问题

第一,研究对象和时间长度的确定。全球化人才流动对国际合作的函数型动态效应研究首先需要解决研究对象的问题。在一个时间点上,研究对象存在取值不难,但在一定的时间长度内,研究对象持续存在取值不易。因此,需要确定好一定时间长度内每个时间点上均存在取值的研究对象。这里,一定时间长度要在保证一定的研究对象数量的基础上进行选择,而且一定时间长度最好尽可能地覆盖最新时刻,以确保所反映规律的实时性。

第二,人才流动变量的选择。另一个重要问题是,影响国际合作的因素众多,虽然本文从人才流动视角出发,仅考虑人才流动相关的因素,但众所周知,人才流动从方向上可简单分为人才流入和人才流出[4]。受数据获取等因素的限制,本文不考虑人才环流现象。在函数型回归模型中,国际合作为因变量,而自变量的纳入需要从人才流入、人才流出以及人才流动总体情况这三个维度加以考虑。其中,人才流动总量是人才流入和人才流出的加总。因此不建议将人才流动总量和人才流入量,或者人才流动总量和人才流出量同时纳入模型。那么,在全球化人才流动对国际合作的函数型动态效应模型中,可以仅纳入人才流动总量、人才流入量和人才流出量中的一个变量作为自变量,依次建模。然而是否可以将人才流入量和人才流出量同时作为自变量纳入模型,有待通过计算相关系数加以确定。

第三,函数型动态效应规律的描述与可视化分析。通过函数型回归分析,分别描述人才流动不同变量对国际合作的动态效应规律。在所选时间长度中,如果出现前后段不同特点的变化规律,可以考虑截取部分时间长度的数据深入挖掘人才流动对国际合作的函数型动态效应规律。考虑到函数型数据的特点,本文借助可视化工具对数据统计特征以及人才流动对国际合作的函数型动态效应规律加以展示。

三、实证分析

(一)人才流动与国际合作整体动态变化描述

本文采用Scopus数据库的部分数据,包括1981—2020年108个国家(地区)的人才流动和国际合作数据,涉及不同国家(地区)的人才流出量(varout)、人才流入量(varin)、人才流动总量(varsum)及国际合作(varco)共4个变量。其中,人才流动总量是人才流出量与人才流入量之和,国际合作采用跨国合作的文章数量来表示。本文首先通过折线图(如图1所示)展示所有国家(地区)从1981—2020年在国际合作方面的变化规律。考虑到不同国家(地区)在人才流动与国际合作方面的数据量级相差较大、国家(地区)数量较多的数据特点,图1将108个国家(地区)平均分为9组,对国际合作数据取对数,再绘制折线图。需要说明的是,图例用不同国家(地区)的代码代替国家(地区)名称。

1981—2020年,绝大多数国家(地区)在国际合作方面表现出稳定上升的特征,而且不同国家(地区)的国际合作上升趋势呈现出平行的特点,只有极个别的国家(地区)出现一定程度的波动。此外,人才流出量、流入量和流动总量也表现出与国际合作相似的规律,受篇幅所限,本文省略了人才流动方面的折线图。

为进一步研究1981—2020年各国家(地区)在国际合作、人才流入量、人才流出量、人才流动总量共四个方面的变化规律,本文先对每一年各国家(地区)在上述四个方面的数据取对数,再计算取对数后的最值、分位数和均值结果,如图2所示。其中,最大值记为max,最小值记为min,均值记为mean,第一分位数记为Q1,中位数记为median,第三分位数记为Q3。

图2共包含四个子图,从左至右分别展示了各国家(地区)在国际合作、人才流入量、人才流出量、人才流动总量的变化规律。在每个子图中,从上到下分别展示出最大值、第三分位数、均值、中位数、第一分位数和最小值共六条折线。不难看出,国际合作、人才流入量、人才流出量、人才流动总量方面在最值、分位数和均值方面表现出相似的变化规律:(1)所有折线整体上均表现出上升趋势,且国际合作比其他三个变量上升的速度更大,所有国际合作的发展形势更优于人才流动的数量;(2)所有折线表现出平行特点,即同一个子图的不同折线间保持着相对稳定的距离,说明不同国家(地区)随着年份的推移在国际合作与人口流动方面的差距没有表现出扩大或缩小的规律;(3)均值略高于中位数,且两条折线非常接近,在一定程度上说明,数据分布相对集中,离散程度相对较小;(4)与其他五条折线相比,最小值表现出较大幅度的波动性,而且这种波动性在前20年尤为明显,这种特点很可能揭示出近20年人才流动与国际合作发展规律更加稳定,为后续进行函数型动态分析提供基础。此外,本文还绘制了箱线图,考虑到箱线图中所涉及的最值、分位数等数据信息与图2所展示的内容类似,且分析规律一致,所以这里不再进行展示。

(二)人才流动对国际合作函数型动态效应

对1981—2020年所有国家(地区)的人才流出量、人才流入量、人才流动总量及国际合作共4个变量原始数据的相关系数进行计算。需要说明的是,人才流动总量为人才流出量和人才流入量之和,因此不计算人才流动总量与人才流出量之间,以及人才流动总量与人才流入量之间的相关系数。图3展示出1981—2020年所有国家(地区)国际合作与人才流入量、人才流出量、人才流动总量之间的相关系数(分别记为varco-varin、varco-varout和varco-varsum),以及人才流出量与人才流入量之间的相关系数(记为varin-varout)。

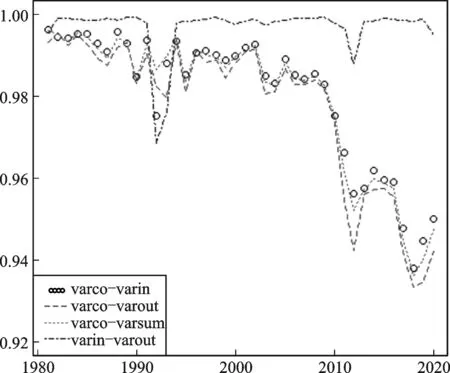
图3 1981—2020年变量间相关系数折线

由图3可知,国际合作与人才流入量、人才流出量、人才流动总量之间的相关系数随着年份的推移整体呈现出一种下降的趋势,而在2012年和2018年各有一次较大程度的“先下跌,后回升”的变化。人才流出量与人才流入量在除1992—1993年的较大程度变动外,均表现出接近1.00的高度相关水平,因此在构建人才流动对国际合作函数型动态效应模型时,人才流出量与人才流入量不可同时纳入模型中,避免出现多重共线性的问题。而人才流动总量为人才流入量与人才流出量之和,因此,人才流动总量也无法与人才流入或流出同时纳入模型。综上所述,本文以国际合作为因变量,分别以人才流入量、人才流出量、人才流动总量为自变量,构建三个人才流动对国际合作函数型动态效应模型。为方便表述,记模型1为人才流入对国际合作函数动态效应模型,模型2为人才流出对国际合作函数动态效应模型,模型3为人才流动总量对国际合作函数动态效应模型。

首先,本文基于1981—2020年共40年的原始数据,分别构建三个模型,模型形式如下:

Varco(t)=β01(t)+β11(t)×Varin(t)

(1)

Varco(t)=β02(t)+β12(t)×Varout(t)

(2)

Varco(t)=β03(t)+β13(t)×Varsum(t)

(3)

模型(1)～(3)中,Varco(t)表示国际合作的年份t的因变量函数,Varin(t)表示人才流入量的年份t的自变量函数,Varout(t)表示人才流出量的年份t的自变量函数,Varsum(t)表示人才流动总量的年份t的自变量函数。本文采用样条法估计模型中的未知参数函数β01(t),β11(t),β02(t),β12(t),β03(t)和β13(t)。这里年份t的取值范围是[1981,1982,…,2020]。

图4展示出1981—2020年人才流动对国际合作函数型动态效应曲线,该图共包括上下两层,上层从左至右分别表示截距项β01(t),β02(t)和β03(t)的函数曲线(左)及其变化曲线(右),下层从左至右分别表示系数项β11(t),β12(t)和β13(t)的函数曲线(左)及其变化曲线(右)。图例给出了对应曲线表达的因变量与自变量间的回归关系。

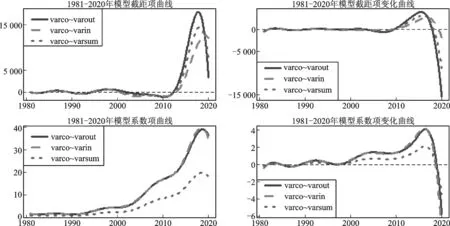
图4 1981—2020年人才流动对国际合作函数型动态效应曲线

由图4左侧两个子图可知,人才流动总量、人才流入量、人才流出量对国际合作的函数型动态效应(包括截距项和系数项)表现出一致的规律性,即截距项曲线和系数项曲线均先经过一段时间的取值较小的稳定状态,而后以较快的速度上升,最后再经历下降。但随着年份的推移,不同人才流动自变量对国际合作因变量的效应的变化幅度不同。2015年前后,人才流出量对国际合作截距项效应上升幅度最大,人才流动总量对国际合作截距项效应上升幅度次之,人才流入量低于人才流动总量和人才流出量。人才流入量和人才流出量对国际合作的系数项效应非常接近,而2000年以后人才流动总量对国际合作的系数项效应尽管保持相对快速上升的趋势,但与人才流入量和人才流出总量对国际合作的系数项效应相比,其上升的幅度差距不断增加。图4右侧的两个子图表示截距项和系数项的变化曲线,即左侧曲线对应的变化曲线,在2000年以前,截距项和系数项的变化曲线基本在0水平线附近波动。2015年以后,截距项变化曲线和系数项变化曲线出现明显的迅速下降趋势,2020年达到最低。截距项和系数项的变化曲线表明人才流入量、人才流出量、人才流动总量对国际合作的函数型动态效应的变化速度表现出先以相对稳定的速度变化,再经过大幅度上升的加速变化,而后出现较为剧烈的大幅度下降的反向加速变化(取值为负)。

2001年以后,截距项、系数项曲线及其变化曲线均表现出较大幅度的变化特点。为此,本文将数据限制在2001—2020年共20年的原始数据,重新构建模型(1)～(3),在排除1981—2000年数据干扰的前提下,探索近20年的函数型动态效应规律。与图4结构相同,图5展示出2001—2020年人才流动对国际合作函数型动态效应曲线。该图共包括上下两层,上层从左至右分别表示截距项β01(t),β02(t)和β03(t)的函数曲线(左)及其变化曲线(右),下层从左至右分别表示系数项β11(t),β12(t)和β13(t)的函数曲线(左)及其变化曲线(右)。这里,年份t的取值范围是[2001,2002,…,2020]。图例给出了对应曲线表达的因变量与自变量间的回归关系。

图5 2001—2020年人才流动对国际合作函数型动态效应曲线

由图5左上方的子图可知,2010年以前,人才流动总量、人才流入量、人才流出量对国际合作的截距项的函数型动态效应非常接近,在0附近波动。而在2010—2018年,呈现出较为明显的上升趋势,2018年以后人才流出量和人才流动总量对国际合作的截距项的函数型动态效应呈现先增长后下降的趋势,人才流入量对国际合作的截距项的函数型动态效应在先增长后平稳下降后再次出现上升的趋势。人才流动总量、人才流入量、人才流出量对国际合作的截距项函数型动态效应的变化曲线在2010年前保持在0水平附近波动而后出现上升趋势。2016年以后,人才流入量和人才流动总量对应的截距项变化曲线在下降后出现上升,而人才流出量对应的截距项变化曲线保持持续下降。由图5下方的两个子图可以看出,人才流入量、人才流出量对国际合作的系数项的函数型动态效应曲线及变化曲线非常接近,效应曲线呈现阶段性的上升趋势,而效应变化曲线表现出一定的周期性且没有明显的上升趋势。人才流动总量对国际合作的系数项的函数型动态效应曲线及变化曲线的规律与人才流入量、人才流出量对应的曲线规律类似,区别在于变化幅度更为平缓。

四、总结与展望

(一)主要结论

众所周知,全球化为世界的发展带来重要影响。全球化人才流动正以波涛汹涌之势,在推动经济全球化、科技国际化不断深化的同时,影响着国际合作的发展。人才流动的方向(比如,流入、流出)以及人才流动的数量直接促进或阻碍一个国家的国际竞争力,对于国际关系的维护和发展发挥着决定性的作用。在瞬息万变的国际形势中,这种决定性的作用又会随着时间的推移不断发生变化。因此,本文以函数型回归为基础模型,充分考虑人才流动的方向,构建三个全球化人才流动对国际合作函数型动态效应模型,旨在研究全球化人才流动对国际合作的具有函数特征的动态变化规律,并以可视化方式展示这种函数规律,以期为政府及社会各界提供方法工具和分析思路。

通过统计描述不难发现,1981—2020年,绝大多数国家(地区)在人才流出量、流入量、流动总量以及国际合作方面表现出稳定上升的特征,而且不同国家(地区)的国际合作上升趋势呈现出平行的特点,只有极个别的国家(地区)出现一定程度的波动。通过依次计算所有国家(地区)在国际合作、人才流入量、人才流出量和人才流动总量的最值、分位数和均值,本文发现四个变量的所有统计特征均表现出不同程度的上升趋势,而不同国家(地区)随着年份的推移在国际合作与人口流动方面的差距没有表现出扩大或缩小的规律。其中,最小值在前20年和后20年表现出不同的差异。基于上述分析,结合不同人才流动变量间的相关系数,本文以1981—2020年和2001—2020年为时间段各构建三个全球化人才流动对国际合作函数型动态效应模型,用于探索人才流动对国际合作的函数型动态效应规律,研究表明:

(1)选择1981—2020年为时间段构建模型发现,不同人才流动变量对国际合作的函数型动态效应(包括截距项和系数项及其变化)均先经过一段时间取值较小的稳定状态,而后以较快的速度突然上升,最后再经历下降。2015年前后,人才流出量对国际合作截距项效应上升幅度最大,人才流动总量对国际合作截距项效应上升幅度次之,人才流入量低于人才流动总量和人才流出量。人才流入量和人才流出量对国际合作的系数项效应非常接近,而2000年以后人才流动总量对国际合作的系数项效应尽管保持相对快速上升的趋势,但与人才流入量和人才流出总量相比,其上升的幅度差距不断增加。

(2)选择2001—2020年为时间段构建模型发现,不同人才流动变量对国际合作的截距项的函数型动态效应在开始非常接近。直到2010年,呈现出较为明显的上升趋势,2018年以后人才流出量和人才流动总量对国际合作的截距项的函数型动态效应呈现先增长后下降的趋势,而人才流入量对国际合作的截距项的函数型动态效应在先增长后平稳下降后再次出现上升的趋势。2016年以后,人才流入量和人才流动总量对应的截距项变化曲线在下降后出现上升,而人才流出量对应的截距项变化曲线保持持续下降。人才流入(出)量对国际合作的系数项的函数型动态效应曲线及变化曲线几乎全程重合。其中,效应曲线呈现阶段性的上升趋势,而效应变化曲线表现出一定的周期性且没有明显的上升趋势。

综上所述,在国际竞争日益激烈、全球化挑战日趋显著、新冠肺炎疫情突如其来的背景下,充分发挥人才流动的力量,推动国际合作健康有序的发展,已成为全世界共同关注的重要话题。本文借助科学的建模方法和可视化工具,完成全球化人才流动对国际合作函数型动态效应规律的分析,并提出相关政策建议,以期为全球化人才流动治理与国际合作等相关领域建言献策,为政府及社会各界提供参考。

(二)政策建议

基于全球化人才流动对国际合作函数型动态效应的研究结果,针对近些年来人才流动变量对国际合作效应的变化规律,本文提出如下政策建议:

(1)深耕全球人才流动治理。人才国际流动是全球化发展的重要特征之一。驻足国际视野,百年变局和世纪疫情交织叠加,国际格局发生深刻调整,全球人才和科技竞争更加激烈,应科学制定国际人才管理和移民规则,通过互惠共赢的国际合作机会,引导人才流动朝着良性健康的方向发展。在全球化人才流动治理中,要注重与全球经济治理、全球安全治理等相关工作同时推进,不断挖掘全球人才流动治理尚待解决和可能存在的难题。

(2)深化竞争领域国际合作关系。不断强化金砖国家国际竞争大会等重要合作平台建设、深化医药食品、数字经济等重点领域的合作交流,构建起全方位、复合型的互联互通国际合作关系,开创公平竞争与疫后经济增长、数字经济时代的竞争政策发展等竞争领域共同发展的新前景,持续推进全方位、多层次、宽领域的国际交流与合作。

(3)合力人才流动与国际合作稳中求进的发展态势。当前国际环境错综复杂,新冠肺炎疫情影响广泛深远,世纪经济陷入低迷期,不稳定性明显增加,人才流动与国际合作的发展能否保持稳定的发展状态,并在复杂环境中激流勇进,需要世界各国守望相助,共克时艰,坚持走团结合作、互联互通、共同发展之路,为全球抗疫合作和经济复苏作出重要贡献。

(4)以卓越科技创新能力夯实国际合作基础。在实施国际科技合作战略中,独立自主办大事、办难事、办急事,打造优势领域“长板”,提升科技自主创新能力,夯实国际合作基础。多措并举推进国际科技交流合作,深化科技体制改革,把蕴藏在中国人才队伍中的巨大创新潜能有效释放出来。

(5)构建良好人才政策生态引导国际人才流动方向。建立健全人才政策体系,营造良好生态,发起吸引和集聚全球高水平人才的大科学计划。深入实施新时代人才强国战略,吸引人才、留住人才,加快建设世界重要人才中心和创新高地,为社会主义现代化建设打好人才基础。

(三)未来展望

下一步将继续围绕全球范围内人才流动对国际合作效应主题,并在此基础上,融入更多影响人才流动、国际合作的因素(比如,经济水平、政治制度、文化氛围等方面),以及体现人才流动效应(比如,科研产出、合作规模等方面)的指标,进一步丰富全球化人才流动对国际合作效应模型的构成要素。伴随模型构成复杂度的增加以及考虑要素个数的增多,全球范围内人才流动对国际合作效应研究将有可能面临计算复杂度高以及维数灾难等诸多问题,这对函数型数据分析方法运算效率提升及其在高维数据中的变量选择都带来不小挑战。本文所采用的函数型回归分析仍基于经典线性回归模型方法。放眼全球,不同国家和地区的人才流动状况不同,其对国际合作的效应也存在多元化的差异。在这种情况下,需要借助分位回归的思想,捕捉不同分位水平下自变量对因变量的函数变化规律。因此,函数型分位回归模型的深入开发及其在全球范围内人才流动对国际合作效应的应用将颇具意义。