利用极限的保号性解决与极值点有关的函数问题

邓启龙

(广东省中山纪念中学 528454)

与极值点有关的函数问题,近年来频频出现在高考试题中,例如2018年北京卷理科数学第18题和2018年全国Ⅲ卷理科数学第21题.特别是2018年全国Ⅲ卷理科数学第21题,该题题目简洁,但难度很大,官方的参考答案思维巧妙,逻辑严密,很难想到.本文通过深入探究,利用极限的保号性解决此类与极值点有关的函数问题.

首先给出本文要用到的几个引理.

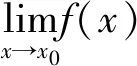
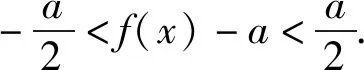
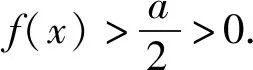
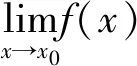
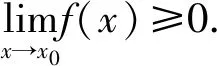
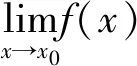
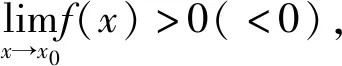
引理1,2,3是由函数极限的保号性得到的结论.接下来利用以上引理来解决几个典型的与极值有关的函数问题.

例1(2018年北京卷理18第(2)问)设函数f(x)=[ax2-(4a+1)x+4a+3]ex.若f(x)在x=2处取得极小值,求a的取值范围.

解法1f′(x)=[ax2-(2a+1)x+2]ex

=(ax-1)(x-2)ex.

由f(x)在x=2处取得极小值得∃δ>0,当x∈(2-δ,2)时,f′(x)<0,当x∈(2,2+δ)时,f′(x)>0.

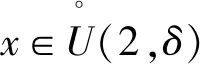
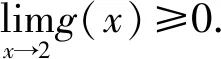
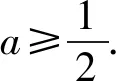
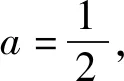
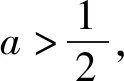
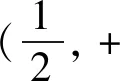
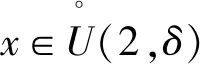
[ax2-(4a+1)x+4a+3]ex≥e2.

得(x-2)2exa+(3-x)ex-e2≥0.

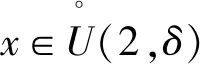
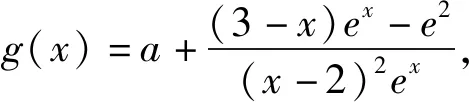
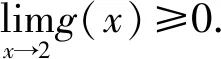
由洛必达法则,得

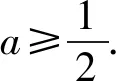
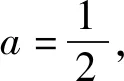
于是f(x)在(-∞,+∞)上单调递增,没有极值点,不符合题意.

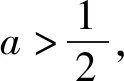
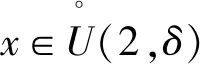
即f(x)>f(2).

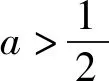
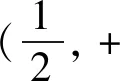
例2(2018年全国Ⅲ卷理21第(2)问)已知函数f(x)=(2+x+ax2)ln(1+x)-2x.若x=0是f(x)的极大值点,求a.

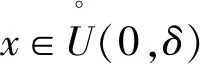
即(2+x+ax2)ln(1+x)-2x≤0.

得x2ln(1+x)a+(2+x)ln(1+x)-2x≤0.

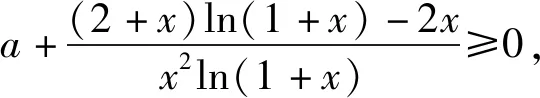
当x∈(0,δ)时,

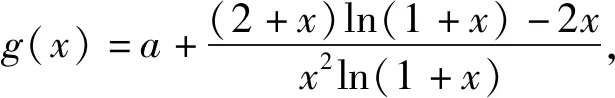
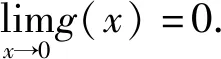
由洛必达法则,得

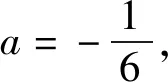
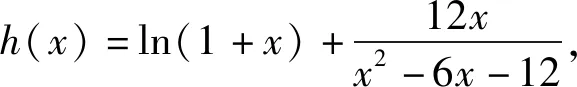
当x∈(-1,0)时,h′(x)>0,当x∈(0,1)时,h′(x)<0.于是h(x)在(-1,0)上单调递增,在(0,1)上单调递减.

所以当x∈(-1,1)时,h(x)≤h(0)=0.

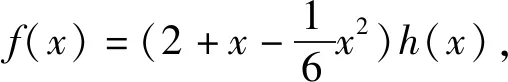
所以当x∈(-1,1)时,f(x)≤0.

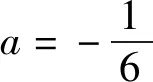
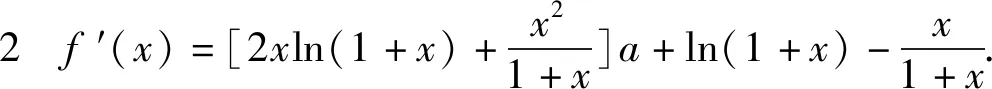
由x=0是f(x)的极大值点得∃δ>0,当x∈(-δ,0)时,f′(x)>0,当x∈(0,δ)时,f′(x)<0.

易得∀x∈(-1,0)∪(0,+∞)时,

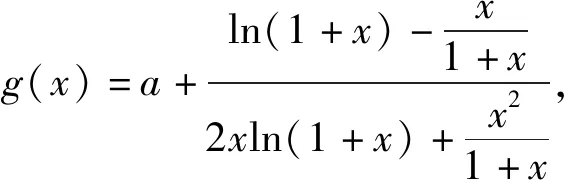
则∃δ>0,当x∈(-δ,0)时,g(x)>0,当x∈(0,δ)时,g(x)<0.

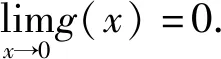
由洛必达法则，得

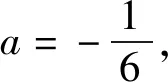
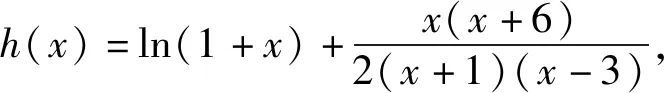
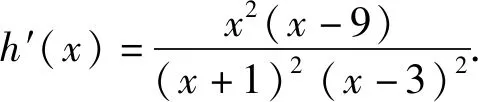
当x∈(-1,1)时,h′(x)≤0,于是h(x)在(-1,1)上单调递减.

又h(0)=0,所以当x∈(-1,0)时,h(x)>0,当x∈(0,1)时,h(x)<0.

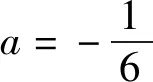
解法3f(x)=(2+x+ax2)ln(1+x)-2x

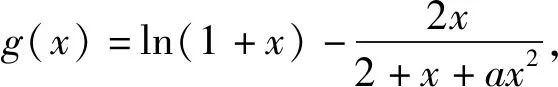
由x=0是f(x)的极大值点易得x=0也是g(x)的极大值点,于是∃δ>0,当x∈(-δ,0)时,g′(x)>0,当x∈(0,δ)时,g′(x)<0.

不妨设0<δ<1,则当x∈(-δ,0)时,a2x2+4ax+6a+1>0,当x∈(0,δ)时,a2x2+4ax+6a+1<0.

由引理3，得

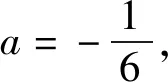
当x∈(-1,0)时,g′(x)>0,当x∈(0,1)时,g′(x)<0.

于是g(x)在(-1,0)上单调递增,在(0,1)上单调递减.

所以当x∈(-1,1)时,g(x)≤g(0)=0.

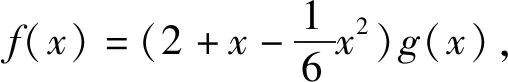
通过以上例题可以发现,解决此类与极值点有关的函数问题的关键,是先将已知条件转化为极值点x0的某去心邻域上f(x)或f′(x)的不等式,然后通过类似分离参数的方法构造包含参数的函数,利用引理2或引理3得到参数的取值范围,并说明取值范围的充分性.