第52届国际物理奥林匹克竞赛实验试题1的介绍与解答

李文华,王 槿,惠王伟,刘丽飒,宋 峰,孔勇发

(南开大学 a.物理科学学院; b.基础物理国家级实验教学示范中心，天津 300071)

2022年7月10-17日，南开大学物理科学学院率领中国代表队参加了由瑞士主办的第52届国际物理奥林匹克竞赛(International Physics Olympiad，IPhO).参赛的5名中学生全部获得金牌，并取得团体第一、总分第一、实验总分第一和理论总分第一的优异成绩.比赛采取线上方式，其中实验考试首次采用全线上远程虚拟考试.实验试题有2道，分别为行星(Planet)和柱状二极管(Cylindrical diode)[1].实验试题总分20分，试题1计12分，试题2计8分.本文介绍了实验试题1的命题并给出解答，并对题目结构及学生的答题情况做简要分析.

1 试 题

你发现自己在陌生的行星上，却不知道如何到达的.要做的第一件事是更多地了解你所在的这颗行星.你还记得伽利略是如何用落球做实验的，并受此启发建造了高度为H=2 000 m的理想竖直的塔(图1).有了这座塔，便可以从塔上任意高度h(球的底部到地面的高度)抛球.由于受所能获得的材料限制，因此只能抛下半径5 cm≤r≤50 cm，密度0.1 g/cm3≤ρ≤10 g/cm3的球.

图1 艺术家对本题的夸张描绘

任何时候都从静止开始释放球，并能够测量球下落到地面所经历的时间t，以及球的落点位置距其抛点间的水平距离s.

在开始实验前，对这颗行星做了以下观察:

1)根据恒星的运动，发现自己正处于该行星赤道的某处.

2)这颗行星有大气层，但大气密度小,可以忽略大气浮力.

3)地表温度为T0=20 ℃.

4)似乎有一股沿着赤道吹的风，在整个塔的高度上风速均匀，忽略塔对风速的影响.

1.1 仿真软件介绍

在已知球抛下的高度h、球半径r和密度ρ时，命令行程序模拟球的下落时间t和球落点位置偏离塔基的距离s的测量.在相应的提示后通过键盘可输入对应参量的值，并通过按回车键(Enter键)进行确认.

开始操作前，在界面提示时输入以下授权密码:12345678.888.如果输入密码错误，程序将进入测试模式，此时需要重启程序.

软件程序单个模拟周期的典型输出界面如图2所示.

图2 软件程序运行的典型界面

首先输入以m为单位的高度h(0～2 000之间的数),然后输入以cm为单位的球半径r(5～50之间的数)，最后输入以g/cm3为单位的球密度ρ(0.1～10.0之间的数).每次输入都要用回车键(Enter)确认.程序将输出以s为单位的t和以m为单位的s.

然后程序进行循环，重复上述过程.输入超出实验范围的值，程序界面会给出报错提示“Value Out Of Bounds”,然后返回到回答错误的提示界面.

输入的高度h四舍五入到1 m，r四舍五入到1 cm，ρ四舍五入到0.01 g/cm3(尝试输入更精确的数是毫无意义的).

实验结果有随机误差，以模拟实际实验操作中的有限精度.参赛选手可以通过观察输出数值的波动得到误差的大小.

任何时候需要退出程序，可按Ctrl+C键.

1.2 常量列表及有用的关系式

1)引力常量G=6.67×10-11m3/(kg·s2).

2)理想气体常量R=8.314 J/(mol·K).

3)0 ℃=273.15 K.

4)横截面积为A、速度为v的球在密度为ρa的大气中受到的大气阻力为

Fd=0.24Aρav2.

(1)

5)绝热大气的密度分布为

(2)

式中，γ为绝热系数，μ为大气的摩尔质量，g为自由落体加速度，h为距离地面的高度.此密度分布到大气顶部(该处温度T=0 K)均适用.

1.3 试题

1.3.1 A部分：行星的属性(3分)

A.1 做适合的测量，并在答题卡中给定区域画出合适的图，确定该行星上的自由落体加速度g.给出结果的不确定度分析.(2.0分)

A.2 在行星上，从塔出发沿赤道向远方行走，发现你能看到塔的最大距离为L=230 km(你与塔顶的直线距离).该星球的半径Rp是多少?可假设你的高度远小于塔的高度.(0.5分)

A.3 估测该行星质量M，并给出结果的不确定度分析.哪一物理因素对你估算结果的准确性影响最大?在答题卡中勾选此物理因素(表1).(0.5分)

表1 答题卡上所列出的影响因素

1.3.2 B部分:大气的属性(6.5分)

B.1 做适合的测量，并在答题卡相应区域绘制适当的图，确定行星表面的风速u.给出结果的不确定度分析.(2.0分)

B.2 通过实验得到额外的数据，或者重新使用以前的数据，并在答题卡相应区域绘制适当的图，确定行星表面的大气密度ρa0.给出结果的不确定度分析.(1.0分)

B.3 假设大气是绝热的，绝热系数γ=1.4，做适合的测量，在答题卡相应区域画出合适的图，确定大气层的厚度H0.给出结果的不确定度分析.(3.0分)

B.4 计算大气的摩尔质量μ和塔底部的气压p0.给出结果的不确定度分析.(0.5分)

1.3.3 C部分：1 d的时长(2.5分)

C.1 做适合的测量，在答题卡相应区域画出合适的图，确定该行星上1 d的时长Tp.给出结果的不确定度分析.

2 试题解答

2.1 A部分：行星的属性

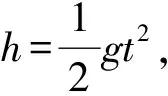
设置r=50 cm，ρ=10 g/cm3，实验数据如表2所示，做t2-h关系图如图3所示.

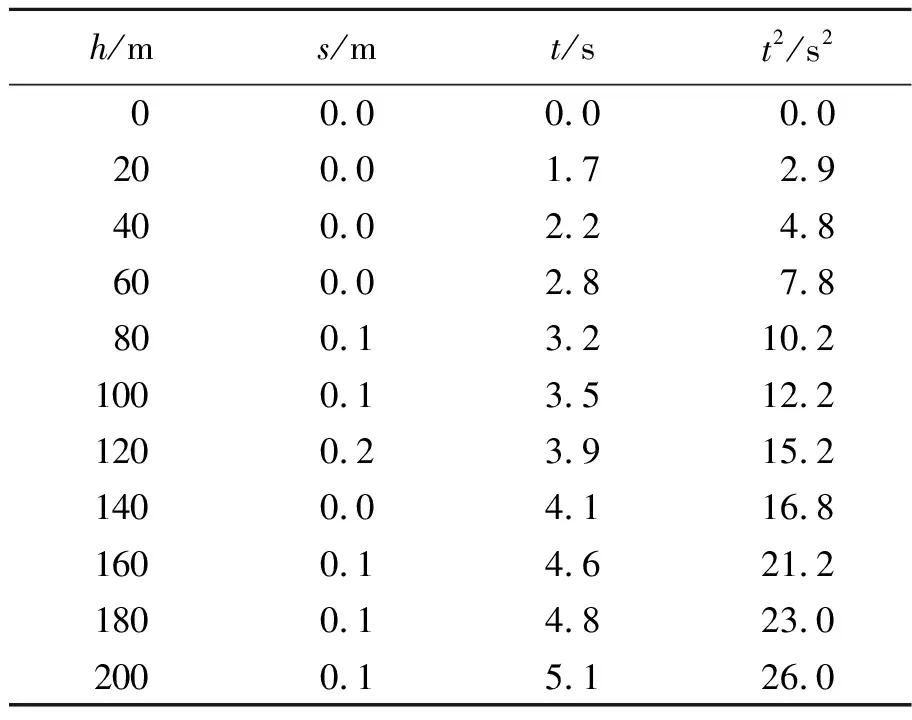
表2 不同高度释放大而重的球的落地时间

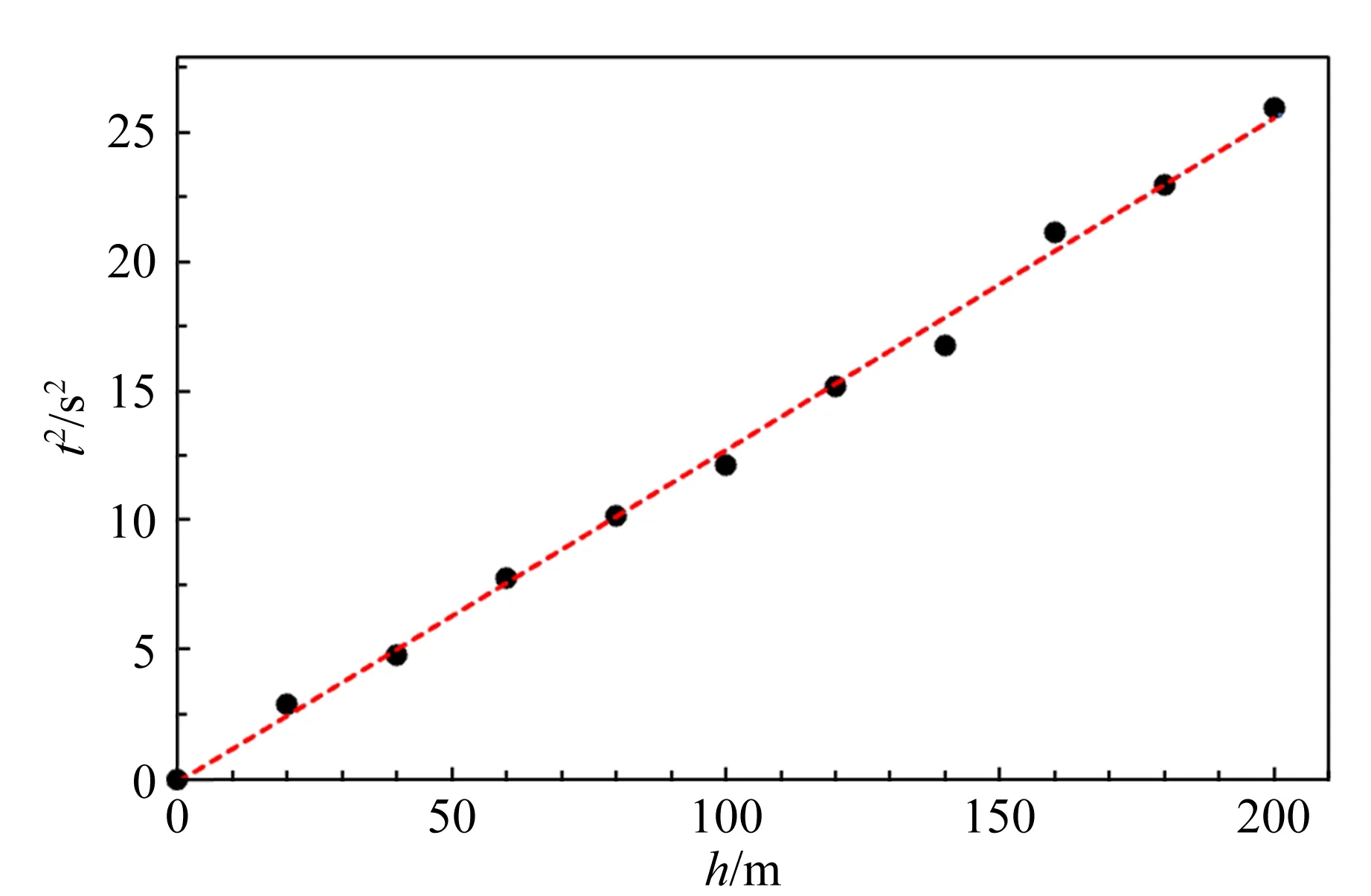
图3 t2-h关系曲线

A.2题中，在沿赤道远离塔的方向，最远可看到塔尖的距离L=230 km，可以构画出图4所示的几何关系，再利用勾股定理，可得

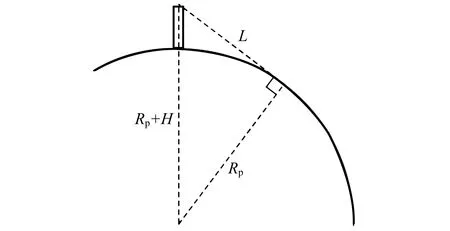
图4 远处望向塔尖的距离关系

得到行星半径为

A.3题可根据行星表面物体所受万有引力约等于重力的关系来估算行星的质量.此题建立在A.1中已求出重力加速度g和A.2中已求出行星半径Rp的基础上，得到行星的质量为

由误差传递可得到行星质量的不确定度为

在此计算中，主要用到星体的重力加速度g和半径Rp，5个选项中，只有第4项星体的自转产生的离心力对自由落体模型中的重力加速度造成影响，对行星质量估算造成的影响最大.

2.2 B部分：大气属性

2.2.1 B.1：求解风速

此部分需要求解风速的大小,因此不能再忽略大气的作用.而由式(1)可得，大气阻力(或风速)与物体的受风面积A和速度v2成正比关系，此时需通过设置落球的大小和密度，使其所受重力与大气阻力相当，即考虑利用小而轻的球从塔的不同高度落下的情况.在大气阻力和重力共同作用下，根据式(1)，球在下落初期做变加速运动，一定时间后达到恒定速度而匀速运动，此时水平方向速度即是风速.

设置r=5 cm，ρ=0.1 g/cm3，得到表3所示数据.

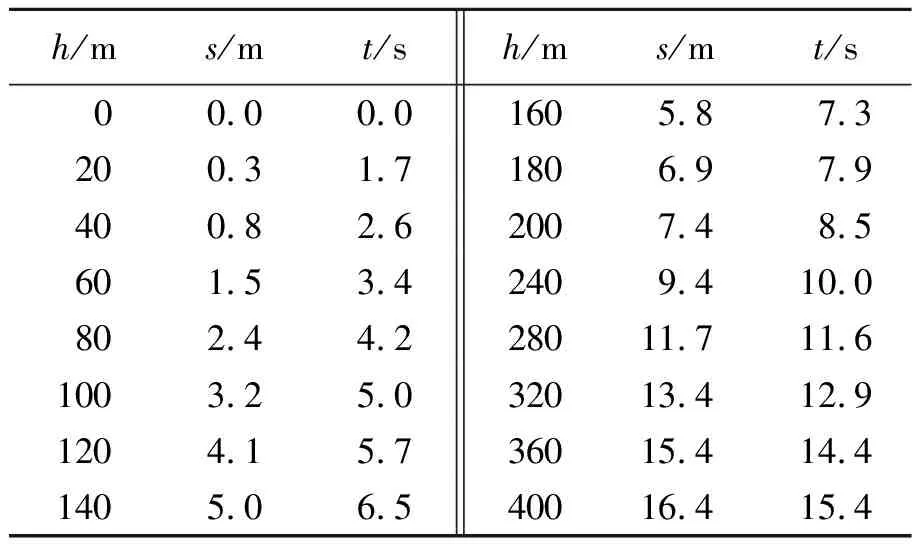
表3 不同高度轻球下落时间和水平位移的测量数据

根据表3中的数据做小轻球落地的水平位移s与落地时间t的关系曲线，如图5所示.若将小球达到恒定速度前的位移表示为s0，则总位移可表示为

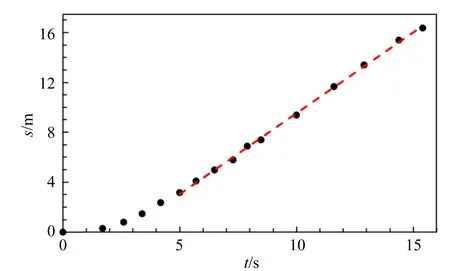
图5 水平位移s与落地时间t的关系曲线

s=s0+u(t-t0)

.

(3)

从图5中可以看到，数据在t=5.0 s左右为速度变化的拐点，对拐点之后的数据进行线性拟合，得到斜率即为风速u=1.31 m/s，不确定度Δu=0.04 m/s.

2.2.2 B.2：地表大气的密度

相比于B.1部分，小轻球在竖直方向存在：

h=h0+vt0(t-t0),

(4)

利用B.1部分的实验数据，做h与t的变化曲线如图6所示，对变化恒定部分进行线性拟合,得到速度vt0=27 m/s，不确定度Δvt0=2 m/s.

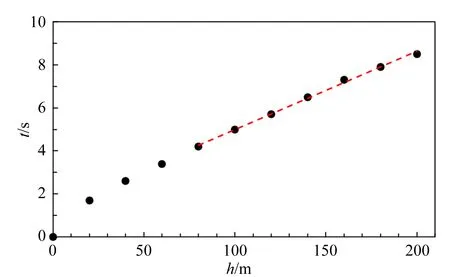
图6 行星表面小轻球落地时间随释放高度的变化

小球达到恒定速度时满足

(5)

(6)

此时，大气密度为

不确定度为

2.2.3 B.3：大气层的厚度

由式(2)可知，当大气的绝热系数γ=1.4时，可以得到

(7)

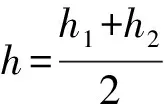
(8)

此时采集到的实验数据如表4所示，进一步处理可以得到表5的分布结果.

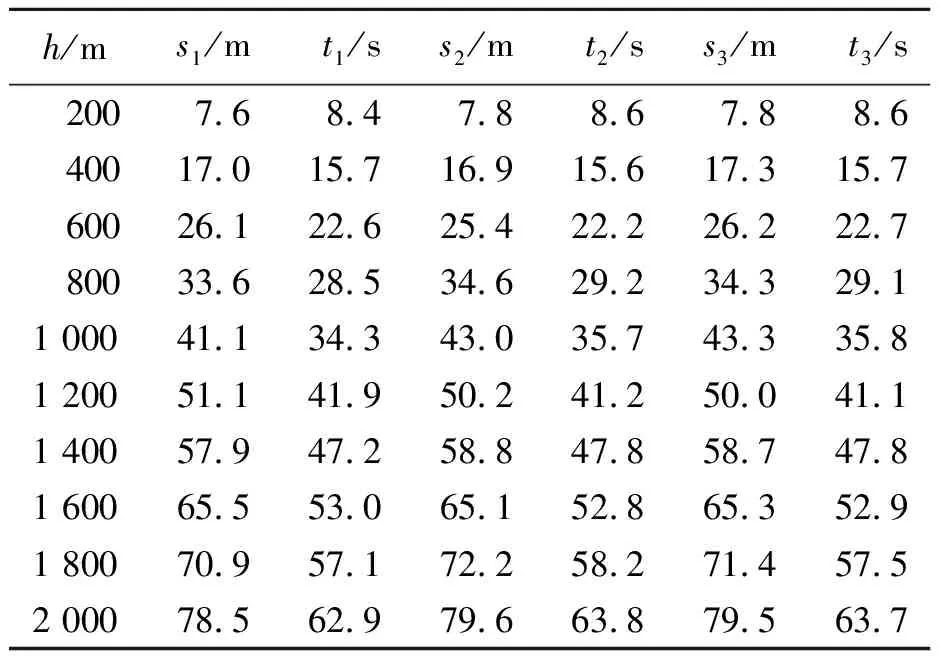
表4 在不同高度释放小轻球，等间隔落下3次的实验数据

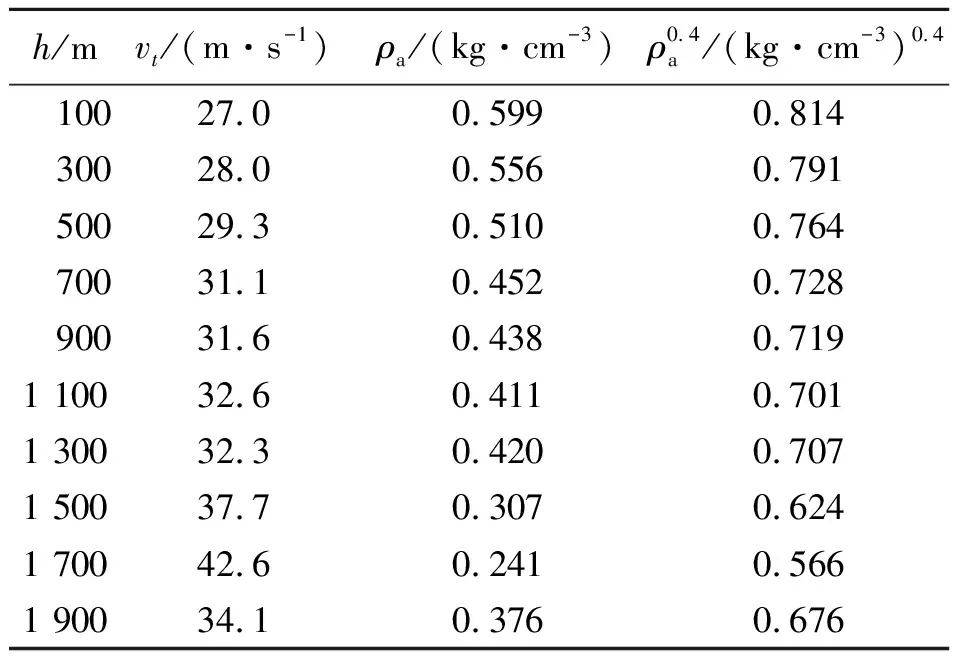
表5 不同高度的大气密度值分布

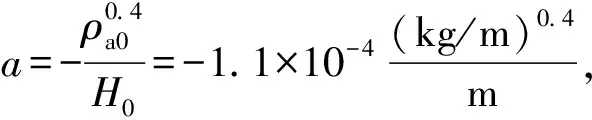
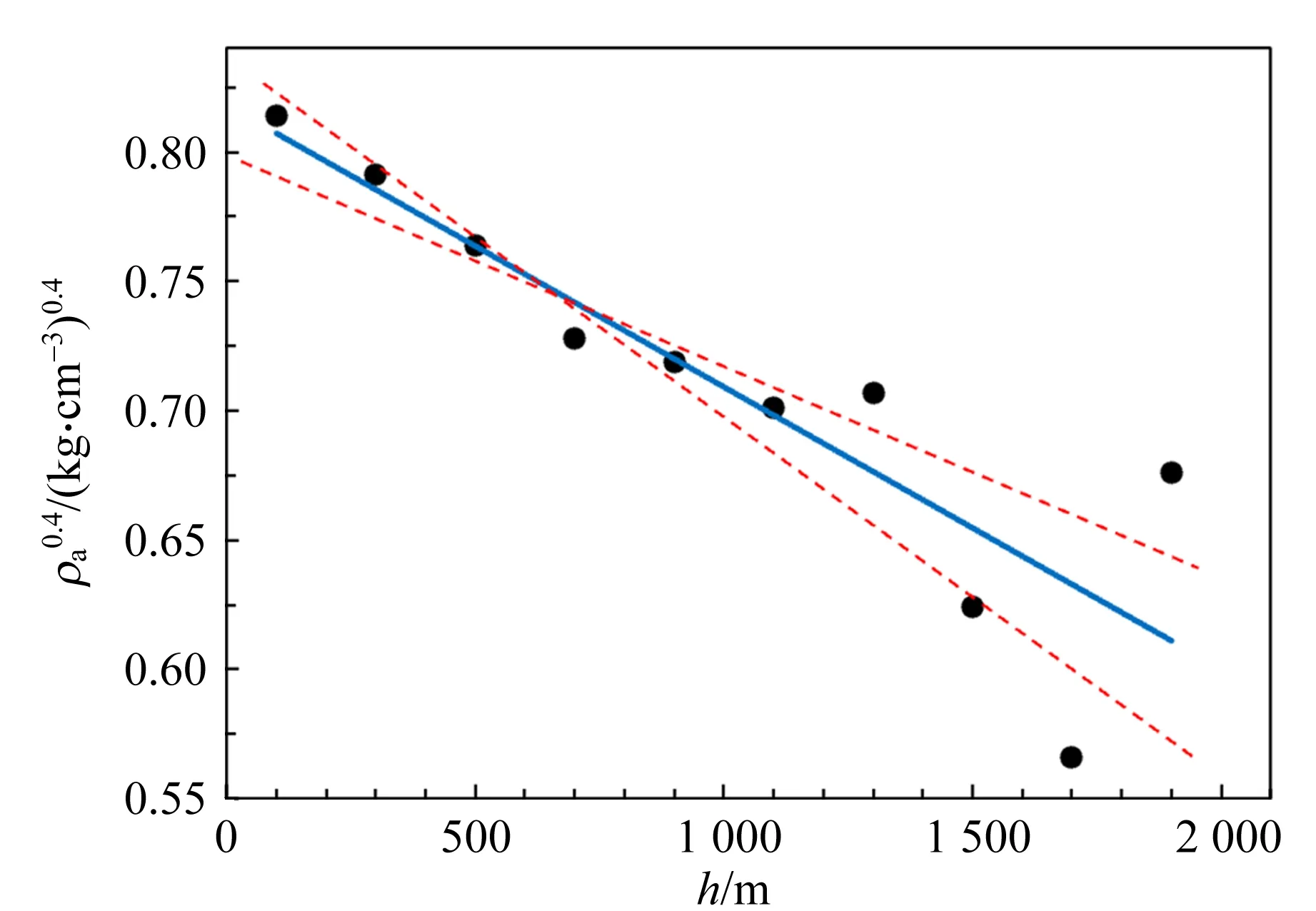
图7 大气密度随高度的变化

2.2.4 B.4：大气的摩尔质量和塔底的气压

由式(2)可以得到：

则大气的摩尔质量为

不确定度为

根据理想气体定律，塔底的气压为

不确定度为

2.3 C部分：1 d的时长

行星的1 d时长等于其自转周期，需要考虑行星的自转运动.根据题目所给信息可以得到，题目中的行星为类地行星，类地行星的自转周期主要受到其所在星系的恒星、自身卫星以及由星体间的万有引力造成的潮汐力的影响[2].答案给出的一种思路为通过求解行星的自转角速度ω来得到其自转周期.

由星体自转引起的离心力和科里奥利力会影响落体小球的运动轨迹.由于塔的高度H远小于行星半径Rp，离心力几乎与重力作用重合.科里奥利力作用于小球上，使其产生加速度为

acor=-2ω×v,

(9)

此加速度方向垂直于小球的速度方向和行星的自转轴方向，且沿赤道方向随着下落速度线性增大.则落体小球在水平方向上的加速度可以表示为

ax=2ωvy+adrag.

(10)

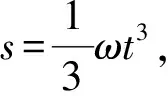
(11)

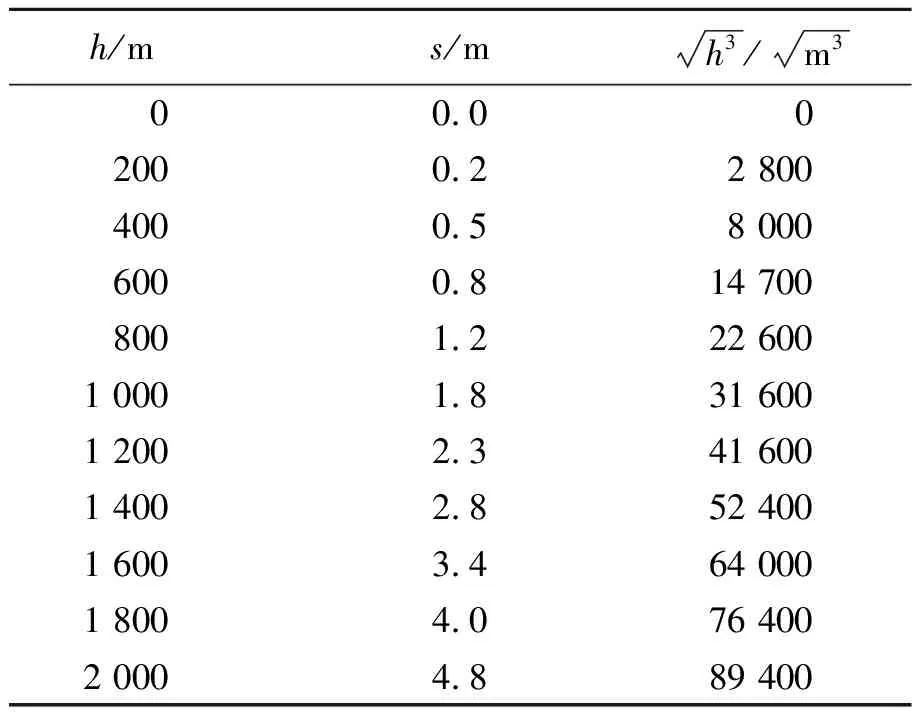
表6 科里奥利力影响下球下落高度与水平位移数据

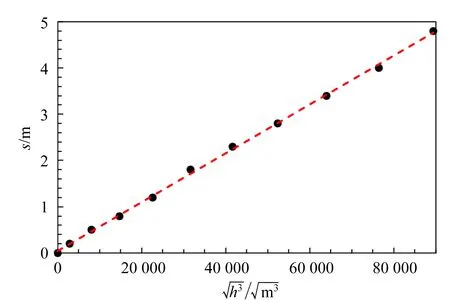
图8 科里奥利力作用下落球的水平位移随下落高度的变化

拟合得到直线的斜率为

不确定度为Δk=0.11×10-5m-1/2.行星自转周期即1 d的时长为

不确定度为

3 分析讨论

3.1 题目分析

实验试题1考查内容的物理知识背景为力学中较为经典的自由落体和万有引力定律，相对难度较低.虚拟软件程序没有采用可视化的场景界面，而是通过黑盒子界面进行物理模型推演和计算.题目的难点在于物理模型的构建，即如何选择合理的实验参量以达到理论近似的实验条件.比如风速恒定的情况下，在A.1和C.1部分，需要构造忽略大气阻力的实验条件，选择大而重的球；而在B.1～B.3部分，需要选择小而轻的球，构造受大气阻力影响较大的实验条件.实验过程中需要采集比较多的数据,通过作图法得到相应的物理量，并估算不确定度，对大部分参赛选手来说比较费时且需要细心设计.

A部分是解决后续题目的前提，如图9所示，A.1问求得的自由落体加速度g在A.3，B.2以及C.1问中均被用到；B.2在求得地表大气密度后，才能在B.3中用于求解大气厚度H0，而求得H0后，才能在B.4中继续求解得到大气摩尔质量μ和塔底气压p0.这使得题目之间有较大的连续性，如果前面题目数据误差较大，会对后续题目的解答造成影响.这也可从图9中所有获奖选手的各题平均得分率的变化趋势中看出，B.2～B.4的得分率都很低.除了自由落体和万有引力定律，试题还考查了科里奥利力.科里奥利力的知识点并未在题设中给出，而是在答题卡的A.3问中的题目选项中简单介绍.大部分选手对此物理概念了解不深，导致C.1总体得分较低.

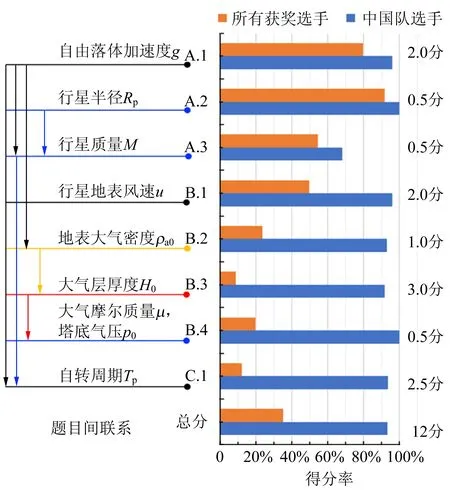
图9 试题1中各题目的联系及所有获奖选手与中国队选手各题平均得分率的对比

3.2 答题情况分析

所有获奖选手(优秀奖以上)约占总参赛人数(368人)的82%.其总分的平均得分率人数占比分布如图10所示，得分率在60%以上有23人，约占总人数的6.25%.中国队选手的总得分率均在90%以上，从图9中可以看到，中国队选手只有在A.3问上得分率较低，为68%.此问中大部分中国队选手选错了影响因素而失掉0.2分，其他小题平均得分率均在90%以上.

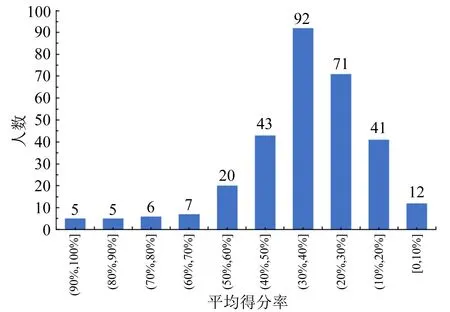
图10 试题1总分得分率区间的人数占比

4 结束语

本届国际物理奥林匹克竞赛实验试题首次采用线上虚拟实验的形式，一方面弱化了对选手实验动手能力的考查，另一方面加大了对选手实验设计思维和数据处理能力的考查.本届物理奥赛的虚拟实验模式对基础物理实验教学有一定的借鉴作用.

致谢：感谢南开大学本科生李建勋和郭丰在试卷翻译过程中的协助.感谢参与本次奥赛培训、选拔与远程考试的各位老师！感谢中国科学技术协会、中国物理学会、天津市物理学会等单位和部门对赛事的支持！