基于液晶空间光调制器的激光束散角控制技术

王姝懿，刘智，林鹏，刘树通，刘艺

（1.长春理工大学 光电工程学院，吉林 长春 130022；2.长春理工大学 空间光电技术国家地方联合工程研究中心，吉林 长春 130022；3.长春理工大学 电子信息工程学院，吉林 长春 130022）

1 引言

在以机载航空动平台为背景的激光通信系统中，随着传输距离的增大和大气湍流等信道环境的影响［1］，激光在空间传输过程中产生到达角起伏、光束扩展等现象，导致通信系统性能显著降低。为了抑制大气湍流信道环境对光束传输特性的影响［2］，使激光通信系统中的光束参数能够根据大气信道的变化进行自适应动态调整是一种可行且有效的方法。

2018年，Vuong V.Mai等人研究了两种自适应波束控制技术，其一是在发射机处调整波束发散角以最大化链路可用性，其二是在保持目标链路可用性的同时最小化发射机功率。在发射机和接收机之间对准误差的广义二维高斯分布的影响下，提供了关于链路可用性和最佳光束发散角的封闭式表达式，降低了性能优化的计算复杂度。它们可用于降低自适应波束控制所需的功耗和促进控制技术的快速运行。结果表明，自适应波束控制技术可以提高各种场景下的系统性能［3］。2019年，Vuong V.Mai等人又提出了一种快速、计算量小的自适应光束控制技术。该技术采用非机械变焦透镜，在发射端和接收端不经迭代调整光束大小，同时减小光束到达角起伏和指向误差的不利影响。研究表明，在到达角起伏和指向误差的较宽范围内，使用自适应波束控制技术的机载自由空间激光通信系统优于具有固定波束大小的系统［4］。

激光束散角作为激光光束的基本参数，对其进行动态实时控制具有重要意义。2014年，韩宽宽等人根据高斯激光束通过薄透镜的变换规律，设计了一种激光发散角在一定范围内连续变化的光学系统，能够实现远场发散角在1～200 mrad区间内连续改变［5］。2018年，张栋等人提出了一种新型的激光协同靶设计方法，该方法采用正、负透镜和锥棱镜相结合的方式，可以精确控制反射光束的发散角，且可以确保反射光束的原始返回［6］。上述传统控制束散角的方法大多数是采用机械变倍组实现对束散角的控制，通常需要使用多个已知焦距的透镜，通过不断改变透镜之间的距离实现束散角的控制，操作比较繁琐，其体积重量也无法有效降低，且动态调控效果并不理想。

近年来，液晶光学技术迅速发展。LC-SLM作为液晶光学发展的一部分，起始于20世纪70年代，它作为一种主动光学元件，能够在外加驱动信号的作用下灵活的对入射光束调制［7-8］。由于LC-SLM的灵活便捷性，它被广泛应用于液晶显示、激光整形、激光通信等各领域。随着LC-SLM技术的不断发展，国内外学者在LC-SLM对光波的调制方面开展了深入的研究［9-12］。目前，在LCSLM相位调制领域的研究已经比较成熟。2009年，西班牙F.Feng等人利用LC-SLM作为波前校正器对自由空间光通信系统进行了像差校正，通过系统像差的校正提高了通信系统的性能［13］。2010年，浙江师范大学信息光学研究所林培秋等人提出了利用LC-SLM的双折射特性模拟变焦透镜的方法，通过计算机生成的相息图来控制对入射光波的调制，改变衍射距离实现变焦透镜功能［14］。2018年，长春理工大学齐冀等人通过将计算机数值模拟出不同的相位灰度图加载到LC-SLM中，LC-SLM既可以作为凹透镜与一个焦距已知的凸匹配透镜配合使用，又可以校正像差，实现了激光的高质量连续变倍率扩束［15］。2020年，长春理工大学倪小龙等人通过计算激光相干度与激光束散角的关系，提出了一种利用LC-SLM控制激光相干度，精确控制激光束散角的方法［16］。以上研究大多数将LC-SLM应用于像差校正及变焦透镜，尚未用于激光束散角调控领域。

在分析总结上述研究成果的基础上，本文提出了基于LC-SLM的激光通信系统激光束散角控制系统方案，在发射端对通信激光束散角进行调控。利用LC-SLM构建变焦透镜，将相位灰度图加载到LC-SLM中，与固定焦距匹配透镜离焦配合，实现对激光束散角大小的控制。此方法无需机械移动LC-SLM与匹配透镜间的距离，反应速度快并且操作方便，能够动态灵活地控制激光束散角。

2 基于LC-SLM的激光束散角控制原理

2.1 LC-SLM实现光学变焦的原理分析

由于液晶的双折射特性，经过液晶分子后的折射光会分为两束，其中一束光的折射率为no，为寻常光遵循折射定律；另一束光的折射率为ne，为非寻常光不遵循折射定律。LC-SLM是一种通过产生光程差来对光波调制的器件，由于受外加信号驱动，液晶分子指向发生偏转导致折射率发生变化。光程差Δφ为：

式中，d为LC-SLM中液晶分子层的高度，λ为入射光的波长。

因为液晶具有上述特性，通过外加驱动信号可以改变液晶分子指向产生光程差，实现对入射光的调制。通过编码相应的相位函数生成相位灰度图，将相位灰度图导入到LC-SLM上，来自HDMI接口的驱动信号单独控制LC-SLM上的每个像素，导入的相位灰度图与LC-SLM上的每个像素一一对应并转换成电压，在LC-SLM内部产生电场，变化了液晶层的光学特性。因为像素之间的控制是相互独立的，因此可以通过导入不同灰度变化的相位图来控制每个像素的电压值。动态地改变加载的透镜相位函数的焦距，可以实现可编程变焦透镜以代替传统透镜实现透镜的基本作用［17-18］。

在透镜的孔径不是无限大的情况下，透镜的透过率函数可以表示为：

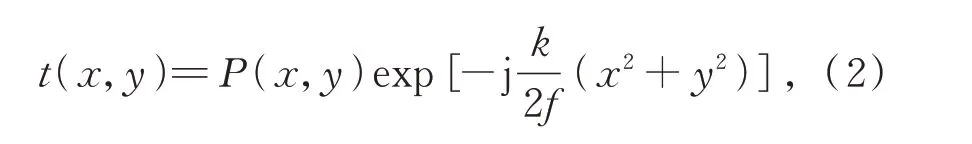
其中，f是透镜的焦距，P(x，y)是透镜孔径函数。当入射光在透镜的孔径内时，P(x，y)为1；当入射光不在透镜的孔径内时，P(x，y)为0。y2)]为透镜的相位因子，透镜对入射光的调制作用取决于透镜调制因子［19-20］。透镜的相位分布函数为：

由于LC-SLM是衍射光学元件，当相位调制量超过2π时，要对相位分布函数进行周期化处理。根据LC-SLM的调制特性对相位取模和和量化运算，上式中k=2π/λ，所以周期化后的分布函数为：

其中，fLC-SLM是LC-SLM模 拟 的 透 镜 焦距，mod2π表示对2π的取模运算，λ为入射光波的波长。所以欲实现LC-SLM的透镜变焦功能，只需改变fLC-SLM的值，将不同fLC-SLM的相位灰度图加载到LC-SLM中，改变LC-SLM内的液晶分子偏转方向，导致模拟透镜的折射率发生改变，完成光学变焦功能［21-22］。

2.2 激光束散角调控及测量原理

以激光通信为应用背景，束散角的控制原理如下：当束散角不发生改变时，LC-SLM模拟透镜的焦点和匹配透镜的焦点在同一位置上，根据准直原理，在理想环境下，最终出射的激光束散角控制变化量为0，入瞳直径和出瞳直径大小相等。光路原理图如图1和图2红色线所示。

当要对束散角进行控制时，只改变模拟透镜的焦距fLC-SLM，LC-SLM与匹配透镜间距离不变。此时，两透镜不再共焦。如果fLC-SLM变大时，焦点在初始焦点的右侧，fLC-SLM2＞fLC-SLM1，匹配透镜的焦距flens、LC-SLM与匹配透镜之间的距离都是恒定不变的。入射光源为高斯光束，经过LCSLM反射后，透过匹配透镜，根据近轴光路原理可知，如图1所示，光线偏离光轴，束散角增大，对激光束散角有调控作用。

图1 激光束散角增大控制原理图Fig.1 Diagram of laser beam divergence angle increase control principle

当fLC-SLM2＜fLC-SLM1时，LC-SLM模拟 透镜的焦点在初始焦点的左侧，其他条件不变，激光经过LC-SLM和匹配透镜后，光线偏向光轴，如图2所示，束散角减小。根据近轴光线方程和三角函数关系，得到束散角变化量的理论值。

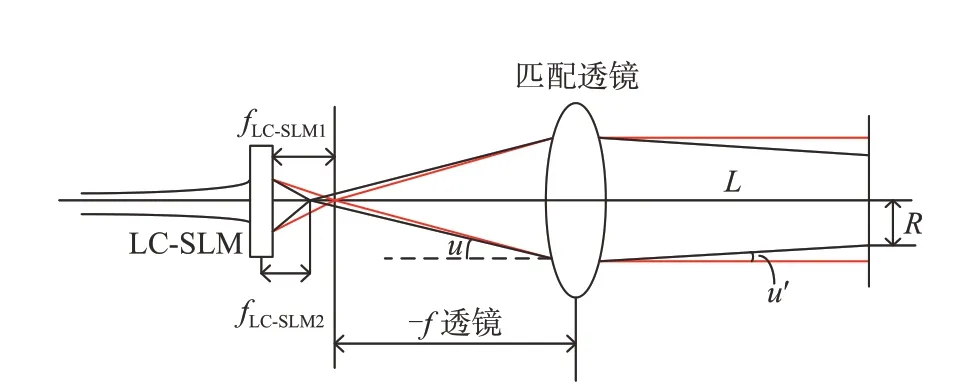
图2 激光束散角减小控制原理图Fig.2 Diagram of laser beam divergence angle decrease control principle

n′=1和n=1分别为光学系统两端折射率，u′和u分别为光线在匹配透镜两端的偏移角，r为匹配透镜的半径，式中光焦度φ=1/flens，flens为匹配透镜的焦距，故推出接收端光线偏移角的大小为：

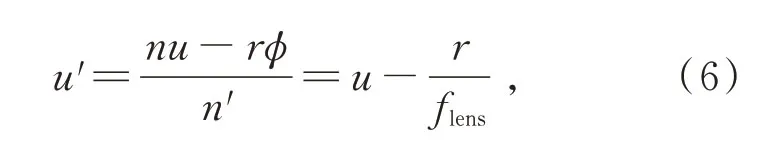
其中，匹配透镜发射端光线偏移角为

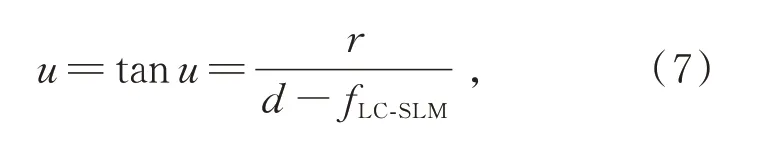
其中，d为SLM与匹配透镜之间固定距离，fLC-SLM为LC-SLM的焦距。经过以上调控系统后的激光束散角变化值θ为：

相机作为探测装置接收经过束散角控制系统调控后的激光，根据激光束散角测量原理计算束散角变化值，与束散角的理论变化值进行对比，分析激光束散角控制系统的误差。由于光束存在一定的束散角，经过汇聚透镜后在焦平面上形成一个弥散斑，设光束束散角为θ′，弥散斑直径为Dc，汇聚透镜的直径为D，根据弥散斑直径和汇聚透镜焦距可以计算出激光束散角的值（图3）［23-24］。

图3 激光束散角测量原理图Fig.3 Principle diagram of laser beam divergence angle measurement

根据牛顿公式：

由三角形相似定理可知

故推出激光束散角的大小为

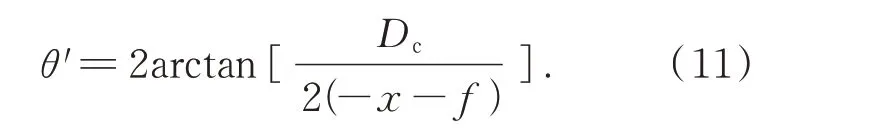
将式（9）和式（10）带入到式（11）中，得到简化的激光束散角表达式：

由于激光束散角很小，所以可以进一步简化为

根据以上公式可以得出，已知汇聚透镜的焦距大小，以及在汇聚透镜焦平面上测得的激光光束弥散斑直径大小，即可测得实际激光光束束散角的大小［25］。

3 实验与结果分析

3.1 基于LC-SLM的光学变焦性能实验验证

为验证LC-SLM能够实现光学变焦透镜功能，选用美国Meadowlark optics公司的LC-SLM构建了基于LC-SLM的光学变焦系统，其具体性能参数如表1所示。根据相位灰度图生成原理，分别生成对应95，100，105 mm焦距光学系统的相位灰度图。从生成的相位灰度图可以看出，越向外环带越密集，当外围环带过于密集时，会影响LC-SLM的调制效果。由于LC-SLM要求相邻像素间最大的相位差为π，为了减小LC-SLM相位调制的误差［26］，fLC-SLM应该满足下面的条件：

表1 空间光调制器性能参数Tab.1 Performance parameters of spatial light modulator

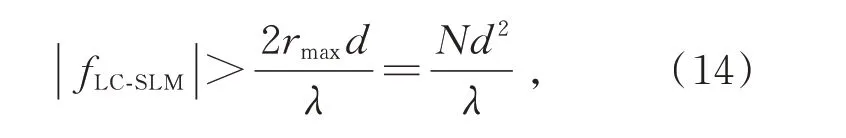
式中N为液晶的像素数量，d为像素之间的间隔距离，λ表示激光的波长，本文选用波段为1550 nm的激光器实验。经过计算，fLC-SLM最好大于63 mm。

1550nm激光器出射的激光经过LC-SLM反射后由接收屏接收光斑，将对应100 mm焦距光学系统的灰度图加载到LC-SLM上，在焦平面处观察到最小最亮的光斑，而在95 mm和105 mm处都是比100 mm处直径大的弥散斑，如图4所示，验证了LC-SLM具有模拟变焦透镜的能力。

图4 不同焦距光斑图Fig.4 Spot map of different focal lengths

3.2 基于LC-SLM的光束束散角控制系统构建与性能验证

基于前面的分析和验证结论，本文搭建了如图5所示的激光束散角控制实验系统。激光器发射波长为1550 nm的激光，经过准直扩束装置后得到的激光直径为7 mm，再通过偏振片，得到满足LC-SLM调制条件的线性偏振光。LC-SLM与匹配透镜共同组成激光束散角控制单元，将计算机生成的相位灰度图导入LC-SLM，经LC-SLM反射后的激光透过匹配透镜，激光束散角发生变化。最终由相机接收光斑，相机的性能参数如表2所示，根据激光束散角测量原理，计算光斑直径和束散角的变化。

图5 激光光束束散角控制系统方案Fig.5 Schemetic diagram of laser beam divergence angle control system

表2 相机性能参数Tab.2 Camera performance parameters

为满足通信信号光束散角大小的要求，激光束散角控制系统的调制精度要足够高，这就对匹配透镜的孔径和焦距有一定的限制条件。根据激光束散角的调控原理，选用直径为5 mm，焦距flens为500 mm的匹配透镜，控制精度为100 μrad。选定LC-SLM的初始焦距fLC-SLM1为100 mm，整个调控过程LC-SLM和匹配透镜之间的距离d恒定，d=flens+fLC-SLM1=600 mm。此时，LC-SLM模拟变焦透镜的焦点与匹配透镜的焦点在同一位置，激光准直出射，对激光束散角没有控制作用。以初始焦距fLC-SLM1为界，将计算机生成焦距分别为80，85，90，95，105，110，115，120 mm的相位灰度图导入LC-SLM，其他参数不变，由相机接收光斑直径变化，其中P为光斑像素数量（图6）。

图6 LC-SLM不同焦距的相位灰度图及对应光斑图Fig.6 Phase gray-scale images and corresponding spot images of LC-SLM with different focal lengths

利用MATLAB图像处理的方法对光斑图进行亮度调节、二值化处理、中值滤波、形态学处理及圆拟合来计算光斑的直径。当fLC-SLM取不同值时，对不同焦距下测得的光斑直径取10次测量的平均值计算束散角变化量。

不同焦距下的实验数据与理论束散角变化值对比结果如表3所示，束散角变化量绝对误差折线如图7所示。实验数据与理论变化值存在一定偏差，误差主要来源于接收光斑直径的计算及LC-SLM调制产生的像差。液晶波片消色差的能力不强，折射率随波长变化而变化，与波长相关的校准至关重要。LC-SLM的像素间距非常小，单片镜片匹配透镜会引入球差，也会对束散角控制系统引入一定误差。

图7 绝对误差折线图Fig.7 Absolute error line chart

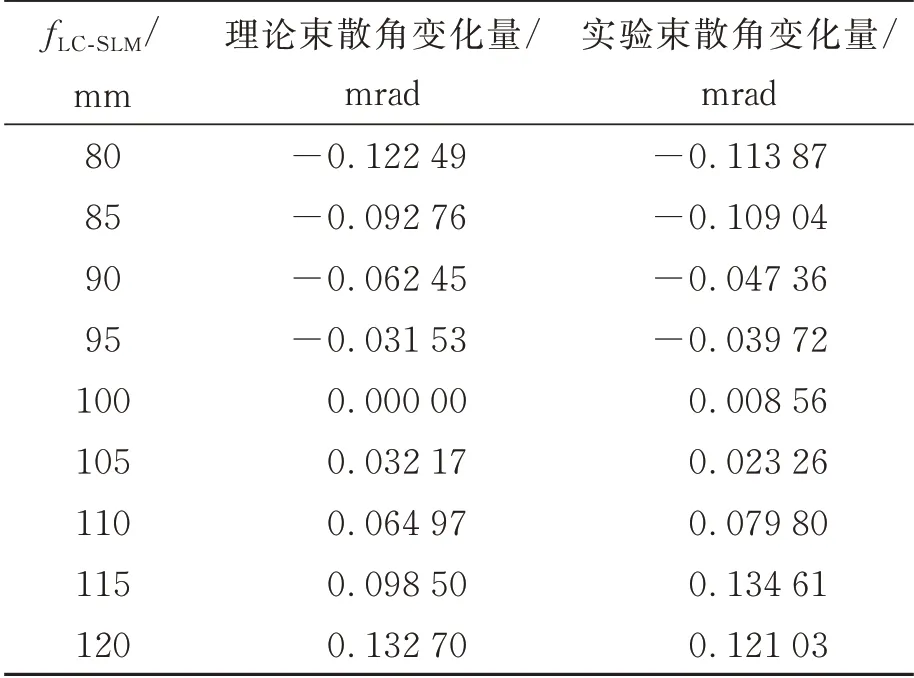
表3 束散角变化理论值与实验值Tab.3 Theoretical and experimental values of beam dispersion angle variation

根据表3绘制束散角变化曲线（图8），在fLC-SLM取100 mm时，激光束散角控制系统对激光束散角没有调控作用，但由于以上误差导致仍然存在控制量。随着fLC-SLM由小到大变化，激光束散角变化量也成线性关系变化，实验束散角变化值贴近理论值，激光束散角控制系统RMSE=0.0175。可见，本文提出的方法能够灵活调控激光束散角。

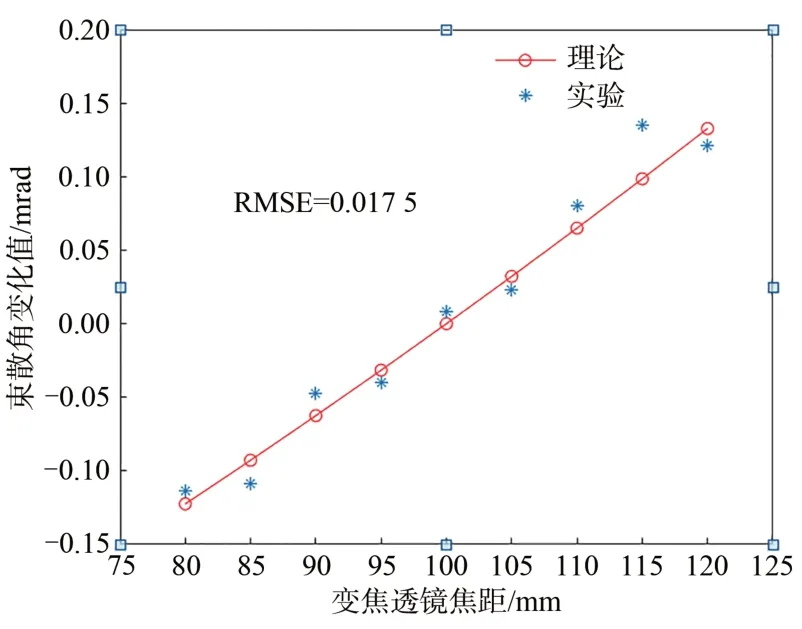
图8 束散角变化曲线Fig.8 Variation curve of beam dispersion angle

4 结论

本文提出了基于LC-SLM的激光束散角调控技术方案，对其调控原理和具体性能进行了分析，并构建了实验系统对光束束散角调控性能进行了验证。通过向LC-SLM导入不同的相位灰度调制图，实现LC-SLM光学变焦透镜功能。将LC-SLM与固定焦距匹配透镜共同构成束散角控制单元，即可通过改变LC-SLM模拟透镜的焦距实现激光束散角的实时调控。实验结果表明，激光束散角调控的偏差在5%以内，RMSE为0.0175。

基于LC-SLM的激光束散角调控技术解决了传统激光光束束散角控制结构复杂、操作繁冗，精度不高的问题，简化了操作过程并提高了控制精度，为空间激光通信系统中通信光束参数的动态调控提供了有效的技术支撑。