长服役期橡胶密封性能分析与寿命评估

王莉娜，史纪军，李 征，孙立臣，孙 伟，孟冬辉，张海峰，任国华，郭 琦

（北京卫星环境工程研究所，北京 100094）

0 引言

空间站是长期在轨运行的有人值守的大型载人航天器，其密封舱体为航天员在地外生存提供了安全、稳定的环境，一旦空间站的密封结构发生泄漏，将直接影响空间站的正常运行，威胁航天员的生命安全，导致灾难性的航天事故。空间站系统中的橡胶密封结构属薄弱环节，即橡胶密封的寿命会成为掣肘在轨航天器系统长寿命的关键因素之一。因此，近年来关于橡胶密封性能的理论分析和试验工作受到广泛关注。

Coons 和Liu 等采用热氧老化试验箱开展硅橡胶材料圆柱试样热氧老化试验，对比热氧老化试验前、后硅橡胶压缩永久变形、应力-应变本构关系间的差异，获得热氧老化效应对硅橡胶力学性能的影响规律。Kong 和刘巧斌等测试橡胶圆柱试样热氧老化前、后的压缩永久变形，并采用最小二乘法对试验数据进行处理，绘制阿伦尼乌斯曲线以预测橡胶材料本体的寿命。王莉娜等将应力松弛效应计入构建的球头-锥面密封结构性能分析有限元模型中，获得接触副间的接触压力和接触宽度随蠕变时间的变化规律；然后结合Roth 泄漏模型，获得球头-锥面密封结构性能的劣化规律，进而实现对其寿命的预测。Persson 和Li 等分别基于渗透理论和分形理论建立静密封接触副间的初始表面微观形貌模型，分析压力载荷作用下接触副间的接触性能，并构建静密封结构微观泄漏模型，实现对密封结构性能的仿真计算。

可以看到，现有研究中针对橡胶密封寿命的评估大都集中于对橡胶材料本体寿命的评估，使得其寿命评估精度有一定局限性。载人空间站舱内的主要气体成分与地面空气成分基本相同，而相较于空气中的其他气体成分，氧气对橡胶材料性能的影响较大，因此本文采用热氧加速老化的试验方法对空间站密封结构的性能进行评价。首先基于时温等效理论构建考虑热氧老化效应的橡胶密封性能分析有限元模型，计算其宏观接触性能；然后在不同热氧老化效应条件下，建立橡胶密封计算的平均接触压力与试验测试的泄漏率间的函数关系，以期实现对有长服役要求的橡胶密封泄漏率的快速预测。

1 热氧老化数学模型

1.1 时温等效理论

橡胶密封实际工作时一直处于压缩状态，因此可以(1-)作为其性能变化指标，其中为密封材料的压缩永久变形率。

橡胶材料性能变化指标与老化时间之间的函数关系可以表示为

式中：为常数；为与温度有关的性能变化速度常数；为常数，如果=1，则ln和之间具有线性关系。

式(1)中的可通过Arrhenius 方程表征为

式中：为频率因子；为材料的表观活化能；为理想气体常数；为老化温度。

在得到=(,)的表达式后，采用最小二乘法对试验数据进行拟合，可获得函数式中的各系数值。

Mooney-Rivlin 模型在超弹性力学研究中使用最为广泛，能描述大部分橡胶力学行为，经典二参数Mooney-Rivlin 本构模型的应变能密度表达式为

1.2 热氧老化试验前、后橡胶材料的本构关系

式中：和为待定力学性能常数；为描述材料压缩性能的系数；为体积比；和为应变不变量。

根据测试的热氧老化前、后橡胶材料试样的本构关系可拟合出不同性能变化指标下Mooney-Rivlin模型的系数和，详见表1。再将这一物性参数计入构建的橡胶密封性能分析有限元模型中，可实现考虑热氧老化效应的橡胶密封性能分析。

表1 不同性能变化指标下Mooney-Rivlin 模型的系数Table 1 Coefficients of Mooney-Rivlin model under different performance change indexes

1.3 橡胶材料寿命预测与评估

表2 为热氧老化试验条件下橡胶圆柱试样压缩永久变形的测试结果，从表中可以看出随老化温度的升高和老化时间的延长，橡胶试样的压缩永久变形虽有波动，但整体呈现增大的趋势。造成这种现象的主要原因与高分子橡胶材料制备的试样具有显著个体差异有关。

表2 不同老化效应下橡胶试样的压缩永久变形Table 2 Permanent compressive deformation of rubber sample under different aging temperatures

表3 所示为橡胶材料性能变化指标平均值的预测结果，并以此为基础构建考虑热氧老化效应的橡胶密封接触性能分析理论模型。

表3 橡胶性能变化指标Pi 平均值的预测Table 3 Prediction of average value of rubber performance change index Pi

2 考虑热氧老化效应的O 形橡胶接触性能分析

2.1 O 形橡胶密封接触性能分析有限元模型

根据O 形橡胶密封的结构参数及工况参数，建立橡胶密封接触性能分析有限元模型如图1 所示，其性能分析的边界条件为：位置1 处施加方向上的位移激励（模拟橡胶密封圈压缩变形量）；位置2处施加气体压力载荷；密封槽3 处施加和方向位移约束。

图1 橡胶密封接触性能分析有限元模型Fig. 1 FEM model for rubber seal performance analysis

将老化试验前、后橡胶试样的应力-应变本构关系（表1）应用于橡胶密封接触性能分析理论模型中，可实现热氧老化效应影响的嵌入，即实现考虑热氧老化效应的橡胶密封接触性能分析。

2.2 考虑热氧老化效应的O 形橡胶密封接触性能分析结果

依据表4 中橡胶密封的结构、材料和工况参数，建立考虑热氧老化效应的O 形橡胶密封接触性能分析模型，探讨不同压缩率和性能变化指标对其性能的影响，其中流体介质为空气。

表4 橡胶密封结构和工况参数Table 4 Structural and working parameters of rubber seal

2.2.1 不同压缩率下O 形橡胶密封的接触性能

压缩率对O 形橡胶密封接触压力的影响分析结果如图2 所示，可以看出，O 形橡胶密封的接触压力随压缩率的增大而增大。但过大的压缩率会加速橡胶材料的老化进程，缩短橡胶密封的寿命；且大的压缩率会增大密封系统的螺栓预紧力，将导致螺栓材料蠕变速率增大，改变螺栓再次预紧的时间。从图中还可看出，依初始状态（即橡胶材料未受老化效应的影响时，其性能变化指标为100%）、性能变化指标为70%及50%的顺序，橡胶密封的接触压力随之降低。这是因为老化效应会使橡胶材料变硬而使其回弹性能降低，表现为O 形橡胶密封接触压力的减小。

图2 压缩率对O 形橡胶密封接触压力的影响Fig. 2 Influence of compression rate on the contact pressure of O-ring rubber seal

与图2 相对应，图3 所示为压缩率对橡胶密封接触宽度的影响分析。可以看出，O 形橡胶密封的接触宽度随压缩率的增大而增大，表明橡胶密封性能的可靠性有所提升；相同压缩率下，依初始状态、性能变化指标为70%及50%的顺序，O 形橡胶密封的接触宽度随之减小，这同样是因为老化效应使橡胶材料变硬从而造成其回弹性能降低。

图3 压缩率对O 形橡胶密封接触宽度的影响Fig. 3 Influence of compression rate on the contact width of O-ring rubber seal

2.2.2 不同性能变化指标下O 形橡胶密封的接触性能

图4 为性能变化指标对O 形橡胶密封接触压力的影响，从图中可以看出，O 形橡胶密封接触压力随性能变化指标的减小而减小，这是因为老化程度的增加使橡胶材料的回弹性能降低，直接表现为橡胶密封接触压力减小。从图中还可看出，压缩率为30%的橡胶密封的接触压力大于压缩率为25%的橡胶密封的接触压力。

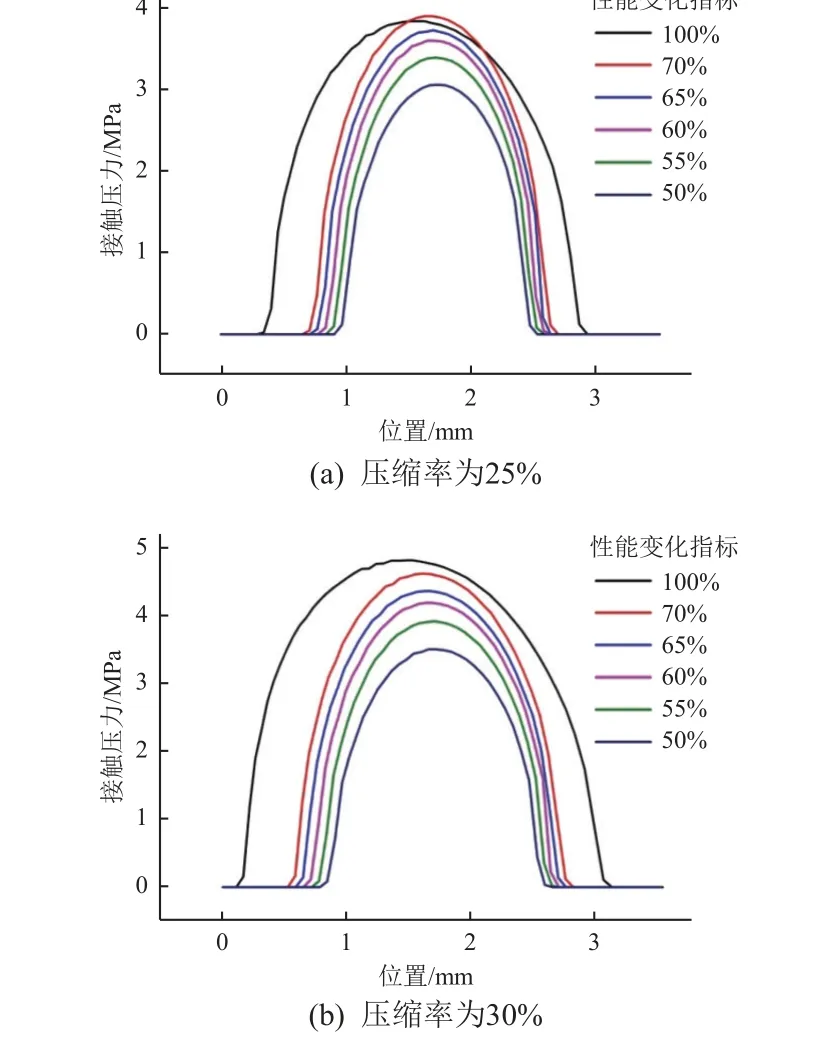
图4 性能变化指标对O 形橡胶密封接触压力的影响Fig. 4 Influence of performance change index on the contact pressure of O-ring rubber seal

图5 为性能变化指标对O 形橡胶密封接触宽度的影响，从图中可以看出，随着性能变化指标的减小，2 种压缩率下橡胶密封的接触宽度均会减小，这主要与老化程度的增加影响橡胶材料的回弹性有关。从图中还可以看出，不同性能变化指标下，压缩率为30%的橡胶密封的接触宽度均大于压缩率为25%的橡胶密封的接触宽度。

图5 性能变化指标对O 形橡胶密封接触宽度的影响Fig. 5 Influence of performance change index on the contact width of O-ring rubber seal

3 O 形橡胶密封接触性能与其密封性能间对应关系

3.1 热氧老化试验前、后O 形橡胶密封的性能测试结果

橡胶密封圈试样的截面直径为3.55 mm，密封圈内径为46 mm，计算得到其圆周长度为144.44 mm。试验供给的流体压力与载人空间站密封舱内的气体压力相同，均为0.1 MPa。

橡胶密封泄漏率测试的具体步骤如下：

1）将橡胶密封圈安装于制备的检漏工装中，连接好管路，并置于真空罐中；

2）先由机械泵将真空罐内的真空度抽至10 Pa左右，然后开启分子泵，将真空罐内的真空度抽至4.5×10Pa；

3）开启氦质谱检漏仪，测试检漏的本底噪声，计算最小可检测漏率，并用标准漏孔对检漏系统进行标定；

4）将高纯氦气充入安装有橡胶密封圈的检漏工装内，待氦质谱检漏仪读数稳定时记录检漏结果；

5）通过比对法，计算获得橡胶密封的泄漏率。

性能变化指标100%（即初始状态）、70%、65%、60%、55%和50%分别对应橡胶密封圈常温下贮存0 年、1.9 年、3.1 年、5.0 年、7.9 年和12.5 年。

在压缩率为25%条件下，采用氦质谱真空检漏方法，测试不同性能变化指标的O 形橡胶密封的氦气（He）泄漏率，结果如图6 所示。从图中可以看出，O 形橡胶密封的泄漏率随性能变化指标的减小（即随服役时间的延长）呈现出先较快增长而后缓慢增长的变化趋势。造成这种现象的原因在于，热氧老化效应影响下，橡胶密封局部接触区域的材料出现塑性变形而丧失回弹性能，造成橡胶密封性能的劣化。

图6 橡胶密封泄漏率随贮存时间的变化Fig. 6 Leakage rate of O-ring rubber seal against the storage time

在压缩率为25%条件下，O 形橡胶密封计算的平均接触压力与试验测试的泄漏率间的关系曲线如图7 所示，可以看出，随着平均接触压力的增大，O 形橡胶密封的泄漏率呈现非线性减小的趋势。根据该曲线拟合的泄漏率与平均接触压力的函数关系式为

图7 橡胶密封泄漏率与其平均接触压力间的关系曲线Fig. 7 Relationship between the leakage rate of rubber seal and its average contact pressure

3.2 O 形橡胶密封计算的平均接触压力与试验测试的泄漏率间的关系

4 O 形橡胶密封寿命评估与试验验证

4.1 O 形橡胶密封泄漏率预测结果与试验结果的对比

这部分研究内容的思路为：先采用构建的考虑热氧老化效应的橡胶密封性能分析有限元模型计算其平均接触压力，然后采用公式(4)对橡胶密封的泄漏率进行快速预测，再对预测结果与试验结果进行对比。

图8 为O 形橡胶密封泄漏率的理论预测结果与试验结果的对比情况（橡胶密封泄漏率预测值与试验值间的误差均小于10%，满足精度要求），可以看出，随贮存时间的逐步延长，O 形橡胶密封泄漏率的预测值与试验测试值均会增大，表明老化效应会造成橡胶密封性能劣化。从图中还可以看出，O 形橡胶密封的泄漏率随压缩率的增大而减小，这主要是因为橡胶密封的接触压力随压缩率的增大而增大，而较大的接触压力有助于提升橡胶密封接触副间的紧密结合程度，从而使橡胶密封的泄漏率减小。但橡胶材料的压缩率大小与其老化速度成正比，压缩率增大必然会缩短橡胶密封的寿命。此外，从图中还可以看出：压缩率为15%时，橡胶密封泄漏率预测值较试验值小；而压缩率为30%时，橡胶密封泄漏率预测值较试验值大。造成这种现象的主要原因在于，橡胶密封泄漏率预测公式是在压缩率为25%的条件下获得的，而在其他的压缩率下，橡胶密封相接触的两粗糙面间的微观接触状态会发生一定程度的变化。

图8 橡胶密封泄漏率预测结果与试验结果的对比Fig. 8 Comparison between prediction results and test results of rubber seal leakage rates

4.2 O 形橡胶密封寿命评估

试验获得氦气（He）通过O 形橡胶密封的泄漏率随老化时间延长的变化规律，再拟合公式并外推，可实现对橡胶密封寿命的预测。为提高预测精度，分别拟合不同压缩率（15%、25%、30%）下橡胶密封寿命评估的数学模型，其中的单位为s：

进行计算，式中：2π为橡胶密封圈周长，mm；为橡胶密封圈每mm 长度对应的泄漏率。

本文所提出的橡胶密封寿命预测方法具有通用性，可用于不同截面尺寸橡胶密封圈的密封寿命评估。

5 结论

1）采用构建的考虑热氧老化效应的O 形橡胶密封接触性能分析有限元模型，分别研究压缩率和性能变化指标对橡胶密封接触性能的影响。结果表明，随着压缩率和性能变化指标的减小，橡胶密封的接触压力和接触宽度均会减小。因此，有长服役期要求时，除应该根据实际密封要求选择合适的压缩率外，热氧老化效应对密封性能的影响不能被忽略。

2）采用橡胶密封泄漏率与其平均接触压力间的拟合公式，对不同压缩率下橡胶密封的密封性能进行预测，并与试验测试的泄漏率进行对比，结果表明2 种结果间的误差均小于10%，满足精度要求。这一研究方法还可用于对其他不同结构和工况条件下的O 形橡胶密封的密封性能进行快速预测，具有较高的工程应用价值。

3）根据O 形橡胶密封性能随老化时间延长的变化规律，建立橡胶密封寿命评估数学模型，经外推可实现对有长服役期要求的橡胶密封寿命的精确预测。这一研究方法同样适用于其他密封圈截面尺寸与工况下的橡胶密封寿命预测。