底水油藏水平井分段见水时间计算方法研究

张际久 齐国明 李 东 李疾翎

中海油田服务股份有限公司油田技术事业部,天津 300459

0 前言

水平井可以大幅度提高井筒与油层的接触面积,在薄层、低渗透、底水油气藏开发中应用广泛。采用水平井开发底水油藏,在投产前根据井眼轨迹和钻遇情况,较为准确地预测水平段不同部位的产量和见水时间,进而针对性地优化完井方案;在投产后根据生产情况预测底水脊进形态,为生产制度优化调整提供依据和参考,这样可有效提升水平井的精细化管理水平和综合开发效益。

目前对于水平井分段产量的影响因素和计算方法已有较多成熟的研究成果[1-10],但是关于水平井见水时间的计算方法,目前的研究主要考虑产量、水平段长度等因素的影响[9-17],很少考虑井眼轨迹高低变化因素的影响。程林松等人[10]分析了水平井水平段长度、距离底水高度、地层非均质性等因素对产量、见水时间的影响,但是没有考虑井筒压降、井眼轨迹等影响因素。李立峰等人[11]研究了井筒压降对底水油藏水平井见水时间的影响,分析了见水时间随水平井产量、水平段长度等因素的变化规律,但同样没有考虑井眼轨迹的影响。目前关于水平井见水时间的研究一般假设水平段完全水平,但实际的水平井井眼轨迹是存在高低起伏的,这一因素对产量的影响较小,但是对见水时间的影响较大,显然水平段在距离底水近的部位见水时间更短。

水平井见水时间除了受井眼轨迹影响外,还与分段产量、储层非均质性、渗透率各向异性等因素密切相关。在水平井不同部位,受非均质性和井筒压降的影响,底水向上锥进的速率不同。在水平段同一部位,与井筒的距离不同,底水向上锥进的速率也不同,这些因素都给计算水平段不同部位的见水时间带来了很大挑战。

本文在前人研究成果的基础上,基于稳定渗流理论,全面考虑了油藏物性变化、渗透率各向异性、水平井筒流动压降、井眼轨迹高低变化等影响因素,建立了底水油藏中流体运移的数学模型,研究了流体运移速度与其和水平段的距离之间的关系,并积分得到了计算水平井各部位见水时间的解析解。通过该解析解不仅可以预测水平段各部位的产量和见水时间,还可以在水平井生产一段时间后,直观显示出水平段下方的水脊形态。经过对比,本文所建立方法的计算结果与王家禄、任超群等人[18-19]采用实验装置模拟得到的水脊形态、见水时间规律一致。

1 分段产量计算

建立底水油藏水平井生产稳定渗流物理模型,假设条件如下:油藏流体为不可压缩流体;流体在油藏中的流动为稳定的达西渗流;将水平井分为N段,每个单元段可看作线汇且单元段内的流量均匀分布。

1.1 底水油藏压力分布及产量求解

底水油藏水平井生产示意图见图1。

图1 底水油藏水平井生产示意图Fig.1 Production diagram of horizontal well in bottom water reservoir

如图1所示,油层顶部为封闭边界,油层底部油水边界为定压边界,位于xoy平面。水平井第i段(1 ≤i≤N，N为水平井分段数)长度为Li,跟端坐标为(x1i,y1i,z1i),趾端坐标为(x2i,y2i,z2i)。则水平井第i段以产量qi生产后,油藏中任意一点(x,y,z)产生的势为[1]:

(1)

其中:

式中:Φi(x,y,z)为水平井第i段生产在油藏中任意一点产生的势,m2/ks;Ci为水平井第i段生产势函数的积分常数,m2/ks;qi为水平井第i段产量,m3/ks;Li为水平井第i段长度,m;φi(x,y,z)为水平井第i段的跟端和趾端与油藏中任意一点的距离的函数,m-1;n为根据镜像法则虚拟的镜像井数量,整数;ξi(n1in,n2in)为油藏中任意一点与水平井第i段第n个镜像跟端和趾端的距离函数；h为油层厚度,m;η1in和η2in分别为水平井第i段的第n个镜像的跟端和趾端的z坐标,m;r1in和r2in分别为油藏中任意一点到水平井第i段的第n个镜像的跟端和趾端的距离,m。

根据势的叠加原理[20],水平井全部N个水平段生产在油层中产生的势为:

(2)

式中:Φ(x,y,z)为水平井全部分段生产在油藏中任意一点产生的势,m2/ks;N为水平井分段数,自然数。

根据势函数的定义:

(3)

式中:k为地层渗透率,D;μ为地层原油黏度,mPa·s;p(x,y,z)为油藏中任意一点的地层压力,MPa;ρ为储层流体密度,kg/m3;g为重力加速度,为9.8 m/s2。

根据式(1)～(3)可以得到:

(4)

式中:Φie为水平井第i段生产时底水界面处的势,m2/ks;pe为油水边界处地层压力,MPa。

式(4)对于油层中任意一点都成立。在水平井第j段(1 ≤j≤N)中心井壁处,设其坐标为[(x1j+x2j)/2,(y1j+y2j)/2, (z1j+z2j)/2-rw],式(4)也成立,因此有:

(5)

式中:rw为井眼半径,m;Φij为水平井第i段生产时在第j段中心井壁处产生的势,m2/ks;kj为水平井第j段平均地层渗透率,D;pwj为水平井第j段处的井底流压,MPa;zj为水平井第j段中心处的z坐标,m。

结合式(1)、式(5)写成以下矩阵形式更为直观:

(6)

其中:

式中:λj为水平井第j段的流度和生产压差的函数,m2/ks;φij为水平井第i段的跟端和趾端与水平井第j段中心的距离的函数,具体见式(1),m-1;φie为水平井第i段的跟端和趾端与底水界面上任意一点的距离的函数,m-1。

式(6)左边的系数矩阵是严格的对角占优矩阵,可以通过Gauss-Seidel迭代法求解,迭代公式为:

(7)

式中:m为迭代次数,自然数。

输入一组井底流压pwj数值后,即可迭代求解得到水平段每一段的单位长度产量。

1.2 水平井筒内流动压降

在水平井筒中,流体克服流动摩阻从趾端流向跟端,必然会消耗一部分能量,产生一定的压降。已有较多学者研究了该压降的计算方法和对水平井产出的影响[2,21-22]。本文采用的裸眼完井水平井段井筒压降的计算公式为[2,23]:

(8)

式中:Δpwj为水平井第j段的井筒压降,MPa;Cfr为考虑流入影响的水平井筒壁面摩擦校正系数;fj为水平井第j段壁面摩擦系数;D为筛管直径,m;Qj为水平井筒中从趾端到第j段的累积流量,m3/ks。

1.3 渗透率各向异性影响

一般情况下,储层渗透率会存在各向异性(kh≠kv),定义:

(9)

(10)

用βh、βz分别替换h、z,考虑渗透率各向异性的影响。

式中:kh、kv分别为储层水平、垂直渗透率,D;β为渗透率各向异性系数。

2 分段见水时间计算

如果采用直井开发底水油藏,底水突进会呈现“水锥”形态,如果采用水平井开发底水油藏,底水突进会呈现“水脊”形态[12]。把水平井分为N段,如果N足够大,水平井的每一段都可以假设成为一口直井。因此,“水脊”也可以视为N个“水锥”的叠加。

根据式(1),水平井第i段生产后,地层中任意一点z方向上的渗流速度为:

(11)

其中:

式中:vzi(x,y,z)为水平井第i段生产引起的地层中某一位置流体的运移速度,m/d；δi(n1in,n2in)为油藏中任意一点与水平井第i段的第n个镜像跟端和趾端的距离的函数；dz为地层中流体运移的单元距离，m。

根据叠加原理[20],地层中任意一点(x,y,z)在z方向上的渗流速度为:

(12)

式中:vz(x,y,z)为水平井稳定生产时地层中某一位置流体的运移速度,m/d。

由于:

(13)

式中:dt为流体运移单元距离所需的时间,d;φ为地层孔隙度。

设水平井段上某一位置坐标为(xw,yw,zw),式(13)积分得到水平井段上任意一点的见水时间为:

(14)

式中:T(xw,yw,zw)为水平井段上某一位置的见水时间,d。

式(14)中的积分函数形式复杂,确定其原函数十分困难。研究底水油藏水平井不同部位的底水运移速度规律，通过观察可以发现,流体运移速度vz(xw,yw,z)与其和水平段的距离Δz(Δz=zw-z)之间存在相关性很高的幂函数关系。地层中vz与Δz的关系图见图2,图2显示了在斜深2 115 m、2 400 m、2 610 m处底水向上运移的速度,这3个深度离底水界面的距离分别为5.2 m、5.2 m和6.4 m。

图2 地层中流体渗流速度与距离水平段距离的关系图Fig.2 Relationship diagram between reservoir fluid seepage velocity and distance from horizontal section

根据以上规律,式(14)可以改写成:

(15)

式中:c1、c2为与xw、yw、zw、qi等参数相关的常系数。

确定c1、c2的方法如下:选取水平井段上某一位置(xw,yw,zw)下方的两点,本文选取与水平段的距离分别为0.75zw和0.25zw的两点,即两点坐标分别为(xw,yw, 0.25zw)和(xw,yw, 0.75zw),计算其z方向上的渗流速度分别为vz1和vz2。则有:

(16)

(17)

式中:vz1、vz2为水平井下方与水平段距离分别为0.75zw和0.25zw位置处流体向上运移的速度,m/d。

式(15)积分,同时考虑渗透率各向异性的影响,则有:

(18)

通过式(18)就可以计算水平段任意位置的见水时间。另外,也可以计算水平井生产一段时间后水平段各部位的底水脊进距离,直观显示出水平井下方的水脊形态。式(15)积分并整理得到:

(19)

式中:tp为水平井稳定生产的时间,d;d(xw,yw,tp)为水平井稳定生产tp时间后,水平段某一位置下方的底水脊进高度,m。

3 实例计算

用以上方法对海上某底水油藏水平井进行模拟。该井水平段渗透率曲线及预测产液剖面图见图3，平均渗透率为718 mD，该井的其他参数如下:底水界面位于1 786 m,油层厚度9.1 m,平均孔隙度30%,油藏压力17.29 MPa,地层原油密度848.7 kg/m3,地层原油黏度18.68 mPa·s。水平段为2 098～2 734.9 m,钻头尺寸215.9 mm,裸眼筛管完井,筛管内径150.4 mm。井底流压15 MPa。

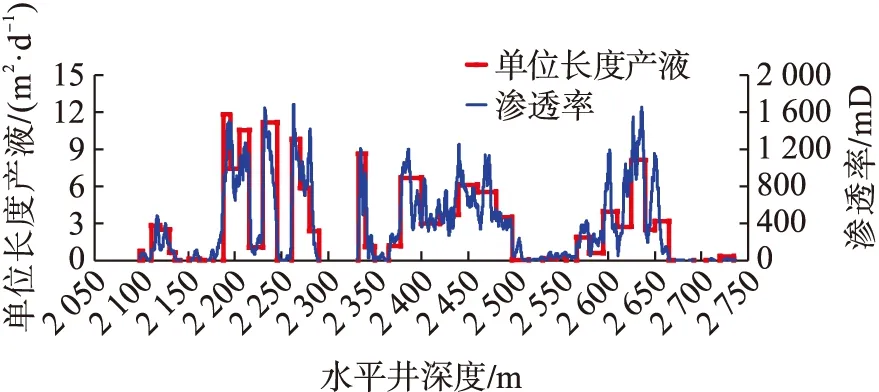
图3 某底水油藏水平井渗透率及产液剖面图Fig.3 Permeability and production profile of a horizontal well in bottom water reservoir

该井生产见水时间及水脊形态模拟结果见图4,图4显示投产后产量为1 694.9 m3/d,见水部位为2 187.7～2 215.4 m,见水时间为24.3 d。通过预测的投产20 d后的水脊形态可以看出,底水容易在水平段中部高渗部位提前突破,趾端和跟端的油水界面上升较慢,见水时波及区域较小,这与物理模拟观测到的见水时间规律一致。

该井实际投产后产量在1 237.5～1 614.9 m3/d之间波动,22 d后含水明显上升,与模拟结果差异较小,说明该模型的准确度较高。

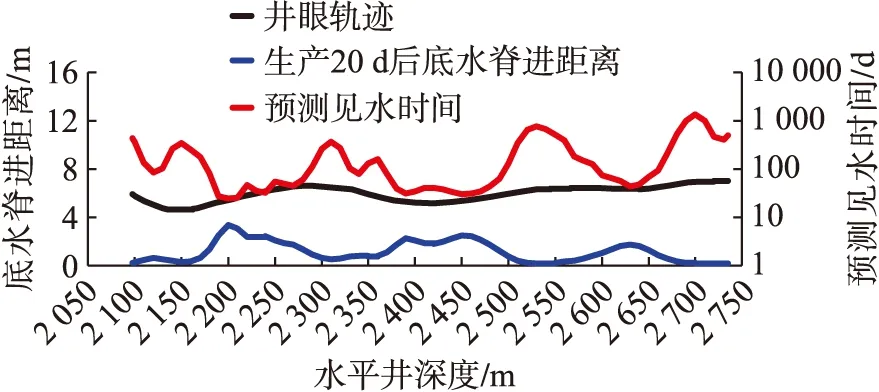
图4 某底水油藏水平井生产见水时间及水脊形态模拟结果图Fig.4 Simulation results of water breakthrough time and water coning shape of a horizontal well in bottom water reservoir

4 结论

1)基于稳定渗流理论,全面考虑油藏段物性变化、渗透率各向异性、水平井筒内流动压降以及井眼轨迹高低变化等影响因素,建立了计算水平井不同部位见水时间和底水运移距离的方法。

2)通过分析底水油藏中流体运移规律,发现流体向上运移速度与其和水平段的距离呈幂函数关系。

3)通过实际应用,证明本文所建方法的准确度和可靠性较强,与物理模拟方法得到的见水时间、水脊形态规律一致。

4)本文所建立方法可以为优化完井方案、调整生产制度等应用提供参考和依据,具有可推广性。