融合退化过程和谱分析的接触网检修模式优化研究

张鹏强

0 引言

接触网系统作为高速铁路牵引供电系统的关键设备，具有无备用、结构复杂、易受冲击等特点，检修维护工作对保障高铁系统的安全与效率至关重要[1]。随着我国高速铁路建设的快速发展，以周期修为主的维修模式未充分考虑高铁接触网系统的结构特点和服役条件，存在耗时长、效率低、工作量大、成本高昂等不足，已不能满足高铁接触网运营维护的需求[2，3]。

依托快速发展的接触网检测监测技术，将被动式的周期修改善为主动式的状态修，对于接触网系统维护具有重要意义。目前，接触网检修优化的研究主要以设备可靠性或设备状态为中心。前者基本目标是以最小资源消耗保持接触网设备的可靠性，在一定程度上增强了接触网系统维修作业的针对性[4，5]。后者将PHM 思想引入接触网运维领域，根据6C 检测数据对设备状态进行预测性诊断，并据此制定维修计划[6]。但以上思路的研究对象是单一类型的接触网设备，未能实现对维修资源的全面优化。

本文全面考量影响接触网系统运行状态的各类因素并分析其影响程度，建立合理的高速铁路接触网系统运行状态评价体系与退化模型，基于接触网系统运行状态制定主动维修策略，并结合谱分析优化计划修周期，使接触网系统维修作业更加科学与高效。

1 高速铁路接触网系统运行状态评价模型

1.1 接触网系统运行状态评价体系的构建

高速铁路接触网状态评价的目的是将接触网系统不同层级的多项指标加以综合得到其稳定度，然后对稳定度进行分析运算，从而对接触网系统进行整体性评价，确定接触网运行状态等级。接触网系统运行状态框架主要由3 个层面构成：决策目标是接触网运行状态，直接相关的一级指标为可靠性指标、可用性指标和可维修性指标，各一级指标下设相应的二级指标。接触网运行状态评价体系如图1 所示。

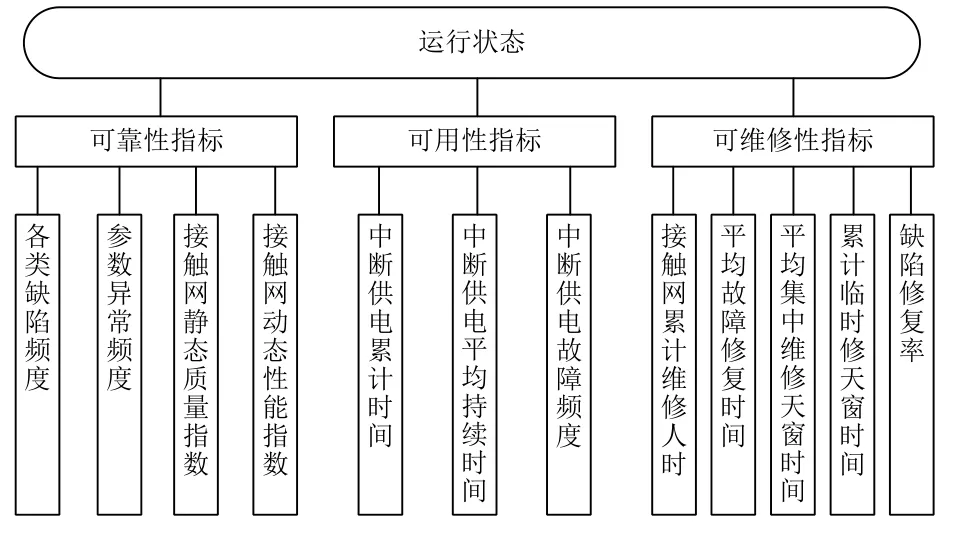
图1 接触网运行状态评价体系

可靠性指标指在给定的条件下和给定的时间区间内，接触网系统内各零部件及设备能完成要求的机械荷重、允许温升、载流量、规定电气作用等工作能力。主要考察接触网几何参数指标（如导高、拉出值）、平顺性指标（如硬点）、弓网受流性能指标（如弓网接触力、燃弧时间）以及接触网零部件失效情况。其下属二级指标包括各类缺陷频度、参数异常频度、接触网静态质量指数、接触网动态性能指数。

可用性指标指接触网系统在所要求的维修、管理等外部资源得到提供的情况下，在规定工况条件下，在给定的时间区间内可执行持续供电的能力。其下属二级指标包括中断供电累计时间、中断供电平均持续时间和中断供电故障频度。

可维修性指标是指使用规定的程序和资源进行接触网维修时，在给定的使用条件下，保持或恢复接触网系统或零部件能完成要求的状态的能力。其下属二级指标包括接触网累计维修人时、平均故障修复时间、平均集中修维修天窗时间、累计临时修天窗时间和缺陷修复率。

1.2 接触网运行状态评价步骤

接触网运行状态的具体评价步骤如图2 所示。

图2 接触网运行状态评价步骤

采用min-max 归一化法对各项原始数据进行同质化转换，具体计算方法如式（1）所示。

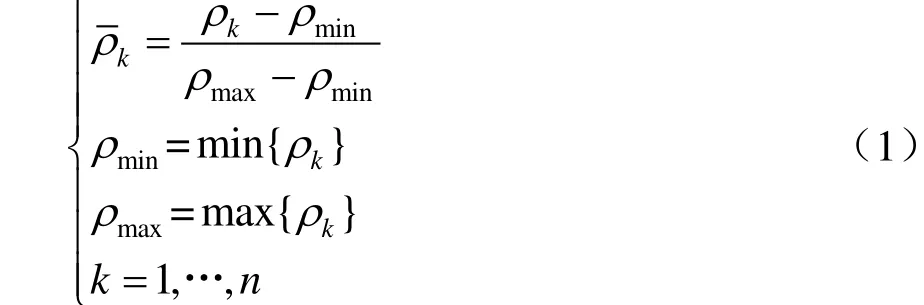
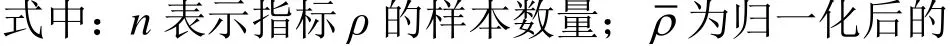
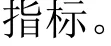
二级指标的权重由熵权法确定，即根据该指标的变异性的大小来分配权重[7]。一般来说，若某一指标的信息熵越小，表明该指标值变异程度越大，提供的信息量越多，在综合评价中所能起到的作用也越大，反之亦然。设m为该二级指标ρk的取值个数，T为该一级指标下的二级指标总数。定义ρk的信息熵为

式中：ρfir为一级指标，W为权重值，ρsec为二级指标。

令ρre、ρse、ρma分别表示可靠性指数、可用性指数和可维修性指数，α、β、γ分别为对应的权重系数，且α+β+γ=1。一级指标的权重采用专家法确定，则接触网系统的运行状态由式（6）计算：

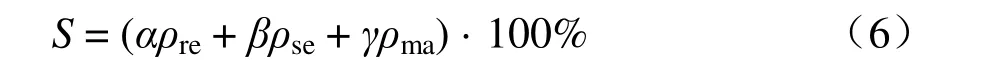
2 接触网状态退化过程

2.1 接触网系统状态退化模型

高速铁路接触网系统本身具有不对称结构，使得接触网系统受到频繁的负荷冲击，该类负荷具有典型的时间随机性和空间随机性，故相较一般电力系统，接触网系统中设备的衰退更为快速和显著。

Gamma 过程可以同时描述连续的微小冲击导致的缓慢变化和剧烈冲击引发的状态突变，这正是接触网运行状态的典型退化特征[8]。故本文采用Gamma 随机过程的方法对高速铁路接触网系统状态在实行检修维护等人工干预手段之前的退化过程进行建模，刻画该过程中时空随机性造成的影响。

设X(t)为接触网系统状态退化量，用于描述接触网系统状态在t时刻的衰退水平。则X(t)具有以下特征：（1）X(t)是一个单调递增变量，即在两次周期修作业期间，接触网系统退化量会随时间逐渐增加；（2）假设接触网系统周期修后状态与初始状态一致，则有X(0) = 0；（3）接触网系统在给定时间间隔Δt内，ΔX服从参数为a和b的Gamma 分布，即具有如下形式的概率密度函数：

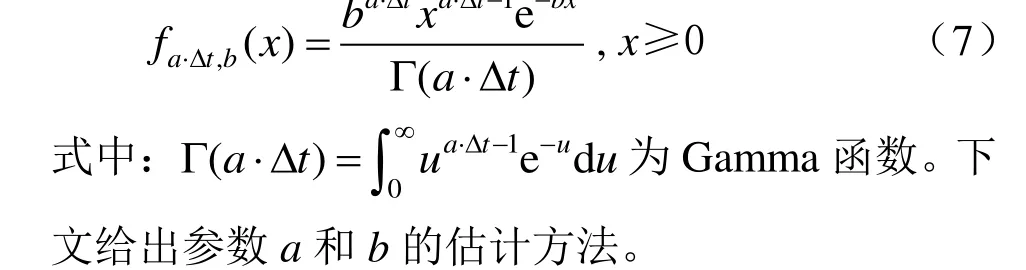
2.2 接触网系统状态退化模型参数估计

Gamma 函数的参数a和b被称为形状参数与尺度参数，具有明确的统计意义，即Gamma 过程的平均退化量（期望）为a/b，偏离平均退化量的不确定程度（方差）为1/b2。

在一个维修周期内每间隔两天计算一次接触网系统状态分值，得到接触网系统状态分值序列Sn。则接触网系统退化量序列计算式为

求解式（9），可得接触网系统状态退化过程参数。

3 接触网维修计划调整方案

3.1 主动维修策略

接触网系统主动维修决策过程是保持接触网系统具备良好运行状态的同时，将系统维护成本控制在较低的水平，进而达到系统运行状态和经济性的最佳平衡。假设连续两次周期修期间接触网系统的退化模式未发生显著改变，即相邻两次接触网维修周期的退化参数具有一致性。通过上一维修周期内接触网状态变化特征，预测本周期内接触网运行状态发展趋势，制定合理的临时修计划。

从系统安全性角度出发，高速铁路接触网系统大部分故障隐患是隐性的，出于成本和可靠性等方面的考虑，目前实际投入接触网系统运维的在线检测设备数量是有限的[2]，不利于发现接触网系统早期故障。但从接触网系统退化模型出发（图3），当退化量曲线X(t)出现峰值，表征接触网系统发生影响其运行状态的故障隐患，判定条件为

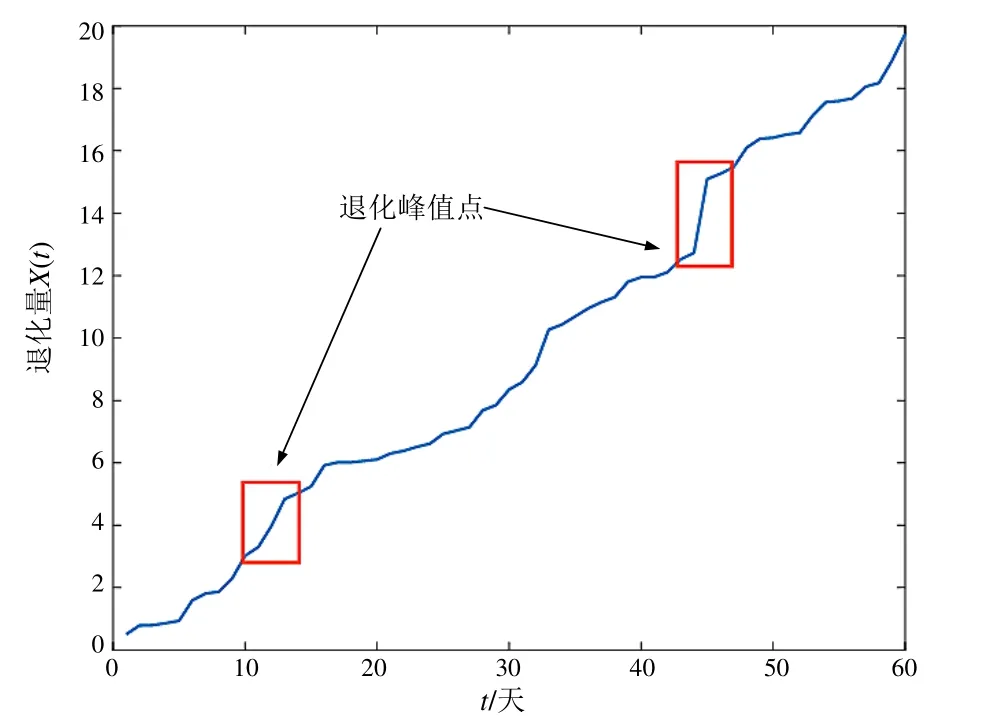
图3 接触网运行状态退化曲线

式中：η表示退化阈值，根据线路状况确定。

根据接触网系统运行状态评价模型，逆向查找引发运行状态得分下降的因素，并安排针对性的巡视检修计划。

另一方面，接触网系统维修策略的制定原则是在保障接触网系统安全可用的同时降低维护成本。为了对维修策略的性能进行定量评价，提出评价指标—性能退化成本率CR，其定义式为

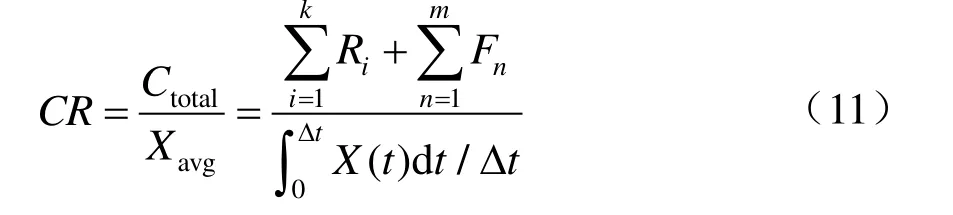
式中：Xavg为单个维修周期内接触网系统平均退化量，Ctotal为维修周期内合计维修成本，Ri为第i次临时修成本，Fn为第n次故障引发的损失。

性能退化成本率CR的物理意义是衡量铁路运营部门抵消接触网系统性能退化的影响所付出的成本。由于退化量和成本计算的复杂性，可采用蒙特卡洛方法求得接触网状态突变判定阈值与最优维修计划[9]。

3.2 计划修周期调整

高速铁路接触网系统的动态性能特征与整体性能的退化趋势具有一致性[10]。常用的傅里叶变换虽然能够准确提取信号的频谱，但无法将信号的频率与时间关联。当接触网动态检测参数出现异常时，往往需要分析其发生突变的时间，时频关系的确定则尤为重要。对接触网动态几何参数的时频特征进行分析，为掌握接触网运行状态提供了有效参考。

将接触网几何参数动态检测视为一个非平稳信号，采用Hilbert-Huang 变换可以提取其时频信息。具体步骤如下：

（1）采用经验模态分解（EMD）对该信号进行平稳化处理，自适应地将接触网几何参数动态检测信号Y(t)分解为多个窄带宽的内涵模态分量（IMF）[11]：

式中：ci(t)表示第i阶内涵模态分量；rn(t)表示残余分量。

（2）将EMD 分解得到的IMF分量进行Hilbert变换得到信号的瞬时频率及能量，对IMF 各个分量进行Hilbert 变换：

以时间为横坐标、频率为纵坐标建立平面坐标系，将幅度表示为瞬时频率和时间的函数，绘制的图谱即Hilbert 谱：

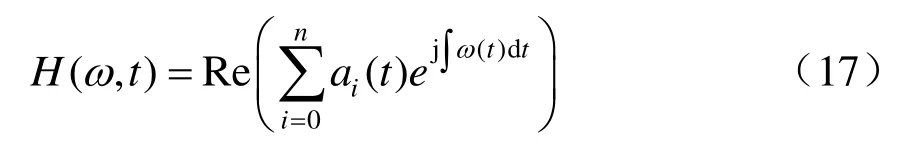
对单趟接触网动态检测数据的Hilbert 谱求和，可以得到当前接触网动态几何参数的能量和。当线路状态良好时，动态几何参数较为平顺，能量和小；线路状态退化时，动态几何参数波动剧烈，高频分量幅值增大，能量和较大。

如图4 所示，当能量和一旦超出临界值时，能量和呈陡增状态，经过维修处理后，接触网性能得到改善，能量和明显下降。

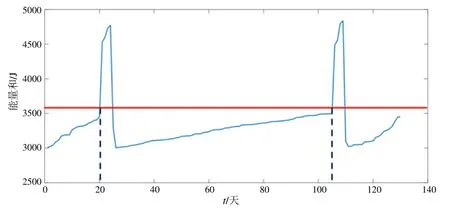
图4 接触网动态检测参数能量和趋势

对于某线路的检测数据，通过关联其历史数据，找到能量和变化临界值及变化周期，将计划修周期制定为两次超限值发生日期的时间间隔。

4 线路验证分析

4.1 接触网系统状态评价体系指标权重的计算

选取我国东部某高速铁路动车段7 区间8个站点在2021 年7 月—2021 年9 月的检修数据、动静态检测数据、缺陷记录、故障记录，验证本文提出的接触网系统状态体系的有效性。

根据专家法可得各一级指标权重向量为[α,β,γ]= [0.4,0.5,0.1]，计算各个一级指标下二级指标的熵值，得到各个二级指标权重如表1 所示。

表1 二级指标权重

4.2 确定接触网系统状态退化过程特征

计算2021 年第3 季度该线路接触网运行状态的趋势，每间隔2 天计算1次线路运行状态值序列，得到Sn= {99.9，99.4，95.7，94.9，94.0，93.3，91.2，88.8，87.0，86.8，85.0，84.6，84.6，83.7，81.9，81.6，81.5，81.0，80.5，79.8，79.4，78.6，78.4，77.5，77.2，76.8，75.6，72.5，71.4}。

绘制接触网系统状态值曲线如图5 所示。可以看出，接触网运行状态分值在单一维修周期内呈单调下降趋势，符合Gamma 过程的基本假设。

图5 接触网系统运行状态分值曲线

根据式（8）计算接触网系统退化值序列Xn，得到Xn={0.1，0.6，2.6，4.3，5.1，6.0，6.7，8.8，11.2，13.0，13.2，15.0，15.4，15.4，16.3，18.1，18.4，18.5，19.0，19.5，20.2，20.6，21.4，21.6，22.5，22.8，23.2，24.4，27.5，28.6}。进而求得退化序列的均值为15.33，方差为63.11，代入式（9）可求得接触网退化模型参数：a=121.78，b=7.94。

4.3 接触网系统主动维修计划建议

根据序列Xn计算线路接触网系统运行状态退化量的差分量并绘制其累计分布函数（CDF）如图6 所示。

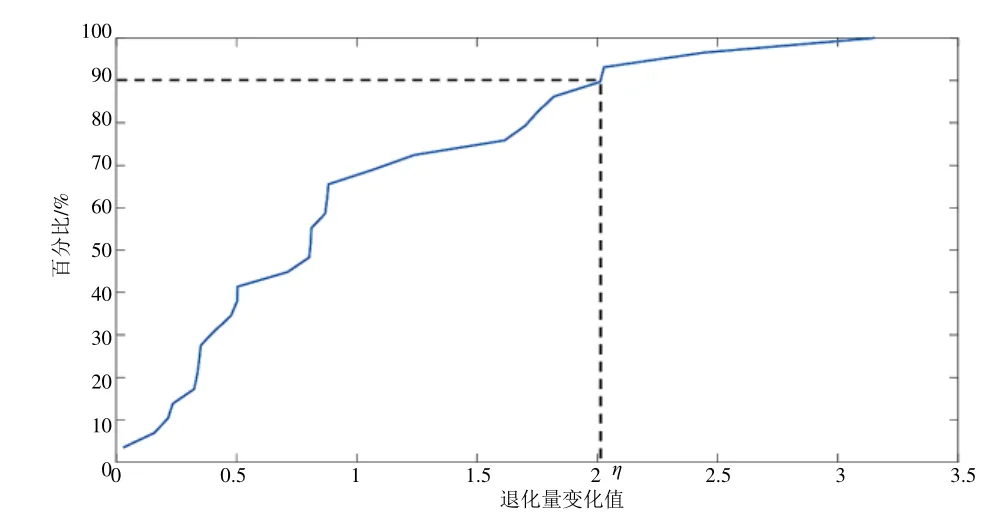
图6 接触网系统运行状态退化量变化值的累积分布函数

认为接触网系统在90%的时间处于低风险状态，10%概率出现故障隐患，即式（10）中触发临时修的阈值η对应为CDF 曲线值为0.9 时的退化量变化值，故η=2.02。

采用蒙特卡洛算法计算得到单次维修派遣人数和维修工时，如表2 所示。

表2 单次维修详情

该季度内临时修共计85 人·时，较2020 年3季度—2021 年2 季度的平均值(103 人·时)下降17.48%。且该季度内仅因雷击造成跳闸故障2 次，较2020 年3 季度—2021 年2 季度的平均值（3.7次）下降45.95%，大幅减少因线路故障引发的经济损失，按式（11）计算综合成本下降24%。由此，可证实所提主动维修策略的有效性，既能保证线路处于低故障风险，又可实现最低维修成本。

4.4 线路计划修周期建议

选取接触线高度为目标几何参量，每隔两天对线路动态接触线高度检测结果进行抽样，选取5 条动态检测数据文件分别进行HHT 分解，计算其能量和的均值作为当日线路能量和。2021 年第3 季度内线路动态接触线高度能量和趋势见图7。

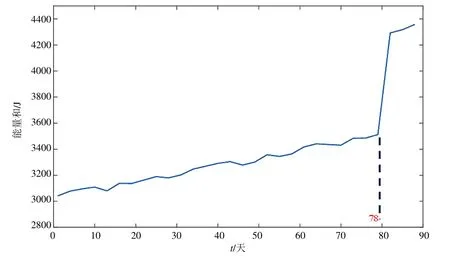
图7 动态接触线高度能量和趋势

从图中可以得出以下结论：

（1）动态接触线高度能量和在一个维修周期内总体呈上升趋势，但受到检测设备误差与外部环境因素的影响，导致部分时间点接触线高度能量和出现振荡。

（2）本季度第78 天能量和为3 512 J，此后能量和剧增，可以推断动态接触线高度能量和临界值约3 500 J，建议调整计划修周期缩短至80 天。

（3）第81 天能量和剧增时，接触网系统运行状态出现退化峰值点，映证两者对接触网系统运行状态的刻画具有一致性。

5 结语

本文综合考量影响接触网运行状态的因素，建立高速铁路接触网系统运行状态评价体系，推导基于Gamma 过程的接触网系统状态退化模型。在此基础上结合HHT 时频分析方法提出主动维修建议和最佳接触网维修周期。结合某高铁实际运营数据表明：接触网状态评价体系与退化模型可准确全面地描述接触网状态发展趋势；主动维修策略和维修周期建议在消除接触网系统故障隐患的同时能更合理地统筹维修资源，综合维修成本下降约24%。综上，本文所述方案切合接触网系统运营需求，具有一定的实际应用价值。