无先验模型复杂结构设施SAR全方位三维成像方法研究

林 赟 张 琳 韦立登 张汉卿 冯珊珊 王彦平 洪 文*

①(北方工业大学信息学院雷达监测技术实验室 北京 100144)

②(北京无线电测量研究所 北京 100854)

③(中国科学院空天信息创新研究院 北京 100094)

④(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)

1 引言

合成孔径雷达(Synthetic Aperture Radar,SAR)具有全天时全天候高分辨成像能力，是对地观测的重要技术手段之一。目前，基于常规SAR图像的判读解译主要有两方面难点：(1)图像为二维图像。存在叠掩、遮蔽、顶底倒置和透视伸缩等几何形变现象，难以准确反映目标真实的三维结构。在复杂环境下，因叠掩等现象会造成目标看不清、辨不明。(2)图像特征对观测角度极为敏感。目标的微波散射特性对角度敏感，导致SAR图像特征受观测角度影响大，获取的目标信息不完整。

圆迹SAR将常规SAR的观测维度拓展到了角度维，角度这一新观测维度的引入使得获取得到的目标信息显著丰富。首先，圆迹SAR具有解叠掩能力，因数据获取的距离-方位斜距平面随观测角度变化，在某个方位角度叠掩的两个目标，在另一个方位角度不再叠掩，即圆迹SAR信号包含了目标的三维结构信息。此外，圆迹SAR利用不同角度的散射信息互补可得到更完整的目标散射特性。因此，圆迹SAR全方位三维成像可有效解决判读解译应用中图像的叠掩和角度敏感性等问题，在不增加系统复杂度的条件下能够丰富SAR对目标精细特征的获取能力[1-6]。

圆迹SAR的信号频谱近似为圆台曲面，理论上三维分辨率很高。然而，由于信号频谱为稀疏曲面谱，三维点扩展函数旁瓣高，且实际数据获取中，目标散射特性随角度变化，因此难以采用常规三维成像方法获得理想的三维图像。现有圆迹SAR三维成像方法主要有以下几种方式。

(1) 借助高程向多通道或多条重复轨迹的三维成像方法。多通道或多条重复轨迹圆迹SAR是在高度向形成近似均匀分布的多个圆周轨迹，对目标进行凝视观测。该方法通过高程向合成孔径，并利用目标的稀疏特性，实现高程向的超分辨[7,8]。

美国空军实验室在2006年公开了多基线圆迹SAR数据集[9]，数据由8条全极化轨迹构成，目标包括各种类型的民用车辆。此数据的公开为圆迹SAR三维成像的研究提供了有利条件。国内外众多研究学者利用该数据开展研究，获得了较为理想的结果[10-13]。

德宇航从2015年开始对建筑区、林区、冰层区、农业区进行了多航迹圆迹SAR三维成像[14-16]，获得了建筑、树木、冰层、作物的垂直结构。基线数量和跨度直接决定了垂直结构的精细度，文献[16]的实验中采用了19条全极化数据。该文采用基于压缩感知的超分辨方法获得了较为理想的结果。

无论是多通道还是多轨迹三维成像，现有方法中高程向超分辨与圆迹成像独立进行，多方位角数据本身的三维成像能力未加以利用。多轨迹圆迹SAR对基线的数量、长度和均匀性等都具有较高要求，数据获取难，无法满足时效性要求；多通道系统的通道数量和基线跨度受限于平台，现有方法需借助辅助信息来改善模糊和低分辨率问题[17]。

(2) 借助阴影信息或目标先验模型的圆迹SAR三维成像方法。方法主要针对结构较为简单的目标开展，如车辆、简单结构建筑、高塔等[18-22]。

在阴影信息利用方面，文献[20]对结构较为简单的高塔类建筑，提取各角度阴影，根据射线原理解算目标的三维结构。

在目标先验模型利用方面，文献[18]利用圆迹SAR图像中简单建筑4个方向二面角散射的闭合性，提取建筑物所处地面的高度信息。文献[19]利用输电线仅在相差180°的两个方向可见的特性，提取输电线高度。文献[21]利用普通车辆在圆迹SAR图像中形成的内外双环特征，提取车辆顶层高度信息。

上述目标先验信息的利用降低了圆迹SAR三维成像对多通道或多条重复轨迹的要求，但目前先验信息的利用还较为简单，需要针对特定目标建立特定先验模型，仅适用于简单结构目标，难以用于复杂结构目标的三维成像。

中国科学院空天信息创新研究院微波成像新概念新体制新技术研究团队提出了多角度SAR的概念，在国家自然科学基金项目、国家预研等项目的支持下，持续开展以圆迹SAR为代表的多角度SAR成像技术研究[1,2,23-29]，在多角度SAR三维成像机理及方法等方面具有长期的研究积累和技术成果[5,10,18,19,30-37]。此次，中国科学院空天信息创新研究院、北方工业大学和北京无线电测量研究所联合开展圆迹SAR三维成像机载实验，数据由北京无线电测量研究所研制的Ka波段机载干涉SAR系统获取，首次成功获得国际首幅500米口径球面射电望远镜(Five-hundred-meter Aperture Spherical radio Telescope,FAST)全方位三维图像，为复杂结构重要设施的精细三维结构信息获取提供了技术支撑。

本文以FAST全方位三维成像实验采用的干涉圆迹SAR (Interferometric Circular SAR,InCSAR)模式为例，首先介绍了无先验模型复杂结构设施SAR全方位三维成像方法的基本原理。本方法综合了干涉测量的高精度测高能力和圆迹SAR的全方位观测、解叠掩和解高程模糊优势，利用圆迹SAR多方位角数据本身的三维信息获取能力解决干涉相位模糊带来的目标高程模糊问题，一次飞行获取全场景全方位三维图像。本方法无需目标预先建模和三维成像网格构建，适用于大场景复杂结构设施的三维精细成像。然后，本文给出了实验实施情况以及数据处理结果，验证了理论和方法的正确性、有效性；最后总结全文，并对未来研究进行了展望。

2 干涉圆迹SAR几何模型与信号模型

2.1 几何模型

干涉圆迹SAR的几何模型如图1所示，雷达平台包含两个跨航向天线相位中心：天线相位中心1和天线相位中心2，分别记为T1和T2。两个天线相位中心的连线(称为基线)与雷达平台航迹方向垂直，基线长度为B，其与水平面的夹角为β。雷达平台围绕感兴趣区域作360°圆轨迹运动，波束始终指向同一区域，θ为方位角，H为雷达平台飞行高度，r为天线相位中心1的轨迹半径。圆轨迹可以是非标准圆，对于非标准圆轨迹，β,θ,H,r等参数均指数据采集时刻的瞬时参数。

图1 干涉圆迹SAR观测几何Fig.1 InCSAR imaging geometry

2.2 信号模型

以线性调频信号体制为例，天线发射信号为

其中，函数 r ect()表 示矩形波，t为快时间，fc为工作频率，k为调频率，Tp为线性调频信号脉冲长度。假设P为观测场景中的任意点目标，如图1所示，则P的回波信号经正交解调后的基带信号为

其中，下标i为天线相位中心序号，σp为目标散射系数，c为光速，Rp,i为目标距离天线相位中心的距离，其表达式为

其中，(Xi,Yi,Zi)为 天线相位中心的三维坐标，(xp,yp,zp)为点目标P的三维坐标。

对式(2)作快时间傅里叶变换，变换至距离频域，信号表达式为

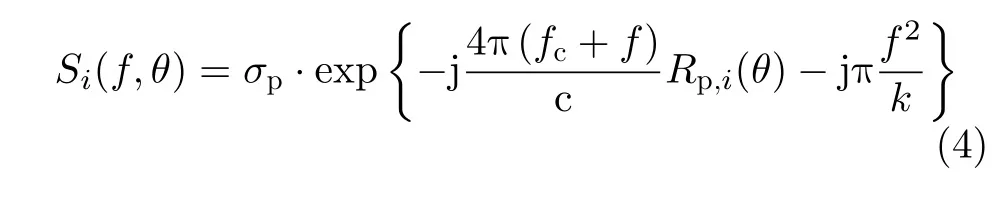
其中，f为快时间t对应的频率。将式(4)与频域匹配滤波器相乘完成距离压缩，频域匹配滤波器的表达式为

令波数Kr=4π(f+fc)/c，则匹配滤波后，距离频域信号表达式为

3 无先验模型全方位三维成像方法

3.1 基本原理

圆迹SAR数据获取时，因距离-方位斜距面随观测角度变化，在某个方位角叠掩的两个目标，在另一个方位角不叠掩，因此圆迹SAR本身就具有三维成像能力。如图2所示，在观测角度θ1，点目标P1与 P2的等距离等多普勒线重叠(在图中以红线表示，等距离等多普勒线垂直于斜距面)，则两点目标在该角度叠掩；在观测角度2，点目标 P1的等距离等多普勒线以蓝色表示，点目标 P2等距离等多普勒线以黄色表示，两线不重叠，即两点目标在该角度不叠掩。

图2 圆迹SAR解叠掩能力示意图Fig.2 Layover resolving capability of circular SAR

然而，由于圆迹SAR信号频谱为圆台曲面，频谱稀疏，点扩展函数的旁瓣很高。此外，在全方位观测条件下目标散射非各向同性。因此，采用传统相干累积的三维成像方法难以获得复杂结构目标的三维图像。

SAR干涉测量能够通过干涉相位反演目标高精度高程，然而相位被 2π缠绕，存在相位模糊问题。在地形连续区域，可利用干涉相位的连续性，采用相位解缠的方式解决相位模糊问题，反演高精度地形。然而对于复杂结构目标，如建筑等，干涉相位不连续，难以通过相位解缠来确定绝对相位。因此，目前干涉SAR主要用于地形反演，未见用于目标的三维结构重建。

干涉圆迹SAR结合了干涉SAR的高精度测高能力和圆迹SAR的全方位观测、解叠掩优势。本文提出利用圆迹SAR多方位角数据的三维信息获取能力解决干涉相位模糊带来的高程模糊问题，能够对复杂结构目标进行精细三维成像。如图3所示，干涉圆迹SAR解模糊三维成像的主要流程如下。

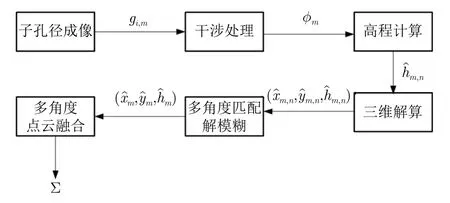
图3 无先验模型SAR全方位三维成像方法流程图Fig.3 Flow chart of full-aspect 3D SAR imaging method without prior model

(1) 子孔径成像。首先将圆迹SAR数据划分为若干个子孔径数据，各子孔径数据在统一坐标系oxyz的固定高程平面成像，可采用后向投影算法得到精确的子孔径图像，子孔径图像的表达式为

其中，m为子孔径序号，h0为 成像平面高程，(x,y)为成像平面像素坐标，Δθ为子孔径角度大小，Kmin和Kmax分别为波数Kr的最小值和最大值，Ri(θ,x,y,h0) 为天线相位中心到坐标(x,y,h0)的距离。子孔径角度大小可按分辨率需求设定。

(2) 干涉处理。对应子孔径序号，不同天线获取的两幅图像无需配准，直接做干涉处理，计算干涉相位。干涉相位的表达式为

其中，函数a rg()代 表求相位，符号*代表共轭。

(3) 高程计算。利用干涉相位计算各像素的高程信息，因相位模糊，高程信息也存在模糊，得到N种可能的高程，记为n为整数，代表模糊数。N的选取与目标高度范围及不模糊高度有关，假设目标高度范围为hr，不模糊高度为hua，则

其中，符号「表示不小于符号内数值的最小整数，不模糊高度hua的表达式将在第3.2小节中给出。

(4) 三维解算。基于距离多普勒方程解算各像素的三维坐标，记为，由此得到存在高程模糊的三维点云。

(5) 多角度匹配解模糊。根据N种高程假设对多角度图像进行匹配，根据最优匹配，在N种模糊点云中确定解模糊的三维点云

下面将对干涉相位推导、三维解算和多角度匹配解模糊这3个主要研究内容进行详细阐述。算法推导中的参数均采用数据采集时刻瞬时观测参数，如天线相位中心瞬时位置、相对于目标的瞬时视角等，未采用标准圆轨迹、场景中心目标假设，适用于非标准圆轨迹SAR大场景三维成像。

3.2 干涉相位推导

干涉圆迹SAR在任意观测角度的瞬时观测几何如图4所示。为表述方便，建立新坐标系o′x′y′z′。该坐标系以平台速度矢量方向为y′方向，垂直向上方向为z′方向，根据右手坐标系准则确定x′方向。T1和T2分别代表2个天线相位中心的位置。Q1和Q2分别为点目标P在该角度两幅子孔径图像中的聚焦投影位置，位于零多普勒面，位置由SAR的距离-零多普勒成像原理决定，且|T1P|=|T1Q1|,|T2P|=|T2Q2|，图中蓝色和绿色弧线分别代表T1和T2到点目标P的等距离等多普勒线。角度α为目标相对于天线的入射角，角度ψ为目标斜视角。

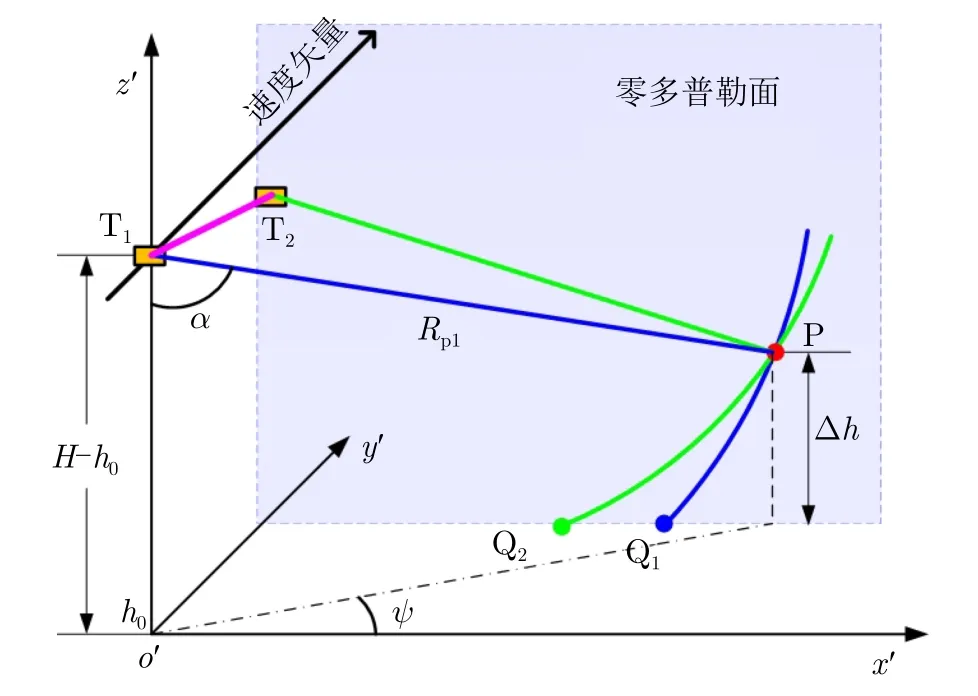
图4 干涉圆迹SAR瞬时观测几何Fig.4 Instantaneous geometry of InCAR

由于两个天线相位中心的入射角存在差异，当目标高程与成像平面高程不同时，两幅干涉图像存在偏移，从而产生干涉相位。

点目标P与参考平面的高程差 Δh的表达式为

两天线相位中心到点目标的距离差 ΔR的表达式为

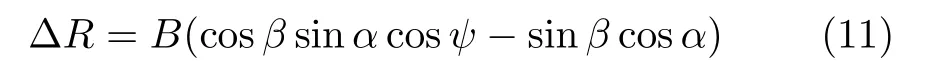
本文两幅用于干涉的图像在统一地平面坐标系成像，因此无需配准，且干涉相位中不包含平地相位，则干涉相位与目标高程呈近似线性关系，即

其中，ϕ为缠绕干涉相位，n为模糊数，Kc为中心波数。根据式(12)，目标的高程表达式为

式中的高程信息存在模糊。相邻模糊数对应的高度差为不模糊高度，其表达式为

3.3 三维解算

基于距离多普勒方程的三维位置精确解算依赖于天线相位中心位置、姿态等参数的高精度测量，将在后续研究中进一步定量分析各测量参数误差对三维点云精度的影响，本文不做讨论。

3.4 多角度匹配解模糊

利用多角度观测的子孔径图像偏移特性可以解决干涉相位模糊带来的高程模糊问题。如图5所示，Qm为第m幅子孔径图像的任意像素，坐标为(x,y)，通过干涉相位计算得到了该像素N种可能的高程，需要在这些估计值中选择最接近真实值的高程估计。图5中，假设红色点P为其真实三维位置，红色弧线是观测角度为θm时的等距离等多普勒线，蓝色点代表N种高程估计，蓝色点位于红色弧线上。根据这N种高程假设，通过距离-等多普勒投影原理，可以得到该像素在第m+J幅子图像中的投影位置，记为Qm+J,n，坐标为(xm+J,n,ym+J,n)，图5投影位置以黑色点表示，蓝色弧线为N种三维位置假设在观测角度θm+J的等距离等多普勒线。

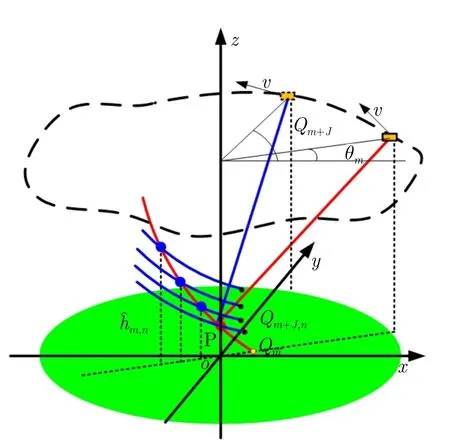
图5 多角度解模糊示意图Fig.5 Diagram of multi-aspect ambiguity resolving

投影位置Qm+J,n与Qm的偏移距离近似与高程估计值成正比：

第m幅子孔径图像在点Qm的 邻域与第m+J幅子图像在点Qm+J的邻域应具有相似的图像特征。因此，N种投影点Qm+J,n中，邻域与Qm邻域匹配度是最高的，对应的模糊数n即为真实模糊数。

多角度匹配解模糊流程图如图6所示，具体如下。

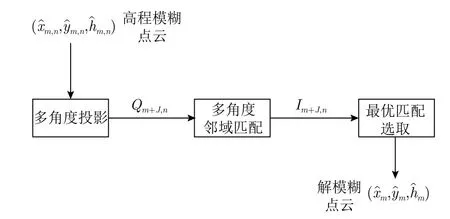
图6 多角度匹配解模糊流程Fig.6 Flow chart of multi-aspect ambiguity resolving

其中，Gm为第m幅子孔径图像Qm邻域幅度图，Gm+J,n为 第m+J幅子孔径图像Qm+J,n邻域幅度图，符号C ov表 示求互相关，V ar表示求方差。

(3) 最优匹配选取。选取相关系数最大值对应的模糊数n，获得解模糊的三维点云。表达式为

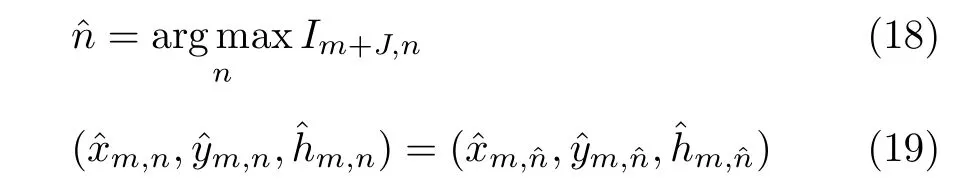
多角度匹配解模糊中，孔径间隔J的选取需要考虑解模糊能力和图像特征的相似性。解模糊能力可根据式(16)进行计算，当不模糊高程hua引起的多角度图像偏移越大，解模糊能力越强；但同时为了保证多角度图像具有相似的图像特征，孔径间隔J又不能取得过大。

4 实验验证

实验数据由北京无线电测量研究所研制的Ka波段机载干涉SAR系统获取。该系统采用固态有源天线体制，在单个吊舱内集成多部收、发天线，单次飞行获取的多通道数据可组合成单基线干涉、多基线干涉、多极化成像、多极化干涉等多种业务模式。其吊舱具备两轴伺服调节功能，并集成了高精度位置和姿态测量设备，为复杂曲线轨迹数据获取提供了精确的天线姿态和位置信息。

机载实验观测目标FAST位于中国贵州省内，是世界最大的球面射电望远镜。圆迹飞行轨迹的中心设计为FAST球面镜中心，飞行半径约为3000 m。FAST主要组成部分包括500 m口径球面反射面、馈源支撑塔(6座)、球面反射面支撑格构柱(50根)等。实验主要参数如表1所示，飞行轨迹与FAST光学照片如图7所示。

图7 机载实验飞行轨迹与观测目标Fig.7 Flight trajectory and the observed object

在本实验中，子孔径角度大小为1°，根据表1参数，子孔径图像地距分辨率和方位分辨率均约为0.25 m。某子孔径SAR图像与干涉相位图如图8所示。FAST结构复杂，馈源支撑塔、支撑格构柱等为垂直结构，相位变化梯度大，且主要图像特征为点状强散射，相位不连续，难以通过相位解缠解决干涉相位模糊问题。FAST球面反射面结构的散射特性复杂，多径效应明显，给三维成像带来困难。

图8 某子孔径SAR图像与干涉相位图Fig.8 SAR image and interferogram of certain subapture

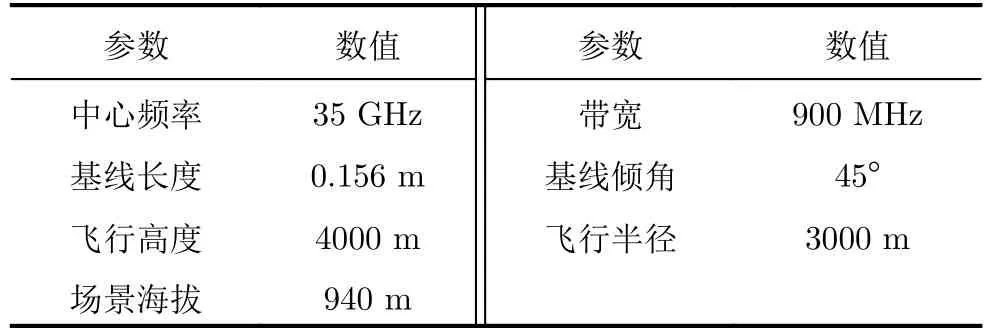
表1 Ka波段机载干涉圆迹SAR实验参数Tab.1 Parameters of Ka-band airborne InCSAR experiment

图9(a)为根据干涉相位进行高程反演和三维解算后的某角度局部目标三维点云，因相位缠绕，该三维点云存在高程模糊，即模糊数不确定，目标的高程信息有多种可能。图9(b)为采用多角度解模糊后的三维点云。多角度解模糊利用多角度图像的偏移特性，通过多角度匹配来确定模糊数，解决高程模糊问题，无需采用基于相位连续性假设的相位解缠操作，为相位解模糊提供了新的思路。在本实验中，多角度去模糊的孔径间隔取值为5，即两幅图像的角度差为5°，根据该参数，并将式(14)代入式(16)，可得不模糊高程带来的图像偏差约为7 m，利于多角度匹配去模糊。因子孔径角度较小，仅为1°，目标信息获取不完整，还需要对多角度点云进行融合获得全方位信息。

图9 某子孔径三维点云Fig.9 3D point cloud of certain subapture

图10为全方位三维图像与常规条带SAR图像的对比。如图10(a)所示，受限于雷达观测几何及二维成像方法，常规SAR图像存在阴影、叠掩、透视伸缩等现象，部分目标结构不可见。图10(b)-图10(d)从不同视角展示了全场景、全方位三维图像，视角方向如图7(b)中示意，展示图的下视角为35°，3个视角的方位角间隔90°。图10中，FAST三维立体结构清晰可见，红圈内为悬挂于球面反射面之上的馈源。馈源支撑塔高度测量值约为168 m(颜色表对应散射中心海拔高度)，与实际情况相符，后续将进一步开展定量化精度分析研究。需要说明的是，因球面反射面散射特性复杂，多径效应明显，本文未对球面反射面进行三维成像，将在后续进一步开展研究。

图10 常规条带SAR图像与全方位三维SAR图像对比Fig.10 Comparison between conventional stripmap SAR image and full-aspect 3D SAR image

5 结语

本文提出了无先验模型SAR全方位三维成像方法，结合干涉SAR的高精度测高优势和圆迹SAR全方位观测、解叠掩和解高程模糊优势，实现复杂结构目标三维成像。该方法挖掘多方位角数据的三维成像能力，无需目标预先建模和三维成像网格构建，一次飞行即可获得先验信息未知区域全场景全方位三维图像，适用于复杂结构设施的精细三维结构获取，在雷达三维成像实用化技术方面取得了重要进展。

联合团队将进一步深入开展相关研究工作，挖掘多角度等新观测维度带来的信息增量，围绕三维散射特征描述方法，探索新型、高效数据获取模式及处理方法，进一步推动复杂场景多维信息精细化描述的实际应用。