桥梁形变监测中LSTM 预测方法研究

杨国林，孙学先，锁旭宏，刘 涛，曹 辰

（1.兰州交通大学测绘与地理信息学院，兰州 730070；2.兰州交通大学地理国情监测技术应用国家地方联合工程研究中心，兰州 730070；3.中交一航局第二工程有限公司，山东青岛 266071；4.兰州交通大学甘肃省地理国情监测工程实验室，兰州 730070）

各种不同类型的神经网络方法对人工智能和机 器学习有新的促进，它们都在各自应用领域有着重要意义［1-3］.其中在标准的循环神经网络（recurrent neural network，RNN）中，神经元之间存在反馈和前馈连接，动态处理和计算能力比传统的前馈神经网络更加出色，在时序数据处理中表现出很强的适应性［4-5］.在 RNN网络基础上发展来的长短期记忆（long short-term memory，LSTM）神经网络有了新的改进［6］，其主要优点体现在：RNN在样本训练过程中，由于训练的时间积累过多，从而导致网络层数的改变越发频繁，就可能产生梯度爆炸，形成梯度消失问题［7-8］，无法获得长程信息.新的方法能在这些方面有针对性改进，LSTM当前已成功应用的领域包括文本生成、机器翻译、语音识别、生成图像描述和视频标记等［9-11］.当前针对桥梁形变预测方法主要包括灰色理论法，时间序列模型、回归模型等预测模型法，主要能进行短期预测，LSTM方法可弥补这一不足，在构筑物变形监测数据处理方面，相较常规方法具有优势.

在建设工程中桥梁沉降及倾斜变形监测十分重要，通过准确地预测桥梁工程建设中沉降和倾斜的变化过程，就能较早地找到桥梁形变的异常状况从而进行必要的应对调整，防止灾害出现造成工程损失［12-14］.

通过利用桥梁实测数据对建立的RNN和LSTM网络模型分别进行训练及预测，在RNN网络基础上根据Martin等［15］改进的LSTM网络能够学习时间序列中的短期和长期相关信息，克服了RNN相关的问题，结果表明，LSTM网络能够对观测数据进行高精度和稳定的拟合和预测，能够有效地描述桥梁的变形规律.

1 RNN和LSTM 原理介绍

1．1 RNN循环神经网络

RNN的模型结构图中涉及到输入、输出和中间的隐藏层，在当前时间隐藏层中有连接输入到下一时间隐藏层．对于给定序列 x=（x1，x2，…，xn），可以通过迭代式（1）和式（2）计算出一个隐藏层序列h=（h1，h2，…，hn）和一个输出序列 o=（o1，o2，…，o2）．结构如图1所示．

图1 RNN模型细胞结构Fig．1 Cell structure of RNN model

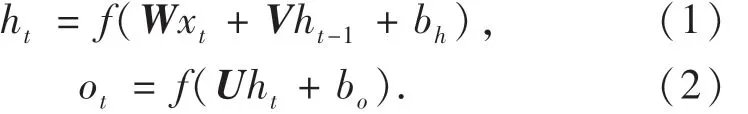
式中：W为给定序列的权重系数矩阵；U为隐藏序列的权重系数矩阵；V为输出序列的权重系数矩阵；b为偏置向量；f为激活函数．

过程中普遍采用的（3）和（4）式的sigmoid激活函数和tan h激活函数．在特征信息相差比较大的情况通常使用激活函数tan h；在相差较小时使用函数sigmoid，同时对输入数据进行规范化处理．

1．2 LSTM 长短期记忆网络

LSTM网络中有时间记忆单元，LSTM网络是将RNN隐藏层的细胞替换为LSTM细胞，即具有了长期记忆的特性，LSTM模型细胞结构如图2所示.对于学习时间序列依赖于时期长短的问题与长序列建模问题，可以更好处理存在于RNN中的问题，改进效果明显［16-17］.

图2 LSTM 模型细胞结构Fig．2 Cell structure of LSTM model

其中LSTM在t时刻输入的序列值为xt，输出值及控制单元状态为ht-1和ct-1；LSTM的输出为：输出值ht及控制单元状态ct.计算分别见式（5）～（7）［18］：

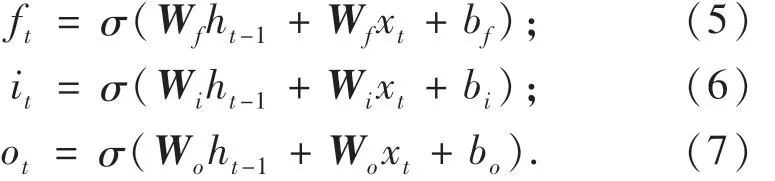
式中：Wf、Wi、Wo为权重矩阵；bf、bi、bo为偏置项［19］．

具体开展研究的方法流程如图3所示.

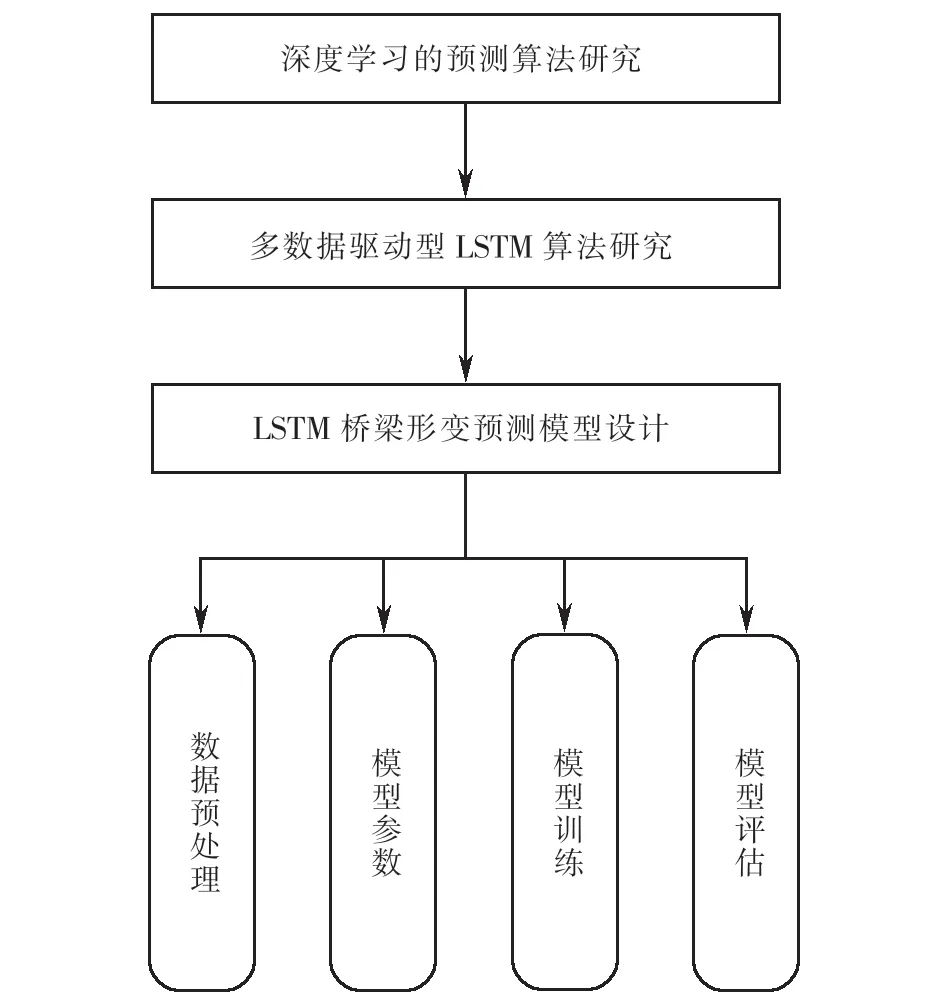
图3 数据处理流程Fig．3 Flowchart of Data processing

首先开展深度学习预测算法的归纳分析，然后进行多数据驱动型LSTM算法研究，特别针对桥梁形变进行LSTM预测模型设计，具体通过数据的预处理、模型参数的计算、进行样本的模型训练和对模型进行评估，实现LSTM算法对桥梁形变的预测分析.

2 实例分析

2.1 实例研究过程

使用基于Sequential-Keras模型所构建的基于单元素分析的三层神经网络框架，拟定输入输出单元，过程中单元误差函数为标准差，激活函数为adam.现用一桥梁的长周期形变观测数据对其进行训练和预测，数据如表1所列.通过差分使数据稳定，并将数据转换为有监督数据，对转换后的数据进行拆分，分为训练数据和测试数据并进行缩放.通过确定步长、迭代次数和神经元数量参数进行训练和预测，并根据RMSE的值调整参数直至参数满足精度要求.

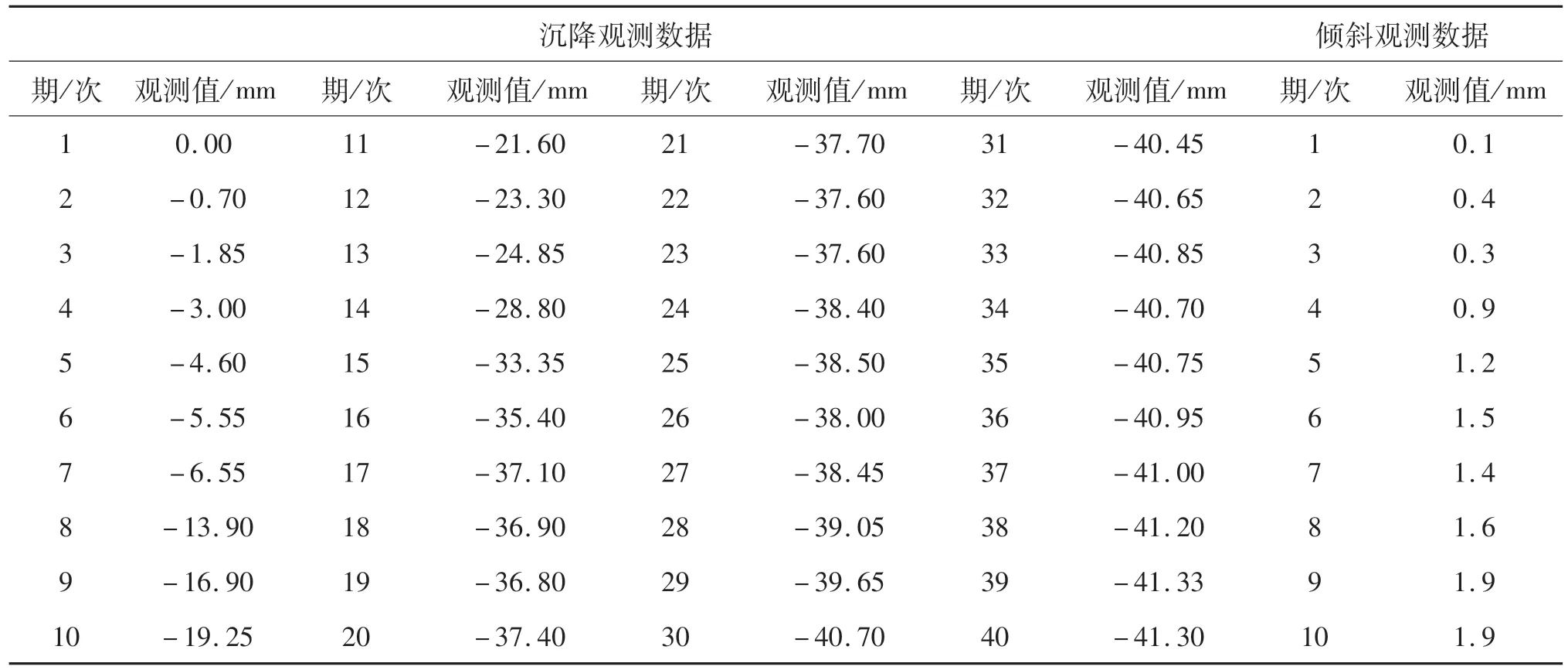
表1 桥梁观测数据Tab．1 Bridge measured data

2.2 数据结果分析

研究方案中以前35期沉降观测数据作为训练样本，后5期数据作为测试样本，经过相应程序计算，该桥梁的沉降曲线如图4所示，两种方法分别开展沉降预测，成果分析如图5所示，倾斜曲线如图6所示.另外以前7期倾斜方面观测的数据作为样本，以后面3期倾斜观测数据作为测试样本，经过相应程序进行倾斜预测，其成果对比如图7所示，结果对比及分析如表2～3所列.

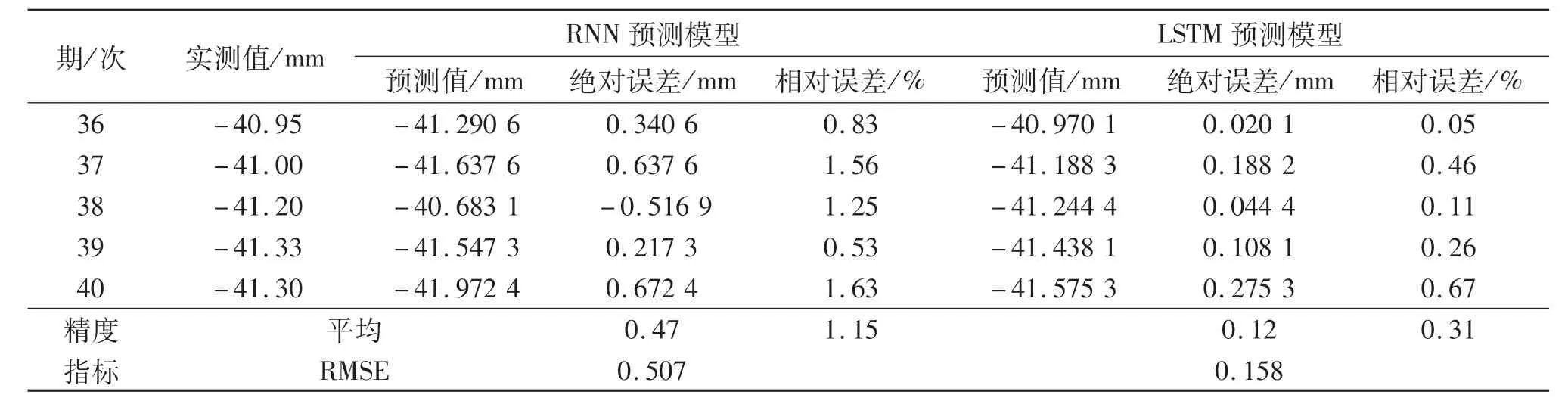
表2 沉降观测值与预测值比较Tab．2 Comparison of settlement measured and predicted values

图5 沉降预测结果对比Fig．5 Comparison of settlement prediction results

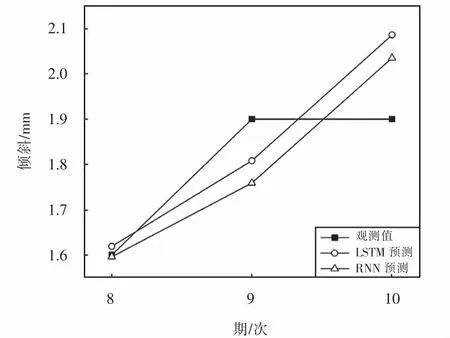
图7 曲线预测结果对比Fig．7 Comparison of tilt prediction results

分析图4表明，桥梁的沉降在第1期至第6期时间段内经历一个缓慢下沉过程，此时处于施工期，随后在第6期至第17期时间段内快速下沉，之后下沉速率放缓并趋于稳定.分析图6，受施工因素、地质条件和自然天气等对桥梁的下沉及倾斜造成的综合影响，表明桥梁的倾斜具有一定阶段性.

图4 沉降曲线Fig．4 Settlement curve of bridge

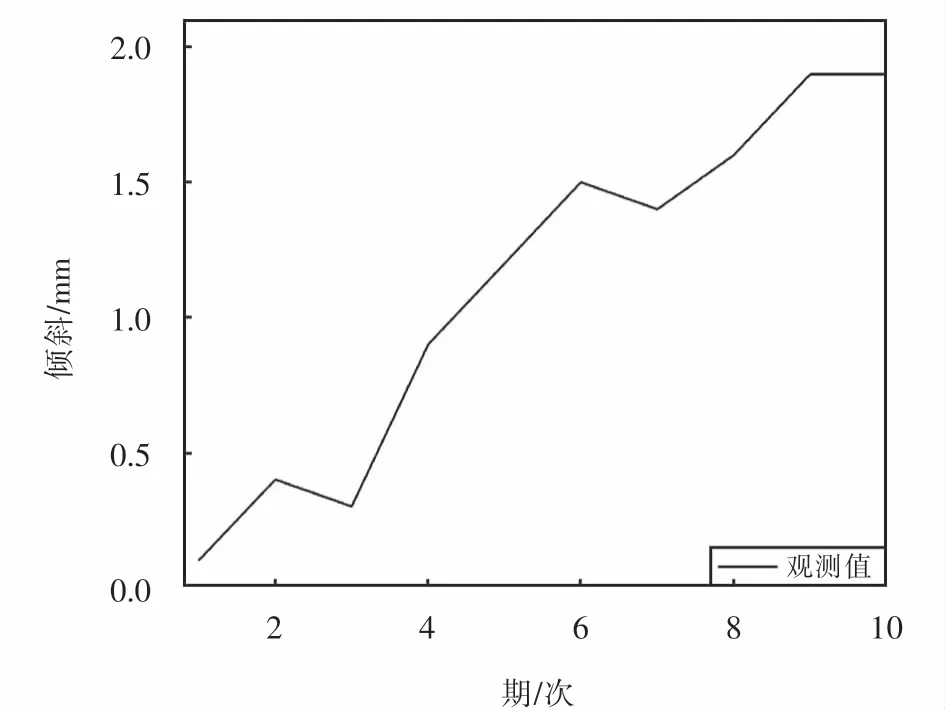
图6 倾斜曲线Fig．6 Tilt deformation curve of bridge

分析图5和图7表明，采用训练样本对LSTM进行训练的效果要好于RNN，RNN训练误差离散较大，LSTM在各个测试样本误差都较小.对于桥梁倾斜的预测，LSTM和RNN最终结果接近，在一定的时间序列处理中LSTM的提升不显著.大量的重复训练试验表明通过增加迭代次数、隐藏层层数和神经元个数使RNN预测精度的提高效果不大，而在同种试验条件下LSTM预测精度都较高，尤其是在长序列预测中.

统计所有过程数据并根据表2相关信息表明，RNN预测平均绝对误差为0.47 mm，平均相对误差为1.15%，标准差为0.507.LSTM方法得到的平均绝对误差值是0.12 mm，平均相对误差是0.31%，标准差为0.158.LSTM较RNN预测精度有整体提升，能较准确反映桥梁的沉降规律.从表3可以看到，RMSE值分别为0.120和0.113，二者在倾斜短时间序列预测中效果接近.RNN存在梯度消散问题，在特定实际情况下建模效果较差.在RNN基础上改进的LSTM较好地解决了这个问题，考虑到当前信息对过往信息的影响，增加不同长短时期信息的学习，对时间序列遇到间隔与延迟的情况下更为可靠.

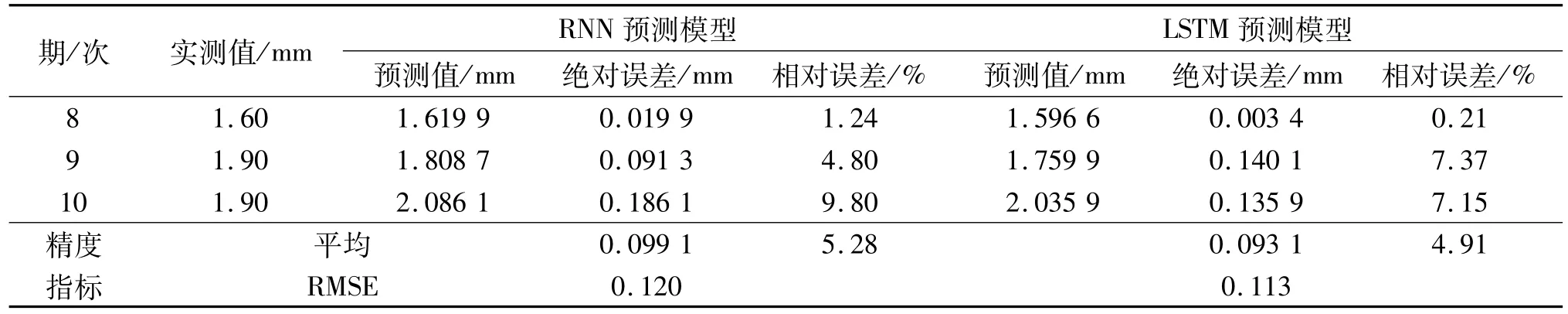
表3 倾斜观测值与预测值比较Tab．3 Comparison of tilt measured and predicted values

3 结论

工程施工监测更加自动智能的条件下，预测质量的提高对形变监测关系重大.利用桥梁的实测数据对RNN和LSTM网络开展训练和预测，由研究结果可知，在对桥梁的沉降与倾斜的监测中，两者都能反映桥梁的沉降规律，在倾斜短时间序列预测中效果接近，同时LSTM能更好解决梯度消散问题，且LSTM网络性能更稳定、更准确，效果明显优于RNN网络，对桥梁形变的预测和分析更具优势.因此应用LSTM在桥梁变形预测中有较好的适用性，能为类似形变监测提供参考依据.