FeGa/PZT圆柱体磁电复合材料在8/20 μs雷电激励下磁电响应仿真分析*

李 跃,肖小兵,蔡永翔,张紫嫣,鲁彩江

(1. 贵州电网有限责任公司电力科学研究院， 贵阳 550005；2. 西南交通大学 机械工程学院， 成都 610031)

0 引 言

雷电测量在雷电防护技术中至关重要，是雷电研究的基础。因此，在新型电力系统建设背景下，要防止和减少电网事故，就要准确获知雷电流大小以及波形，在此基础上结合相关风险评估系统，构建电网全方位预警评估系统，其中蕴含着显著的学术价值、巨大的社会和经济效益，实现这一切不可或缺的工具就是瞬态磁场传感器。

在瞬态电流测量领域，最常用的是罗氏线圈[1-3]和光学传感器[4]。Rogowski线圈克服了磁性材料非线性饱和引起的信号失真问题。然而，当检测磁场时，它需要一个积分器。光纤电流传感器比电磁感应变压器和罗氏线圈具有更宽的频带响应范围和更好的电气绝缘特性。然而，它容易受到温度和振动的影响，已成为制约其推广的瓶颈。它需要激光器和调制器，因此系统复杂、成本高、体积大。

近年来，由于磁致伸缩/压电复合材料具有很强的磁电耦合且易于制备，受到了广泛研究[5-6]。磁电复合材料是制作高灵敏度、高分辨率磁传感器件的理想功能材料，其灵敏度高于霍尔元件与超磁阻传感器，频率范围比磁通门大；虽然灵敏度比超导量子干涉仪小，但是其结构简单、制备容易、成本低、可在室温下使用[7]。由于磁致伸缩材料的偏置磁场依赖特性，其可作为直流磁场传感器[8-10]；在外部交流磁场下，磁致伸缩相施加机械应力，然后转移到压电相，产生交流电荷输出，其可作为交流磁场传感器[11-12]、位移传感器[13-14]、电流传感器[15-21]、转速传感器[22]。然而，迄今为止，对磁电复合传感器进行的大多数理论和实验研究都是在静态磁场和标准正弦波磁场激励的前提下进行的[1-22]。因此，为了扩展磁电复合材料在电力系统雷击、故障等瞬态电流测量领域中的潜在应用，有必要对磁电复合材料在瞬态磁场/激励激励下的磁电响应开展研究。

本文利用有限元仿真元件，分析FeGa/PZT圆柱体磁电复合材料在8/20 μs雷电激励下磁电响应，为磁电复合材料在雷电测量领域提供理论分析基础。

1 有限元仿真模型建立

为充分研究FeGa/PZT磁电复合材料在8/20 μs雷电激励下磁电响应，本文将利用有限元分析软件Comsol对其进行模拟分析。本文分析的FeGa/PZT圆柱体磁电复合材料结构如图1(a)所示。利用Comsol软件直接对FeGa/PZT复合结构进行建模，采用二位轴对称进行模型建立，结构如图2(b)所示。其参数为12 mm×16 mm(Lp×Lm)，其中tm和tp分别为2和0.5 mm，结构两端均为自由状态。图中隐藏了所建立的空气域与线圈几何模型，空气域为半径为90 mm、高度为180 mm的圆柱体。线圈为内径10 mm，外径10.5 mm，高度为50 mm的圆管形，磁电复合结构置于其中心处，线圈中的施加的激励电流采用外部电流密度。磁致伸缩材料根据FeGa材料参数自行设置，压电材料选取库中的PZT-5H。

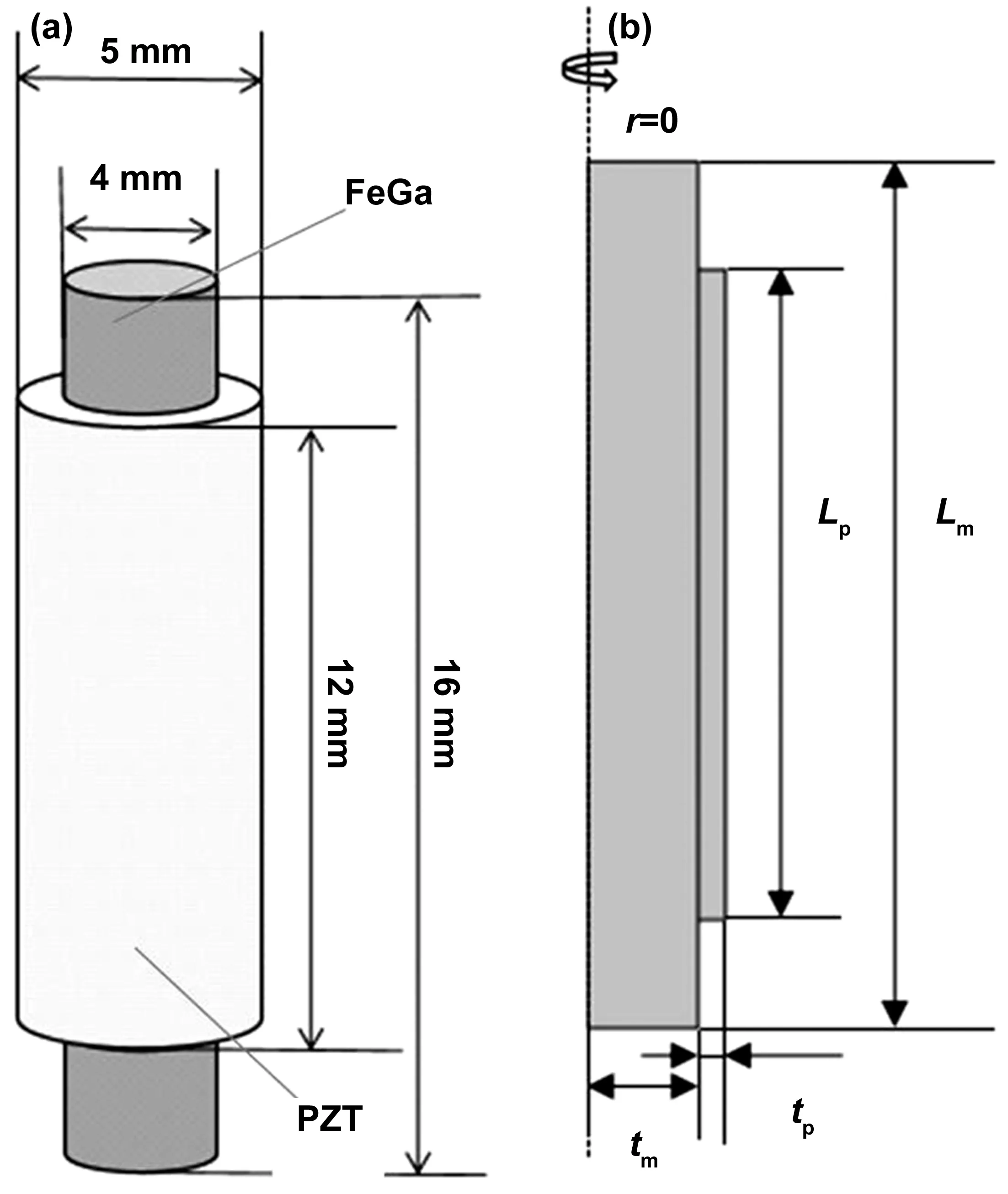
图1 (a)磁电复合结构几何模型 (b)网格划分后几何模型Fig.1 Geometric model of the magnetoelectric composite before and after lattice division

仿真中，对磁致伸缩材料、压电材料以及线圈采用自由四边形网格划分，设置最大单元大小为0.75 mm，其余剩余空气域采用默认的自由三角形网格划分。网格划分完成后如图1(c)所示，图中隐藏了线圈以及空气域。

2 正弦交流激励下磁电响应仿真分析

首先，利用COMSOL中频域求解器对所建立磁电复合材料的谐振频率进行求解。设置线圈中外部电流密度为1 000 A/m2，交流电流频率从1 kHz变化到400 kHz，在求解器中设置所选频段内选取400个点。求解结束后，为获得磁电复合材料的输出电压，对压电管内壁建立二维数据集，其性质选择加和。

在COMSOL软件的结果选项中选择一维绘图组，数据源选择已经建立的二维数据集，选择点图绘制之后得到压电管正极电势随交流激励频率变化如图得2所示。由于压电管外壁为接地，电势为0，因此压电材料的输出电压即为其正极电势。从图2中可以看到，磁电复合材料在一阶谐振频率100.36 kHz时输出电压达到最大，约为1.15 V，在二阶、三阶谐振频率处输出电压约为0.1 V，远远小于一阶谐振频率处的输出电压。

随后，对磁电复合结构谐振振动模态进行了分析。复合材料在一阶谐振、二阶谐振和三阶谐振处的振型如图3所示。从图中可知，在一阶谐振频率100.36 kHz时，整个结构明显处于沿轴向的拉伸状态，而在二阶、三阶谐振频率下，有很明显的弯曲和扭转现象。综上可知，磁电复合材料的主振模态为纵波振动，频率为100.36 kHz，或固有周期为9.964 μs。

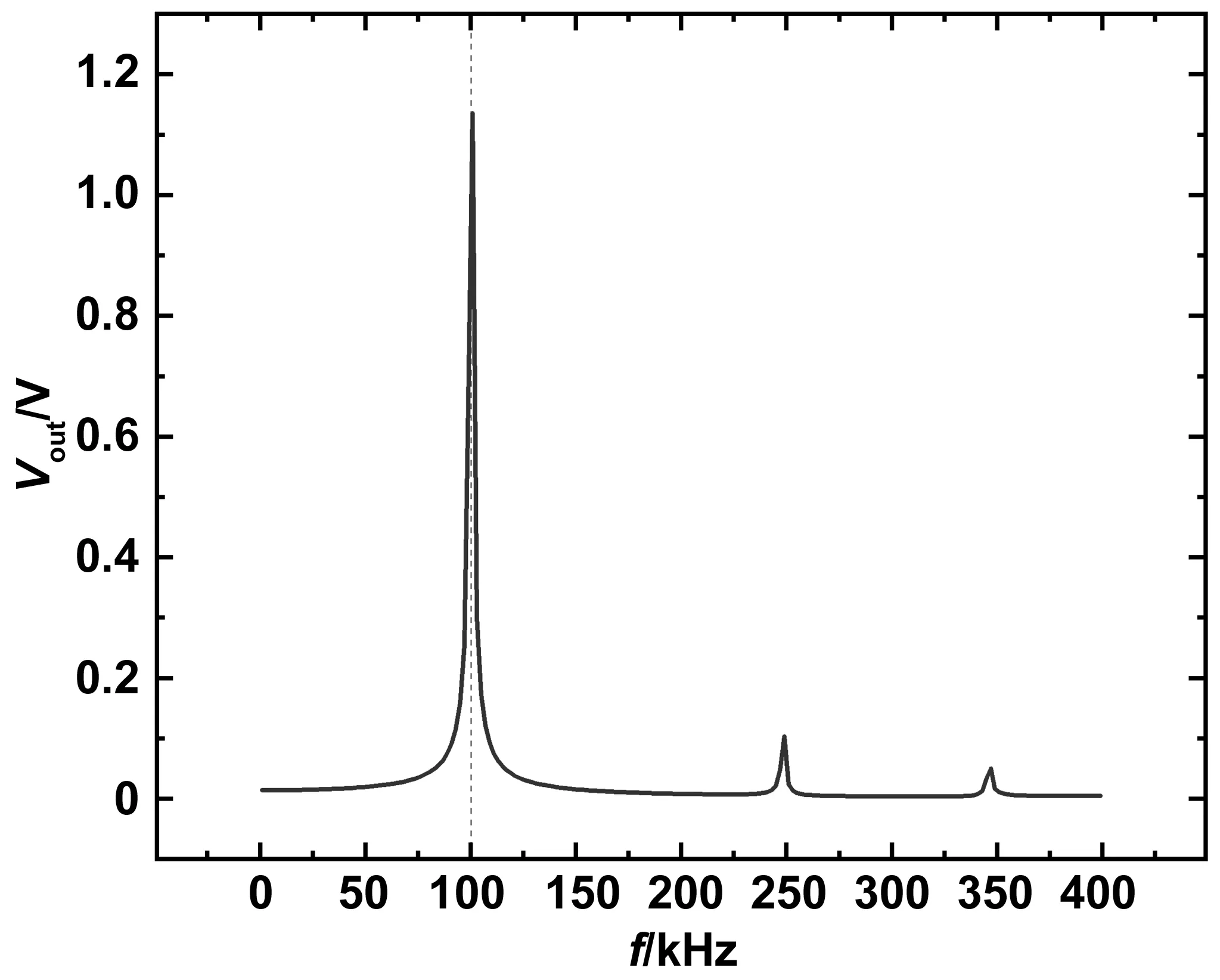
图2 磁电复合材料输出电压随激励频率变化曲线Fig.2 Output voltage of the magnetoelectric composite as a function of the AC current frequency

图3 磁电复合结构(a)一阶、(b)二阶和(c)三阶振动模态Fig.3 First, second and third order vibration modes of the magnetoelectric composite

3 8/20 μs雷电流双指数函数模型

描述8/20 μs雷电流的函数有多种，常用的函数模型有双指数函数模型、Heidler函数模型和脉冲函数模型。本文仿真中，采用双指数函数模型作为雷电流瞬态激励信号，如公式(1)。

(1)

根据公式(1)，绘制雷电流时域波形如图4所示，由于在仿真分析中只能使用函数作为电流激励源，因此其波形与国家标准8/20 μs雷电流的波形不太相同。从图中可知，电流从0 μs开始迅速上升，在约12 μs时达到峰值，随后逐渐下降，在约100 μs时已经完全降为零。

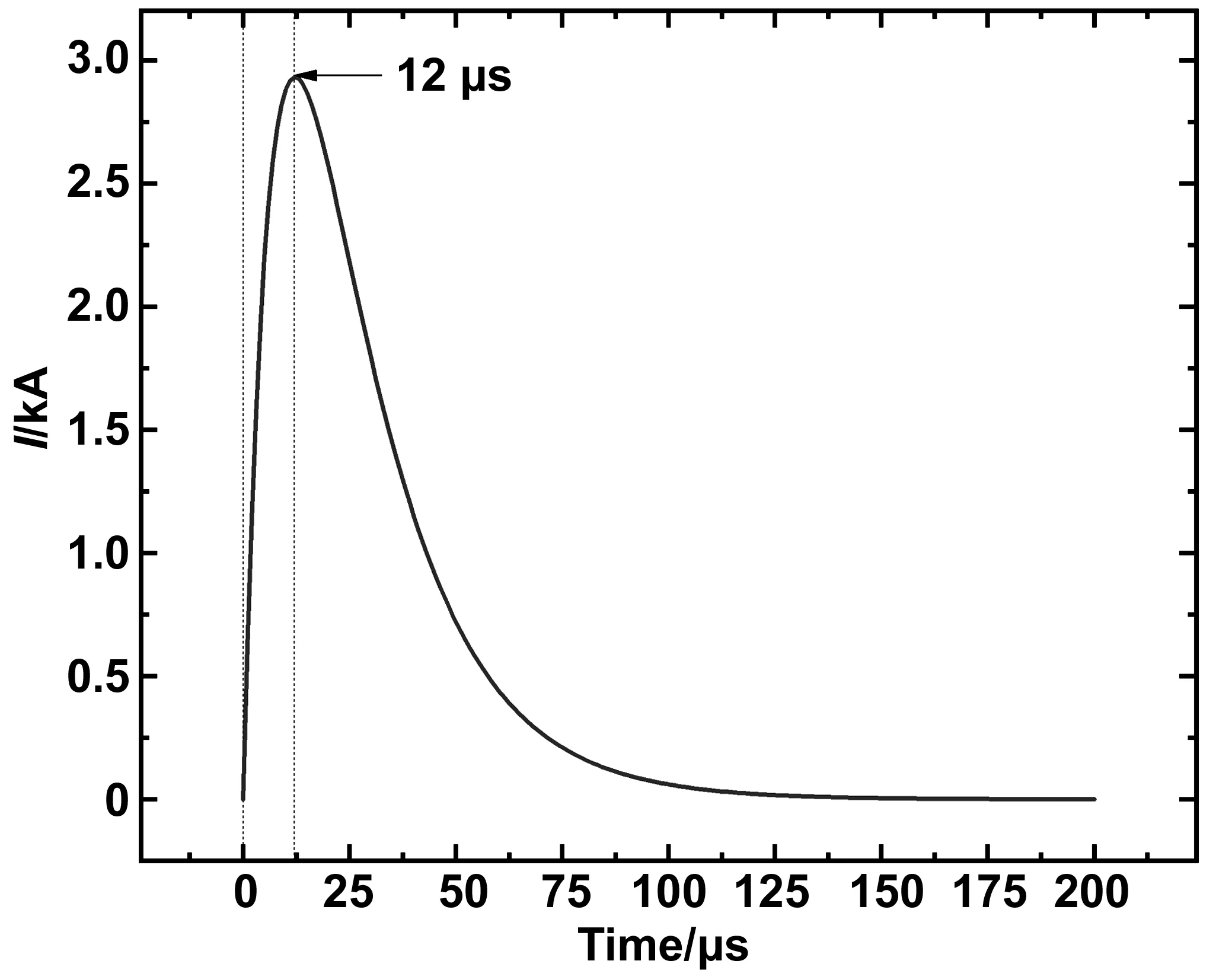
图4 8/20 μs雷电流双指数函数模型Fig.4 Double exponential function model of 8/20 μs lightning current

3.1 8/20 μs雷电流激励下，FeGa/PZT磁电复合材料时域波形

在8/20 μs雷电流激励下，将瑞利阻尼中质量阻尼参数设置为200，刚度阻尼参数设置为8e-8。计算求解之后，得到FeGa/PZT磁电复合材料输出电压曲线如图5所示。从图中可以看到，磁电复合材料的输出电压从零点开始迅速增加，由于振荡的影响，在9 μs时达到峰值，之后逐渐下降到零点，并在下降过程中伴随很明显的振荡现象，振荡周期为10 μs。输出电压到达峰值的时间比激励电流源提前3 μs，这是由于在上升过程中也伴随振荡现象，在9 μs刚好处于振荡中，因此造成了峰值提前。

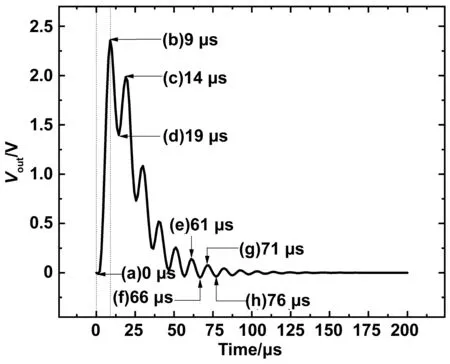
图5 8/20 μs雷电流激励下，磁电复合材料的输出电压Fig.5 The output voltage of magnetoelectric composite driven by 8/20 μs lightning current

由此可知，在8/20 μs雷电流激励下，FeGa/PZT磁电复合材料存在阻尼振荡现象，振荡频率等于材料一阶纵波振动频率(100.36 kHz)。这可以解释为，FeGa/PZT磁电复合材料是机械惯性器件，在脉冲激励下会发生阻尼振荡。

3.2 8/20 μs雷电流激励下，FeGa/PZT磁电复合材料不同时间的位移与电势分布

图5中(a)、(b)、(c)和(d) 4点分别为步点0、9、14、19 μs，经过后处理后得到该四点的电势分布如图6所示。可以看到在0 μs时，压电层电势分布整体为0；在9 μs时电势达到最大值，通过旁边图例可看出其电势分布大于另3点；在14和19 μs时分别处于振荡的波谷与波峰，因此19 μs时的电势分布明显大于14 μs。

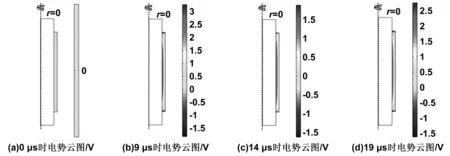
图6 分别在0、9、14和19 μs时压电层电势分布云图Fig.6 Cloud diagram of piezoelectric layer potential distribution at 0, 9, 14 and 19 μs

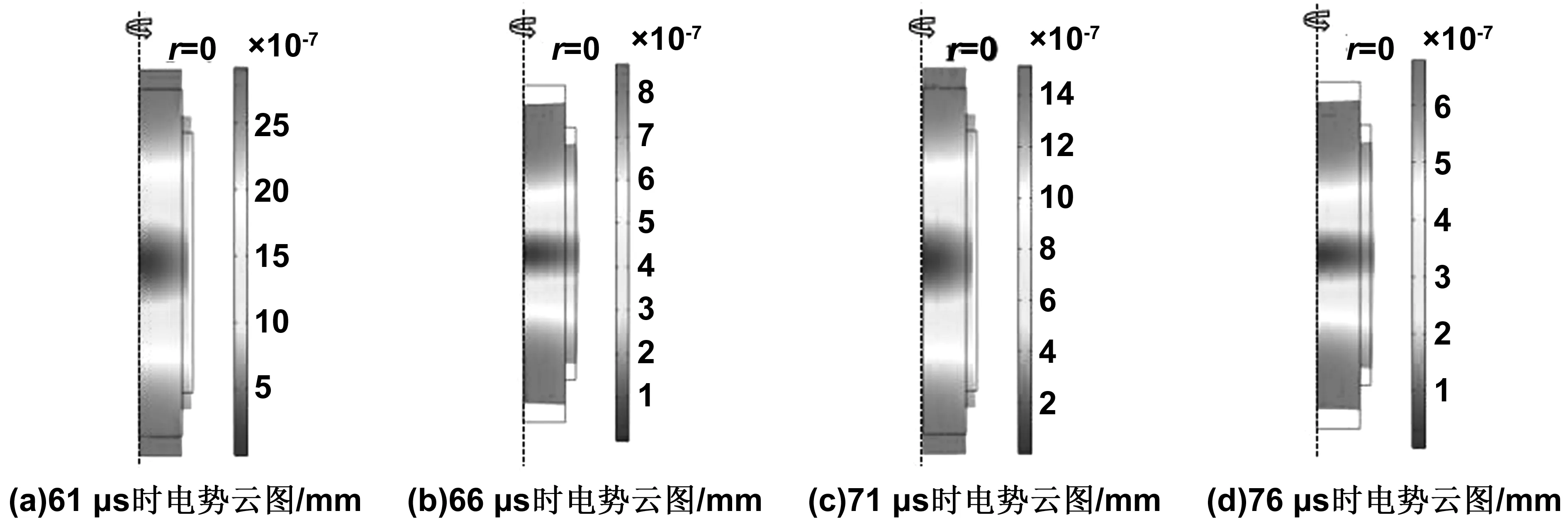
图7 分别在61、66、71和76 μs时位移图Fig.7 Displacement diagram at 61, 66, 71 and 76 μs

图5中(e)、(f)、(g)和(h)4点为步点的61、66、71、76 μs，均处于输出电压趋于稳定过程中，通过后处理对其机械状态进行查看得到其位移图如图7所示。可以看到磁电复合材料处于不断伸缩状态中，且由于在趋于稳定的过程中，因此每一个峰值或波谷的位移均比上一个峰值或波谷的位移小。

3.3 8/20 μs雷电流激励下，FeGa/PZT磁电复合材料幅值传感特性分析

接下来，对8/20 μs雷电流激励下磁电复合材料的输入输出特性进行仿真分析，通过设置雷电流峰值由0.5 kA增加到10 kA，得到其输出电压峰值变化如图8所示。在0.5 ～10 kA范围内，FeGa/PZT磁电复合材料输出电压峰值Vp与8/20 μs雷电流峰值Ip拟合关系为

Vp=0.0018×Ip-2.3406,R2=0.9855

(2)

由此可知，FeGa/PZT磁电复合材料可用于8/20 μs雷电流峰值测量。

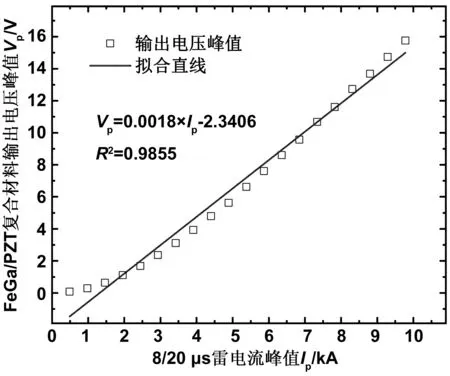
图8 8/20 μs雷电流激励下，磁电复合材料的幅值传感特性Fig.8 Amplitude sensing characteristics of magnetoelectric composites driven by 8/20 μs lightning current

4 结 论

通过时域分析研究了在8/20 μs雷电流激励下FeGa/PZT磁电复合材料的瞬态响应特性。在8/20 μs雷电流激励下，磁电复合材料的输出有较为明显的振荡现象，振荡频率等于材料一阶纵波振动频率(100.36 kHz)。这可以解释为，FeGa/PZT磁电复合材料是机械惯性器件，在脉冲激励下，会发生阻尼振荡。在0.5kA到10kA范围内，FeGa/PZT对8/20 μs雷电流峰值灵敏度达到1.8 mV/A，线性度达到98.55%。以上仿真分析结果证明磁电复合材料在瞬态电流测量领域有良好的应用前景。