基于AdvantEdge加工的M2高速钢微铣削力仿真与预测
叶文珺, 钱 炜
(上海理工大学 机械工程学院, 上海 200093)
在摩擦副表面通过加工微织构来获得流体动压效应,提高摩擦副润滑性能,减少摩擦磨损。目前所加工的织构大部分采用激光加工,激光加工效率虽高,但是现阶段只停留在实验室阶段;在本课题中,课题组决定采用加工中心,用微小径铣刀铣出凹槽。刘宇等[1]用不同刀刃半径的微铣刀对AL6160工件进行铣槽,进行三维仿真模拟并获取仿真切削力。折小荣[2]用有限元分析软件AdvantEdge分析了切削用量和钝圆半径对45号钢铣削过程中刀具的温度变化。
在切削过程中切削力和切削温度会影响刀具磨损、加工精度及工件材料的性能等[3-5]。因此研究切削用量对切削力和切削温度带给工件和刀具的影响对提高加工质量及刀具的寿命很有意义。
课题组以M2高速钢为被加工材料,硬质合金为铣刀材料,用0.3 mm的微小径铣刀加工微凹槽;通过AdvantEdge进行正交实验仿真,以最小铣削力为目标对结果进行分析。通过对切削力的分析,为铣削M2高速钢提供合适的切削用量。
1 切削模型的建立
1.1 材料参数
高速钢是高速工具钢的简称,是一种重要的刀具材料,因其在高温下也能保持它的高耐磨性,因此也用在一些重要轴承中。高速钢属于高碳高合金莱氏体钢,由于其独特的合金成分和后续的热处理工艺而使其具有优异的综合力学性能。热处理后,高速钢可以获得很高的硬度(HRC63~70)和高耐磨性,当温度达到500~600 ℃时,仍然能保持高硬度。M2高速钢的成分及力学性能如表1和表2所示。

表1 M2高速钢化学成分

表2 M2高速钢力学性能
1.2 材料本构方程
材料的本构方程反映工程材料在切削中的应力应变及应变率随温度的变化。本构模型有很多种,如Johnson-Cook模型、Zerilli-Armstrong模型、Drucker-Prager模型和Power-Law模型等。由于Johnson-Cook模型参数较少,模型结构简单,笔者选择Johnson-Cook模型,其本构方程为:
(1)
式中:A为屈服应力,MPa;B为加工硬化模量,MPa;C为应变敏感系数;t为硬化系数;m为材料热软化系数;Tmelt为材料熔点,℃;Troom为室内温度,℃;ε为应变;ε0为参考应变。
A,B,C,m和t为5个待定的材料参数。其中:A,B和t是材料应变强化项的系数,其值越大表示材料硬化程度就越高;C表示材料的应变速率强化项的系数,反映的是流变应力受应变速率影响的程度;m反映材料流变应力对温度变化的敏感程度。式(1)中等号右边的3个式子分别表示材料的应变强化效应、材料的应变速率强化效应以及材料的热软化效应。查阅文献[6]可知A,B,C,m和t5个模型参数的数值如表3所示。

表3 J-C本构方程参数
1.3 仿真软件参数设置
利用仿真软件AdvantEdge,建立三维铣削模型。由于采用微铣削,设置的铣削径向宽度为0.3 mm,刀具直径0.3 mm,刀刃半径0.001~0.004 mm,刀刃前角5°~8°。刀具材料选择硬质合金,工件材料为M2高速钢,初始温度为20 ℃,铣削模型如图1所示。

图1 铣削仿真参数设置
2 正交实验
影响铣削力的因素很多,大部分会考虑切削3要素,但由于微铣削不同于传统切削,当刀刃圆弧半径小于切削厚度时,切削过程中不产生切屑而是对被加工表面进行挤压;而刀具前角也影响着切削的难易程度,间接影响切削力,因此也是需要考虑的因素。为了减少试验次数,达到与大量全面试验等效的实验结果,因而采用正交实验。本实验为5因素(主轴转速、每齿进给、轴向切深、刀刃半径、刀具前角)4水平的正交实验,由于轴向的切削力较小,省略不计,只研究径向的2个方向的切削力,通过AdvantEdge仿真软件得到切削力Fx和Fy,如表4所示[7-10]。
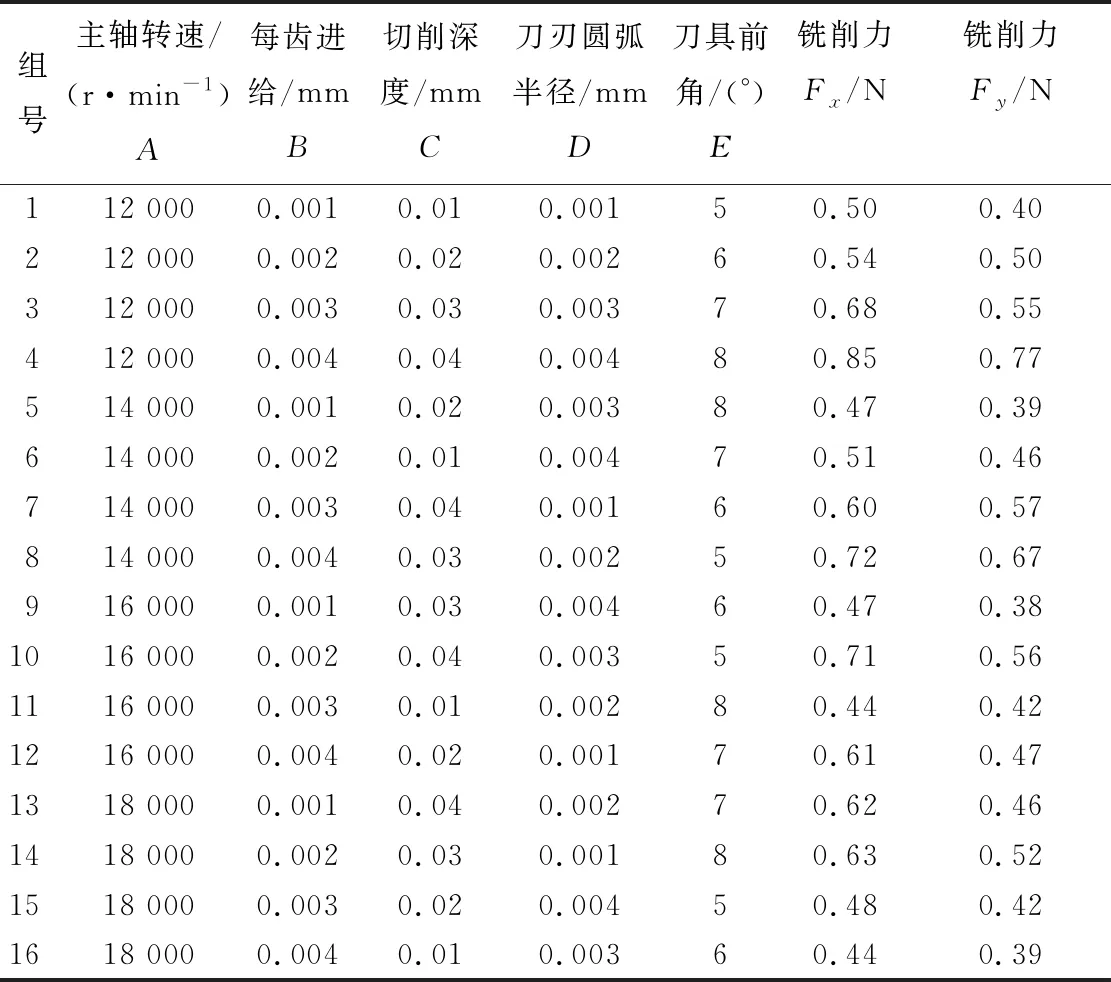
表4 正交实验结果统计表
对以上正交表,用Minitab分析田口得到如表5所示的均值响应表。δ值的计算原则是:通过对因子取最大和最小特征平均数之差来测量效应的大小。表5中的秩有助于快速确认哪些因子的效应最大[11-12]。给予δ值最大的因子以秩1,给予δ值第2大的因子以秩2,依此类推。从表5可以看出,对铣削力的影响大小为:切削深度>每齿进给>主轴转速>刀具前角>刀刃圆弧半径。再用多响应预测分析得到最优解如表6所示。切削力最小的组合为:主轴转速18 000 r/min,每齿进给0.001 mm,切削深度0.01 mm,刀刃圆弧半径0.004 mm,刀具前角8°。并预测最优解的铣削力Fx和Fy。
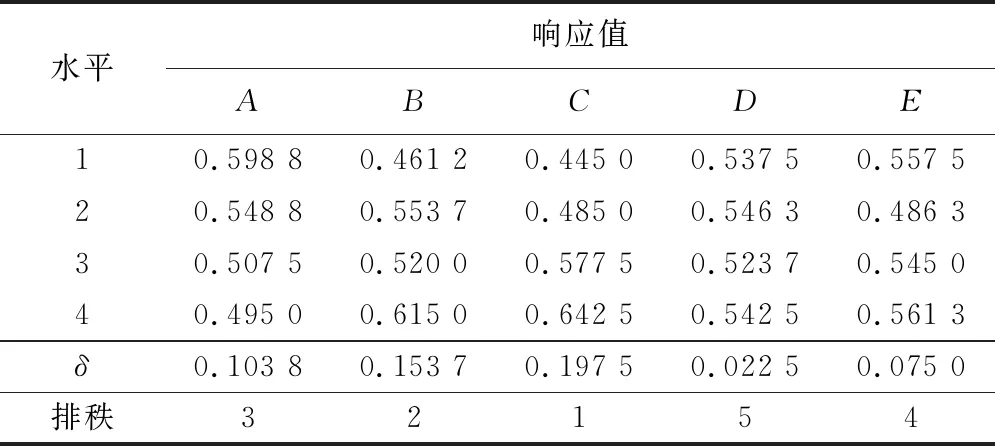
表5 均值响应表

表6 多响应预测
3 多元线性回归模型的建立
课题组采用指数形式的切削力与切削参数之间的关系式为:
(2)
式中:ε为总修正系数,ap为轴向切削深度,n为主轴转速,fz为每齿进给量,r为刀刃半径,γ为刀具前角。
对式(2)的2边求对数,可得:
lnF=lnε+n1lnn+n2lnfz+n3lnap+n4lnr+n5lnγ。
(3)
令Y=lnF,b=lnε,X1=lnn,X2=lnfz,X3=lnap,X4=lnr,X5=lnγ,式子(3)可写为:
Y=b+n1X1+n2X2+n3X3+n4X4+n5X5。
(4)
式(4)为多元线性方程,把表4中的数据代入式(4),用MATLAB算出各系数,可得:
(5)
表7为该数学预测模型的模型统计表。其中包括R2统计量、F统计量、P值以及误差方差K的估计值。R2值代表模型的拟合程度,表明2个方向的铣削力拟合程度都在70%以上,P值都小于0.05,拟合效果显著。将表6多响应预测的最优解代入式(5),得到拟合值Fx=0.27,Fy=0.28,取拟合后的铣削力值。

表7 模型统计量表
4 M2高速钢微铣削实验
4.1 实验设计
试样选用20 mm×20 mm×6 mm的六面体M2型的高速钢,硬度为HRC 60~63,0.3 mm的硬质合金微小径铣刀,刀刃半径0.004 mm,前角5°。装夹时夹头离微小径铣刀的刀头近一些,使悬臂刀刃尽可能小。为了保证切削中的平稳,需要保证工件的平面度,采用磁吸底座吸附工件,磁吸底座每平方厘米可吸附250 N的力,并将Kistler 9347C测力仪放在磁吸底座下面,在数控机床上采用全径铣削加工铣槽。实验中采用型号为FANUC ROBODRILL的加工中心,主轴最高转速为24 000 r/min。实验设备如图2所示。

图2 实验设备
4.2 实验结果及对比
对上文中数学模型预测的最佳参数以及正交实验中所选最佳一组参数进行实验验证,选用表4正交实验第15组的参数,以及根据预测模型式(5)和多响应预测的最优解分析得到的铣削力。实验中每组数据测3次,取平均值,得到如表8所示的结果。从表8中可以看出,实验值和仿真预测值误差在10%以内,可以有效预测铣削力。

表8 实验数据与仿真预测数据对比
5 结论
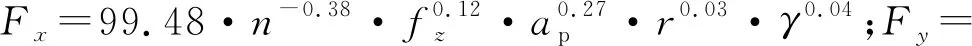
——分清“主”和“次”

