基于阿马加分体积定律的高压氦氮混合气配制方法

赵婉瑄， 宋薛思， 彭文珠*， 胡 军， 顾超华， 韩 冰

(1.浙江大学 化工机械研究所， 浙江 杭州 310027；2.大连锅炉压力容器检验检测研究院有限公司 国家市场监管重点实验室(气瓶安全技术)， 辽宁 大连 116013； 3.浙江大学 流体动力与机电系统国家重点实验室， 浙江 杭州 310027)

氢能是世界能源转型升级的重要载体，是我国未来能源体系的重要组成部分，高效、安全的氢能储输是氢能大规模应用的前提[1]。高压储氢由于设备结构简单、压缩氢气制备能耗少和充装速度快等优点成为目前的主流储氢方式。其通过提高压力的方式提高储能密度，但是压力越高则潜在泄漏和爆炸风险愈高。为保障高压氢气瓶的服役安全，需要在出厂前进行气密性测试[2]。考虑到高压氢气作为测试气体的危险性，高压氢气瓶气密性测试通常采用氦检漏技术。氦检漏灵敏度高、仪器响应快，是目前应用最为广泛的检漏方式[3]。由于纯氦气价格较高，通常使用高压氦氮混合气作为检测气体，以降低气密性检测成本。相关研究表明[4-5]，混合气的氦摩尔分数直接影响氦泄漏率的检测结果，精确配制高压氦氮混合气是获取准确氦泄漏率的重要前提。

1 混合气配制方法

混合气广泛应用于能源、环保、工业、电子和医学等行业[6]，常用的混合气配制方法有动态法[7]、静态法[8]、分压法[9]、称量法等[10]，对不同的使用场景，需要根据气体混合物的气体性质、浓度范围、准确度和不确定度等因素的要求，灵活选用配气方法。

各方法的优缺点如表1所示。其中，动态法配制精度高，但因其仪器设备复杂，不适合配制高浓度的气体，通常只用于配制特殊混合气，如极性气体、易冷凝组分和极低体积分数混合气；静态体积法配气速度快、操作简单，但由于压力和温度修正的不确定性导致配制的重复性和准确性较差，一般用于需求量小的气体配制；称量法通过控制各组分质量来控制各组分气体的摩尔质量分数，但同样对设备和操作的要求较高，适合配制高精度、常压的少量混合气。相比其他配制方法，压力法配制成本低、操作简单且配制速度快，更适用于高压氢气瓶的检漏气体配制[11]。需要注意的是，压力法以道尔顿分压定律为基础，对于低压混合气而言具有较高的准确性，然而真实气体的压缩因子会随着压力的升高而改变，应用此方法配制高压混合气时，准确度不够理想，需对气体压缩系数等因素进行修正。

表1 混合气配制方法

2 氦氮混合气配制方法

2.1 气体混合法则

气体混合物的组成和成分千差万别，需利用组成混合物的各纯物质的参数，通过气体混合法则来计算混合物的性质或其他热力性质，并确定其状态方程。常用的气体混合法则有道尔顿定律[12]和阿马加分体积定律[13]。

2.1.1 道尔顿分压定律

道尔顿分压定律假设混合气体的总压力等于各组分的分压之和，且混合物的各纯物质体积等于气瓶容积。当混合气为二元混合气时，组分1和组分2的分压计算公式为：

p1=p×C;

(1)

p2=p×(1-C)。

(2)

式中：C为氦摩尔分数，p为混合气压力，p1为组分1分压，p2为组分2分压。

因组分1和组分2体积均等于气瓶容积，混合气的摩尔体积计算公式为：

(3)

式中：V为气瓶体积，ρ1为组分1分压p1和混合气温度T对应的组分1的摩尔浓度，ρ2为组分2分压p2和混合气温度T对应的组分2的摩尔浓度。

由道尔顿分压定律计算的混合气压缩因子如下：

(4)

式中：R为气体常数，T为混合气温度。

2.1.2 阿马加分体积定律

阿马加分体积定律假设混合气体的总体积等于各组分的体积之和，混合气的摩尔体积和气体压缩因子的计算公式如下：

Vt-A=V1×C+V2×(1-C);

(5)

(6)

式中：V1为混合气压p和混合气温度T对应的组分1的摩尔体积，V2为混合气压p和混合气温度T对应的组分2的摩尔体积。

选用Miller[14]和Canfield[15]的实验数据，通过NIST数据库[16]查询指定温度和压力下的气体摩尔浓度，分别代入式(4)和式(6)，计算道尔顿定律压缩因子ZD和阿马加定律下的压缩因子ZA，并将计算结果与实验测得的压缩因子Z进行对比，如表2所示。

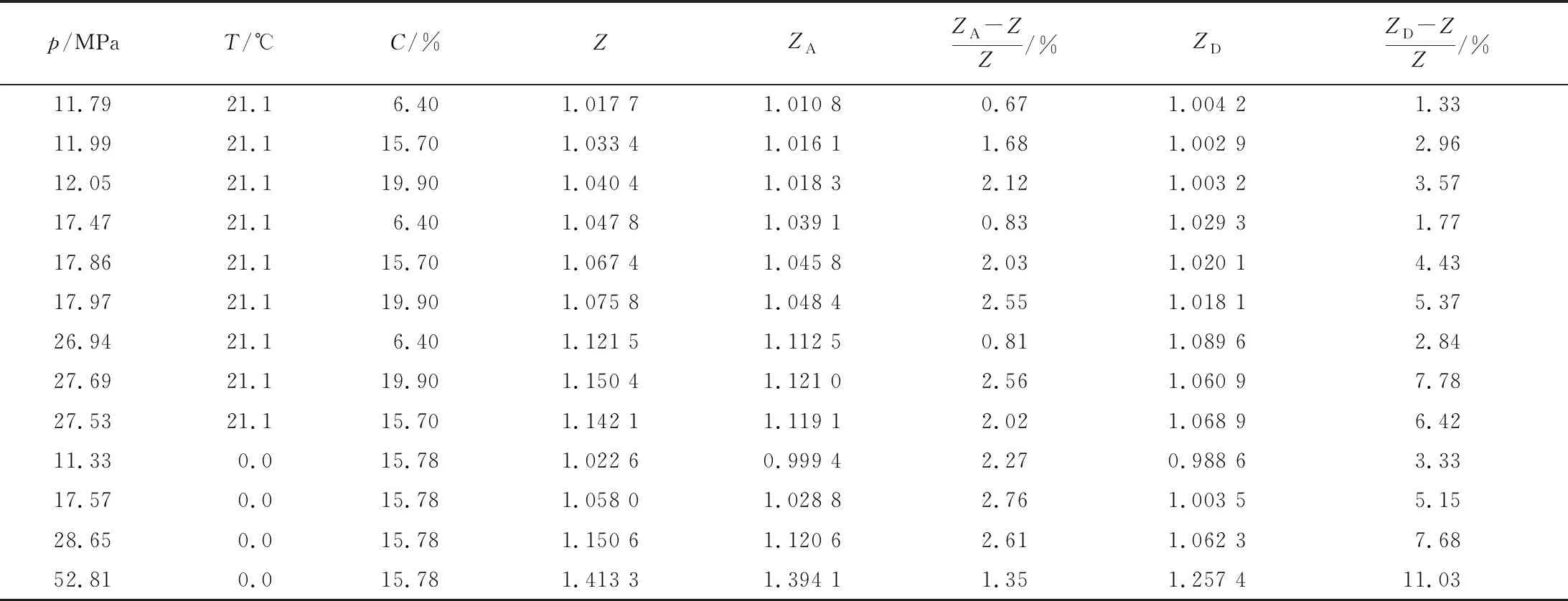
表2 理论气体压缩因子与真实气体压缩因子误差对比

由表中数据可知，随着压力的升高，通过道尔顿分压定律计算得到的高压混合气压缩因子误差增大，在0 ℃、52.81 MPa时，计算误差已超过10%。通过阿马加分体积定律计算的气体压缩因子误差受压力和温度影响较小，在表2所示的温度压力范围内其误差均在3%以下。相比道尔顿定律，阿马加分体积定律更能反应高压对氦氮混合气压缩因子的影响，可将其用于高压氦氮混合气组分比例的计算。

2.2 应用阿马加体积定律的混合气配制方法

根据压力法配制氦氮混合气的步骤，需先将氦气充入体积为V的配制气瓶直至压力达到PHe，记录此时气瓶内的气体温度THe;再向气瓶内充入氮气，待2种气体混合均匀后记录气瓶内混合气压力P和温度T。通过以下方法计算混合气中氦的摩尔分数。

2.2.1 混合气中氦的物质的量

混合气中氦的物质的量公式为：

nHe=ρHe×V。

(7)

式中：nHe为充填的氦的物质的量，ρHe为氦分压pHe和温度T对应的氦的摩尔浓度。

2.2.2 混合气中氮的物质的量

混合气中氦气的体积计算和混合气中的氮物质的量计算公式如下：

(8)

VN2=V-VHe;

(9)

nN2=ρN2×VN2。

(10)

式中：nN2为充填的氮的物质的量，VHe为最终混合气中氦气的体积，VN2为最终混合气中氮气的体积，ρHe-2为混合气压力p和温度T对应的氦摩尔浓度，ρN2为混合气压力对应的氮的摩尔浓度。

2.2.3 混合气中氦的摩尔分数

混合气中氦的摩尔分数C为：

(11)

由式(7)～(11)整理得到：

(12)

设计混合气配制方案时，可根据拟配制的混合气压力p和氦气摩尔分数C得到配制混合气时所需的氦摩尔浓度ρHe：

(13)

根据式(13)得到的ρHe，结合NIST数据库氦气的密度压力对应关系，可以得到充氦压力pHe。

考虑到真实气体压缩因子的影响，真实气体的摩尔浓度可通过NIST数据库查得。

3 高压氦氮混合气配制实验

3.1 实验装置

为验证上述配制方法的准确性，按照上述方法配制高压氦氮混合气，混合气配制装置如图1所示。实验过程中记录充氦压力pHe、充氦温度THe、混合气压力p和温度T，并使用气相色谱仪测得混合气中氦气的摩尔分数C0。

图1 混合气充装系统

3.2 实验结果分析

根据高压气瓶在进行气密性实验时的实验需求，利用图1所示混合气充装系统配制压力为35～80 MPa、氦摩尔分数为1%～20%的氦氮混合气，实验结果如表3所示。分别由式(1)和式(12)计算基于道尔顿定律的理论氦摩尔分数CD和基于阿马加分压定律的理论氦摩尔分数CA。

在表3所示实验温度压力范围内，道尔顿分压的氦摩尔分数误差最低为16.41%、最高则达到93.04%。实验结果表明应用道尔顿定律的氦摩尔分数计算精度受压力的影响较大，且由于计算过程中未考虑混合后的气体温升效应，实际的误差进一步增大。

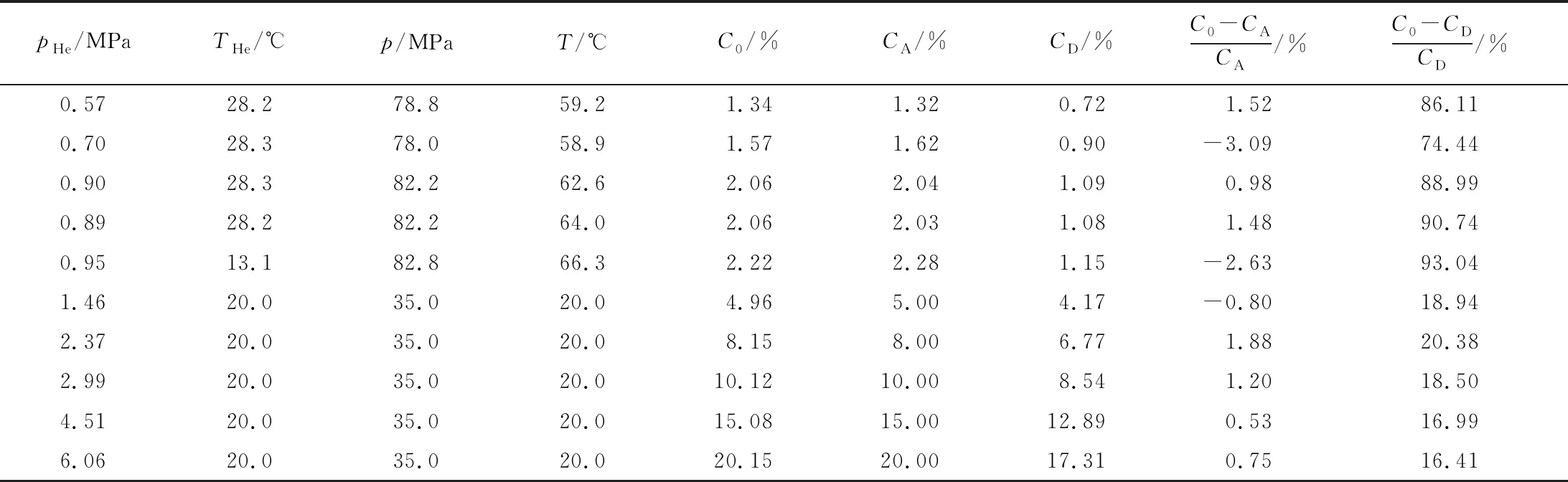
表3 混合气配制实验结果

应用阿马加分体积定律时，实测氦摩尔分数C0与理论氦摩尔分数CA之间的偏差均小于5%，当氦摩尔分数在5%～20%之间时，实测值与理论计算值之间的误差可控制在2%以内，且误差受气体压力和氦摩尔分数的影响较小。故进行氦氮混合气的配制方法设计时，可通过式(13)得到配制混合气所需的氦气压力。

4 结语

相比道尔顿分压定律，阿马加分体积定律考虑到配制过程中的温升效应和高压对真实气体压缩系数的影响，更适用于高压氦氮混合气组分比例的计算。课题组利用阿马加分体积定律在原有压力法的基础上进行改进，提出了氦氮混合气中氦摩尔分数及配制过程中所需氦气压力的计算公式，并通过实验验证该方法的准确性。实验结果显示：当氦摩尔分数在5% ～ 20%(覆盖气瓶气密性实验的常用浓度范围)之间时，基于阿马加分体积定律得到的氦摩尔分数误差<2%，可满足气瓶气密性实验的高压氦氮混合气配制需求。基于阿马加分体积定律的混合气配制方法准确、简单和可靠，具有实际应用价值。