灰狼算法优化VMD 与SVM 的滚动轴承故障诊断

蒋朝云，李亚，王海瑞

（650500 云南省 昆明市 昆明理工大学 信息工程与自动化学院）

0 引言

滚动轴承作为基础和关键部件之一，广泛应用于旋转机械，包括泵、电机、机器人、风力涡轮机和航空发动机[1]，随着机械设备可靠性和安全性的不断提高，对轴承的要求也越来越高。轴承经常在恶劣环境下运行，包括高温、意外冲击载荷和化学腐蚀，因此容易出现故障和后续故障。一旦发生轴承故障，机械设备瞬间受到影响，可能引发重大安全事故[2]，因此对滚动轴承故障进行诊断并及时采取维修措施是迫切和必要的。

如何从复杂振动信号中提取轴承磨损故障特征是轴承在线状态监测的关键。小波变换可用于分析具有灵活窗口（窗口函数大小不变但形状变化）的复杂信号。在有关研究中，韩芝星[3]等选用 Daubechies5 小波作为小波基，对提升机闸瓦间隙信号进行多分辨率分析，将突变信号进行多尺度分解，通过分解后的信号来确定突变信号的位置。然而，小波的时频分辨率受到海森堡测不准原理的限制，不能同时优化。小波基的选择对信号分析的结果影响很大；陈俊柏[4]等利用 EMD 提取振动信号不同频段的能量值作为特征参量，并结合压力信号均值构造故障特征向量，然而，经验模态分解缺乏严格的数学基础，抗噪声能力和模态混叠能力较差；郑国刚[5]等进一步对振动信号进行3 层小波包分解以及降噪处理，将处理后的剩余信号进行重构,找出所含剩余信息量较大的频段,进行EEMD方式分解，对分解后的IMF1 分量进行频谱和包络谱转换,从而准确提取出轴箱轴承故障特征信号。

EEMD 是一种改进的基于经验模态分解的分析方法，但仍不能避免端点效应，计算量大，去噪能力差。VMD 以完全非递归的方式实现了信号的频域分解和模态分量的有效分离，同时还具有分解能力强、去噪性能好、算法速度快的优点。但是VMD 分解效果受模态分量K和惩罚因子α的影响，K和α选取不当会导致分解度较低。

在构建算法模型时，由于模型参数众多，超参数选择将对分类结果敏感。针对超参数难以抉择的问题，研究人员运用群智能算法对众多超参数进行寻优。徐统[6]等针对滚动轴承早期故障的有效识别,提出了一种基于 VMD 瞬时能量与 GA 优化的 RBF神经网络的滚动轴承故障诊断方法；黄英来[7]等针对乐器音频信号识别率低的问题，提出了一种变分模态分解（VMD）和被粒子群算法（PSO）优化支持向量机（SVM）的乐器音频信号识别的方法；黄帅[8]等为了加强多绳摩擦提升系统的提升钢丝绳故障与提升钢丝绳张力之间的联系，提出了基于PSO 优化支持向量机（SVM）以及最小二乘支持向量机（LSSVM）的诊断模型。

上述超参数寻优方法寻优效果有限，使得最优适应度值容易陷入局部最优解，同时算法计算较为复杂，收敛速度受到严重影响。针对上述问题，本文提出一种GWO 优化VMD 和SVM 的故障诊断方法。对比同类型的优化算法，本文实验模型的迭代效果以及寻优能力大大提高，并且能较好地对VMD 进行分解，从而消除模态混叠等现象。

1 变分模态分解理论基础

变分模态分解（VMD）是一种将单变量数据根据预定义模态数和惩罚因子分解成有限个固有模态分量（IMFs）的信号处理方法[9]，它能够根据实际情况自适应确定模态分解个数，在搜索和分解过程中，对每种模态的最佳中心频率和有限带宽进行自适应匹配，实现信号的有效分离，获得变分问题最优解[10]。原始信号x（t）可定义为

模式的选择基于变分模型，该模型旨在最小化所有模态的带宽之和。在分解过程中，保证分解序列为具有中心频率的有限带宽的模态分量,约束条件为所有模态之和与原始信号相等，则相应约束变分表达式为

式中：K——需要分解的模态数；{uk}，{ωk}——分解后的模态分量和中心频率。

引入Lagrange 算子，将约束变分问题转换为非约束变分问题，得到曾广Lagrange 函数：

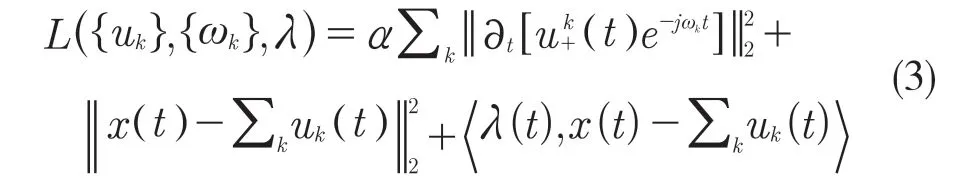
VMD 求解过程如下：

（1）n=0,初始化

（2）令n=n+1，开始执行循环程序。

（3）令k=0，k=k+1，按式（4），式（5）更新{uk}和{ωk}。

（4）更新λ：

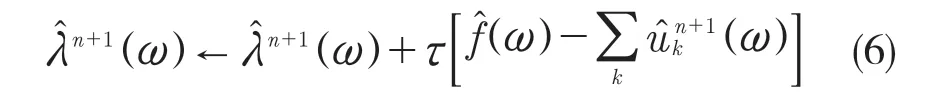
式中：τ——噪声容限能力。

（5）重复步骤（2）—步骤（4）直到满足式（7）。

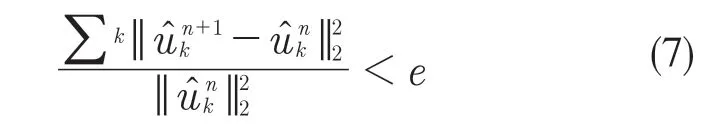
2 灰狼优化算法

灰狼是食物链顶端的食肉动物之一，他们有强大的社会结构，狩猎时遵循这个结构。按照优势度递减的顺序，狼群中的狼被分为alpha（α）、beta（β）和omega（ω）狼[11]。狩猎过程也分为3 个阶段：追踪猎物、追逐猎物、包围并攻击猎物。在GWO数学模型中，最适合的解被标记为alpha（α），其次是beta（β）和delta（δ），它们分别是第2 和第3 适合的解[12]。所有其他解决方案都是omega（ω）并遵循其他3 种。

包围猎物的过程是通过计算距离向量并使用它更新狼的位置建模，具体定义为：

个体与猎物间的距离公式

灰狼的位置更新公式

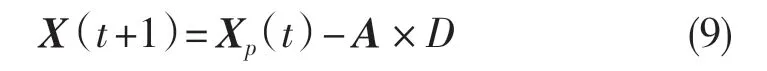
式中：t——目前的迭代代数；A，C——系数向量；XP和X——猎物的位置向量和灰狼的位置向量。

A 和C 的计算公式为：

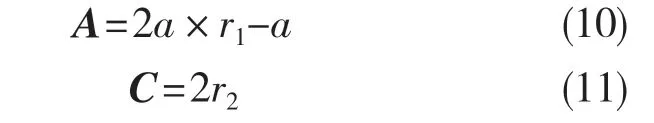
狩猎通常由α引导，偶尔由β和δ引导。

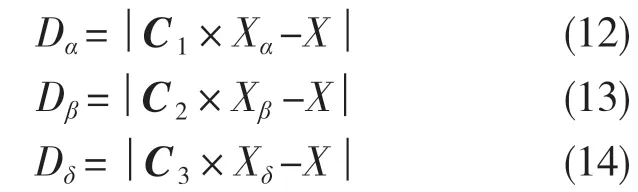
式中：Dα，Dβ，Dδ——α、β、δ与其他个体间的距离；Xα，Xβ，Xδ——α、β、δ的当前位置；C1，C2，C3——随机向量；X——当前灰狼的位置。

式（15）—式（17）分别定义了狼群中个体朝向α、β和δ前进的步长和方向：

式（18）定义了狼的最终位置：

为模拟逼近猎物，a的值逐渐减小，A 的波动范围也随之减小。在迭代过程中，当a从2线性下降到0 时，其对应的A 的值也在区间 [a，a] 内变化。如图1 所示，当A 的值位于区间内时，灰狼的下一位置可以位于其当前位置和猎物位置之间的任意位置；当|A|＜1 时,狼群向猎物发起攻击（陷入局部最优）；当|A|＞1 时,灰狼与猎物分离,希望找到更合适的猎物（全局最优）。

图1 狼群第3 阶段攻击图Fig.1 Attack diagram of the third stage of wolf pack

3 实验

实验采用美国凯斯西储大学轴承数据中心的轴承故障数据集。数据集为12 K 采样频率下的风扇端轴承数据，分别采集正常、内圈故障、滚动体故障、外圈故障（6 点钟方向）4 种不同状态的故障数据，除正常数据外，每种状态有3 种故障深度类型，直径分别为0.177 8，0.355 6，0.533 4 mm，轴承电机载荷为0，轴承转速为1 797 r/min，总共10 类故障类别作为本次实验的数据来源。每类数据划分为115 个分类样本，10 类总共1 150 个样本。训练集大小为700 份，即每类70 份，测试集为450 份，每类45 份。分类情况如表1 所示，其中RF、IF、OF 分别为滚动体、内圈、外圈故障（6点钟方向）。

表1 轴承数据解读Tab.1 Interpretation of bearing data

VMD 算法相较于EMD 及其他分解算法，模态分量具有较好的可分性，模态混叠现象较弱。但VMD 算法的分解结果受多个参数影响，其中模态数K及二次惩罚项α影响较大。因此，本文选用灰狼算法优化VMD 的2 个超参数，使2 个参数达到全局最优解，并以样本熵最小作为此次实验的优化策略。在寻优过程中，设置VMD 的K值搜索范围为[3，12]，设置α值的搜索范围为[10，2 500]，灰狼算法狼群数量为10，最大迭代次数为50。迭代图如图2 所示。

图2 VMD 迭代寻优结果Fig.2 VMD iterative optimization results

由迭代图可以看出，经过大约3 次迭代，达到最小适应度值2.936，并稳定在该值。同时，经过遗传算法优化后，VMD 的模态数和二次惩罚项分别为[10，200]。将2 个参数输入VMD 进行分解，取前8 个分量，分解效果如图3 所示。同时，将信号分别进行EMD 和EEMD 分解，与VMD 进行对比，其结果如图4、图5 所示。

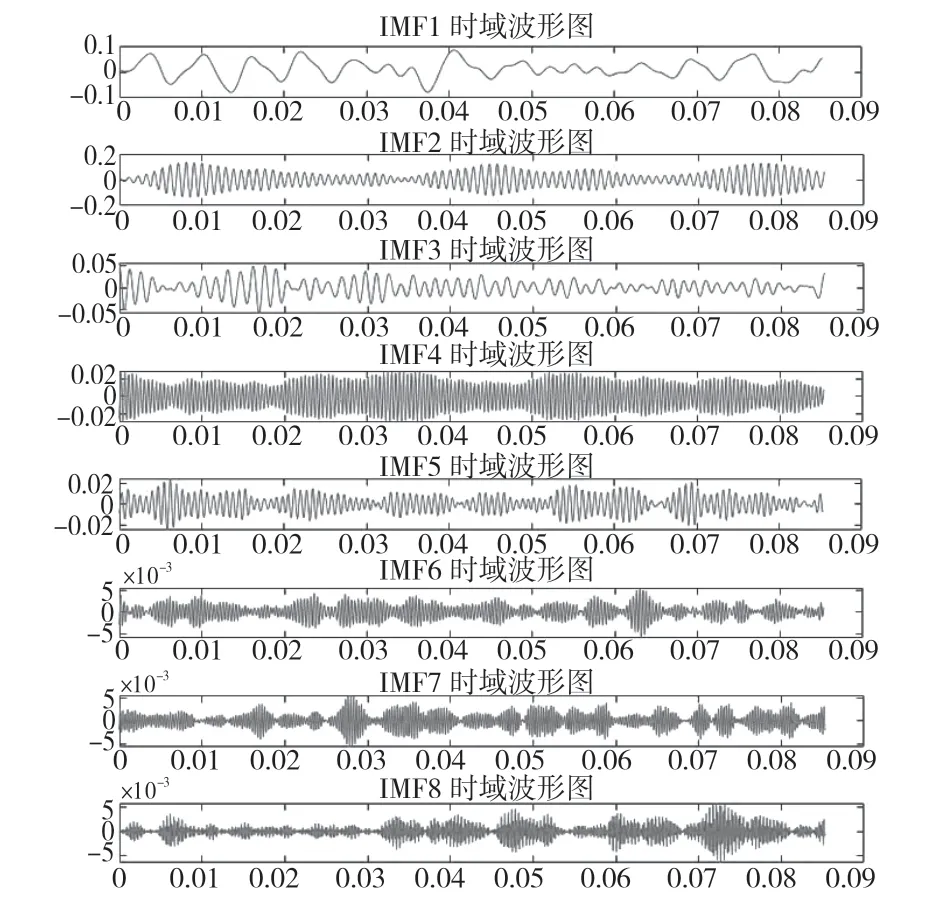
图3 VMD 分解效果Fig.3 VMD decomposition effect

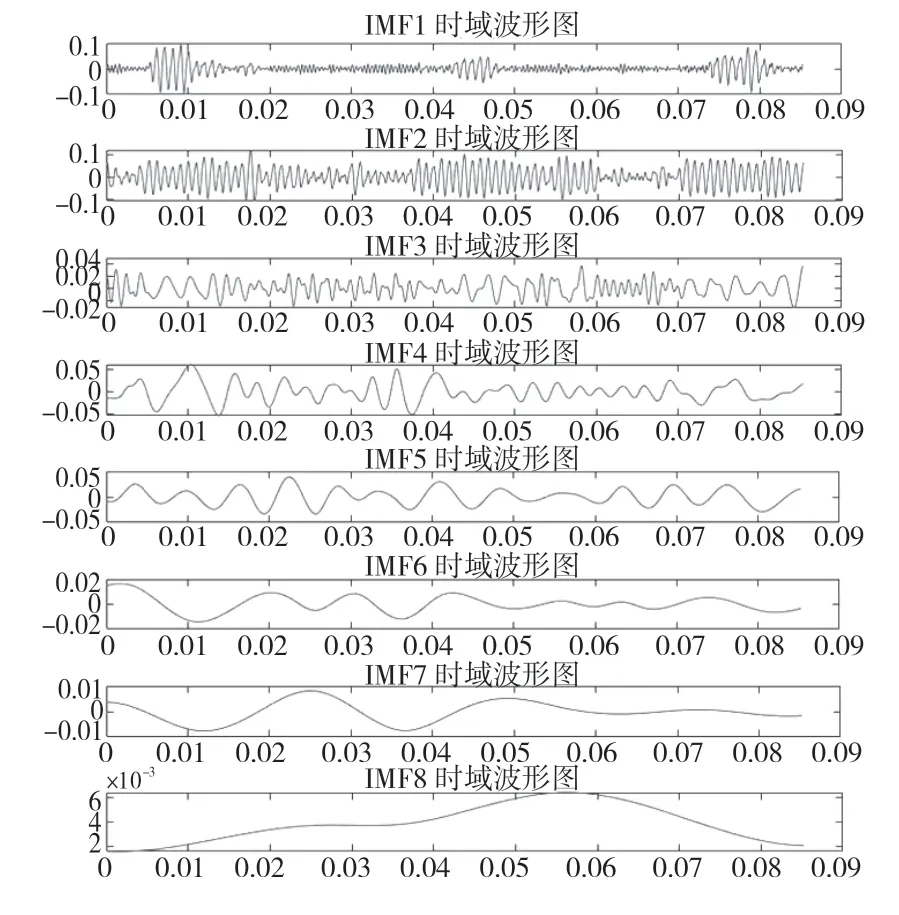
图4 EMD 分解效果Fig.4 EMD decomposition effect

图5 EEMD 分解效果Fig.5 EEMD decomposition effect

由图4 可知，原始信号经过EMD 分解后产生8 个分量。虽然EMD 可以广泛应用于非线性非平稳分析过程，但由于分解的局限性，多个分量均产生模态混叠现象。单独的IMF中全异尺度广泛存在，同时相同尺度信号则分布于不同分量，虽然信号被分解，但效果却被减弱，其冲击信号则因不同模态混合而被掩盖。EEMD 分解虽然对上述情况有所改善，但并不能较好解决上述问题。由图3 可知，通过VMD 分解后，分解出来的8 个分量均能明显地谐波分量，大部分波形接近正弦波，且波动较为均匀，是理想的时间分析序列。同时，由VMD 分解图可知，第7 和第8 分量振幅较小，振动频率较高，可判定2 个分量含有较多噪声。第2 至第6 分量大部分由高次谐波组成，频谱能量较为集中，含有的故障信息较多，因此本实验提取该分量集的能量和中心频率作为本实验的故障诊断输入向量。

由于数据集规模较小，因此采用SVM 对轴承故障特征进行分类，并运用GWO 算法对SVM 的惩罚因子C和核函数g进行优化。C的搜索范围为[0，100]，g的搜索范围为[0，100]，灰狼算法狼群数量为10，最大迭代次数为50 次，迭代图如图6所示。同时，本次实验进行5 折交叉验证，以提升模型泛化性能和精度，实际分类效果如图6 所示。

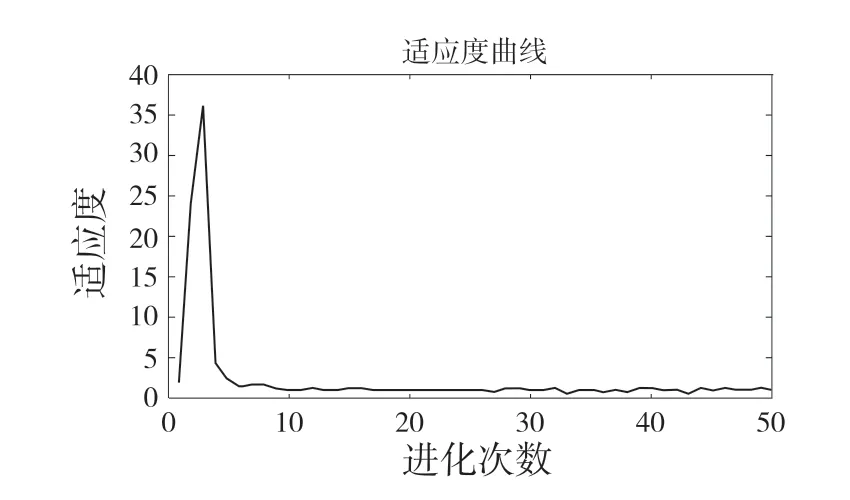
图6 GWO 优化SVM 迭代图Fig.6 GWO optimized SVM iteration diagram

经过灰狼算法寻优后，C和g的值分别为26.551 和9.98，用GWO优化SVM后用5 次迭代就可找到最佳适应度值，最佳适应度值为1.182。为了比较GWO 算法的收敛性能，用PSO 和GA 分别对惩罚因子C和核函数g进行优化。PSO 中，c为1.5，c2 为1.6，种群规模为30，最大迭代次数为50 次，其迭代图如图7 所示。GA 设置交叉概率选择为0.9，变异选择概率为0.1，种群规模为10，其迭代图如图8 所示。

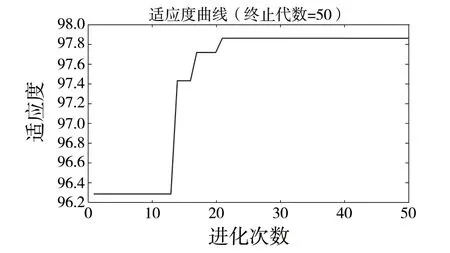
图7 PSO-SAM 迭代图Fig.7 PSO-SAM iteration diagram

图8 GA-SVM 迭代图Fig.8 GA-SVM iteration diagram

经过PSO 寻优SVM 超参数，需经过21 次才能达到最佳适应度值，在3 种模型中迭代代价最高；其次是GA 优化，需要9 次寻找到最佳适应度值；本文的模型在收敛性能中具有较好的优势，仅需5次便能达到最佳适应度值。表2 为3 种算法达到最佳适应度值所花费时间代价以及准确率对比。

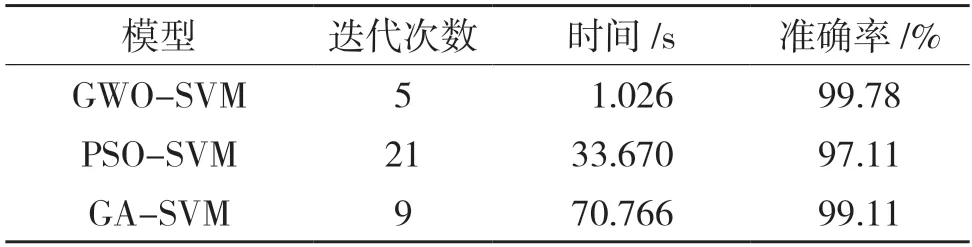
表2 模型性能对比Tab.2 Model performance comparison

由表2 可知，虽然GA-SVM 准确率可达99.11%，但在达到最佳适应度值时，GA-SVM 花费时间最长，需要70.766 s，训练效率较差；PSOSVM 虽然时间稍短但准确率仅为97.11%；GWOSVM 达到最佳适应度值仅需5 次，并且5 次迭代仅花费1.026 s，准确率可达99.78%，在3 种模型中最高。因此相较于两种优化算法，灰狼算法不仅收敛速度更快，而且就寻优精度而言也具有较大优势。

4 结论

针对VMD 算法模态数K及二次惩罚项α人为选取困难的缺点，提出一种GWO优化VMD的策略，利用GWO 优异的寻优能力，使信号进行高质量分解，消除模态混叠等不利影响。同时，由于SVM惩罚因子C和核函数g对故障判别有重大影响，提出用GWO 优化SVM 的方法，对比PSO 和GA，本实验所采取的方法具有较好的收敛性能和较高的分类精度。