面向CMOS温度传感器的低功耗数字滤波器设计
赵毅强 ,赵鑫宇 ,何家骥 ,李 尧 ,王帅鹏,耿俊峰
(1. 天津大学微电子学院,天津 300072;2. 天津市成像与感知微电子技术重点实验室,天津 300072; 3. 北京智芯微电子科技有限公司,北京 100192)
温度作为与生产生活密切相关的物理量之一,其感知技术在航空航天、生物医疗和电力电子等多领域被广泛应用[1-3].近些年,物联网技术的飞速发展使得无线低功耗传感节点得到了大量普及,基于CMOS工艺的温度传感器作为物联网温度感知节点的重要元件,应不断向低功耗方向发展.CMOS温度传感器的核心电路通常由感温电路、Sigma-Delta 调制器电路和数字滤波器电路3部分组成[4],其中,感温电路和Sigma-Delta调制器电路决定了温度传感器的精度;数字滤波器电路则直接影响了温度传感器的面积和功耗.因此,设计低功耗数字滤波器电路是实现低功耗温度传感器的关键[5].
低功耗数字滤波器一直是许多国内外学者的研究重点,Kilic等[6]开展了面向射频接收器的数字滤波器设计,提出了多种低功耗梳状滤波器架构;Chavan等[7]提出了一种用于调频连续波雷达收发器的数字滤波器,由级联积分梳状(cascade integrator comb,CIC)滤波器和半带滤波器级联而成,采用该结构可以有效降低数字滤波器的功耗;钱泽斌等[8]通过利用静态存储器来存放数字滤波器系数,并对多级数字滤波器进行耦合设计,极大地提高了时钟利用率,使功耗减小了60%,该滤波器应用于音频芯片.可以看出,低功耗数字滤波器的研究主要针对输入为中高速信号的情况,而对于输入为低速信号(如温度等)的情况研究较少.
为了降低温度传感器的功耗,本文开展了面向CMOS温度传感器的低功耗数字滤波器设计,完成了递归结构CIC滤波器和基于移位加法器的有限脉冲响应(finite impulse response,FIR)滤波器的硬件实现,通过分析滤波器精度与功耗之间的关系,提出了一种可根据精度需求变化自行调节运算单元数量的数字滤波器,有效降低了滤波器运行时功耗.此外,针对温度信号的变化特点,采用一种低功耗工作模式,并对这种工作模式下滤波器的运算方式进行优化,使滤波器功耗进一步降低.
1 CMOS温度传感器架构
本文提出的CMOS温度传感器由基于2阶调制器的前端电路和数字信号处理电路两部分组成,其架构如图1所示.环境温度经过基于双极晶体管(bipolar junction transistor,BJT)测温原理的感温电路产生用于比率计算的两个关键电压Vbe1和Vbe2.2阶Sigma-Delta(ΣΔ)调制器用于将感温电路产生的模拟电压量化为带有温度信息的数字比特流.
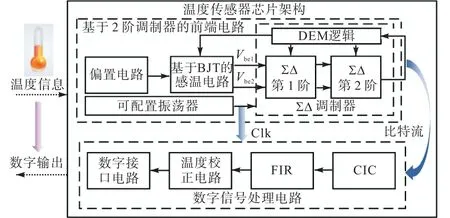
图1 CMOS温度传感器架构Fig.1 Architecture of CMOS temperature sensor
Sigma-Delta调制器输出的数字比特流在未经处理情况下并不利于用户直接获取温度信息,一是因为该信号在高频处存在的大量冗余噪声会影响信号质量;二是因为该信号工作频率较高,若不进行降采样处理,将极大增加后续数据处理工作量[9].因此,需要在调制器后设计数字滤波器电路去解决上述两个问题.数字滤波器通常分为单级结构和多级结构,单级结构容易设计,原理简单,但实现较好性能往往需要较大开销[10].为降低电路开销,本设计选取“CIC+ FIR”这种多级结构.
为了降低由温度漂移和自热效应所引入的测温误差,在数字滤波器后设计了温度校正电路,该电路可以根据不同温度区间内测温误差的不同进行分段温度校正,从而提升测温精度.数字接口电路通常由通信模块和功能逻辑模块组成,通信模块用于温度信息读取和功能逻辑电路的配置,功能逻辑电路则为用户提供了多种功能选择,实现了CMOS温度传感器的智能化.
2 数字滤波器电路的硬件实现
2.1 CIC滤波器电路
CIC滤波器是一种特殊的FIR滤波器,其特点是所有滤波器系数均为1,因此,在硬件实现过程中无需进行任何乘法运算,相比于需要大量运算才能完成滤波的FIR滤波器来说很大程度上降低了硬件开销,故常作为多级数字滤波器的第1级[11].CIC滤波器的传输函数为
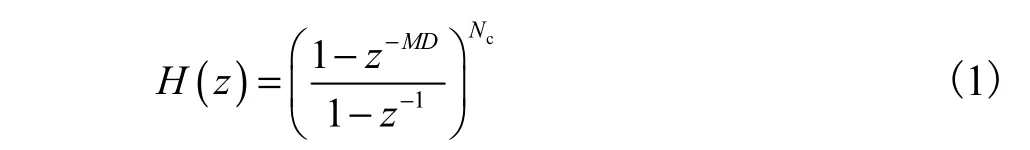
式中:M为差分延迟因子,一般设置为1;D为CIC滤波器阶数,通常由Sigma-Delta调制器的过采样率决定;Nc为CIC滤波器级数,通常由Sigma-Delta调制器的阶数决定,当前级调制器阶数为L时,为了保证温度传感器的测温精度,CIC滤波器级数一般需要L+1级[12].
假设L+1为3,3级D阶CIC滤波器的一般实现结构如图2(a)所示,可以看出信号先经过3级积分器,再经过3级差分器,最后完成D倍抽取.但这种结构往往功耗较高,一是该结构中各部分电路一直工作在一个较高频率下,二是在每一级差分器实现过 程中都需要D个延迟单元.因此,为降低传感器功耗,本设计采用一种递归型CIC滤波器的实现结构,如图2(b)所示,该结构由CIC滤波器一般实现结构经Nobel恒等变换而来,通过将差分器和抽取器位置对调,使信号在经过积分器后先经过抽取器再经过差分器,不仅使差分器工作在较低工作频率下,也减少了冗余运算和延迟单元的使用.
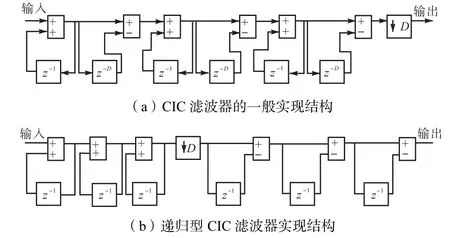
图2 CIC滤波器的实现结构Fig.2 Structure of CIC filter
2.2 FIR滤波器电路
FIR滤波器是数字滤波器的重要组成部分,通常级联在CIC滤波器后来进一步滤除信号的高频噪声,具有系数对称、通阻带边界易于控制等优点[13-14]. 对于Nf阶FIR滤波器,其传输函数为

式中h(n)为FIR滤波器系数.
FIR滤波器在硬件实现过程中应尽可能减少运算单元数量,以此来限制滤波运算过程中由逻辑翻转所引入的大量功耗.本设计根据FIR滤波器系数对称的特点,通过系数复用方式将运算单元数量减少一半.此外,将该结构中乘法器替换为移位加法器,使乘法运算转化为多个加法运算,从而实现进一步节省运算单元的目的.当Nf为奇数时,基于移位加法器(shift adder,SA)的Nf阶FIR滤波器的实现结构如图3所示,其中,n=(Nf-1)/2.
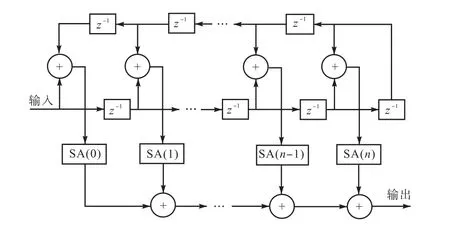
图3 基于SA的FIR滤波器的实现结构Fig.3 SA based structure of FIR filter
图3 中SA(n)单元复杂度直接取决于滤波器系数h(n),该系数量化后的二进制码中每多有一位是1,则需要额外设计一个移位寄存器和一个加法器. 为了简化量化后的系数,使用正则有符号数(canonic signed digit,CSD)码来代替普通二进制码对系数进行编码.CSD编码是一种基于权值{-10 1}的表示法,在该表示法中,不能有两个连续的非零位[15],如二进制码01101111,采用CSD码表示为10010001,可以看出,利用CSD编码比利用普通二进制编码具备更少的非零位,特别是系数中出现连续1的情况下效果更为突出,将有效地降低硬件资源.
为了验证所使用数字滤波器结构与传统数字滤波器结构的功耗优势,本节利用PTPX工具对两种滤波器结构进行了功耗仿真实验,实验相关配置如下:滤波器工作电压为1.62 V,滤波器工作频率为1 MHz,仿真时间为1 ms.根据仿真结果可知,相比于传统数字滤波器,本设计所使用的数字滤波器功耗降低了60.1%,其中,CIC滤波器部分功耗降低了82.5%,FIR滤波器部分功耗降低了10.9%.
3 数字滤波器电路的低功耗优化
3.1 精度自适应的数字滤波器
在数字集成电路硬件实现过程中,精度和功耗通常是一对不可兼得的指标,精度的提升往往意味着需要更多的功耗开销.对于数字滤波器电路来说,要想实现更好的滤波效果,必将需要更多的运算单元.
通过分析不同数字滤波器的幅频响应,可以得到影响数字滤波器精度的因素.多级CIC滤波器的幅频响应为
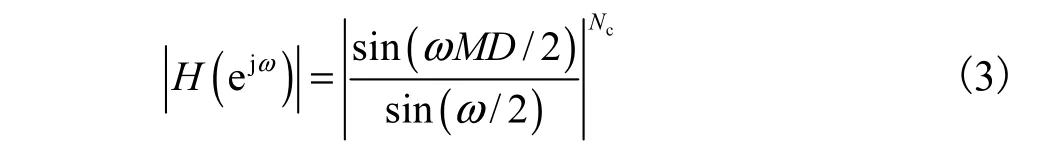
由式(3)可知,CIC滤波器的幅频响应主要由M、D和Nc3个参数决定,在本设计中M和D是固定参数,Nc为可变参数.通过控制每级CIC滤波器对应的运算单元,可以得到具备不同幅频响应的CIC滤波器.图4展示了不同级数CIC滤波器的幅频响应.
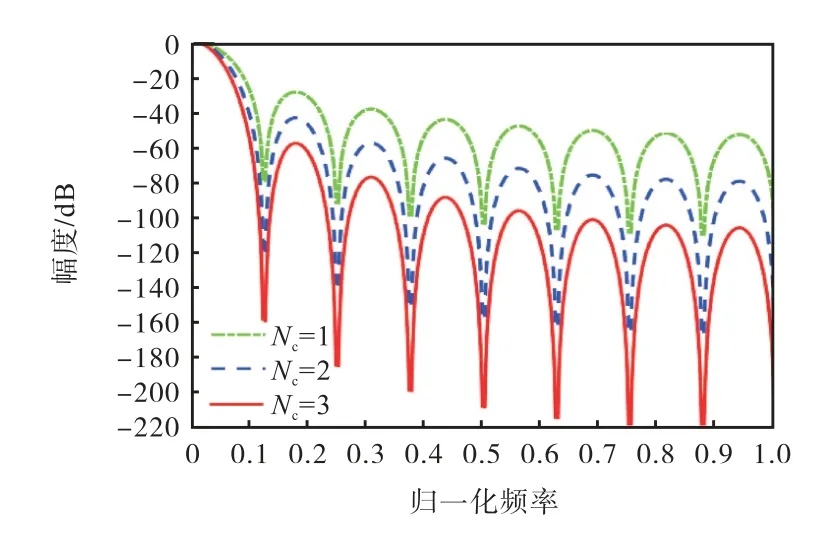
图4 不同级数CIC滤波器的幅频响应Fig.4 Amplitude-frequency responses of CIC filters with different levels
本设计使用的FIR滤波器系数是偶对称的,其幅频响应为
由式(4)可知,FIR滤波器的幅频响应主要由h(n)和Nf决定.在已设计的FIR滤波器基础上,通过对不同h(n)对应的运算单元进行关断,可以使FIR滤波器具备不同的幅频响应.图5展示了利用上述方法设计的不同阶数FIR滤波器的幅频响应.
由图4可以看出,CIC滤波器幅频响应随Nc改变而改变,由图5可以看出,FIR滤波器幅频响应随Nf改变而改变,基于此,可以通过调整CIC滤波器级数和FIR滤波器阶数来获得不同精度的数字滤波器.
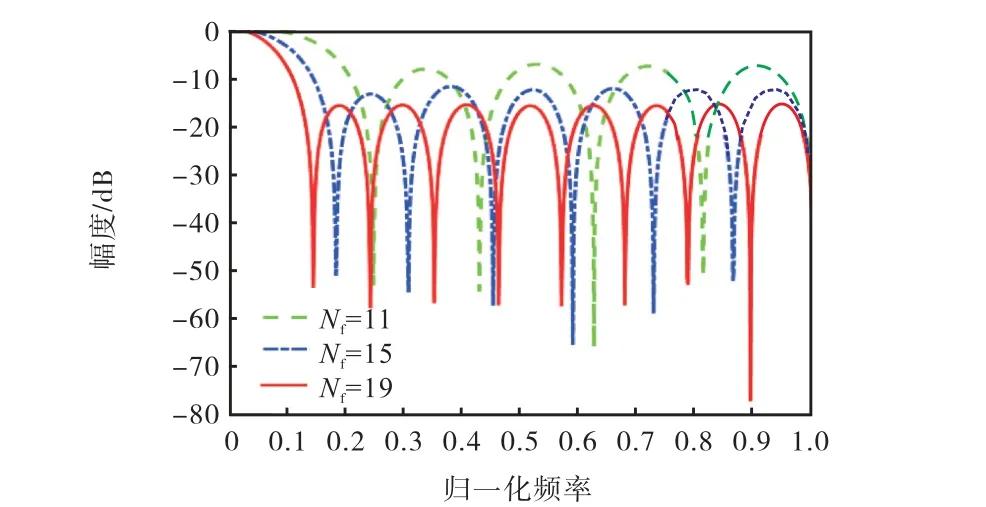
图5 不同阶数FIR滤波器的幅频响应Fig.5 Amplitude-frequency responses of FIR filters with different orders
温度报警是数字温度传感器中一个常见功能,当实测温度在用户设定阈值温度区间内时,传感器会给用户一个警示,以便用户根据当前温度做出相应调整.一般情况下,用户会更在意实测温度是否在阈值温度区间内,因此,当实测温度在阈值温度区间内时,用户对传感器精度要求较高,当实测温度在阈值温度区间外时,用户对传感器的精度要求就没有那么严格了,若依旧进行高精度温度监测,将引入许多不必要的功耗开销.针对这一问题,提出一种精度自适应的数字滤波器,其架构如图6所示,该滤波器可以根据实测温度与阈值温度区间差值自行调节滤波器精度,当滤波器精度要求不高时,精度自适应的数字滤波器会降低CIC滤波器级数和FIR滤波器阶数,从而降低滤波所需的运算单元数量,需要注意的是,该过程只对已有运算单元进行操作,并没有引入新的运算单元.基于上述原则,完成了精度自适应数字滤波器的硬件设计,该滤波器可具备4种精度模式,当实测温度处于阈值温度区间内时,滤波器具备最高精度,此时称滤波器处于状态A;当实测温度与阈值温度区间的差值小于X1时,滤波器具备次高精度,此时称滤波器处于状态B;当实测温度与阈值温度区间的差值大于X1小于X2时,滤波器具备次低精度,此时称滤波器处于状态C;当实测温度与阈值温度区间的差值大于X2时,滤波器具备最低精度,此时称滤波器处于状态D.其中,X1、X2和阈值温度区间均可利用数字接口进行配置,在默认配置下,X1为5℃,X2为10℃,阈值温度区间为0~25℃.
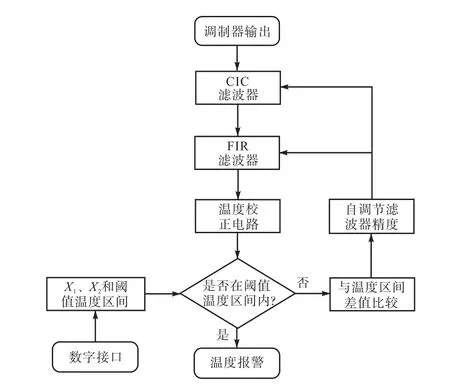
图6 精度自适应的数字滤波器架构Fig.6 Structure of a precision adaptive digital filter
3.2 低功耗工作模式
在自然界中,温度通常是变化缓慢的,若温度传感器对其进行频繁监测,实际上许多工作是不必要的.针对这一情况,使用了一种低功耗工作模式,在这种工作模式下,温度监测被分为单次温度转换(single temperature conversion,STC)阶段和闲时关断(idle shutdown,IS)阶段,这种低功耗工作模式的工作时序如图7所示.
图7中SD信号是优先级最高的信号,当SD信号为1时滤波器开始工作,当该信号被拉低为0时,滤波器立即停止工作,所有信号恢复到初始状态. CR_ctrl信号控制滤波器的工作模式Mode,当CR_ctrl信号为1时,Mode处于STC阶段,滤波器完成一次温度转换;反之,当CR_ctrl信号为0时,Mode处于IS阶段,滤波器停止温度转换.其中,STC阶段工作时长取决于数字滤波器级数和阶数,为固定参数;IS阶段时长则受数字接口电路控制,为可配置参数,该阶段时长越长,滤波器平均功耗将 越低.
图7下半部分为STC阶段的FIR滤波器工作时序,在该阶段,FIR滤波器需要CIC滤波器提供n个数据才能完成的滤波运算,本设计中n等于Nf.在FIR滤波器滤波运算过程中,每有一个输入数据Data_in进入,FIR滤波器就会输出一个累计和Add_sum,但是,只有n+1个数据均输入后所得到的Add_sum才是有效输出,其余的n次运算均为冗余操作.对于这些额外的运算,本设计使用En信号作为数据门控信号,关断A(0)~A(n-1)的运算,只开展A(n)的运算,并将其运算结果作为最终的数据输出.经功耗分析,提出的FIR滤波器优化方法使FIR滤波器工作在STC阶段时的功耗降低了5.5%.图8展示了优化前后FIR滤波器在STC阶段的功耗曲线,其中,图8(a)为整体功耗曲线,图8(b)为局部放大功耗曲线.为了更突出展示功耗改变,功耗仿真选用25 MHz时钟作为滤波器的工作频率,可以看出优化后滤波器功耗尖峰有明显的减少.
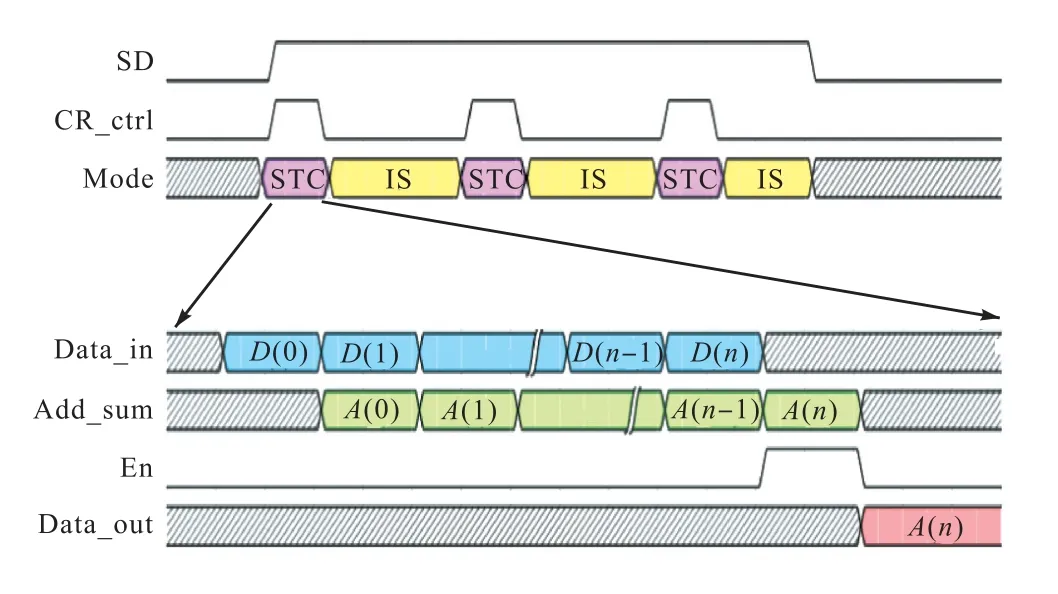
图7 低功耗工作模式的工作时序Fig.7 Work timing of the low-power mode
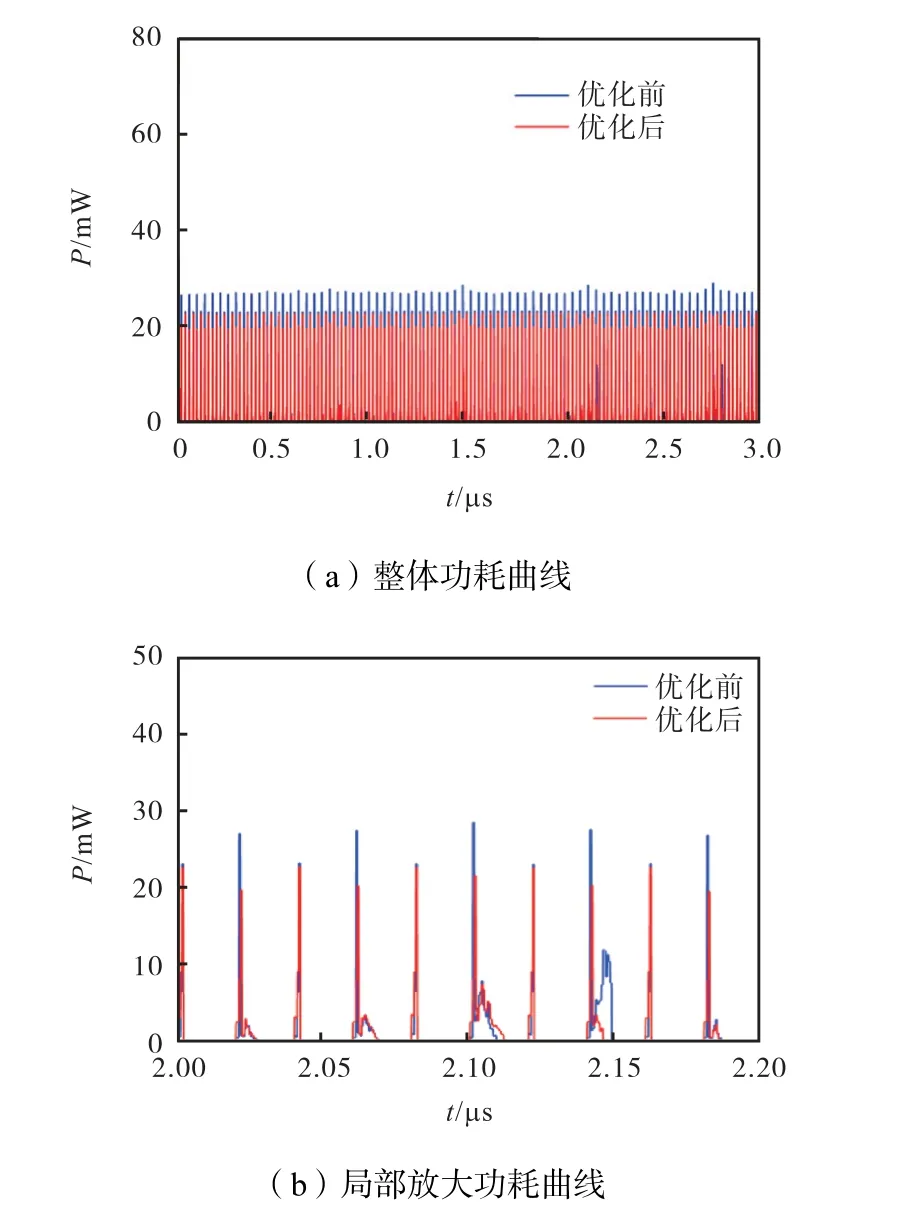
图8 FIR滤波器在STC阶段功耗Fig.8 Power consumption of the FIR filter at the STC stage
4 传感器芯片测试结果
温度传感器采用180 nm CMOS工艺完成流片,图9为温度的测试过程,其中,图9(a)为传感器芯片显微照片,图9(b)为芯片测试平台.

图9 温度传感器的测试过程Fig.9 Test process of the temperature sensor
为了验证所设计传感器的实际测温效果,将带有待测传感器和PT1000的测试板置于爱斯派克超低温试验箱ESPEC GMC-71中.在每一个温度值,使用单片机连续采集40次待测传感器的实测温度,利用高精度万用表读取每次单片机采集时的PT1000电阻值作为参考温度,通过分析40个实测温度与参考温度的最大差值,可以得到每个温度点待测传感器的测温精度.经测试,在-55~115℃温度区间内,传感器具备0.47℃测温精度,传感器优良的测温精度也说明数字滤波器具备不错的精度特性,图10展示了实测温度与测温误差绝对值|E|的关系.
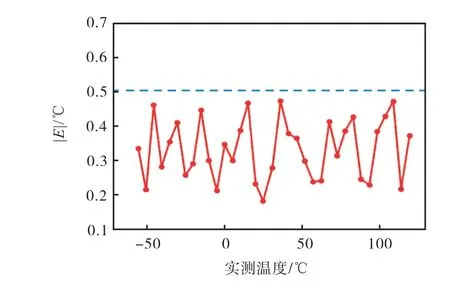
图10 温度传感器的精度Fig.10 Precision of the temperature sensor
利用数字接口电路写入不同的X1、X2和阈值温度区间,在精度自适应的数字滤波器作用下,传感器将具备不同的测温精度.图11分析了精度自适应数字滤波器的引入对传感器测温精度的影响,4条曲线分别代表了滤波器处于不同工作状态时传感器的测温精度.
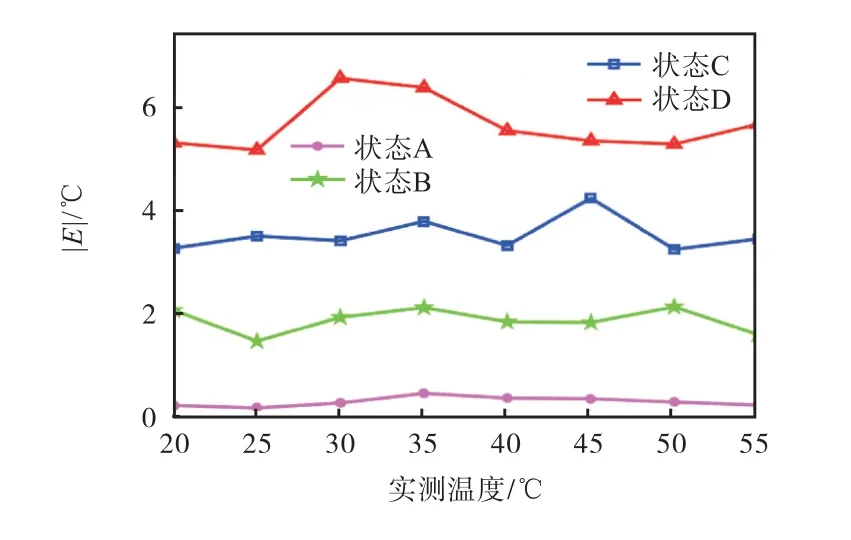
图11 不同状态下温度传感器的精度Fig.11 Precision of temperature sensors in different states
图12 为传感器数字部分在低功耗工作模式下的实测功耗曲线,曲线的高值为STC阶段功耗,低值为IS阶段功耗.在滤波器工作在状态A时,STC阶段功耗为71.55 μW,IS阶段功耗为20.12 μW,平均功耗为20.15 μW.当IS阶段时间要求比较严格时,精度自适应滤波器的引入将有效降低传感器数字部分的平均功耗,经测试,传感器数字部分处于状态D比处于状态A功耗降低11.3%.
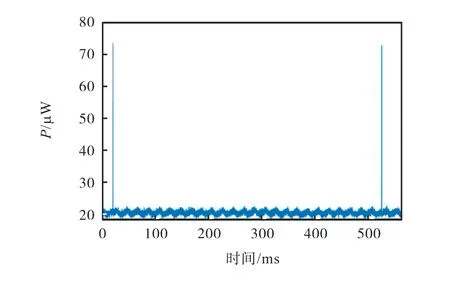
图12 温度传感器数字部分的功耗Fig.12 Power consumption of the digital part of the temperature sensor
5 结 语
本文基于180 nm CMOS工艺开展了面向CMOS温度传感器的低功耗数字滤波器设计,该滤波器采用递归型CIC滤波器级联基于SA的FIR滤波器的架构,相比于传统滤波器,功耗降低了60.1%.在该架构基础上,根据温度传感器的工作特点,进一步优化数字滤波器功耗.首先,提出一种精度自适应的数字滤波器,根据实测温度与设定阈值温度区间差值,调节滤波器运算单元数量,从而控制滤波器的功耗.其次,采用一种低功耗工作模式,将温度监测分为STC阶段和IS阶段.针对STC阶段只完成一次温度转换的情况,对FIR滤波器冗余运算进行关断,使FIR滤波器功耗降低5.5%.测试结果表明,当实测温度在阈值温度区间内时,传感器数字部分功耗为20.15 μW,在-55~115℃温 度 区 间 内,精 度 为0.47℃;当实测温度在阈值温度区间外时,传感器数字部分功耗最大可下降11.3%.

