连杆式差动平衡机构构型综合与优化设计
宋轶民 ,杨志岳,岳维亮,霍欣明,孙 涛,连宾宾
(1. 天津大学机构理论与装备设计教育部重点实验室,天津 300354;2. 天津仁爱学院机械工程系,天津 301636;3. 天津创智机器人科技有限公司,天津 300300)
随着社会需求不断增加,移动机器人开始在军事侦查、安防救援、环境监测、国土安全、空间探测等领域得到广泛应用[1-2],用以替代人类在高危场地、狭小空间、极端环境等场景中执行数据采集、样本回收、辅助操作等任务.
移动机器人在执行任务时通常面对复杂的非结构化环境,在移动过程中保持运动性能的优劣成为任务执行成功与否的关键,因此地形适应能力及运动稳定性成为机器人在特种环境下运动性能的重要评价准则.而移动机器人机身与行进结构(与地面直接接触的部分,如轮、腿、履带等)之间的连接方式对于其运动性能具有直接和重要的影响.
现有移动机器人机身与行进结构之间多为直接连接,仅允许行进结构绕驱动轴方向的转动,其转动中心在运动过程中始终位于同一平面内,在遇到非结构化地形时,无法始终保持与地面接触,容易发生倾覆.平衡摇臂悬架作为一种间接的连接方式,允许机身与行进结构之间相对调整,从而提升移动机器人的地形适应能力.差动平衡机构是平衡摇臂悬架的重要组成部分,起到了连接和调整的重要作用.差动平衡机构中应用广泛的主要有齿轮式和连杆式[3].齿轮式线性均化特性好、布局紧凑,但结构较为复杂、且占用机身内部空间.连杆式一般布置在机身外部,其运动空间位于机身外部,不占用机身内部空间,且便于拆卸,通过机构的合理设计可以实现良好的线性均化效果.陶建国等[4]设计了一种基于双闭环空间7连杆机构的差速平衡机构,并开展了理论分析和实验研究.Wettergreen等[5]提出的Scarab月球车和Amato等[6]提出的ORYX 2.0行星探测车均采用了连杆式差动悬架系统,用以实现对复杂地形的适应.程志红 等[7]提出了一种空间连杆式均角平衡机构,其对两侧悬架的摆角具有近似线性均化效果.Jiang等[8-9]和Gao等[10]提出了两侧均由空间RSSR四杆机构组成的连杆式悬架并将其应用在山地拖拉机中.目前,现有的连杆式差动平衡机构多来源于空间RSSR机构,仅在应用中调整了连杆的布置形式,且机构多布置在机身前方或后方,对机身的平衡有一定的影响.
构型综合方面,目前对空间机构构型综合的理论研究主要集中在并联机构,主要的构型综合方法有基于螺旋理论的综合法、基于位移子群/流形的综合法、基于方位特征集的综合法、GF集理论、虚拟链法、有限旋量综合法等[11-12],其中基于螺旋理论的综合法最为常见.现有综合方法大多适用于空间多环的并联机构,对空间单环机构的研究较少.郭盛等[13]根据不同的过约束组合对单闭环过约束机构进行构型综合.Kong等[14]采用将两个运动副插入多自由度单环机构的方法对变自由度单环机构进行构型综合.在连杆式差动平衡机构的构型设计方面,目前的研究大多只是根据经验进行设计,并未对其功能原理进行深入分析,缺乏对构型的系统研究.
本文针对上述问题,系统分析了连杆式差动平衡机构的运动特征及组成特点,概括了机构实现运动功能的基本条件,并基于螺旋理论,根据单侧机构公共约束数目和类型的不同综合得到可行的构型,从中优选出一种典型机构进行运动分析,以机构的运动和力传递效果为评价指标进行性能评价和参数优化设计,最后通过仿真展示了机构在移动机器人中的应用.
1 连杆式差动平衡机构的期望运动描述
连杆式差动平衡机构旨在通过两侧摇臂关于机身的相对摆动调整俯仰角以实现对不平地形的被动适应.为使两侧摇臂可以相对机身进行调整,两侧摇臂与机身之间应形成两共轴转动副(转动副以下简称R副).移动机器人在不平路面行走时,影响机构运动的主要因素为地形波动引起的两侧摇臂相对机身的摆动.在差动机构作用下,机身位姿由两侧摇臂与机身的相对位形确定,确定机构运动状态需施加的最少独立参数仅有一个,即摇臂和机身间的相对位置参数,因此机构的自由度为1.为保证机器人运动时,悬架对两侧地形具有相同的适应效果,机身俯仰角应为两侧摇臂摆角的均值,即两侧摇臂相对机身的转角应大小相等、方向相反,该特性即为悬架机构的均化特性.
通过上述分析,可得到连杆式差动平衡机构实现运动功能需要满足的基本条件:
(1) 差动平衡机构的自由度为1;
(2) 两侧摇臂与机身之间形成两共轴R副;
(3) 两侧摇臂关于机身的相对转角大小相等,方向相反.
由于两侧摇臂已通过两共轴R副与机身连接,当两侧摇臂状态确定时,机身仅有一转动自由度未被限定,因此差动平衡机构需要在两侧摇臂与机身之间建立运动链以约束机身的转动.考虑机器人机身两侧结构的运动平衡、均化特性保持及结构外观的合理性,两侧运动链设置为对称布置,两侧运动链与机身通过一个共用R副连接,机构可视为由两个组成相同、布置形式对称的单闭环机构组成,且单侧机构的自由度为1.
通过上述分析,将机构的综合问题简化为对单侧单自由度单闭环机构的构型综合,简化过程如图1所示.综合时首先考虑单侧机构,然后对称布置形成整体机构.考虑到机构外置于机身,直接面向服役环境,因此选择受外界温度、粉尘影响较小的 R副作为机构的组成运动关节.
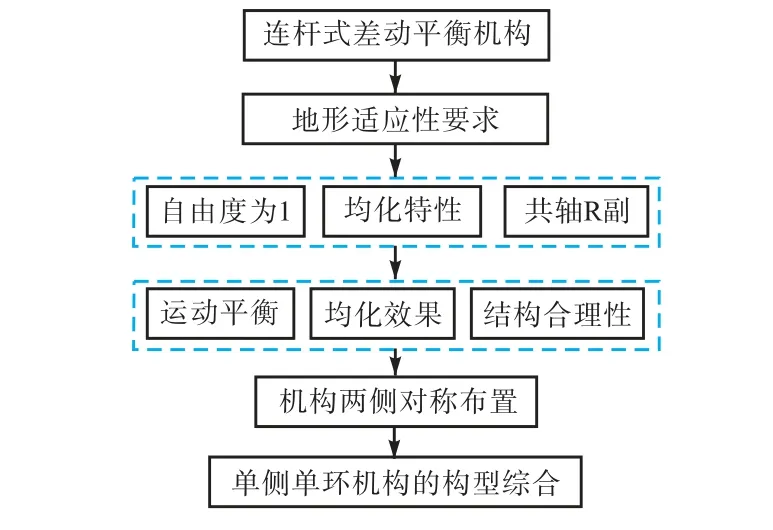
图1 机构构型综合简化过程示意Fig.1 Schematic of mechanism configuration synthesis simplification
本文结合螺旋理论[15],对含过约束和不含过约束且具有期望运动的单侧单自由度单环机构进行构型综合研究.综合得到可行的单自由度单环机构进行对称布置即可得到可行的连杆式差动平衡机构.
由修正的G-K公式[16]得
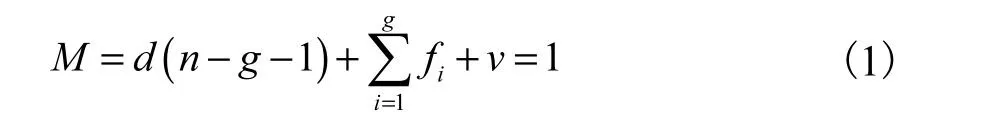
式中:M表示机构的自由度;d表示机构的阶数;n表示机构的构件数(包括机架);g表示运动副的个数;fi表示第i个运动副的自由度;ν表示冗余约束.对于单环机构,有ν=0,n =g.
由于构型综合时仅考虑R副,有 fi=1,故可得

式中d由公共约束数λ决定,d =6-λ.
不考虑构件数为3时,含有局部自由度的特殊机构[17].在单环机构仅含有R副时,其组成构件数目应至少为4,即 g≥4;由于机构的公共约束最小为0[12],即机构阶数不超过6,由式(2)可得 g≤7.此时,机构中含有的运动副数和对应具有的公共约束数包含以下情况
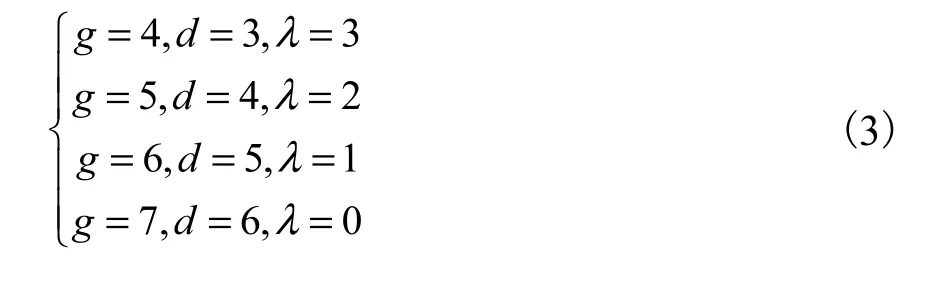
2 单侧机构的构型综合
2.1 运动螺旋与约束螺旋的几何关系
考虑机构两侧对称布置的位形要求和均化特性的运动要求,连接两侧机构的共用R副设置在两共轴R副中间且垂直于机身平面的位置.建立坐标系如图2所示,原点O位于机身中部,x轴和z轴分别沿共轴R副和共用R副,对于一侧的单环机构,两已知R副的运动螺旋可表示为
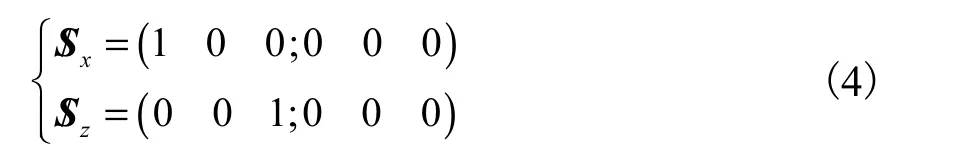
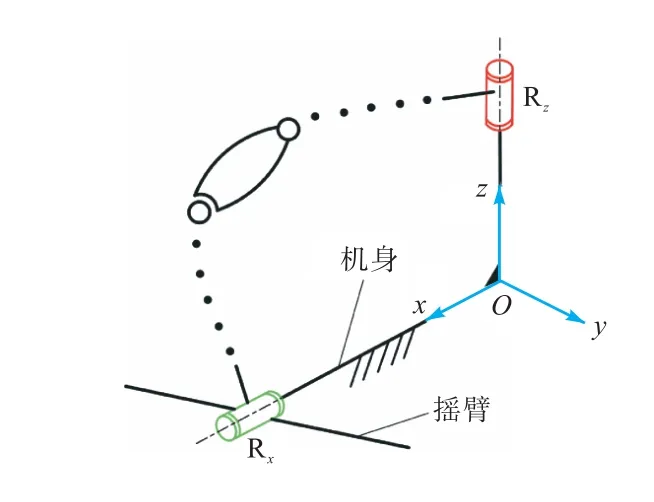
图2 连杆式差动平衡机构单侧机构组成示意Fig.2 Schematic of a single-side mechanism composition of linkage differential balance mechanism
设约束螺旋为 S/r=( lrmrnr;prqrrr),由运动螺旋与约束螺旋的互易积为0,可得
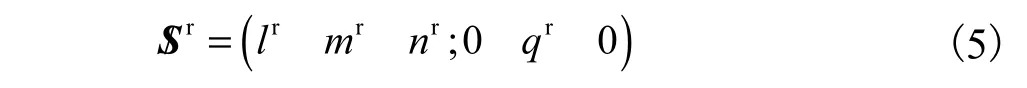
式(5)表明,单侧机构至多受到一个沿y轴方向的约束力偶的作用.由式(3)与式(5)可得该机构的阶数、运动副数、构件数及相应公共约束的可行组合,如表1所示.

表1 单侧机构的运动螺旋和约束螺旋组合Tab.1 Combination of motion and constraint screws of the single-side mechanism
将转动运动、约束力和约束力偶的螺旋表示为

式中ω、f及C分别表示转动角速度、力及力偶的 大小.
根据螺旋互易积运算规律[15],运动螺旋与约束螺旋互易积为0,可得

式中:a12和α12分别表示运动螺旋与约束力螺旋间的距离和夹角;α13表示运动螺旋和约束力偶螺旋间的夹角.
由式(6)可知,当运动为转动、约束螺旋为约束力时,有a12=0或 sinα12=0,即转动轴线与约束力相交或平行;由式(7)可知,当运动为转动、约束螺旋为约束力偶时,有 cosα13=0,即转动轴线与约束力偶 垂直.
2.2 含有公共约束的全铰链单环机构构型综合
结合表1所示分类,对含有不同数目和类型的公共约束的单环机构进行构型综合.
当机构的公共约束含有约束力时,约束力相互独立.由于两已知R副轴线交于点O,因此约束力至少与其中之一相交,此时存在3种情况:①约束力在Rx与Rz轴线确定的Oxz平面内,与Rx或Rz其中一轴线平行并与另一轴线相交;②约束力在Oxz平面内分别与两轴线相交于不同点;③约束力与Rx和Rz轴线交于点O.其中,情况①和②要求机构中含有的其他组成转动关节轴线处于或平行于平面Oxz,然而该瞬态几何关系难以在运动中保持,无法构成全周运动机构.因此,机构的约束力须过点O.当机构含有两个及以上约束力时,机构中含有的R副轴线须过点O.当公共约束中含有约束力偶时,由式(5)知约束力偶必沿y轴方向.
2.2.1 含有3个公共约束
1) 公共约束为3个约束力
此时机构共包含4个R副,且其运动轴线均经过点O,因此构成RxR1R2Rz机构,如图3(a)所示.在运动中R副的轴线特征保持不变,因此该机构运动具有全周性.由于R副在以O为球心的球面内运动,该类R副又称球面R副.
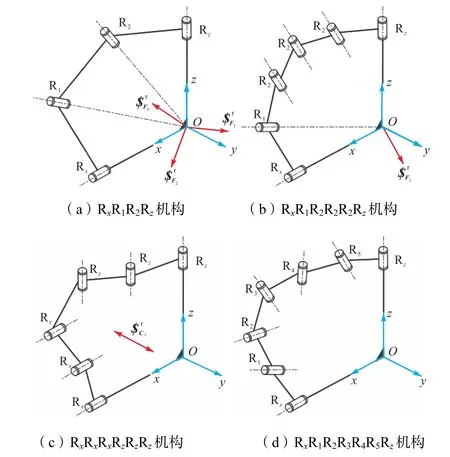
图3 几种典型的单侧机构Fig.3 Schematic of several typical single-side mechanisms
2) 公共约束为2个约束力和1个约束力偶
此时机构中的R副轴线应经过点O且与y轴方向垂直,即处于Oxz平面.然而在运动中上述瞬态几何关系无法保持,因此不存在全周运动机构.
2.2.2 含有2个公共约束
1) 公共约束为2个约束力
此时机构共包含5个R副,且其运动轴线均经过点O,因此构成RxR1R2R3Rz机构.然而,经分析可知该机构具有3个公共约束力,由G-K公式求得其自由度数目为2,不符合本文的构型综合需求.
2) 公共约束为1个约束力和1个约束力偶
此时机构中的R副轴线须与y轴垂直,且与约束力相交.上述瞬态几何关系无法在运动中保持,因此不存在全周运动机构.
2.2.3 含有1个公共约束
1) 公共约束为1个约束力
此时机构中的R副可分为两类:①R副轴线始终过点O,即球面R副;②R副轴线互相平行且始终平行于约束力,即平行R副.因此由表1可获得RxRxRxR1R2Rz、RxR1R1R1R2Rz、RxR1R2R2R2Rz(如图3(b)所示)和RxR1R2RzRzRz机构.在机构运动中上述几何条件保持不变,因此均为全周运动机构.其中,RxRxRxR1R2Rz、RxR1R2RzRzRz机构与RxR1R2Rz机构具有相同的运动形式.
2) 公共约束为1个约束力偶
此时机构中的R副轴线均与y轴垂直,因此构成RxRxRxRzRzRz机构,如图3(c)所示.该机构在运动中R副轴线始终处于或平行于Oxz平面,因此为全周运动机构.
综上所述,当机构包含公共约束时,共有6种可行的全铰链单环机构.
2.3 不含公共约束的全铰链单环机构构型综合
当机构无公共约束时,共包含7个R副,其运动螺旋系可描述为矩阵形式

由于不存在反螺旋,则该矩阵的秩为6.因此须存在3个轴线方向向量线性无关的R副.换言之,平行R副的组数最多为4组,其组合形式如表2所示. 考虑机构的运动特点,其首末R副不应为冗余关节.因此,当平行R副组数之和为4时,平行R副的组合形式应为RxRxRx和RzRzRz.

表2 平行R副的组合情况Tab.2 Combination of parallel revolute pairs
根据机构中含有的平行R副组数以及组合形式,可综合出39种可行的全铰链单环机构,如表3所示.需要指出的是,本文综合出的构型包含已有连杆式差动平衡机构中的RSSR机构.如将其中的RxR1R2R3R4R5Rz机构(如图3(d)所示)中的R1R2R3替换为S副,将R4R5替换为U副,即可得到RxSURz机构;如在S副与U副中间添加一个局部自由度,即可得到RxSSRz机构;考虑首末转动副轴线的一般 情况,即为现有连杆式差动平衡机构中采用的RSSR机构[4-10].

表3 不含公共约束时的可行机构Tab.3 Feasible mechanisms without public constraints
2.4 机构构型的选择
连杆式差动平衡机构在构型优选时,应结合其应用场景从结构复杂度、机构布置方式对机器人运动的影响程度以及制造难度和装配精度等方面考虑.为降低机构的复杂程度和制造装配难度,应尽量选择杆数较少的机构;从R副类型来看,由于球面R副的运动空间为球面,在运动过程中易与机身或其他零部件产生干涉,因此应尽量选择不含球面R副的机构.综合以上依据,本文选择含有一个公共约束的RxRxRxRzRzRz机构为目标机构,该机构的两组R副分别处于平行于机身和摇臂的两个平面,在运动过程中不会与其他零部件发生干涉.
3 机构的运动学分析
3.1 单侧机构的位置正解
由于RxRxRxRzRzRz机构中间的两个运动副RxRz可用U 副的进行替换,且考虑到机构布局的紧凑性,本文选择典型的RxRxURzRz机构进行分析.
建立坐标系Oxyz如图4所示,两侧单环机构关于Oyz平面对称布置,设连杆J1K1、K1L1、L1M1、M1N的长度分别为l1、l2、l3、l4,其与z轴或x轴方向的夹角分别为α1、α2、α3、α4,夹角的正方向由右手定则判定,机身高度和宽度方向尺寸ON和OJ1分别为h和b,则可得到各铰链中心点的坐标为:J1( b, 0,0);;

图4 RxRxURzRz型机构的运动简图Fig.4 Kinematic diagram of the RxRxURzRz mechanism
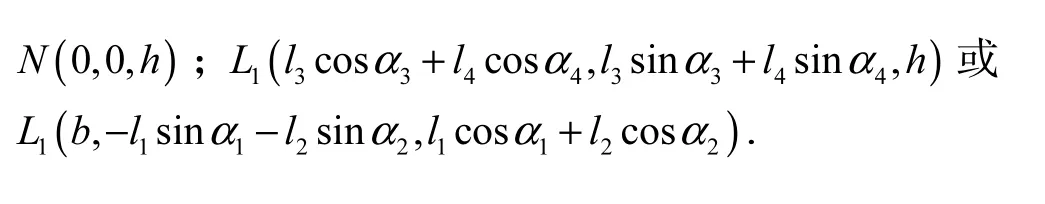
由闭环矢量方程
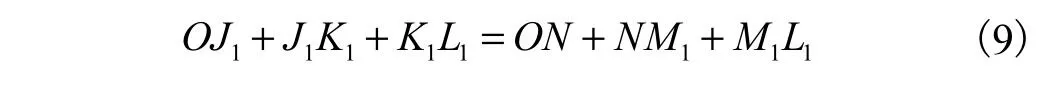
可得
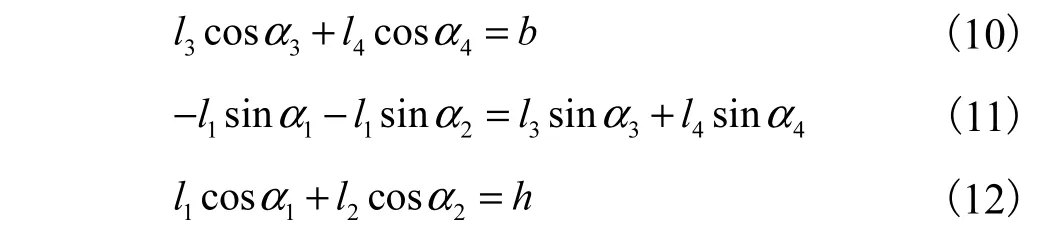
由式(12)可得

由式(10)、式(11)联立得

可解得

式中±可由运动连续性条件确定,本文在分析时取+.
将式(15)代入式(10)中,可得

3.2 单侧机构的位置逆解
与位置正解的求解方式类似,通过对闭环矢量方程得到的式(10)~式(12)进行变换,可得单侧机构的位置逆解模型如下.
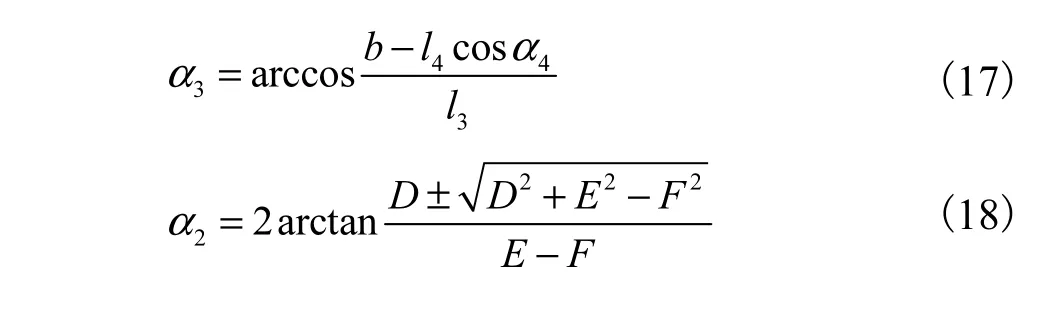

3.3 机构的奇异性分析
由于机构两侧对称布置,当一侧处于奇异位型时,整个机构也处于奇异位型,当一侧机构运动至J1、K1、L13点共线时,机构处于第1种奇异位型,此时有α1=α2,代入式(12),可得

当机构运动至L1、M1、N 3点共线时,机构处于第2种奇异位型,此时有α3=α4,代入式(10)~式(12),可得

由上述方程组可得
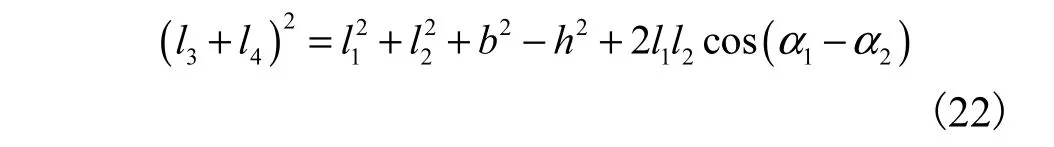
考虑到机器人摇臂在最大摆角处机构将处于第1种奇异位型,为使机构在最大摆角范围内避免出现奇异,第2个奇异位型应该在机构的摆角范围之外,即机构连杆长度须满足下式

4 机构的性能评价与优化设计
4.1 机构的性能评价
连杆式差动平衡机构主要起到连接和差动调整的作用,其运动可视为一侧摇臂的转动通过中间共用的连杆构件的转动向另一侧传递.因此,运动和力传递效果是机构性能的重要评价指标.刘辛军等[18]提出的运动/力传递特性指标有效评价了机构的运动和力传递性能,本文借鉴该评价指标,以螺旋理论为工具建立连杆式差动平衡机构的运动学性能分析模型,对机构的尺度参数进行优化设计.
将连杆式差动平衡机构的单侧机构拆解为两个支链RxRxURz和Rz,其中前者将摇臂的输入运动(地形波动)传递至运动输出构件——连架杆M1N(M2),后者则约束连架杆M1N(M2)只能绕z轴转动.
首先分析机构的输入传递指标和输出传递指标,如图5所示,对于支链RxRxURz,各运动副螺旋可表示为

图5 单侧机构运动螺旋示意Fig.5 Schematic of single-side mechanism’s motion screw

上述5个运动螺旋之间线性无关,因此该支链为一个5自由度支链,其运动螺旋系为螺旋五系.
由运动螺旋与力螺旋的互易积为0,得

可得支链约束螺旋 S/r=( 00 0;01 0).
以机构中摇臂端的摆动为输入运动,两侧单环机构共用连杆的转动为输出运动,则输入运动螺旋和输出运动螺旋可表示为
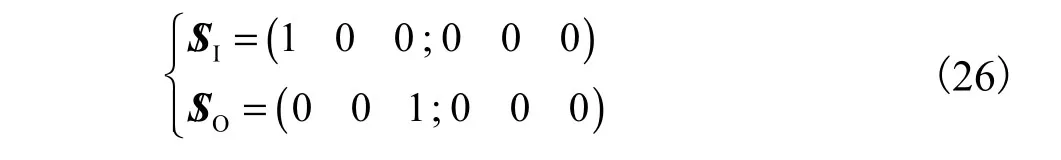
假定摇臂端Rx副被锁住,此时运动螺旋系变为螺旋四系.
由运动螺旋与力螺旋的互易积为0,得
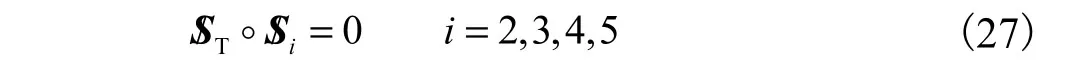
可得该支链的传递力螺旋为

式 中:pT=l1( cosα1tanα2-sinα1);rT=l4tanα2(cosα4- cotα3sinα4).
机构传递力螺旋与输入运动螺旋的互易积为

传递力螺旋与输出运动螺旋的互易积为

则机构的输入传递指标可表示为
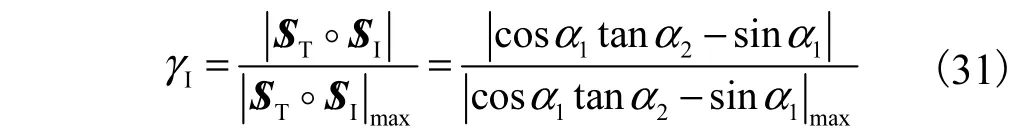
机构的输出传递指标可表示为

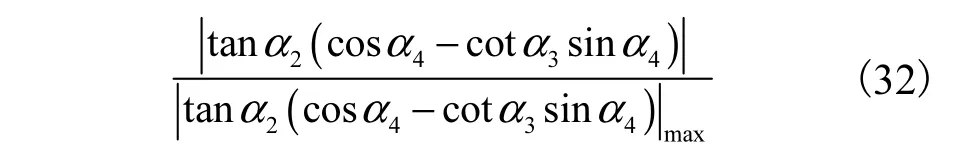
分别定义机构的全局输入传递指标和全局输出传递指标为

4.2 机构的尺度参数优化
以移动机器人的横向参数即OJ1的尺寸b为参考对机构中的其他参数进行无量纲化处理,则机构的尺度设计参数可表示为

考虑机器人实际应用场景中非对称地形左右两侧的地形波动程度,设定摇臂摆角范围为( -45°, 45°),且在α1=45°的边界位置处,机构处于第1种奇异位型,则由式(20)、式(23)可得

式中参数λ0= h b定义为连杆式差动平衡机构的高宽比,其与机器人的机身宽度和机身高度有关,不失一般性,考虑机器人机身内部的负载情况和外观的合理性,给定高宽比λ0= 0.53.优化时以λ1、λ3、λ4为独立设计变量,λ2为非独立设计变量.给定设计参数的上、下界分别为

机构的输入传递指标仅与设计参数λ1有关,因此首先根据输入传递指标优化设计参数λ1.全局输入传递指标在参数设计空间中的分布情况如图6所示,取设计参数λ1= 0.2723,此时全局输入传递指标取得最大值Γ1=0.7281.

图6 设计空间内的全局输入传递指标Fig.6 Global input transmission index in design space
将设计参数λ1= 0.2723代入式(32),可得机构的输出传递指标,全局输出传递指标在参数设计空间中的分布情况如图7所示,该值越大表示机构输出端的整体运动和力传递效果越好;Γ2的范围可以根据实际的工作需求选择,不失一般性,本文定义 Γ2≥0.85时为机构的优质输出传递区间.考虑加工与装配要求和工程应用条件,连杆之间的尺寸不宜相差过大,且为减小机构的整体质量,连杆长度之和应尽量小,故本文选择设计参数λ3= 0.6、λ4= 0.6667,此时对应机构的全局输出传递指标为 Γ2=0.8650.

图7 设计空间内的全局输出传递指标Fig.7 Global output transmission index in design space
设计参数确定后,可得机构在摇臂摆角范围内的输入和输出传递指标变化曲线如图8所示.

图8 γI和γO在摇臂摆角范围内的变化曲线Fig.8 Variation curves of γI and γO within the swing angle range of the rocker arm
5 仿真分析
考虑移动机器人的任务需求,给定机器人的宽度尺寸 b =150 mm,则可得到连杆式差动平衡机构的尺寸参数l1=40.8 mm、l2=72.3 mm、l3=90 mm、l4=100 mm .为验证选择的连杆式差动平衡机构在移动机器人地形适应性方面发挥的作用,基于本文提出的连杆式差动平衡机构,建立移动机器人的虚拟样机模型,其车轮半径设定为 R= 60mm ,车轮质心与其几何中心重合.利用ADAMS软件对移动机器人在复杂非对称地形的移动效果进行仿真分析.设定车轮转速为ω= 360°s ,仿真过程如图9所示,可以看到,采用本文选择的连杆式差动平衡机构的移动机器人可以顺利通过复杂的非对称地形,其应用效果得到验证.

图9 非对称地形仿真示意Fig.9 Schematic of asymmetric terrain simulation
为验证所选择的连杆式差动平衡机构的被动调整效果,测量移动机器人车轮质心在Z方向高度的波动曲线.前进方向右侧的车轮1和车轮4的质心高度波动曲线与其地形波动曲线如图10所示,左侧的车轮2和车轮3的质心高度波动曲线与其地形波动曲线如图11所示,可以看出车轮的质心高度波动曲线与地形波动曲线基本一致,且其差值为车轮的半径参数,由此可知,移动机器人在通过复杂的非对称地形时,车轮可以始终与地面保持良好的接触,从而验证了机构的被动调整能力,同时表明了采用该机构的移动机器人具有良好的地形适应能力.

图10 右侧车轮质心高度波动Fig.10 Fluctuation curve of right wheel centroid height

图11 左侧车轮质心高度波动Fig.11 Fluctuation curve of left wheel centroid height
仿真过程中,两侧摇臂及机身俯仰角的变化曲线如图12所示,其中θ1和θ2分别为摇臂1和摇臂2的俯仰角,θ3为机身的俯仰角.由图12可知,在移动机器人移动过程中,机身波动幅度明显小于两侧摇臂的波动幅度,且θ3为θ1和θ2的算术平均值,表明机构具有良好的均化效果.同时,采用该机构时,移动机器人机身的波动减小,从而能够提高其运动稳定性.
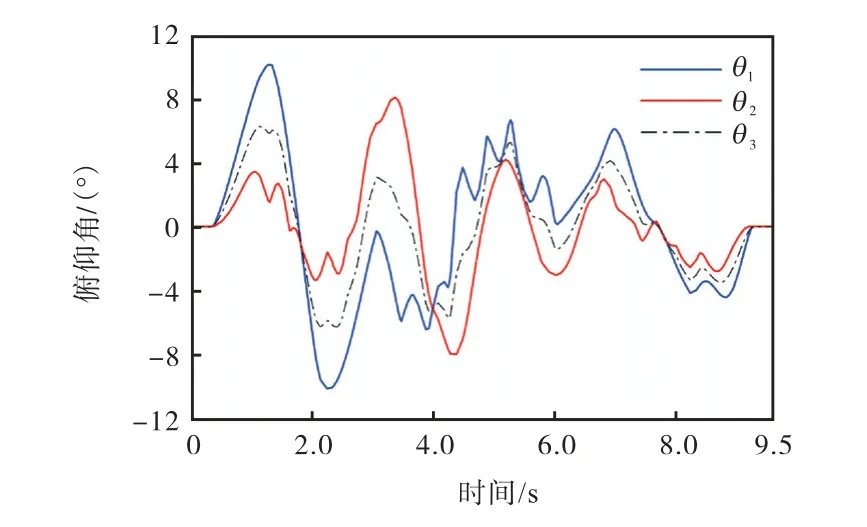
图12 摇臂和机身的俯仰角变化Fig.12 Pitching angle curves of rocker arms and fuselage
将机构锁定,即车轮直接与机身连接时,在同样的地形环境中进行仿真,可以发现移动机器人只有 3个车轮与地面接触,有一个车轮处于悬空状态,进而导致机器人运动不稳定.因此与直接连接相比采用本文提出的差动平衡机构,移动机器人可以具备更好的地形适应能力和运动稳定性.
6 结论
针对现有应用于移动机器人中的连杆式差动平衡机构构型单一、运动特征阐述模糊的不足,本文概括了连杆式差动平衡机构的运动特点,并结合螺旋理论对仅含有R副的连杆式差动平衡机构进行了构型综合研究,并优选出一种机构进行了运动分析、性能评价和优化设计,最后建立虚拟样机模型进行了仿真分析,全文结论总结如下.
(1) 总结了连杆式差动平衡机构的运动特征,概括了机构实现运动功能的基本条件.将机构的综合简化为对单侧空间单自由度单环机构的构型综合.结合修正的G-K公式和螺旋理论,根据机构含有公共约束的数目进行分类综合,得到可行的机构构型45种.从结构复杂度、机构布置方式对机器人运动的影响程度以及制造难度和装配精度等方面进行比较,优选得到典型的RxRxURzRz机构.
(2) 建立了RxRxURzRz机构的运动学模型,对机构进行了位置正逆解分析,并讨论了机构在运动过程中的奇异位型.以机构运动/力传递特性为评价指标,利用螺旋理论建立了机构的运动学性能分析模型,并对机构的尺度参数进行了优化设计,机构在优化参数下的全局输入和输出传递指标分别可以达到0.7281和0.8650.
(3) 结合任务需求,基于本文提出的连杆式差动平衡机构,建立移动机器人样机模型,利用ADAMS软件对移动机器人在复杂非对称地形的移动效果进行仿真分析.仿真结果表明移动机器人具备良好的地形适应能力和运动稳定性,分析结果验证了机构功能的有效性.

