基于信息-电力混合熵的边缘计算节点部署规划方法
季 浩 ,杨 挺,刘宇哲,耿毅男,张 东,李 炜
(1. 天津大学电气自动化与信息工程学院,天津 300072;2. 国网天津市电力公司,天津 300010;3. 国网冀北电力有限公司廊坊供电公司,廊坊 065000;4. 悉尼大学分布式高性能计算中心,悉尼 2006)
现代通信信息技术快速发展以及其与电力系统的深度融合,使得现行配电网已成为信息物理相互耦合的复杂系统[1-2].在配电信息物理系统(cyber physical distribution system,CPDS)中,分布式能源并网状态监控、继电保护装置投切、用户智能电表量测等物理设备和用户需求更加复杂多样,传统依靠单一云主站的集中计算处理模式存在着海量汇聚数据流传输高时延高拥塞、信息远离设备端且排队处理缓慢等弊端,难以完全支撑智能配电系统的实时高效信息分析、处理和决策需求[3-5].
边缘计算技术将计算力部署在近配电终端物理设备和数据源侧,可在控制执行单元侧进行数据分析、系统运行状态态势感知、并做出自主快速决策,可有效提升CPDS本地实时分析、计算、控制能力[5],满足系统快速反应需求,进而更好支撑CPDS系统 网络化最优控制运行,提升系统运行稳定性以及经 济性[6-9].
现有面向配电信息物理系统边缘计算部署规划的相关研究还较少,目前针对CPDS的规划研究多是从网络层面展开讨论,但涉及边缘计算节点优化部署方法的研究仍处于起步阶段.如文献[10]基于配电网多智能体参数一致性以电力信息投入成本最小化为规划目标,进行配网信息物理耦合规划;文献[11]通过分析CPDS的网元异构性,采用拓扑势均衡理论进行配电信息物理系统网络拓扑优化.此外,文献[12]采用双层规划模型对配电网储能位置和通信网络拓扑进行协同规划;文献[13]考虑了信息子系统随机故障对配电网电压控制的影响提出了一种信息物理耦合光伏电站规划.
然而上述配电信息物理系统研究中均没有涉及边缘计算节点(edge computing node,ECN)的优化部署这一特殊问题.
(1) 首先,ECN有别于普通的信息终端或传感器,是区域的核心枢纽节点,其担负本区域内信息的汇聚、分析和计算功能.因此,ECN在CPDS信息空间中的部署位置不同将直接影响数据流汇聚传输的稳定度和获取信息表达准确度(如受到传输延时、误码、丢包等影响).
(2) 由于CPDS系统中的电力物理子网与信息子网紧耦合相互依存关系,电力物理节点的稳定度同样作用于边缘计算节点,进而会通过ECN对自治区域的实时控制决策过程反馈回电力物理子系统,影响系统运行.
因此从信息稳定度和电力稳定度双层面分析,优化部署ECN,对面向边缘计算新模式的CPDS系统有重要意义.
针对上述问题,本文研究并提出一种边缘计算节点优化部署规划新方法.算法通过建立CPDS网络信息传输稳定度计算模型、电力稳定度计算模型和CPDS信息-电力混合熵计算模型,基于熵最大原理实现对CPDS网络边缘计算节点的最优化部署求解.本文以IEEE39节点标准算例进行仿真实验验证,从系统运行异常状态上报传输时延、网络吞吐量以及系统频率稳定控制性能实验判定方法性能.结果表明基于混合熵的边缘计算节点优化部署规划方法能够有效提升对网络状态获取时效性,并实现对CPDS快速响应控制,保障网络可靠性.
1 基于信息-电力混合熵的边缘计算节点部署规划模型
基于边缘计算自治域划分,在每个分区内进行端到端的信息稳定度计算和电气稳定度计算,从而建立CPDS信息-电力混合熵模型.
1.1 CPDS网络信息稳定度计算模型
CPDS网络需满足各终端设备与边缘计算节点间信息传输满足实时性、准确性和完整性,以保证配电系统正确的状态估计和运行稳定控制.而ECN作为自治域内信息流汇聚和高效处理节点,其部署位置必须考虑本区域内数据传输的稳定性.因此,本文计及信道环境和传输路径,选择时延、误码和丢包3个方面QoS属性进行端到端的信息稳定性标度λcyb分析.其包含信息终端间,如远程终端(remote terminal unit,RTU)或数传终端(data transfer unit,DTU),信息实时度λdelay、信息准确度λerror和信息完整度λloss. 并计算信息传输稳定度,其数学计算表达式为
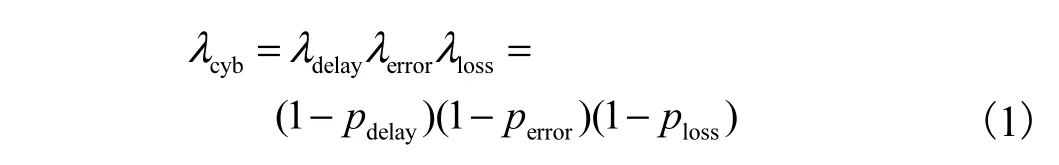
式中pdelay、perror和ploss分别为相应的传输时延、误码、丢包的数学量化概率数值.
(1) 信息实时度:在CPDS网络中,通信延时主要受到网络负载率和路由转发跳数的影响.基于网络流理论,可将汇聚网络流的端到端的时延概率分布近似为Pareto分布模型[14],则端到端时延概率分析模型为
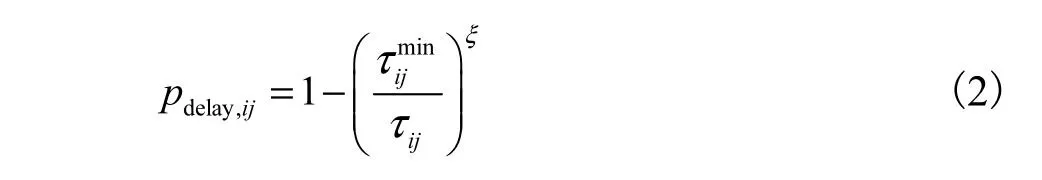
(2) 信息准确度:数据在终端设备与边缘节点间
传输时,因其信道特性和外界环境作用会产生误码.致使部分信息错误,降低传输表达准确度.误码率与链路信噪比和数据调制方式有关[15],具体计算表达式为
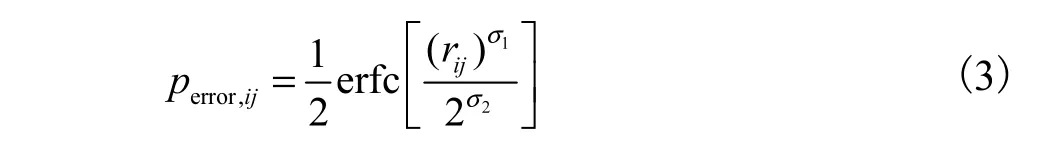
式中:rij为节点i与j间通信链路信噪比,取值为服从正态分布的随机数;,为互补误差函数,其中参数σ1、σ2与数据调制方式相关(如QPSK数字调制).
(3) 信息完整度:考虑到CPDS网络中网络环境和网络设备的特异性,则网络丢包率难以由通信参数进行数学建模表示.但在网络端到端传输的丢包事件间存在短相关性,因此可基于此特性采用两状态马尔可夫模型(即Gilbert模型)对CPDS网络丢包状态进行建模,即
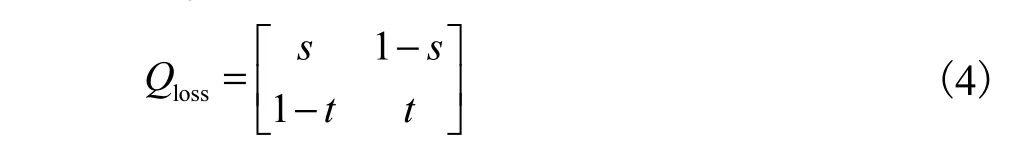
式中:Qloss为丢包模型状态转移矩阵;1-s表示由正常收包状态转为丢包状态的概率;1-t表示由自由丢包状态转为收包状态的概率.
令随机变量Y1和Y2分别为CPDS网络中突发性丢包长度与连续性无错收包长度,其概率函数分别为
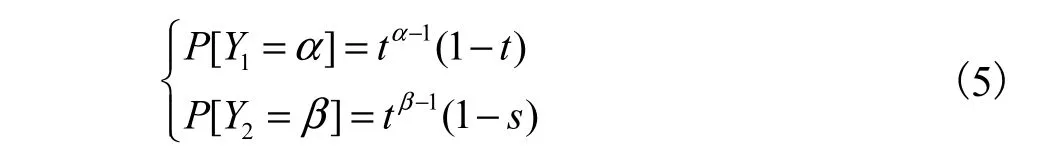
则由两者期望函数可得CPDS网络中丢包率为
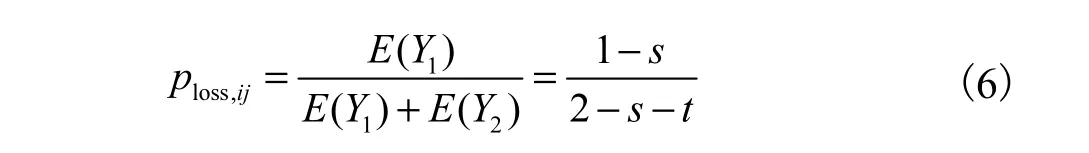
1.2 CPDS网络电力稳定度模型
除考虑CPDS网络信息稳定性模型外,ECN部署还需考虑电力系统一次侧的电力稳定性.稳定可靠的电力节点可更好地支撑边缘计算节点运行,减小因电力物理节点失稳造成耦合的信息子系统ECN性能损失,避免形成全自治域的控制功能丧失,并波及互联邻域.
在此采用量化CPDS网络物理节点受扰后的小干扰电压变化观测方法,建立节点电力稳定性标 度λphy.
在配电网稳定运行状态下,通过在系统中增加小干扰,如改变负荷,基于潮流计算可获得节点i的电压增量ΔUi为
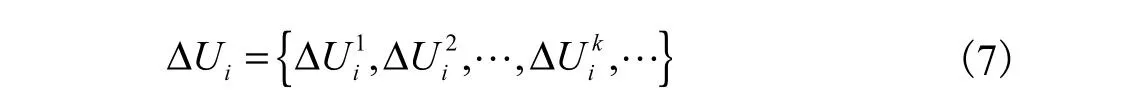
进而定义节点i受节点k扰动后电压偏移量与电压裕度之比的最大值为该节点脆弱性标度pi,其数值越大,说明节点受扰后越脆弱,计算式为
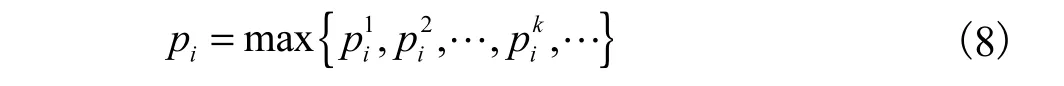
其中
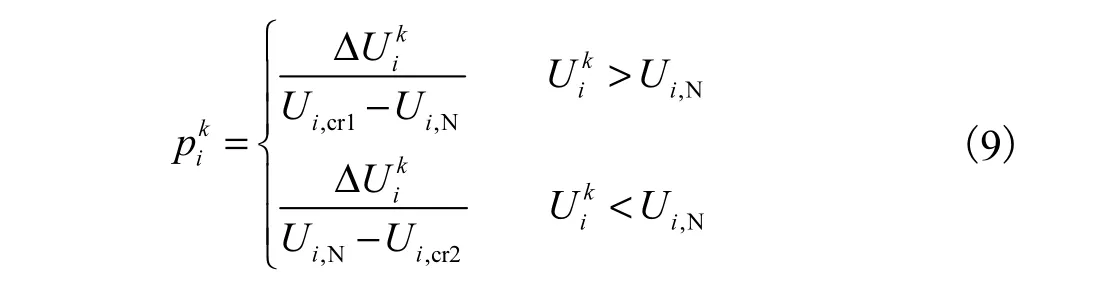
式中Ui,cr1与Ui,cr2分别为节点i电压上、下临界值.
则节点i电力稳定性标度λphy,i与信息稳定度形式一致,计算式为

1.3 边缘节点部署规划模型
基于上述CPDS网络信息稳定度计算模型和电力稳定度计算模型,可得到CPDS网络信息-电力稳定度公式为
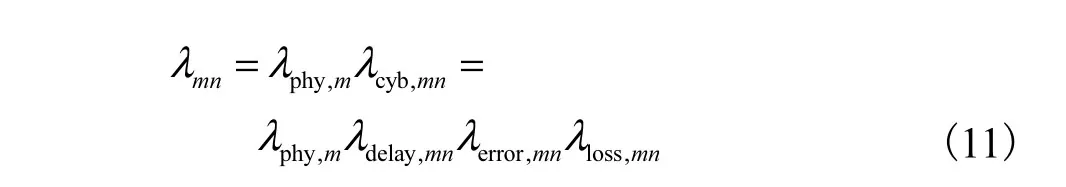
式中λmn为CPDS网络中边缘计算节点m与终端设备n间的信息-电力稳定度.进而基于λmn计算信息-电力混合熵,形成CPDS边缘节点部署规划模型.
熵是物理学中状态函数,是具有加和性的广度量非守恒量,可用于系统稳定性判定.一个系统中的随机状态量越是接近,熵值越大,则说明该系统稳定性越强.本文基于此特性构建基于信息-电力混合熵的CPDS边缘节点优化部署模型.问题建模的目标函数为
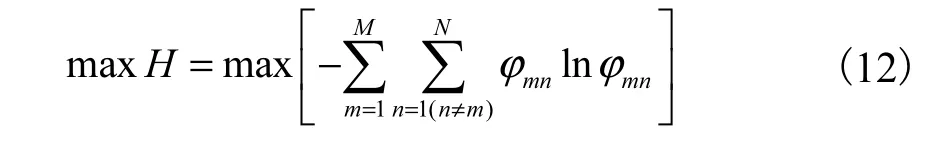
规划模型约束条件为
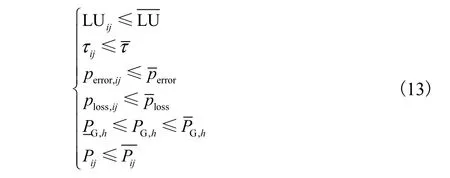
模型约束集分别从信息与电力两方面设立,其中信息层面的约束为链路利用率、时延、误码率和丢包率约束,均不能违背各自的阈值上限;电力物理层面约束是在进行电力潮流计算所涉及的参数规约,其考虑机组出力与支路潮流约束,其中PG,h为发电机组h的有功出力值,和分别为机组h出力上、下限,而支路潮流Pij限制约束则维持在限制范围内.
2 基于二进制粒子群算法求解模型
第1.3节所建立的配电信息物理系统边缘节点部署优化问题模型为非线性单目标规划问题.自变量为边缘计算节点ECN的最优放置,即备选点是否配置.因此可将其映射为二进制0~1整数规划问题,其中1表示配置ECN.
本文采用二进制粒子群算法求解该优化问题.设置该问题的适应函数为
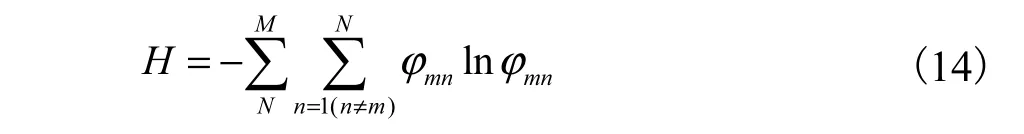
在各粒子的速度更新公式中采用转换限制函数sig(·)将速度值映射在区间[0,1]中,则有
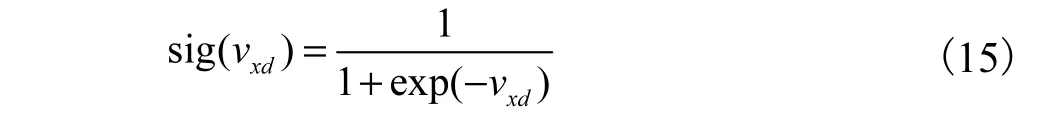
进而得到二进制粒子群算法的位置和速度更新公式分别为
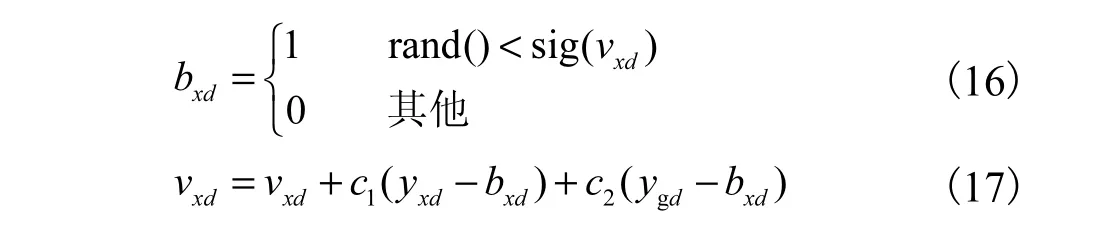
式中:bxd为粒子x在d时刻的飞行位置,即用0或1表示可能的部署方案;vxd表示粒子x在d时刻的飞行速度,即表示该点部署边缘计算节点的概率;yxd和ygd分别为粒子x和种群的历史最优位置;c1和c2为常数,取值为正整数.
通过二进制粒子群算法可以同时规划多个自治域的ECN最优部署,最终基于信息-电力混合熵的边缘计算节点部署规划方法流程如图1所示.
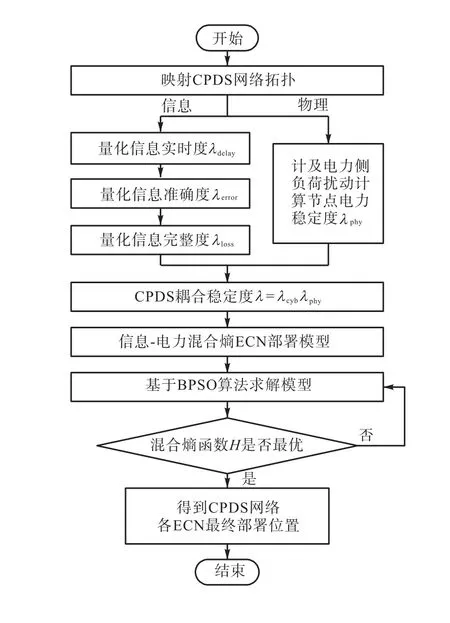
图1 边缘计算节点部署方法流程Fig.1 Flow chart of edge computing node deployment method
3 仿真实验及性能分析
本文选用IEEE39节点标准算例作为仿真实验的电力拓扑网络,其包括发电机节点10个、负荷节点21个、变压器节点12个和46条电力线路,表1为算例中发电机组参数.
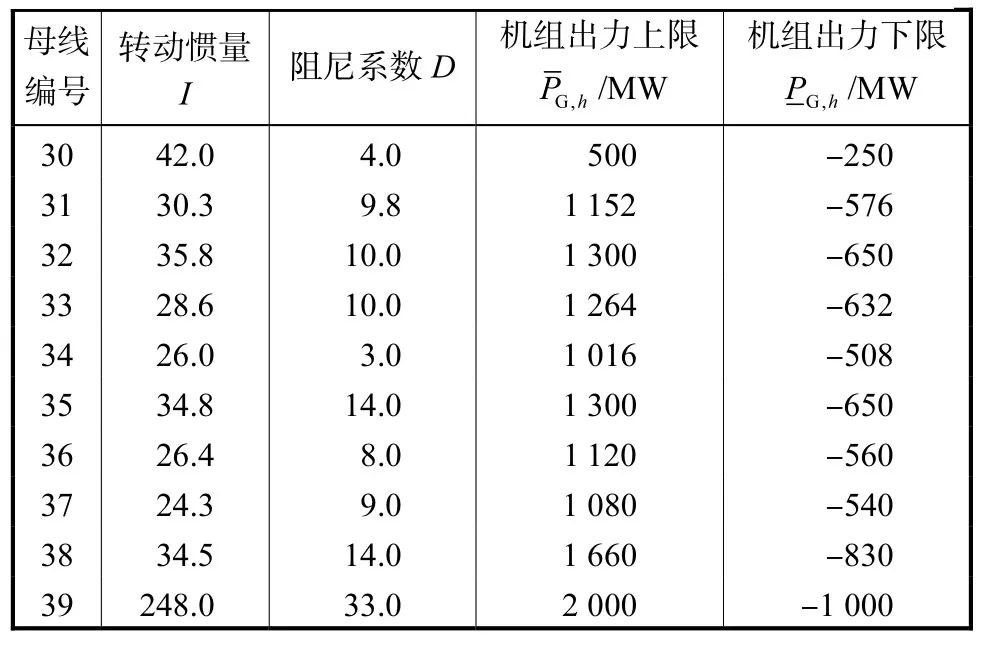
表1 标准算例发电机组参数Tab.1 Standard example generator set parameters
按照对全网节点全监控原则,电网中每个电气节点对应具备监控功能的通信终端设备,并且通信链路沿电力线走向组建紧耦合的通信信息网络.对于边缘计算本身特性而言,终端设备-边缘节点交互需要对状态量、测量量和参数传达进行快速可靠的计算处理和判断,基于此特性参照实际配电网通信场景,其通信参数阈值设置如表2所示[16-17].而对于链路利用率来说,通常遵循长相关、自相似的重尾分布,认为其服从威布尔分布.

表2 CPDS通信网络QoS阈值Tab.2 CPDS communication network QoS threshold
3.1 CPDS边缘节点部署分析
对于IEEE39节点算例网络,采用基于配网潮流进行区域划分求解,得到如图2所示的自治区域划分情况,其中每个自治区域内至少包含了一台出力机组,保证域内有功调度及无功支撑.进而采用信息-电力混合熵模型在基于自治域内计算最优ECN部署,结果如图2中星形和圆形标识位置所示.
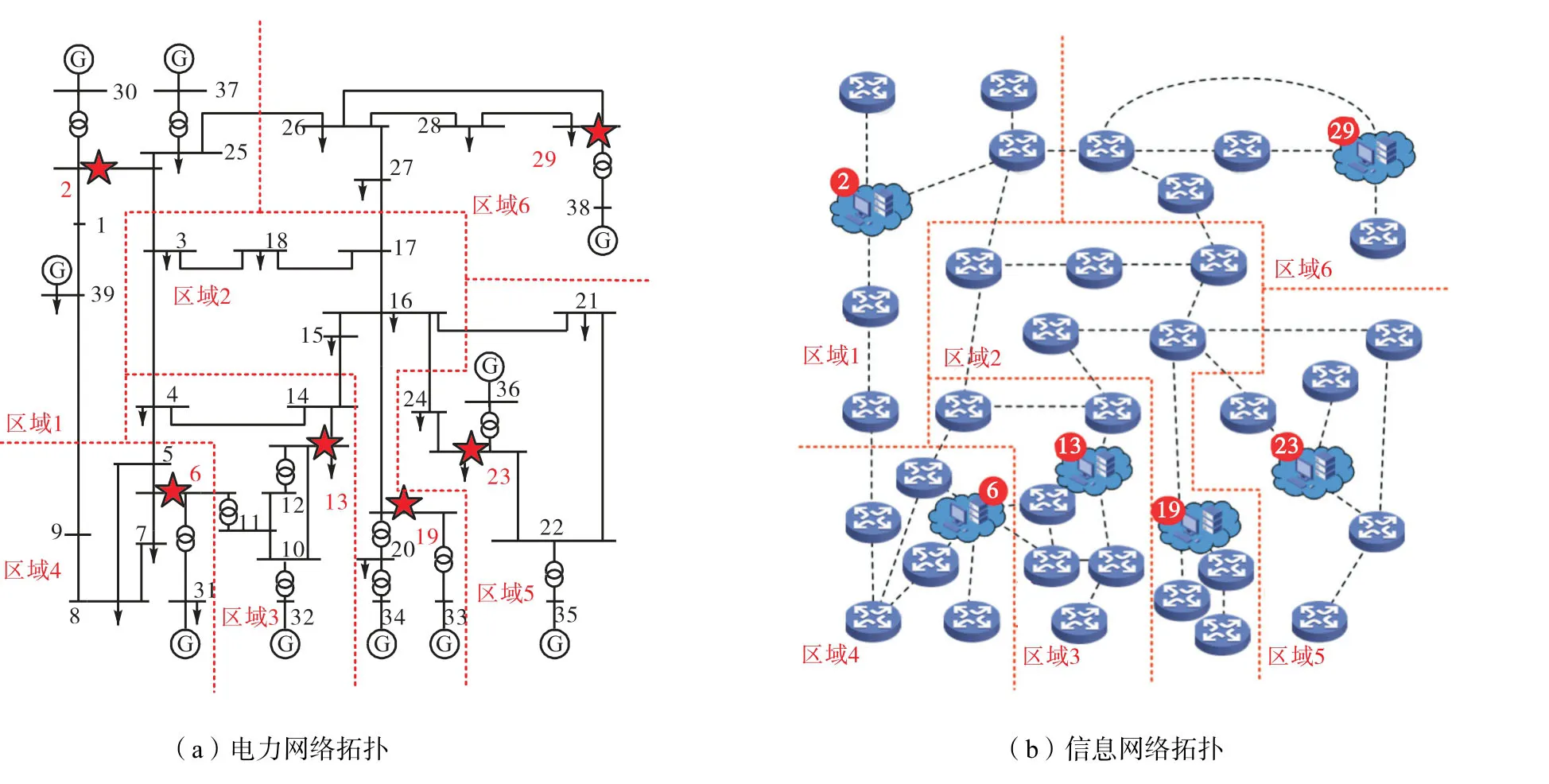
图2 IEEE39节点CPDS网络拓扑Fig.2 IEEE39 node CPDS topology diagram
CPDS网络最可靠时是整个网络熵值最大,即各终端设备与其区域内的边缘节点稳定度分布最为相近.为了更加直观地展现终端与边缘节点的拓扑情况和信息-电力稳定标度分布,将网络终端分布在k×k区域内.图3表示CPDS网络中边缘节点与其区域内的终端设备之间的信息-电力稳定度分布情况,此时网络熵值处于最大值为Hmax=3.5143.
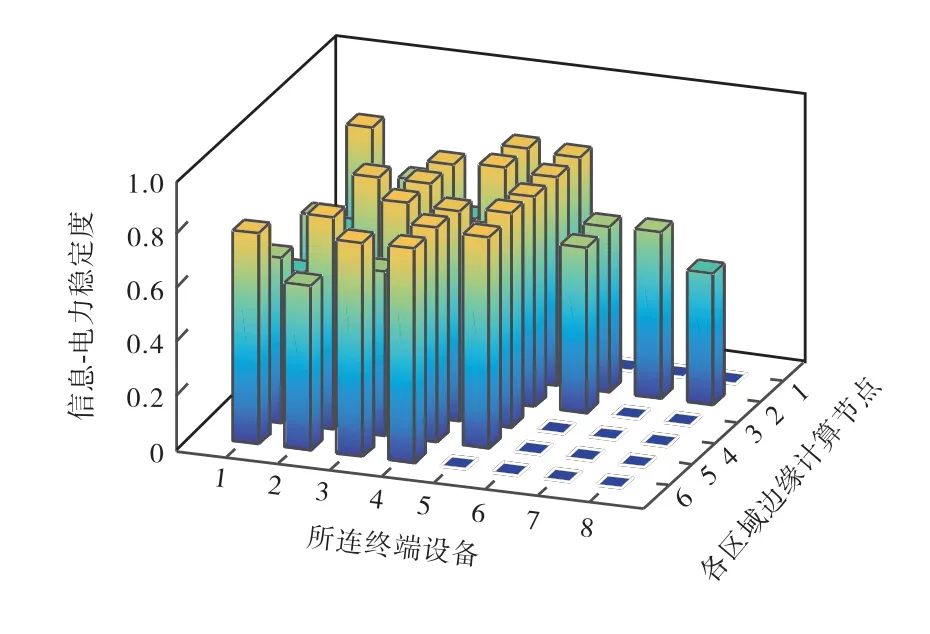
图3 信息-电力稳定度分布示意Fig.3 Schematic of cyber-power stability distribution
3.2 信息-电力稳定度分析
针对基于信息-电力混合熵的边缘计算节点部署结果,在此从CPDS网络节点电力稳定性与信息稳定性两方面进行对比分析.
3.2.1 节点电力稳定性分析
为验证所提方法对于仿真算例的边缘计算ECN部署的正确性,首先通过对网络中脆弱性节点辨识验 证本文所提节点电力特性判稳方法正确性.对比方法选用文献[18]经典灵敏度分析法,图4为各方法下节点电力脆弱性辨识结果.
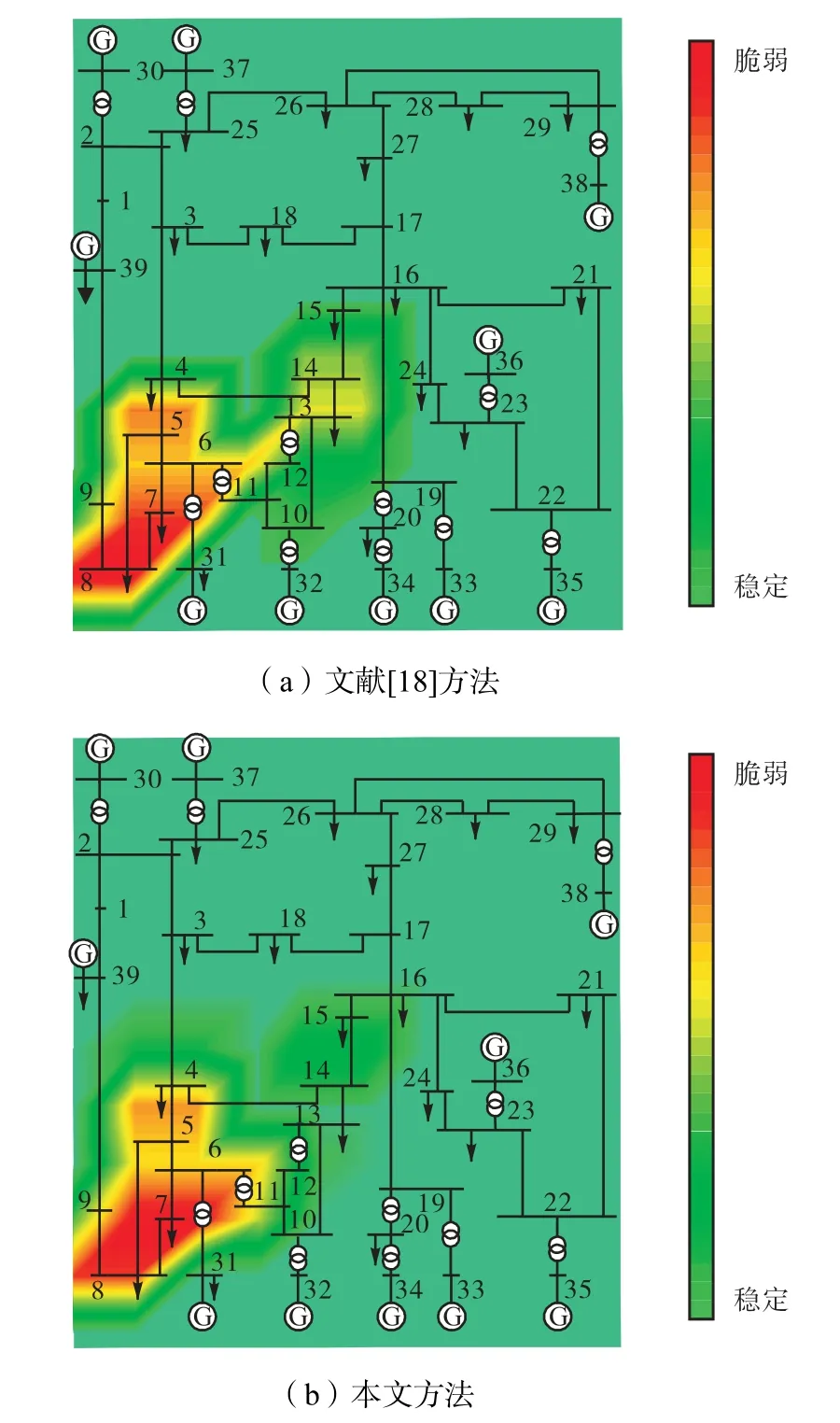
图4 节点电力脆弱性辨识结果Fig.4 Identification results of power vulnerability of nodes
由图4可知,本文采用节点电力稳定性分析方法对于网络中脆弱节点辨识结果与对比方法吻合,节点脆弱性区域集中在区域3与区域4中,其中节点7、节点8与节点5均为各方法网络中不稳定性较高的节点.由此可证实本方法可有效对CPDS中电力节点稳定性进行判定.
3.2.2 信息稳定性分析
本文进一步对CPDS网络信息稳定性进行分析.
设置CPDS网络流量如下:①以各类终端传感器周期采集上传数据为主的周期性数据流,流向为从传感器至ECN传输,每个采集报文长度为446 Bytes,发送间隔为0.02 s;②以终端设备控制类报文为主的随机性数据流,依照其短报文高实时性的流量特征设置单个数据长度为190 Bytes,发送间隔服从指数分布T~f(t)=100 e-100t;③此外,还考虑突发性数据流:主要映射CPDS系统异常期间产生的大量实时状态量报文和紧急控制类报文(如故障录波等)的突发性数据流,其具有突发数据量大、异常事件间相关性弱特点.仿真实验中采用OPNET通信网络仿真软件测试网络传输性能,图5给出边缘计算自治域4的通信信息子系统网络结构.其中,ECN优化部署于节点6位置.
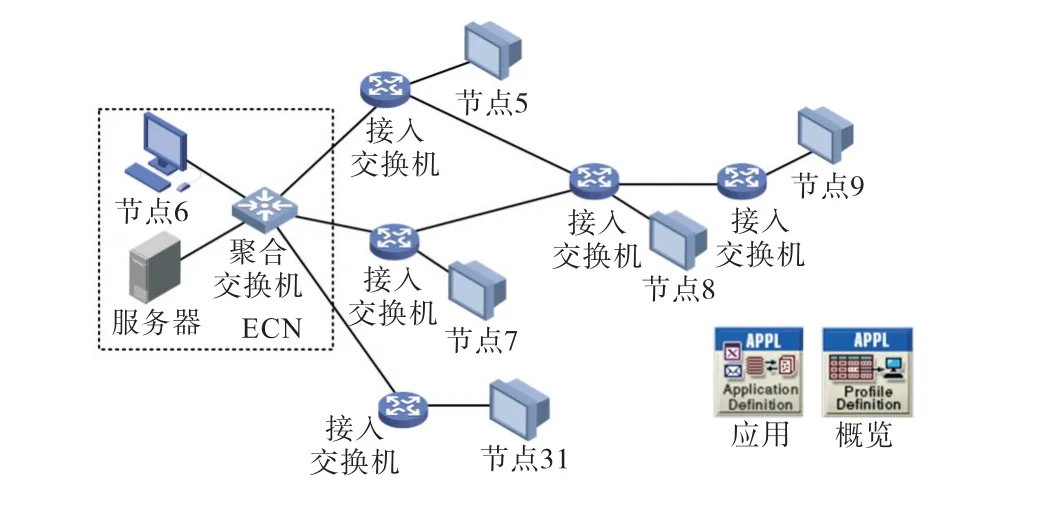
图5 区域4通信网络拓扑Fig.5 Area 4 communication network topology
实验模拟在系统运行t=4.1 s时节点7受负荷扰动并上传突发数据,ECN对其进行域内调度平抑控制.在此对比分析ECN设置在不同位置时CPDS网络通信性能.
图6给出了ECN在不同部署位置下的网络流量.由图6可知,不同部署方案对突发信息接收速度存在差异.当ECN部署节点6时,4.17~4.68 s接收节点7扰动信息,网络流量发生突增,经计算决策对其进行自治域内调度控制,表现为4.68 s后网络流量持续小抖动;与之相比,ECN部署至节点5处则在4.29~4.80 s收到节点7上报信息后实施本地控制;而部署于节点9时,ECN于4.47~5.01 s才收到突发信息.通过上述对比,可以看到在区域4中ECN放置在节点6处最优,对于异常状态信息收集速度明显优于其他部署方案.
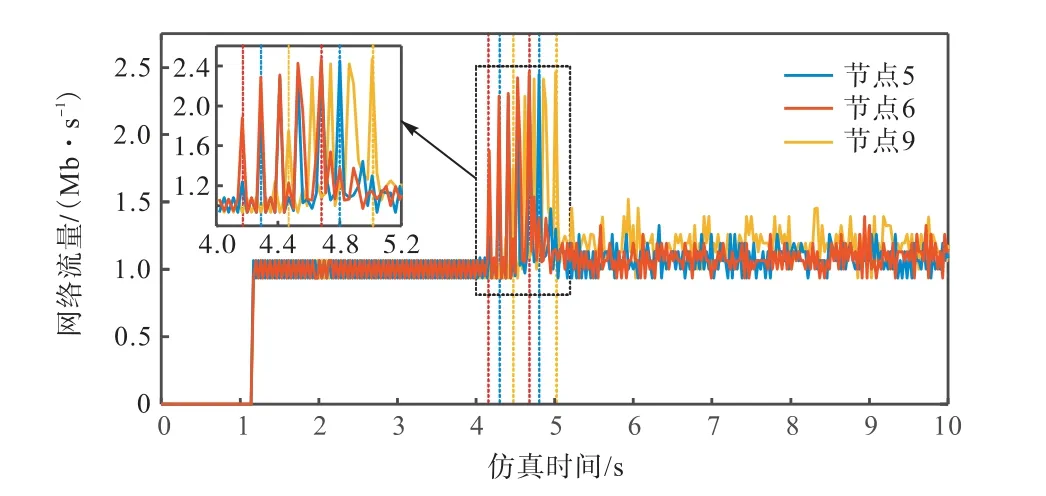
图6 区域4网络流量对比Fig.6 Comparison of network traffic in area 4
3.3 不同部署及计算模式下电网频率控制性能分析
为进一步分析ECN部署对于信息物理紧耦合的电力系统调度控制性能的影响,本文选择负荷频率控制(load frequency control,LFC)为例进行系统动态性仿真实验.
实验中设置母线7处产生0.1 p.u.的负荷波动,则自治域内母线31处发电机组对系统频率偏差进行平抑.参照IEEE39标准算例机组参数,采用经典PI控制,其模型参数设置如表3所示.

表3 负荷频率控制模型主要参数Tab.3 Main parameters of LFC model
实验比较了云计算集中式控制以及不同ECN部署情况下区域边缘控制模式下区域4内源-荷变化的频率调整过程,其中网络时延参数如表4所示.

表4 单区域网络时延参数Tab.4 Network delay parameters of single area network
图7给出不同控制模式下系统频率偏差及阻尼动态过程.由图7可知,网络控制性能因在不同的计算模式及ECN部署情况下存在明显差异性.基于云计算集中式控制时,由于网络时延影响,致使系统频率控制存在滞后性,机组出力无法有效实时跟踪负荷波动,LFC超调相对其他模式下较大,在3.03 s时频率偏差达到最值-0.021 Hz,且系统阻尼过程缓慢,在25.0 s后还未收敛稳定;而与之相比,边缘计算模式近设备侧控制,使得系统频率可较为快速达到收敛值,保证系统频率稳定.其中将ECN设置在节点6处 情况下,同云计算集中式控制相比可将系统频率最大偏差降低16.43%;并且频率偏差可在15.81 s实现有效收敛,比设置在节点5时的22.35 s收敛具有更好的动态性能.
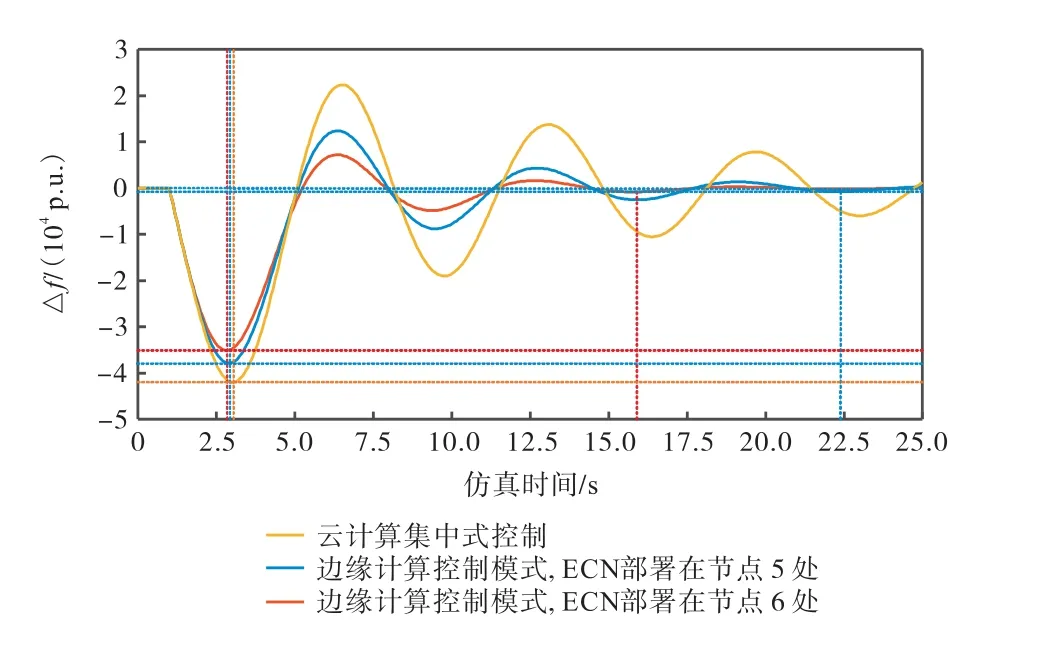
图7 不同控制模式下系统频率偏差及阻尼过程Fig.7 System frequency deviation and self-tuning process under different control modes
4 结 语
针对CPDS分布式边缘计算新需求和节点部署可靠性问题,本文研究并提出一种配电信息物理系统边缘计算节点优化部署新方法.建立了CPDS信息传输稳定度计算模型、电力稳定度计算模型和CPDS信息-电力混合熵计算模型,基于熵最大原理实现对CPDS网络边缘计算节点的最优化部署.研究有效提升对网络状态获取时效性,实现对CPDS本地负荷频率控制的快速响应.后续还将针对ECN资源分配和工程部署时即插即用实现开展研究.

