具有奇异势的拟线性分数阶扩散方程解的爆破性

李建军,王看看,徒君

(辽宁工程技术大学理学院,辽宁 阜新 123000)

1.引言

分数阶Laplace算子是一类非局部椭圆算子,它在物理现象,反常物理现象中运用广泛,而且分数阶Laplace算子比经典Laplace算子能更好地描述实际问题,因此引起了数学和物理学家的广泛关注[1].分数阶拟线性偏微分方程是一类特殊的反应扩散方程,随着科学的迅速发展,为了适应各个学科领域研究的需要,反应扩散方程这类非线性偏微分方程得到了深入的研究和广泛的发展[2].例如樊佳幸[3]借助Sobolev嵌入定理,Gagliardo-Nirenberg不等式,利用Galerkin方法研究了一类带有扩散项的非线性抛物方程组的初边值问题弱解整体存在和爆破的充分条件.杨慧,王建[4]利用上下解方法研究了一类具有非局部非线性Neumann边界条件和非线性吸收项的非局部反应扩散方程解的存在性和爆破性.薛应珍,冯贺平[5]利用上下解方法研究了一类具有加权非局部边界和非线性内部源的多孔介质抛物型方程组解的渐近性态.

在数学理论上,反应扩散方程的全局解和爆破解可以理解为: 在局部解存在的条件下,如果局部解能延拓到整个时间t →∞,此时称该局部解为整体解;如果局部解只能延拓到某个有限的时间T,即当t →T时,局部解趋向无穷,此时称该局部解在有限时间T内爆破,且T称为该解的爆破时刻.关于分数阶反应扩散方程解的爆破性研究甚少,如LIN,TIAN等人[6]通过引入一种新的辅助函数和自适应凹法,研究了含有分数阶Laplace算子的Kirchhoff型波动方程初边值问题解的爆破和爆破时刻.

在分数阶条件下,FU和Pucci[7]研究下列空间分数阶扩散方程解的全局存在性和爆破性:

由于分数阶Laplace算子的非局部性,利用Caffarelli-Silvestre扩展方法[9]将非局部性问题(1.1)转化为更高一维的局部椭圆型方程定解问题.更精确地,v=Es(u):Ω×(0,∞)→R作为问题(1.1) 中u:Ω →R的扩展函数,记C={(x,y)|(x,y)∈Ω×(0,∞)}及它的侧边界为∂LC=∂Ω ×[0,∞).根据文[10]知,(-Δ)s是函数v在Ω ×{0}上的Dirichlet-Neumann算子,即

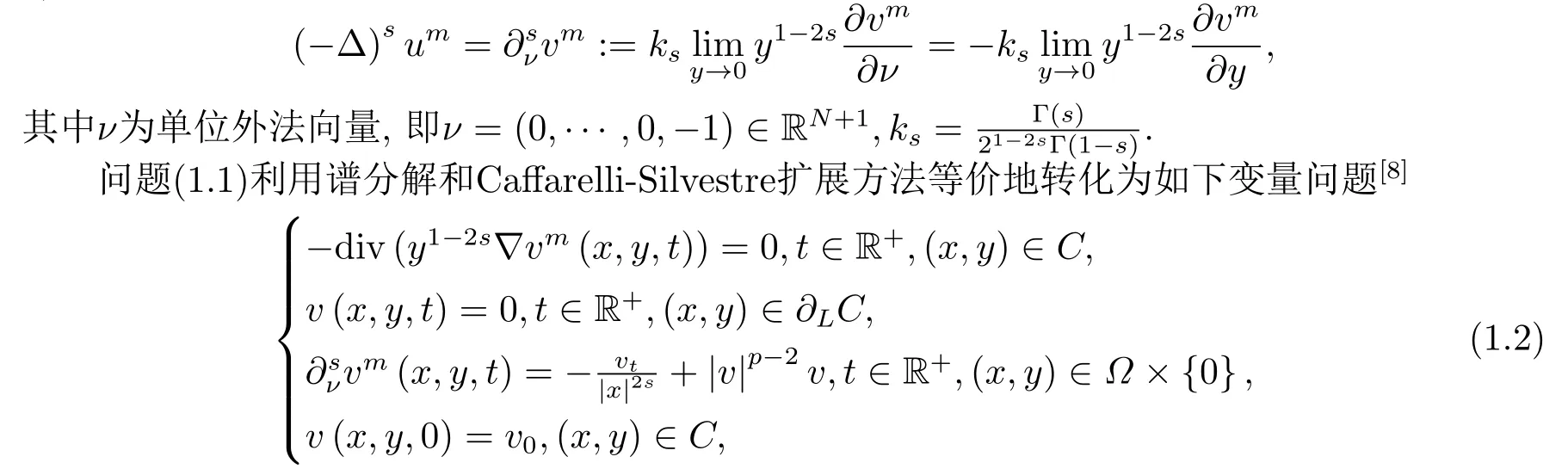
这是一个具有动力边界条件的局部椭圆型方程定解问题.类似于文[8]中m=1的情况,(1.2)的能量泛函定义为

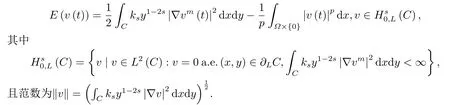
本文的主要结果是

定理1如果v=v(x,y,t;v0)是(1.2)的全局解,v0∈Σ1,那么存在α ＞0,使得

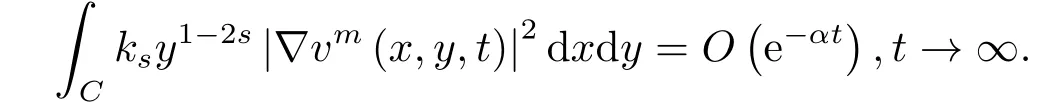
定理2如果v=v(x,y,t;v0)是(1.2)的全局解,且在函数空间(C)中关于t一致有界,那么对于每个序列tn →∞,存在一个平稳解w,使得在(C)中有v=v(x,y,tn;v0)弱收敛于w.

定理3如果v=v(x,y,t;v0)是(1.2)的解,且存在t0≥0使得E(v(t0))≤0,那么解v在有限时间内爆破.

定理4如果v=v(x,y,t;v0)是(1.2)的解,v0∈Σ2,那么解v在有限时间内爆破.

2.准备知识

3.解的衰减估计,长时间渐近性态及爆破性

根据文[8],由类似方法得到本文所考虑的具有奇异势的拟线性分数阶反应扩散方程解的全局存在性,在全局解存在的基础上,讨论全局解的衰减估计、长时间渐近性态以及局部解的爆破性.基于Nehan 流形,位势阱,不稳定集合,位势阱的深度,本节通过能量法给出全局解的衰减估计,长时间渐近性态;利用凹函数法,得到局部解在有限时间内爆破的充分条件.

定理1的证明根据位势阱Σ1的等价定义,对所有的t ≥0,H(v(t))＞0,因此

定理证明方法与文[8]类似,故剩下的证明过程参考文[8].

定理3的证明关于解的爆破性证明方法有比较法,特征函数法,能量法,及本文采用的凹函数法[13,15].

论证的其余部分与定理3的证明方法类似,因此剩下的证明参考定理3.