大地电磁与接收函数结构约束联合反演

甘露, 吴庆举, 黄清华, 张慧茜， 唐荣江

1 中国地震局地球物理研究所， 北京 100081 2 北京大学地球与空间科学学院， 北京 100871

0 引言

随着地球物理技术的发展，对地下目标详细的、多属性参数探测的需求日益增加，这在很大程度上促进了自动化综合地球物理新方法的发展，特别是联合反演方法的更新(Julià et al., 2000; Gallardo and Meju, 2003; Moorkamp et al., 2007; Moorkamp, 2007; Haber and Holtzman Gazit, 2013).本文尝试了对不同地球物理参数敏感的大地电磁和接收函数数据的联合反演.大地电磁数据对地下地质体的电性结构敏感，而接收函数对速度的突变界面敏感.虽然在地壳和地幔中，这两种参数的变化并不是严格空间相关的，通常来说，对于大地电磁，电性结构的异常通常存在于岩体的次要成分，比如石墨、硫化物，或者渗入岩石内部的流体，这些通常对地震方法来说探测比较困难；但是，同样也存在许多物理参数将会同时影响电导率和速度，例如温度和孔隙度等.此外，在一些主要的岩性边界，电导率和速度这两种参数都会发生改变 (Marquis et al., 1995; Lahti et al., 2005; Tournerie and Chouteau, 2005)，即使影响电导率的是石墨，也可以认为是构造活动决定了石墨体的存在和规模，该构造活动也同样决定了地震波速度(Carcione et al., 2007).此外，两个主要的边界即莫霍面和岩石圈边界也明显与电导率的变化相关(Jones, 1999; Jones and Ferguson, 2001; Gatzemeier and Moorkamp, 2005).因此，可以预料到，接收函数与大地电磁联合反演得到的两种模型，存在一定的结构相似性.

大地电磁和接收函数联合反演的目标是重建地壳乃至上地幔结构，一个主要的挑战是：在实际情况中，高速(低速)异常和高阻(低阻)异常不一定完全对应 (Jones et al., 2009).在地壳内部，对于速度结构来说，随着深度的增加，由于岩石压力增加，导致岩石更加致密，密度和波速也增大.即使在地幔热物质存在的区域，波速会下降但不会影响速度的整体变化趋势.电阻率的大小主要受温度、压力以及含水量的综合影响，电阻率与压力成正相关，与温度和含水量成负相关.随着深度的增加，温度和压力都会增加，含水量也会发生变化，电阻率受到三者综合影响总体上呈下降趋势，局部出现反弹.地震波速度和电阻率在深部的变化规律使得它们很难通过经验公式联系起来，通常情况下经验公式来源于测井数据，而测井数据通常较浅，一般不超过8 km；另一方面，如果使用共享部分属性(例如层厚等)信息实现联合(Moorkamp, 2007)，需要设定较少的层数实现约束，其实质是将约束条件下的欠定问题变为适定或者超定问题，然后寻找共同界面下的最优解.目前主流的大地电磁与接收函数联合反演是通过共享界面来达到联合反演的目的，而未加入模型耦合项，假设不同观测数据对相同的异常都具有敏感性 (Moorkamp et al., 2007, 2010; Moorkamp, 2007; Zevallos et al., 2009; 彭淼等, 2012).然而这种方法限制了模型反演的灵活性.在该方法中，使用多目标函数遗传算法NSGA-2(Deb et al., 2002)寻找的帕累托最优解是基于少量的模型层数，难以找到约束条件下两个目标函数的全局最优解.当层数较多时，两个模型是解耦的，分别都能找到各自的最优解.因此，联合反演的一个最大挑战在于找到既可以提供模型足够的自由度去拟合所有观测特征，又可以耦合两种不同属性的模型(Moorkamp, 2007).为了在维持模型一定自由度情况下，提高模型的耦合程度，本文提出新的约束算子用于速度和电阻率模型相似度约束.

接收函数与大地电磁的反演不但针对不同的物性，它们各自本身属性也具有较大差异.接收函数属于地震信号序列，控制方程为波动方程，信号的强弱受波阻抗界面的控制；电磁场的控制方程在低频段的地下介质中满足传导方程，信号强弱受区域内地球内部电阻率的综合影响.这些差异使得两种反演方法具有完全不同的特性.接收函数对于地层分界面敏感，对绝对速度的约束较弱，这导致它虽然具有较高的分辨率，但是严重受到初始模型的影响(如，Ammon et al., 1990; Kind et al., 1995; Tomlinson et al., 2006)；大地电磁对于电性界面没有很好的分辨能力，但是对于绝对电阻率属性约束较好，且受初始模型的影响相对接收函数较弱.综上可以推测，大地电磁和接收函数的联合反演具有一定的互补性.本文将通过理论模型和实际资料的测试，探索联合反演能否降低二者单独反演中的非唯一性.

本文采用拟牛顿法对目标函数进行优化，寻找最优解.拟牛顿法是梯度类反演中最具代表性的，也是大型非线性问题中最优秀的方法之一.拟牛顿法的本质是牛顿法的近似，它通过近似迭代求解牛顿法中计算量最大的Hessian矩阵，保证了模型的二阶(曲率)下降.与线性化的方法和全局搜索类算法相比，梯度类的算法通常基于Tikhonov 正则化方法，可以很方便地建立不同目标函数以及约束项求和形式.为了设定足够的反演参数，同时促进两个模型找到最优耦合形式，一个合理的方法是建立起电阻率模型和速度模型的联合算子项，作为目标函数需要优化的多项式之一，这种方案是目前结构相似算法普遍采用的方案，例如Gallardo和Meju(2003)提出的交叉梯度联合反演.受到交叉梯度方法的启发，本文将设计速度模型和电阻率模型的一维梯度耦合算子，使用拟牛顿法同时优化大地电磁、接收函数以及联合算子项，实现大地电磁与接收函数的联合反演.

1 联合反演方法

接收函数和大地电磁的联合反演通过最优化共同的目标函数来实现：

φ(mse,mem)=φse(mse)+φem(mem)+φjoint(mse,mem),

(1)

其中，φse为接收函数的目标函数，φem为大地电磁的目标函数，φjoint为电阻率和地震模型的联合算子，具体展开形式如下：

(2)

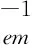
(3)

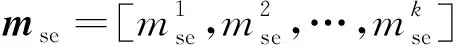
此外，Vse和Vem分别对应两种数据的协方差矩阵的对角线元素(Egbert and Kelbert, 2012)，以Vse为例，Vem的形式与Vse一致，其表达式为：

Vse=diag{E[(X-E[X])(X-E[X])T]}

(5)

这里X为由观测数据组成的向量.在实测数据中，由于每个元素都有大量的采样，因此可以对每个元素求取方差.该矩阵可以让方差较大的观测数据在参与目标函数的计算中占有较小的比重，以保证当观测数据质量较差时反演能够稳定进行.在合成数据的测试中，由于数据是没有误差的，Vse和Vem取单位矩阵.

在反演中，速度模型和电阻率模型共享层厚和权重，假设反演层数为k，目标函数的梯度可以写作：

(6)

由于假设模型为一维层状介质，这对于接收函数和大地电磁的反演来说计算量较小，因此，本文总是同时反演三项目标函数，速度模型和电阻率模型在反演中同步更新.

另一个值得注意的问题是，在联合反演中，目标函数中的每一项应保持在同一个数量级上，以防止目标函数仅以拟合较大项为目的而忽略了较小项的拟合.接收函数的值一般位于[-0.3,0.8]之间；对于大地电磁，假设视电阻率的取值范围为[1,100000]Ωm，那么对其取对数后的取值范围为[0,5].这个范围大于接收函数的观测值，因此这里用二者观测数据的最大值对各自的观测数据进行归一化，同时消除采样点数的影响.此外，协方差矩阵也可能造成目标函数项之间的量级差，特别是值较小的方差可能造成目标函数的值突然增大，为了减小方差影响，对原数据加权矩阵作以下处理:

V′=γ2N(V+E),

(7)

其中γ为观测数据的最大值；E为单位矩阵，N为各自的采样点数.γ2N消除了接收函数和视电阻率数据量级的差异，以及采样点数的差异，E消除了小方差的影响.

从公式(4)可以看出，φjoint通过极小化电阻率模型和速度模型的纵向梯度绝对值之间的差异来实现二者在空间上的耦合.其中，方括号里的平方是为了同化梯度的方向，即不论模型逐渐增大还是逐渐减小，只要梯度的绝对值一致，都认为它们具有相似性.这更加符合地壳尺度的反演，因为在地壳内部速度随着深度的增加总体上逐渐上升，而电阻率总体呈下降趋势.方括号外的平方是为了保持目标函数为凸函数，使其在反演中总能寻找到极小值.在反演中可以设计足够层数的模型，使得算法找到拟合观测数据的模型参数；同时联合算子保证了两种模型的相似性，即既能够维持足够的模型自由度，又同时耦合了两种模型.

本文采用拟牛顿法来极小化目标函数，拟牛顿法的基本思想是根据在每次迭代中储存前m次的模型以及梯度修正量，以尽可能小的计算代价构建近似Hessian矩阵，进而求得近似的牛顿下降方向，保证模型的二阶下降属性(Byrd et al.,1994,1995).除了计算下降方向以外，还需要一个合适的步长以保证模型的充分下降.通常基于Wolf准则，采用二次插值算法，回溯迭代来搜索一个合适的步长.本文对有限内存拟牛顿法(L-BFGS)开源代码(Byrd et al., 1994, 1995; Zhu et al., 1997; https:∥github.com/stephenbeckr/L.BFGS.B.C)进行修改后完成接收函数与大地电磁联合反演.梯度类反演方法总是从一个初始模型开始，不断迭代更新以逐渐逼近真实解.接收函数由于对绝对速度不敏感，导致反演结果高度依赖初始模型(Ammon et al., 1990; Kind et al., 1995; Tomlinson et al., 2006)，且大地电磁反演结果也一定程度上受到初始模型的影响，因此选择合适的初始模型对反演具有重要意义.对于电阻率模型，通常采用均匀半空间为初始模型，以适用于地壳尺度的大地电磁反演(Zhang et al., 2016；叶涛等，2021)；对于速度模型，初始模型修改自全球速度模型ak135(Kennett et al., 1995).

2 理论模型测试

为了验证算法的有效性，本节设计了耦合的理论速度模型和电阻率模型进行测试，电阻率模型和速度模型总是在异常处耦合，但是异常的正负不完全对应，这更加符合真实地壳结构.每个模型的反演层数设定为80层，反演深度70 km.接收函数正演时窗为-5～46.2 s，采样间隔0.1 s，共512个采样点数，以方便进行快速傅里叶变换.反演中仅需要反演部分时窗，即-5～25 s，采样点数为300.接收函数的射线参数设定为0.055，高斯滤波系数设定为2.5.大地电磁数据的频率范围为 0.001～100 Hz，以对数间隔共设定40个采样点.权重参数α1=1.0，α2=1.0，正则化因子λ1=λ2=0.1.目标函数的终止受控于梯度的最大分量和目标函数的变化率，根据Byrd等(1995)，当满足以下条件之一时，目标函数终止：

(8)

这里fk为第k次迭代的目标函数，g[i]为梯度的第i个分量，l为模型的层数；pgtol为人为设定参数，在本文中设定为10-5；epsmch为机器精度(machine precision), 64位机通常为2-53，factr设定为1010.可以看出，第一个条件的物理意义为梯度足够小，第二个为目标函数无法下降或者反弹.

图1设计了一组耦合的低速-低阻模型，可以看出电阻率模型和速度模型在形态上具有较大差异，然而在某些界面处，特别是低速-低阻处模型结构是耦合的，这在地壳结构中是非常常见的.由于25 km处低阻层较薄，单独的大地电磁反演无法有效约束出低阻层的具体位置，而联合反演中25 km处低阻异常明显，大地电磁在深部的分辨率明显提高.从空间梯度分布图可以看出，电阻率模型梯度的平方随深度变化，其极值对应着梯度变化的极大值，也就是模型剧烈变化的区域.与单独反演相比，联合反演后速度模型和电阻率模型的空间梯度更加吻合，这说明在反演中联合反演算子使得两种不同属性的模型朝着相似的方向变化.

图1 模型I含低阻层时接收函数与大地电磁联合反演结果(a) 单独反演； (b) 联合反演，联合反演参数β=3.0,=1.5 .中间子图为每个部分的数据拟合结果， 上图为接收函数的数据拟合，下图为大地电磁视电阻率的数据拟合；右图为两个模型的归一化后的空间梯度平方分布.Fig.1 Joint inversion of receiver function and magnetotelluric for model I with low resistivity layer(a) Separate inversion; (b) Joint inversion with β=3.0,=1.5. The middle sub-figure is the data fitting result of each part, the upperFigure is the data fitting of the receiver function, the lowerFigure is the data fitting of the magnetotelluric apparent resistivity; the rightFigure is the distribution of normalized spatial gradient square from the two models.

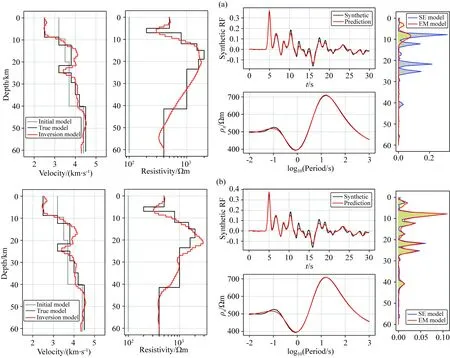
图2 模型I不含低阻层的接收函数与大地电磁联合反演结果(a) 单独反演； (b) 联合反演，联合反演参数β=3.0,=1.0.各子图的解释与图1相同.Fig.2 Joint inversion of receiver function and magnetotelluric for model I without low resistivity layer(a) Separate inversion; (b) Joint inversion with β=3.0,=1.0. The description of each subgraph is the same as that in Fig.1.

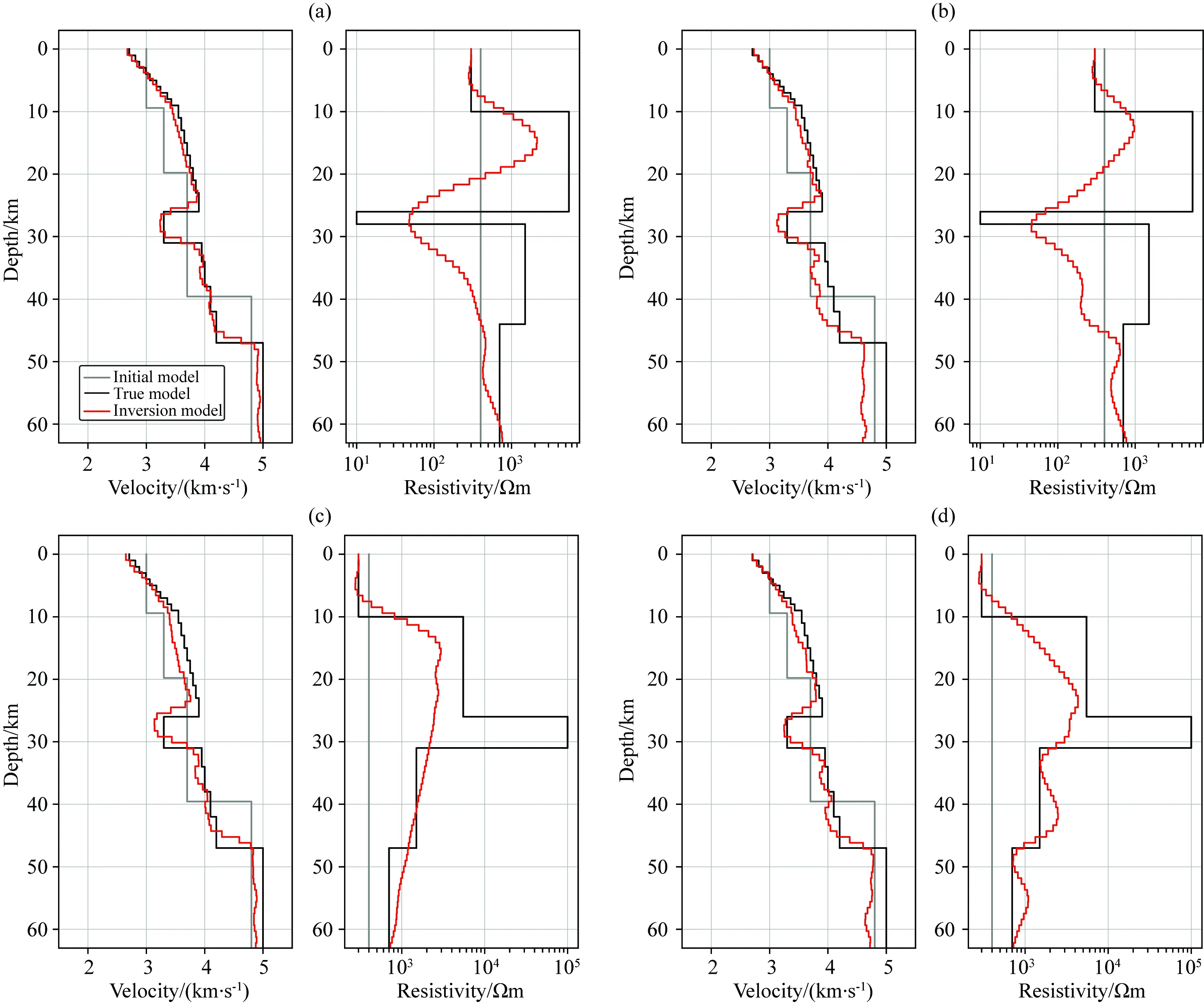
图3 模型II接收函数与大地电磁联合反演结果 (a)(b) 含低阻异常的单独反演与联合反演结果； (c)(d) 含高阻异常的单独反演与联合反演结果，联合反演参数β=1.0,=1.5.Fig.3 Joint inversion of receiver function and magnetotelluric for model II (a)(b) Separate and joint inversion results with low resistivity anomalies; (c)(d) Separate and joint inversion results with high resistivity anomalies,β=1.0,=1.5.

图4 模型III接收函数与大地电磁联合反演结果(a) 单独反演； (b) 联合反演，联合反演参数β=1.0,=1.5.各子图的解释与图1相同.Fig.4 Joint inversion of the receiver function and magnetotelluric for model III(a) Separate inversion; (b) Joint inversion with β=1.0,=1.5. The description of each subgraph is the same as that in Fig.1.

图5 (a) 工区台站分布图，红色圆圈为大地电磁台站，蓝色三角为地震台站. (b)联合反演目标函数随β演化曲线， 红色虚线表示被选中的β值，φjoint下降98%Fig.5 (a) Distribution of stations in the work area. The red circle shows magnetotelluric stations, and the blue triangle shows the seismic stations. (b) β evolution curve for joint inversion objective function terms. Red dotted line indicates the selected β, which corresponds to φjoint decreased by 98%

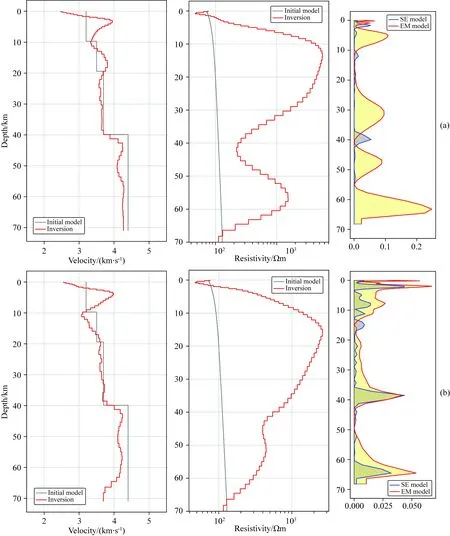
图6 地震台站A504和大地电磁台站1141n5TM模式联合反演结果，右图为归一化后的空间梯度平方的分布图(a) 单独反演； (b) 联合反演，联合反演参数β=2.5,=1.0.Fig.6 Joint inversion of seismic station A504 and magnetotelluric data of station 1141n5 for TM mode. The rightFigure shows the distribution of normalized spatial gradient square(a) Separate inversion; (b) Joint inversion with β=2.5, =1.0.

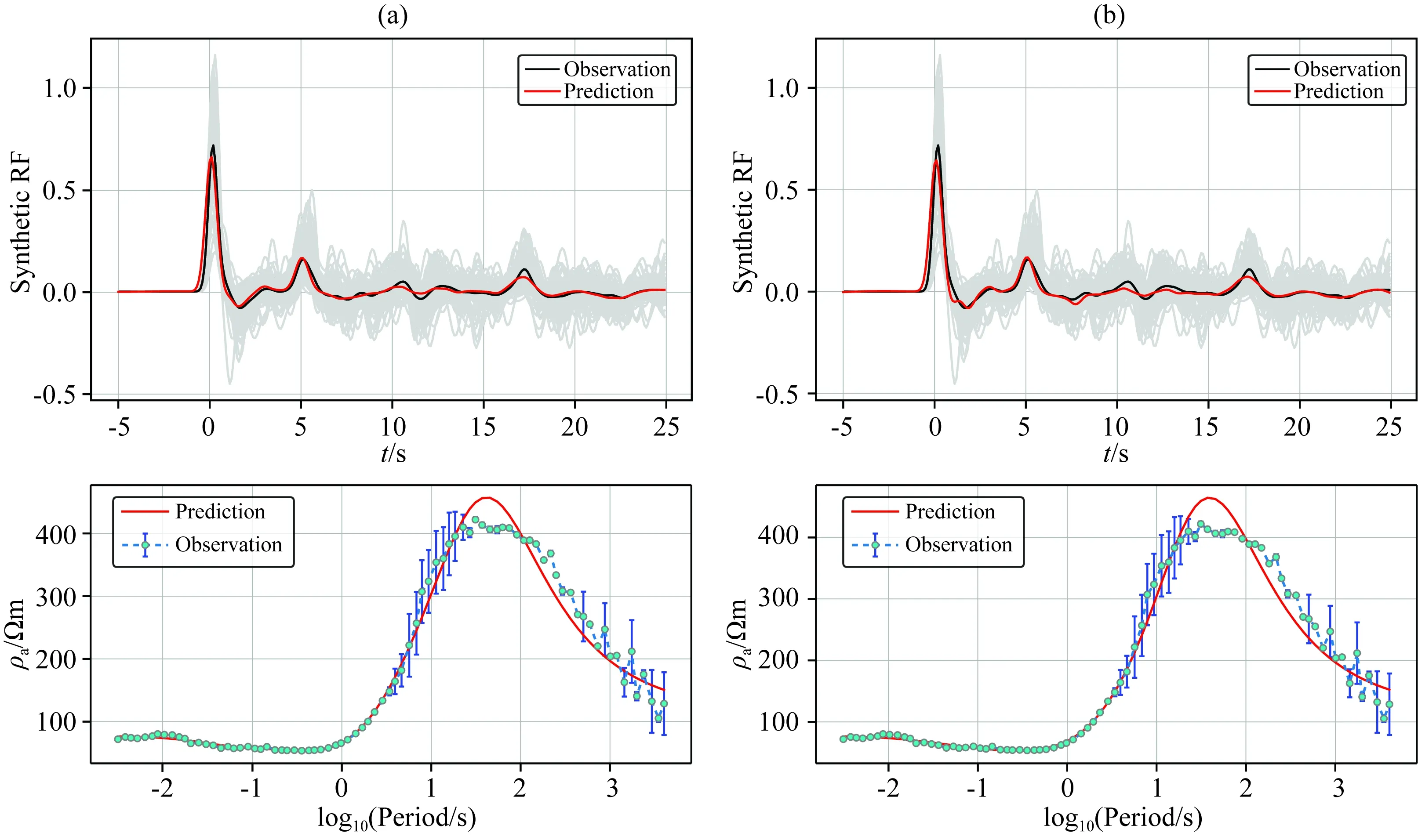
图7 地震台站A504 和大地电磁台站1141n5数据拟合结果 在第一排中，灰线为叠加之前的接收函数.(a) 单独反演； (b) 联合反演.Fig.7 Data fitting of seismic station A504 and magnetotelluric station 1141n5 In the first row, the gray line is the receiver function before superposition.(a) Separate inversion; (b) Joint inversion.

为了进一步测试模型不耦合的情况，在图2中，对图1中的模型进行修改，保留速度模型的低速异常，去掉了电阻率模型的低阻异常.可以看出，联合反演的结果与真实模型对应良好，没有出现假异常，但是由于速度模型的约束，在对应的地方出现了一定的跳跃变化，这也对应着模型附近的空间梯度异常.这说明联合反演对于速度模型和电阻率模型不耦合的情况有一定的辨识能力.

此外，在实际情况中，电阻率和速度不一定成正相关.为了验证联合反演算法是否适用于不同情况，分别设计了高阻和低阻异常进行测试(图3)，两种电阻率模型都对应着低速异常.可以看出，当低阻异常存在时，单独反演可以约束出异常的位置，而联合反演使得异常进一步突出，且在45 km的界面处出现明显跳变，联合总体上优于单独反演.然而，从图3c,d可以看出，联合反演对于高阻异常的约束能力不如低阻异常，联合反演没有出现明显的高阻异常，仅在异常处呈现一个跳变，这种跳变是速度模型约束的结果.尽管如此，联合反演结果总体上优于单独反演，在单独反演中的电阻率模型平缓，没有任何异常；而联合反演能更好的识别出主要电性界面的位置.同样，在图4中，联合反演相比单独反演能更好的约束出电性界面的位置，这种界面往往是速度和电阻率模型共同的界面，可以从空间梯度平方的分布图上明显识别出来.在图1b,2b,4b中，联合反演视电阻率的拟合效果均比单独反演稍差，这是因为在联合反演中不仅需要极小化观测数据与正演数据之差，同时需要极小化联合算子，因此，联合反演的数据拟合程度一般会略低于单独反演.

从以上讨论可以看出，在联合反演中，速度模型对电阻率模型有较好的约束能力，而速度模型受电阻率模型影响较小，其主要原因在于大地电磁数据对深部结构的约束能力较弱，电磁场的观测资料相对于接收函数对深部局部异常变化的敏感性较低.本文联合反演实质是通过空间梯度上的一致性，达到两种模型相互约束的目的.大地电磁反演中的多解性主要体现在局部的模型变化，例如薄层、互层、异常体等可以对应着相同的观测数据，而接收函数的多解性主要体现在由于绝对速度的偏差导致模型整体的平移，例如对于简单两层地壳模型，一个相对低速莫霍面较浅的模型和另一个相对高速、但是莫霍面较深的模型对应着同一个观测数据(Ammon et al., 1990).两种方法多解性问题的体现是不一样的，而联合算子使用梯度并不能对整体速度结构进行约束，这解释了为什么电阻率模型对速度模型的约束不明显.

3 实际数据应用

本节对实测数据进行接收函数与大地电磁联合反演，以进一步测试算法的适用性.在华北地区选择了一组相邻大地电磁和地震台站，其具体位置如图5所示，两种数据都具有较高的信噪比.

接收函数数据来源于中国地震局地球物理研究所布设于华北的A504台站.首先筛选出来自该台站的震级在5.5级以上，震中距在30°到95°之间的事件，并对数据进行预处理，主要包括事件提取、去倾斜、去趋势、去均值、滤波、降采样等；然后采用迭代时间反褶积(Ligorría and Ammon, 1999)计算接收函数，高斯滤波系数采用的是2.5，然后截取P波初至的前5 s和后25 s作为接收函数的有效时窗，得到采样频率为10 Hz、共300个采样点数的接收函数.

对于大地电磁实测数据，首先对电磁场各个分量的时间序列进行傅里叶变换(Thomson, 1982)，得到频率域的电磁场数据，然后使用平均交叉谱(Sims et al., 1971)估计得到阻抗张量，并使用远参考点法(Gamble et al., 1979)以进一步减少由非平面波场或仪器噪声等原因造成的计算偏差.

联合算子权重β的取值对反演结果有重要影响，随着β的不断增大，目标函数可能陷入局部极小，数据拟合不充分，然而过小的β值将导致联合算子不能很好的约束两个模型朝着相似的方向演化.因此，本文的调整β值的准则为：一方面需要保证模型可以很好的解释观测数据；另一方面，希望联合算子在反演中约束两种不同属性的模型朝相似方向演化.因此，这里计算了不同β情况下，不同目标函数项的RMS曲线，尽可能选择一个合理的β值使得联合算子项既占有足够的比重来对模型进行约束，又确保大地电磁和地震数据充分下降(图5b).最终选择β=2.5，此时φjoint从1.08下降到0.027，下降程度98%.

图6为接收函数和大地电磁联合反演结果，可以看出，与单独反演相比，联合反演的电阻率模型在莫霍面附近出现明显的跳变，与地震模型匹配良好.在单独反演中，两者梯度变化的极值完全不相关，说明模型完全解耦；而在联合反演中，两种模型的梯度匹配良好，在地表，40 km莫霍面，以及65 km处梯度同时出现极大值，表明速度模型和电阻率模型在该地区发生明显变化，而其余地区两者梯度变化平缓.由于速度模型在地表以及莫霍面的约束，电阻率模型在这两处相对于单独反演出现更加剧烈的变化；而在深部65 km处，电阻率模型变化率较大，引起这种变化主要的原因是观测数据对最后一层电阻率相比倒数几层更为敏感.电阻率的梯度对速度模型形成约束，联合反演后速度模型出现低速异常，然而大地电磁的异常在该深度上存在不确定性，因此不能判断速度的异常为真实异常.此外，由图7可以看出，单独反演和联合反演都能较好的拟合观测数据，且联合反演中φjoint出现明显下降，这说明联合反演找到了耦合的电阻率模型和速度模型.

实际数据的拟牛顿联合反演测试表明，该联合反演算法一定程度上提升了大地电磁深部的分辨率，特别是在莫霍面附近电阻率模型被约束出明显的异常，这对于大地电磁的解释来说至关重要.在深部，大地电磁对于速度模型的约束相对微弱，主要原因在于大地电磁对于深部的局部异常例如薄层或突变界面等敏感度较弱，模型的局部变化对于视电阻率的影响是微弱的，这使得目标函数更容易约束电阻率模型以实现联合算子下降.

4 结论

合成数据和实际观测资料证实了拟牛顿算法联合反演大地电磁和接收函数的有效性，大地电磁模型分辨率得到一定提升.本文的算法不仅能够维持模型本身足够的自由度，又能够最大程度地获取耦合的速度模型和电阻率模型.

联合反演算法非常适用于识别高阻体中的低阻夹层，这种异常可能被围岩的高阻异常所淹没，很难通过单独反演得到低阻层的具体位置，而联合反演可以利用速度模型有效识别；对于高阻夹层，联合反演效果不如对低阻异常约束明显，但总体上优于单独反演结果；联合反演可以有效地约束出异常体的边界，相比于单独反演分辨率有一定的提升.总的来说，借助地震模型的约束，联合反演可以一定程度上提高大地电磁在深部的分辨率.

在华北地区，选取了一个地震和大地电磁相邻台站的数据，进行了大地电磁与接收函数的联合反演.反演结果表明，联合反演得到的速度模型和电阻率模型相比于单独反演呈现出更加耦合的特征，特别是对于莫霍面的约束，这有利于深部构造的解释，且可以借助RMS-β曲线选取最优的β参数值，它同时也是速度模型和电阻率模型是否耦合的重要指标.此外，通过对联合算子演化过程以及两种模型空间梯度分布的综合分析，可以判断电阻率模型和速度模型的耦合程度，这有利于地球物理反演结果的综合解释.