三维正交各向异性孔隙介质震电波场数值模拟研究

穆纳尔丁·托合提， 王一博， 肖文交,， 周可法

1 中国科学院新疆生态与地理研究所， 荒漠与绿洲生态国家重点实验室， 乌鲁木齐 830011 2 新疆矿产资源与数字地质重点实验室， 乌鲁木齐 830011 3 中国科学院新疆矿产资源研究中心， 乌鲁木齐 830011 4 中国科学院大学地球与行星科学学院， 北京 100049 5 中国科学院地质与地球物理研究所, 北京 100029

0 引言

在含流体的孔隙介质中地震波和电磁波可以互相转换，即地震波在含流体的孔隙介质传播过程中可以产生电磁波，同样电磁波在含流体的孔隙介质传播过程中可以激发地震波，这种耦合现象叫震电效应.震电信号的产生与介质物性参数密切相关，研究震电信号有助于了解震电效应的产生机理以及传播过程，具有重要的理论意义和实际价值.震电效应的研究最早可以追溯到1939年，苏联的Ivanov发现，在多孔介质中地震波可以引起电势变化(Ivanov，1939).随后Frenkel(1944)用动电理论解释了这种现象.后来Biot(1955，1956a，b)在Frenkel理论基础之上发展了一套孔隙介质中描述地震波传播的波动方程理论，为后来Pride震电耦合方程组的建立奠定了基础(Pride，1994).

目前有三种耦合的震电信号已经成为研究的热点(Wang et al.，2020)，分别是伴随震电信号(Haartsen and Pride，1997； Gao and Hu，2010)、界面震电信号(Haartsen and Pride，1997； Garambois and Dietrich，2002；Haines and Pride，2006；Thompson et al.，2005；Grobbe and Slob，2016)和隐式震电信号(Ren et al.，2016a).作为局部响应，伴随震电信号是由相对的固液运动引起的，并以与地震波相同的速度传播.当地震波遇到两种不同的多孔介质之间的界面或者多孔介质与另一种介质(例如流体)的界面时，会产生界面震电信号(Mikhailov et al.，1997),并以高于地震波的速度传播.Ren等(2016a)发现，地震波在含流体的层状孔隙介质中，除了产生伴随震电信号和界面震电信号之外，还会产生一种新的电磁波叫隐失电磁波(evanescent electromagnetic waves),当地震波传到界面且入射角大于临界角时，在界面处会产生隐式电磁波.隐式震电信号其实是当地震波以超过临界角入射产生的非均匀电磁波，本质上仍是界面震电信号，只是该非均匀电磁波不能向全空间任意方向传播了，只能沿着界面以相应地震波的速度传播，表现类似“同震信号”.Martner和Sparks(1959)通过野外实验研究了放在不同深度的爆炸源产生的震电信号，结果表明在地表可以观测到有一定埋深的分化层底部的界面产生的震电信号.严洪瑞等(1999)在我国的大庆油田做了野外试验，进行了震电勘探，成功地观测到了产生的震电信号，但是发现产生的震电信号信噪比较低，信号也比较弱.考虑到震电转换信号本身较弱且随着距离的增加呈指数衰减，有学者提出将接收点置于测量目标区域附近，即井中震电勘探的想法(陈本池等，2003；张元中等，2005).还有很多学者也进行了一系列野外和室内实验，主要验证了界面电磁波和伴随震电信号的存在(胡恒山等，2001；Garambois and Dietrich，2002；陈本池，2007；Bordes et al.，2006； Zhu et al.，2008，2016；Zhu and Toksöz, 2013; Schakel et al.，2011a，b，2012；Schoemaker et al.，2012； Bordes et al.，2006，2015；Roubinet et al.，2016；Butler et al.，2018；Peng et al.，2017，2019).

为了定量描述不同类型的震电信号的传播特征, Pride(1994)利用动电理论推导出了一组震电控制方程.控制方程组由两部分组成，分别是描述电磁波传播和扩散的麦克斯韦方程组和描述孔隙介质中弹性波传播的Biot方程组(Biot，1955，1956a，b).基于Pride模型，很多学者进行了一系列数值模拟和理论研究，探讨了不同介质中产生的震电波场特征，包括均匀介质(Pride and Haartsen，1996；Gao and Hu，2010；Ren et al.，2012；Slob and Mulder， 2016)、水平层状介质(Haartsen and Pride，1997；Garambois and Dietrich，2002；Jardani et al.，2010；Gao and Hu，2010；Gao et al., 2013a,b，2017a,b，2019; Jardani and Revil，2015；Ren et al.，2010，2016a，b；Zyserman et al.，2015；Grobbe and Slob，2016；Jouniaux and Zyserman，2016；Monachesi et al.，2018a，b)和井孔模型(胡恒山和王克协，1999；Guan and Hu，2008；Guan et al.，2013).Haartsen和Pride(1997)用数值方法确定了层状孔隙介质中点源的电震响应.Garambois和Dietrich(2002)基于Pride (1994)耦合方程给出了在层状饱和孔隙介质中震电耦合波场的模拟技术.Hu和Liu(2002)通过准静态近似方法，模拟了声电效应测井响应.Gao和Hu(2010)研究了剪切源在层状饱和孔隙介质中的震电波场响应.Haines和Pride(2006)基于有限差分算法，计算了准静态近似下层状孔隙介质的震电波场特征.考虑到震电波场中准静态近似会带来误差，Gao等(2017b)的研究工作对误差分析做了相应的探讨.Guan等(2018)基于准静态近似的数值模拟研究，分析了孔弹性波传播特征对震电波场的影响.Revil和Mahardika(2013)提出了另一震电耦合方程组，描述了在不饱和多孔介质中震电波场的传播，其与Pride的区别在于动电耦合系数L的表达式不同，耦合系数L依赖于净剩离子的含量.基于Revil和Mahardika(2013)的震电耦合模型，Save等人进行了数值模拟，探讨了震电耦合效应(Sava et al.，2014).

通过回顾国内外相关的研究进展，可以看到目前关于孔隙介质中的震电波场数值模拟研究主要是基于各向同性介质展开的，Tohti等(2020)之前做过有关各向异性孔隙介质中的震电波场数值模拟研究，但是只考虑了二维垂直对称轴的横向各向同性类型.为了更为全面地认识实际孔隙介质中产生的震电效应特征，需要开展三维正交各向异性孔隙模型的数值模拟研究.

本文是对我们之前工作的扩展(Tohti et al.， 2020)，研究了三维正交各向异性介质的震电耦合方程组，通过设计几种不同的正交各向异性模型，模拟震电信号在正交各向异性介质中的传播特征，分析了介质参数对震电波场的影响.

1 方法原理

1.1 各向异性介质震电耦合方程

基于Pride的控制方程(Pride, 1994)，Slob和Mulder在频率-波数域给出了三组基本方程(Slob and Mulder, 2016).它们分别是修正的麦克斯韦方程、运动方程和本构方程.在准静态近似下，我们可以将运动方程写成如下形式：

(1)

(2)

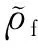
本构方程在时间域可以写成如下形式：

(3)

(4)

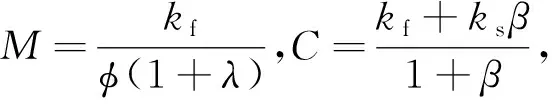
Slob和Mulder(2016)给出了如方程(5)所示的麦克斯韦方程组：

(5)

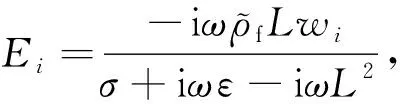
(6)

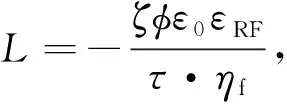
根据前人的研究结果 (Biot, 1956a,b; Carcione, 1996), 方程(1)—(6)在正交各向异性孔隙介质中可以写成如下形式：

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

1.2 震电耦合方程组有限差分离散格式

本文用有限差分算法对震电耦合方程组进行离散(Virieux, 1984; Tohti et al.，2020).用海绵吸收边界条件吸收边界上的反射波场(Petropoulos et al., 1998).根据以下原理，对方程(7)—(22)中的偏导数进行近似，

(23)

根据方程 (23), 可得到耦合方程组的有限差分离散格式如下:

(25)

+C1(x1,x2,x3)[w2(g3)-w2(g4)]+C1(x1,x2,x3)[w3(g5)-w3(g6)]]

(30)

+C2(x1,x2,x3)[w2(g3)-w2(g4)]+C2(x1,x2,x3)[w3(g5)-w3(g6)]],

(31)

+C3(x1,x2,x3)[w2(g3)-w2(g4)]+C3(x1,x2,x3)[w3(g5)-w3(g6)]],

(32)

×[v3(g3)-v3(g4)]],

(33)

×[v3(g1)-v3(g2)]],

(34)

×[v1(g3)-v1(g4)]],

(35)

×[v2(g3)-v2(g4)]+C3(x1,x2,x3)[v3(g5)-v3(g6)]+M(x1,x2,x3)[w1(g1)-w1(g2)]

+M(x1,x2,x3)[w2(g3)-w2(g4)]+M(x1,x2,x3)[w3(g5)-w3(g6)]],

(36)

(37)

(38)

(39)

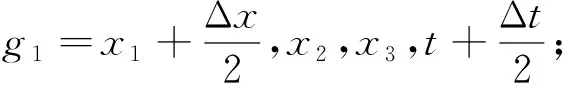
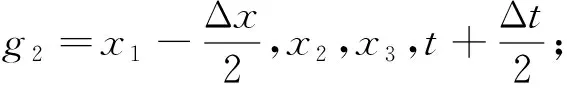
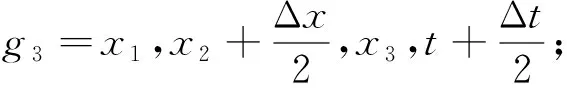
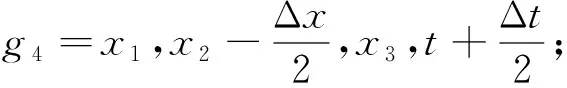
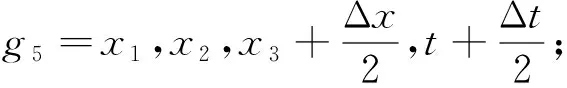
2 数值模拟

2.1 方法验证

为了验证我们数值模拟算法的正确性，第一步，将各向异性参数设置为ε1=ε2=0,δ1=δ2=0,γ1=γ2=0,δ3=0来模拟各向同性介质.

本文使用Slob和Mulder(2016)的3D解析解来验证了模拟代码，使用1 kHz Ricker子波作为震源时间函数，模型大小为624×624×624网格数，所有方向的网格间距均为0.1 m，时间步长为0.02 ms.我们将爆炸源置于模型的正中心，并在接收器R处接收信号.源和接收器的坐标如图1所示.

在所有模拟例子中，我们都对均匀介质进行了模拟.使用表1中的模型A的参数测试了代码.数值解与解析解的对比结果如图2所示.从对比结果可以看出，FDTD数值解与解析解基本吻合，这说明本文的模拟算法是正确的.

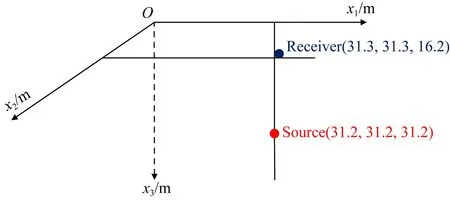
图1 接收器和源的坐标示意图Fig.1 Configuration of receiver and source location

图2 震电解析解和数值解之间对比 (a), (b), (c) 分别代表x1, x2和x3方向上的固体速度分量(V)； (d), (e), (f) 跟 (a), (b), (c)一样，但表示相对速度分量(W)； (g), (h), (i) 跟 (a), (b), (c)一样，但表示电场分量(E).Fig.2 Comparison between analytical solutions and numerical solutions of seismoelectric waves (a), (b), (c) represent the solid velocity (V) components on x1, x1, and x1 directions, respectively; (d), (e), (f) are the same as (a), (b), (c), respectively, but for filtration velocity (W) components; (g), (h), (i) are the same as (a), (b), (c), respectively, but for electric field (E) components.

2.2 数值例子

在本节中，我们分别模拟爆炸源在模型A、模型B、模型C、模型D、模型E和模型F中产生的震电响应.其中模型B、模型C和模型D只考虑了骨架的各向异性来分析骨架各向异性对震电波场的影响.模型F考虑弯曲度和渗透率的各向异性.我们将主频为1 kHz 的Ricker子波作为震源时间函数.模型尺寸为624×624×624网格数，空间步长为Δx=0.1 m，时间步长为0.02 ms.我们在源上方x2方向上布置了100个接收器，接收器与源位置之间的最小距离为15 m.

首先用各向同性模型A来模拟震电波场，模型A的参数如表1所示.图3中显示了在10 ms时刻的波场快照.我们观察到爆炸源在均匀各向同性多孔介质中激发两种类型的地震波.它们分别是快纵波(Pf)和慢纵波(PS).这两种波都产生伴随震电场.快速纵波类似于在弹性介质中产生的纵波.然而，慢纵波的传播特征取决于流体性质.慢纵波在流体黏度的影响下传播的慢，以静态模式出现在震源位置，如图3所示，其中EPf和EPs分别是Pf和Ps的伴随震电场.

为了研究震电信号在正交各向异性多孔介质中的传播特性，并分析流体黏度、固体骨架各向异性和弯曲度对震电波传播的影响，我们另外设置了具有不同参数的5种模型(标记为B到F)，如表1所示.

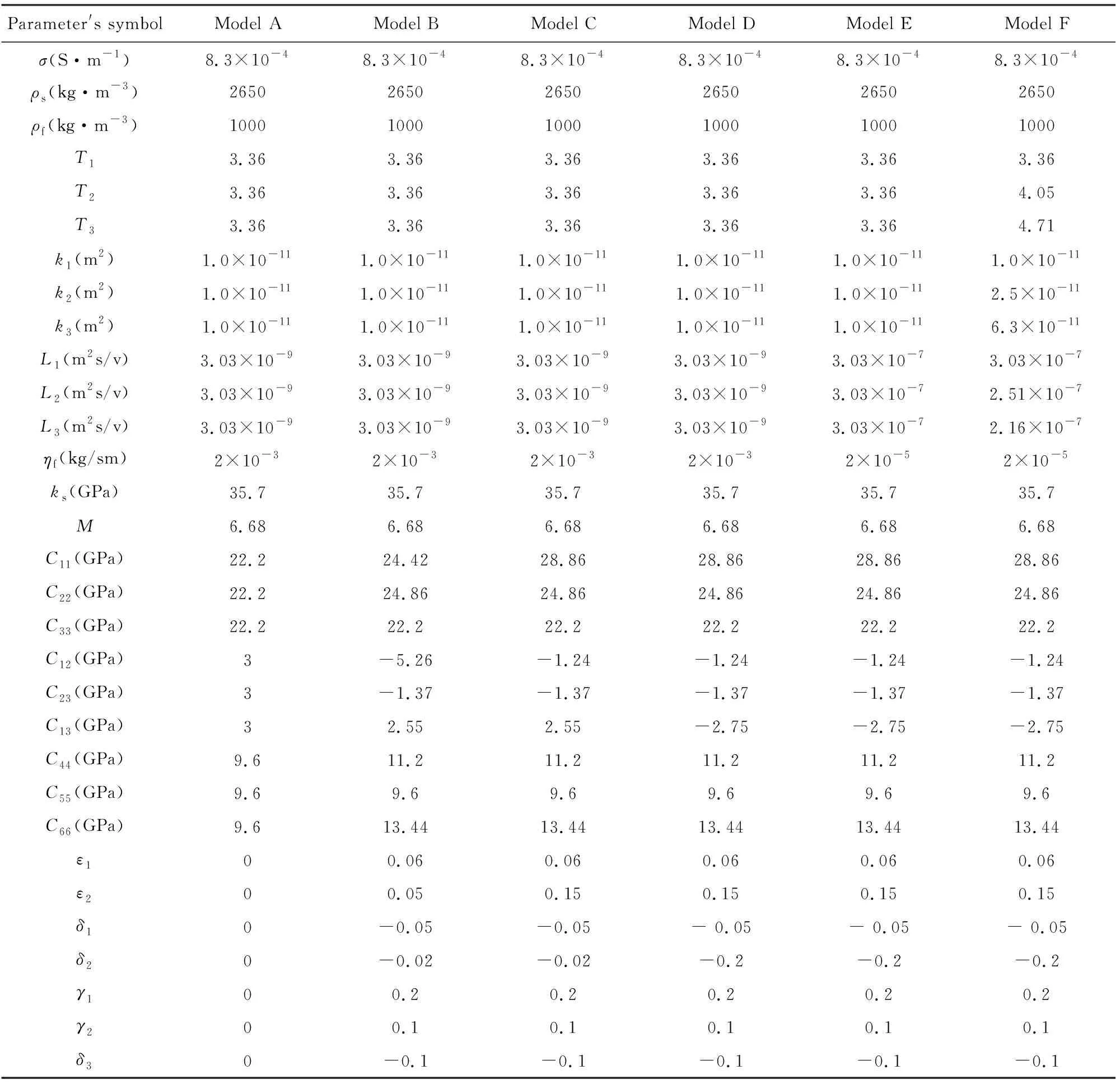
表1 在数值模拟中使用的模型参数Table 1 Model parameters used in numerical modeling

模型B与模型A的区别在于，模型A是各向同性的，而模型B是正交各向异性介质.我们在图4中显示了在10 ms时刻的模拟结果.可以观察到，除了快速波和慢速纵波外，爆炸源在各向异性孔隙介质中还会产生横波(S)(Ben-Menahem and Sena, 1990；Ben-Menahem et al., 1991).我们发现，波的各向异性在不同的平面上是不同的.存在[x1,x2]平面中的快S波和慢S波.ESf和ESS分别代表快和慢S波的伴随震电场.

为了分析固体骨架各向异性对震电信号传播的影响，我们模拟了模型C的震电响应.与模型B相比，模型C中各向异性参数ε2的值增加了，可以分析参数ε2对震电波场传播的影响.根据正交各向异性介质的定义，我们知道ε2控制[x1,x3]平面中波场的各向异性，而ε1控制[x2,x3]平面中波场的各向异性.因此我们只需要关注[x1,x3]平面中波场的变化就能分析出ε2对波场传播的影响.在10 ms时刻的模拟结果如图5所示.从图5中可以看到，在模型C产生的 [x1,x3]平面中的Pf波比模型B在 [x1,x3]平面中的Pf波显示出更大的各向异性效应.这说明各向异性参数ε(ε1,ε2)的值主要控制Pf波的各向异性(Tsvankin,1997; Wang et al., 2018).由于在模型C中ε2的值大于ε1的值，因此在模型C产生的[x1,x3]平面中的Pf波比模型C在[x2,x3]平面里的Pf波表现出更大的各向异性.

为了分析δ对震电信号传播的影响，我们模拟了模型D的震电响应.模型D与模型C的区别在于，模型D中的δ2值发生了变化.在正交各向异性介质中，我们知道δ2和δ1分别控制[x1,x3]和[x2,x3]平面里波场的各向异性，而δ3控制[x1,x2]平面里波场的各向异性.因此我们只需要关注[x1,x3]平面中波场的变化就能分析出δ2对波场传播的影响.图6显示了10 ms时刻的波场快照.我们观察到两种横波(S)在[x1,x3]平面中彼此分离了，换句话说，在[x1,x3]平面中的S波是在δ2的作用下分裂了，而在[x2,x3]和[x1,x2]平面中横波的变化不大，因为δ1和δ3的值没有发生变化.由此可以确定δ(δ1,δ2,δ3)对S波的各向异性的影响要大于对Pf波的影响(Wang et al., 2018).由于δ1,δ2和δ3的值不同，在模型B、模型C和模型D中产生的S波在不同平面上表现出不同的各向异性.

为了分析流体黏度对震电信号传播的影响，我们模拟了模型E的震电响应.模型E与模型D的区别在于，模型E中的流体黏度值减小了.在10 ms时刻的模拟结果如图7所示.我们观察到慢纵波(PS)及其伴随震电波(EPs)开始在介质中传播，换句话说，当流体黏度值减少时，慢纵波开始以传播模式出现了.由此证实了流体黏度对慢纵波及其伴随震电场的传播有较大的影响，当流体黏度降低时，慢纵波的传播速度增加.

最后，我们模拟了模型F的震电响应，以分析弯曲度对震电波传播的影响.模型F和模型E的区别在于，在模型F中弯曲度是各向异性的.由于耦合系数与弯曲度有关，耦合系数也是各向异性的.从Guo(2012)中可以看出，弯曲度和渗透率之间存在相关性，因此模型F中的渗透率也是各向异性的.图8显示了10 ms时刻的模拟结果.我们观察到，慢纵波及其伴随震电波(EPs)的波场快照形状显示为椭圆形，尤其是在[x1,x3]平面中，而模型E的模拟结果中慢纵波的波场快照显示为圆形.由此可以确定，弯曲度对慢纵波及其伴随震电场的传播有影响.慢纵波在[x1,x3]平面中具有更大的各向异性，这是因为x1和x3方向之间的弯曲度差异大于其他方向之间的差异.

2.3 运算效率

本文用Open Mp将FDTD代码并行化，在15 ms的模拟时间下用不同网格数和线程数测试了并行计算的性能.表2中给出了模型大小和线程数.基于表2，可以分析加速比和计算时间随着线程数的变化.

图9显示了不同模型大小和线程数下的加速比和运行时间.我们观察到，随着线程数量的增加，运行时间减少，加速比增加.

表2 不同模型大小和线程数下的运行时间Table 2 Run times for different model sizes and different number of threads

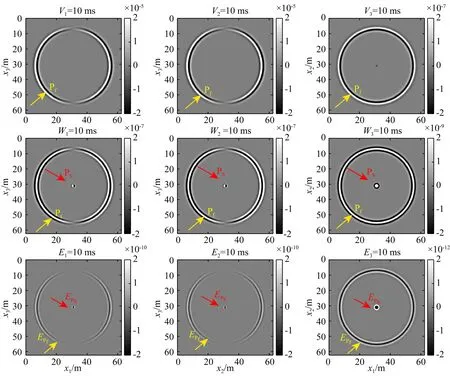
图3 模型A的震电波场快照Fig.3 Seismoelectric snapshot of Model A

图4 模型B的震电波场快照Fig.4 Seismoelectric snapshot of Model B

图5 模型C的震电波场快照Fig.5 Seismoelectric snapshot of Model C

图6 模型D的震电波场快照Fig.6 Seismoelectric snapshot of Model D

图7 模型E的震电波场快照Fig.7 Seismoelectric snapshot of Model E

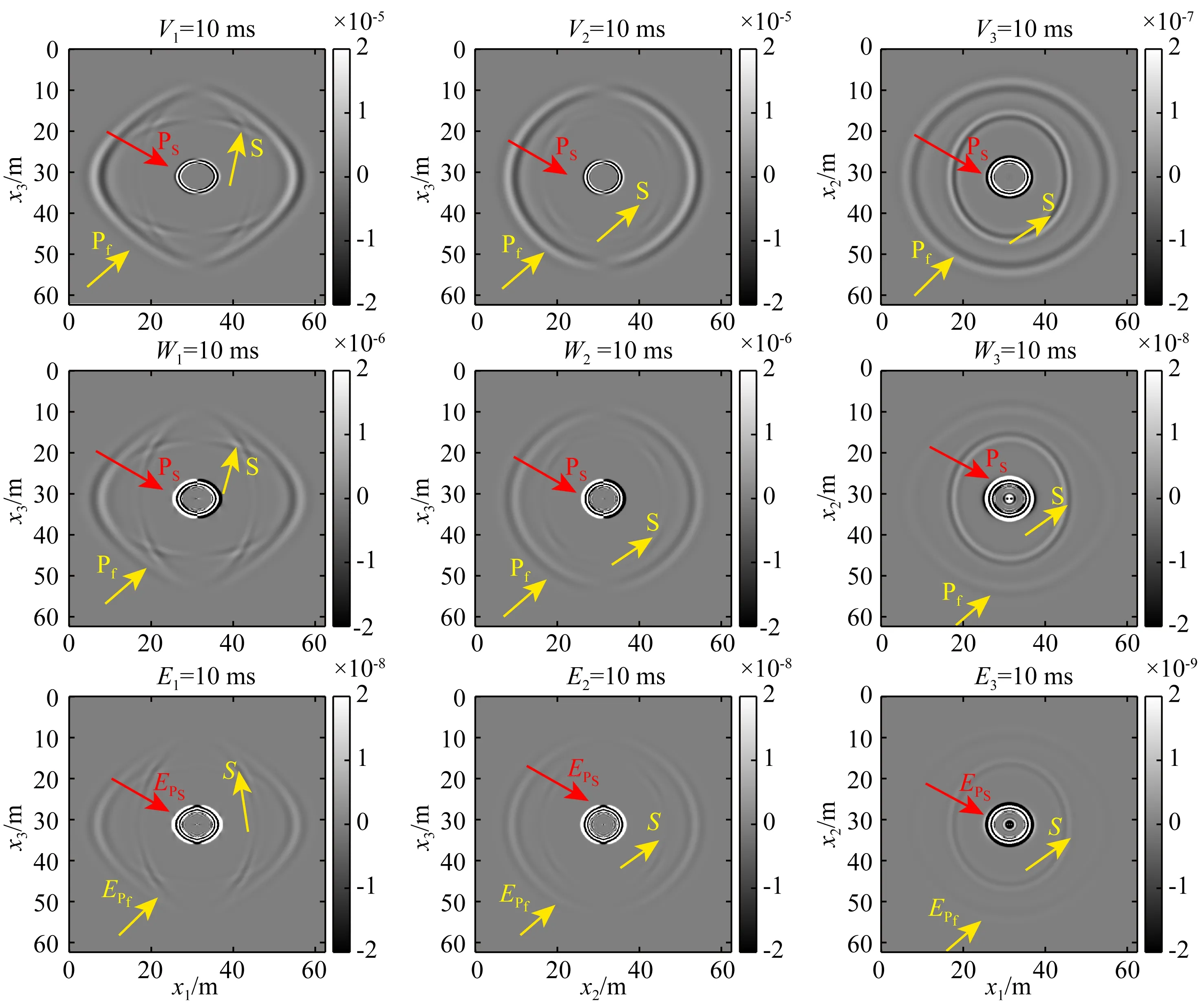
图8 模型F的震电波场快照Fig.8 Seismoelectric snapshot of Model F

图9 在不同模型大小和不同线程数下的运行时间(a)和加速比(b)Fig.9 Variation of run times(a) and speedup (b) with the number of threads for different model sizes

3 结论和认识

本文研究了各向异性孔隙介质震电耦合方程组，推导了三维正交各向异性孔隙介质情况下的时间域交错网格有限差分离散格式，模拟了爆炸源的震电响应，分析了介质参数对震电信号的影响，得出了如下结论.

(1) 爆炸源在正交各向异性的多孔介质中产生四种波，分别是快纵波(Pf)，慢纵波(PS)和两个可分离的横波.这四种地震波在均匀的多孔介质中都能产生伴随震电场.流体黏度和弯曲度对慢纵波的传播有影响.在流体黏度的影响下，慢纵波缓慢传播.弯曲度各向异性时，慢纵波的波场快照形状呈椭圆形，而弯曲度各向同性时，慢纵波的波场快照形状呈圆形.Pf波和S波的各向异性分别对ε(ε1,ε2)和δ(δ1,δ2,δ3)的值更敏感.

(2) 本文使用海绵吸收边界条件来压制了人工边界上的反射波，边界条件有效地吸收了边界处的反射信号.

(3) 基于Open Mp将模拟代码并行化，发现并行效果明显使运算速度提高了.

致谢感谢编辑和两位审稿人的宝贵意见.