集装箱起重机模糊PID防扭控制研究

翟秀丽 曹旭阳 庞 鑫

大连理工大学 大连 116024

0 引言

岸边集装箱起重机（以下简称岸桥）作为海陆的重要物流交通枢纽[1]，通常由大小车运行机构、起升机构和俯仰机构组成，图1为岸桥示意图。集装箱吊具通过4个钢丝绳悬挂于小车下方，钢丝绳长度的改变可实现对吊具姿态的控制，而吊具的抓箱和放箱等动作的准确性直接影响整个装吊环节的效率。集装箱偏载、钢丝绳柔性及风力等因素均可导致吊具在货物的入库及出库时其定位存在摇晃及扭转。在吊装过程中，当小车已运动到预期位置的情况下，集装箱与集卡对接时，集卡不一定与起重机轨道平行，目前主要采用熟练的技术人员手工调整的方法，但此方法严重影响工作效率。在实际工作中，吊具存在6个自由度：绕x、y、z方向的平移与转动，如图2所示。而绕z轴的转动角度直接影响技术人员调整吊具的时间。所以，本文忽略吊具其他5个自由度的影响，着重研究角度的控制方法。

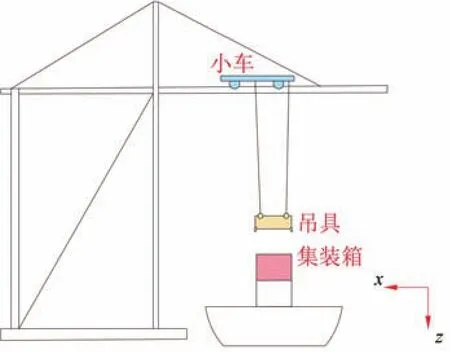
图1 岸桥示意图

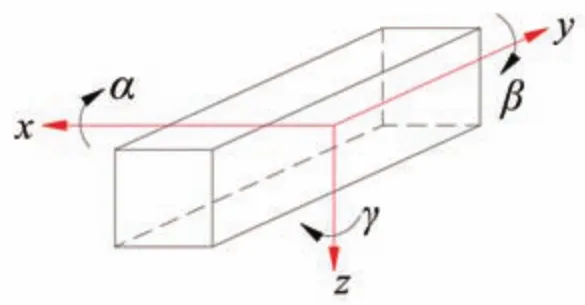
图2 集装箱吊具自由度示意图

在起重机的吊重摇摆控制方面已有许多学者进行研究。付林生[2]对起重机吊重的摇摆特性进行动力学分析，并进行实验验证；胡艳丽[3-5]等人将非线性优化方法与传统PID方法结合对起重机吊重进行控制；王华荣[6]针对桥式起重机提出一种基于粒子群优化的吊重防摆模糊PID策略；许多学者[7-9]主要研究吊重的位置控制，将起重机吊重视为质点，起升机构简化为单摆模型。而对于岸桥，吊具绕z轴的扭转角度对于实际抓箱与放箱的效率有着至关重要的影响，则吊具无法简化为质点进行研究。针对集装箱起重机，远天梦[10]利用牛顿迭代法对吊具扭转进行运动学分析，设计防扭系统并进行试验验证。目前针对集装箱起重机扭转控制研究较少，而吊具姿态角度控制直接影响吊运效率，故对集装箱起重机吊具防扭的研究具有重要意义。

以某厂RSH45S型集装箱吊具为分析对象，本文基于牛顿-欧拉方程对集装箱吊具的姿态进行动力学分析，研究模糊PID控制方法对集装箱吊具姿态角度γ的影响。通过实现PID控制参数的自整定，起重机吊具可有效减小扭转角度与扭转控制时间。

1 集装箱起重机系统建模

1.1 建立简化模型

集装箱起重机简化模型如图3所示，主要由小车、吊具、电动推杆、卷筒及滑轮钢丝绳等组成。吊具通过4组滑轮钢丝绳分别连接于小车上的4个电动推杆，电动推杆的伸缩可改变钢丝绳的长度进而实现对吊具姿态角度的调节。

在小车上建立坐标系A，在下方吊具处建立坐标系B，坐标系B随着吊具的位形时刻改变。吊具质心广义坐标为t=(x，y，z，α，β，γ)，其中：x、y、z分别为描述吊具相对于定参考基坐标系A位置的坐标值，α、β、γ分别为描述吊具相对于定参考基坐标系A姿态的卡尔丹角[11]。图3中，A点为钢丝绳与滑轮接触点，B点与C点为滑轮中心位置，对吊具进行受力分析，假设条件为：1）吊具质量和转动惯量不变；2）吊具几何中心与质心一致；3）重力恒定；4）每组绳索除AB与BC段的钢丝绳伸长量较小，忽略不计；5）滑轮尺寸较小，钢丝绳力作用点取滑轮中心处；6）滑轮两端钢丝绳力大小相等；7）钢丝绳简化为单向受拉的弹性体。

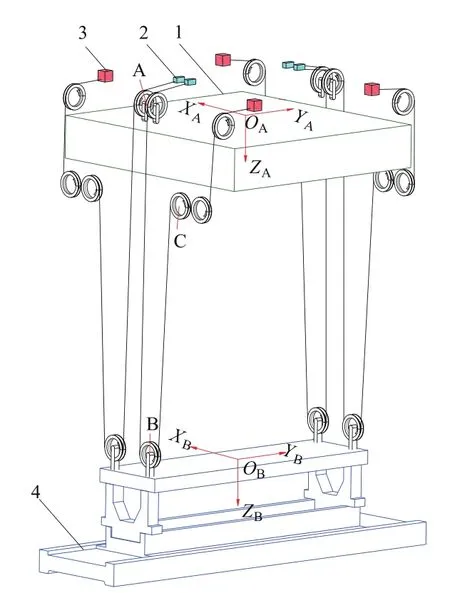
图3 集装箱起重机简化模型

综上所述，吊具受力简化为4组滑轮两端的AB与BC段钢丝绳拉力与自身重力。

1.2 钢丝绳拉力计算

对于钢丝绳拉力计算，将钢丝绳简化为单向受拉的弹性体，根据胡克定律，其拉力公式为

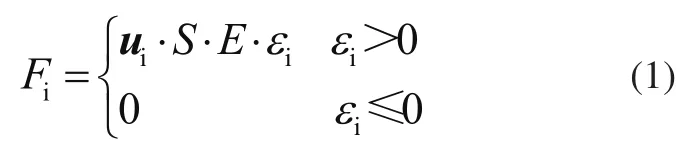
式中：ui为钢丝绳拉力方向向量，S为钢丝绳截面面积，E为钢丝绳弹性模量，ε1为钢丝绳应变量。

则

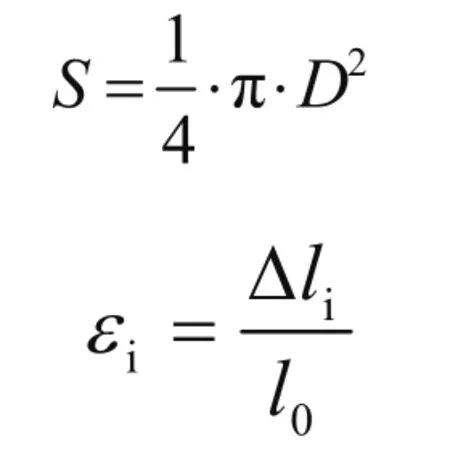
式中：D为钢丝绳直径。Δli为钢丝绳受力后的形变量，l0为钢丝绳原长。

在A坐标系下，ui钢丝绳拉力方向向量计算，以AB与CB段钢丝绳为例，有

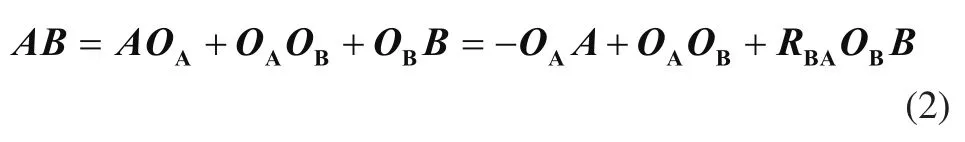
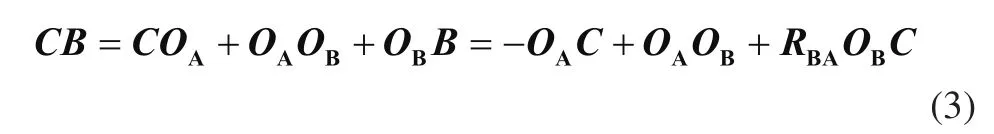
B坐标系到A坐标系的旋转矩阵为

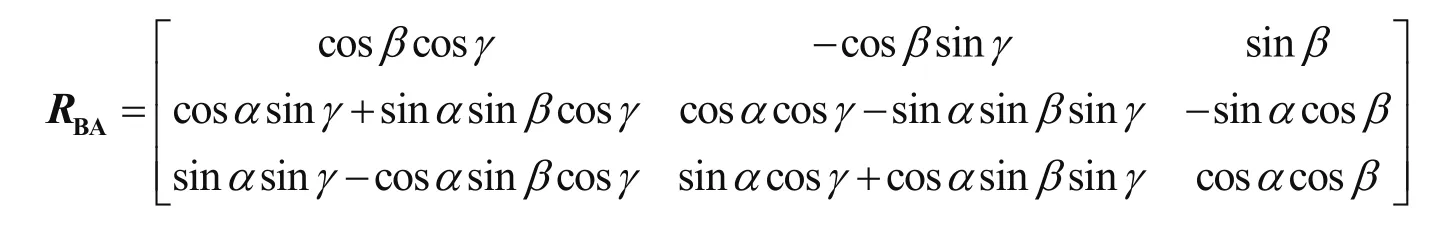
定义ui为在A坐标系中的钢丝绳的单位向量，则有

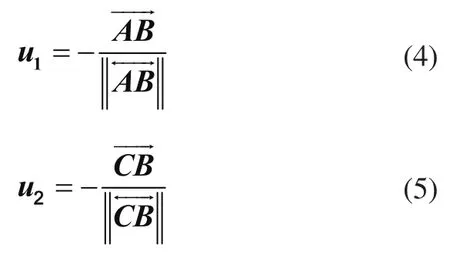
AB与CB段总形变量为

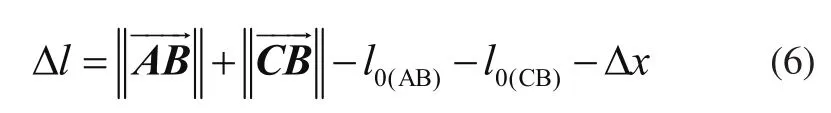
式中：为钢丝绳输入量。

AB与CB段形变量按原长比例分配的原则，则

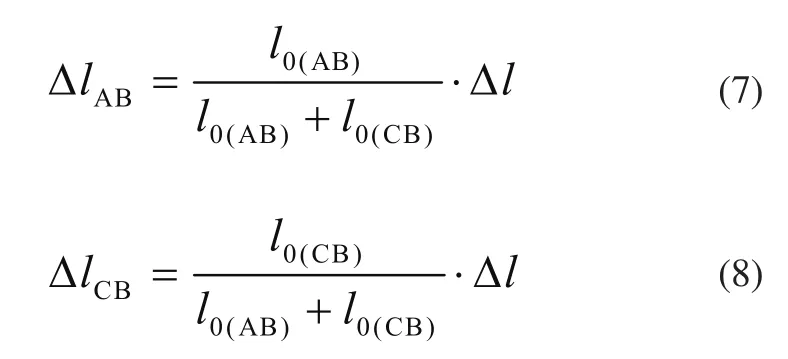
综上所述，可求出钢丝绳受力的大小与方向。同理，可求其余3组钢丝绳的受力大小与方向。

1.3 平移运动

假设吊具的受力为Fi(i=1，2，3，4，5，6，7，8)，产生的拉力总和用U1表示，方向为竖直向上，可得

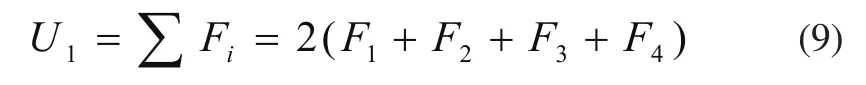
在A坐标系下，吊具的合外力可表示为

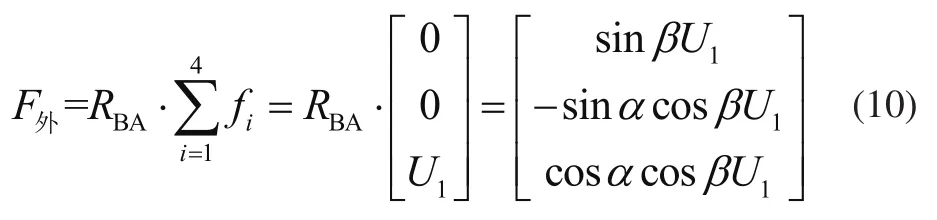
基于牛顿方程得吊具质心位置运动方程为

1.4 旋转运动

假设吊具的质心在吊具的几何中心处且保持不变，则吊具的惯性矩阵为

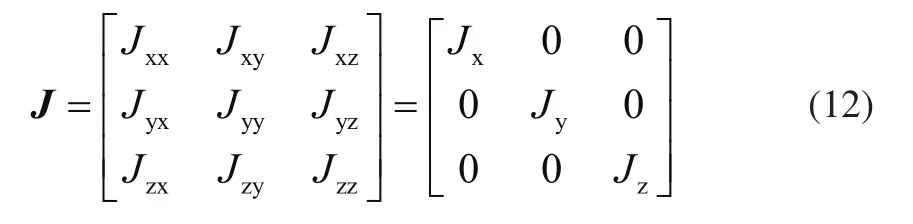
式中：Jx、Jy、Jz分别为x、y、z坐标轴的转动惯量。

利用刚体运动的欧拉方程表示吊具的旋转运动方程为

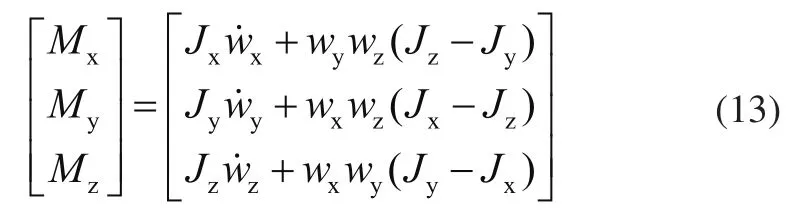
式中：Mx、My、Mz是吊具在3个坐标轴方向上的力矩分量。

卡尔丹角(α、β、γ)的变化率与吊具角速度的转换关系为

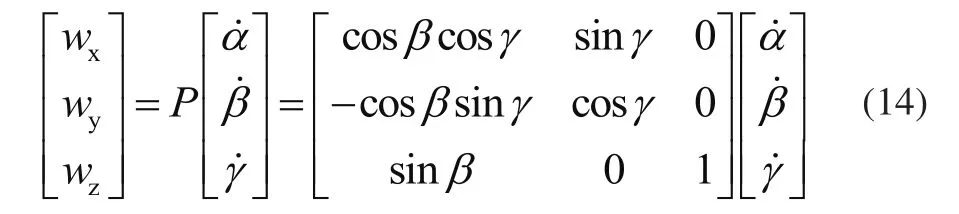
由于吊具的姿态角变化较小，式（14）可简化为

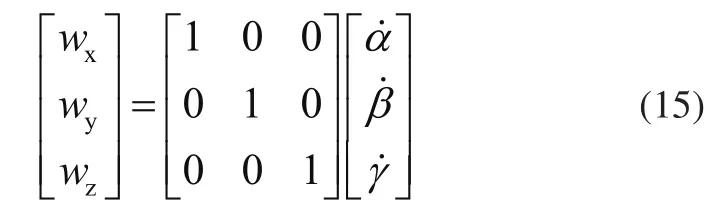
即卡尔丹角的变化率与吊具的角速度满足如下条件

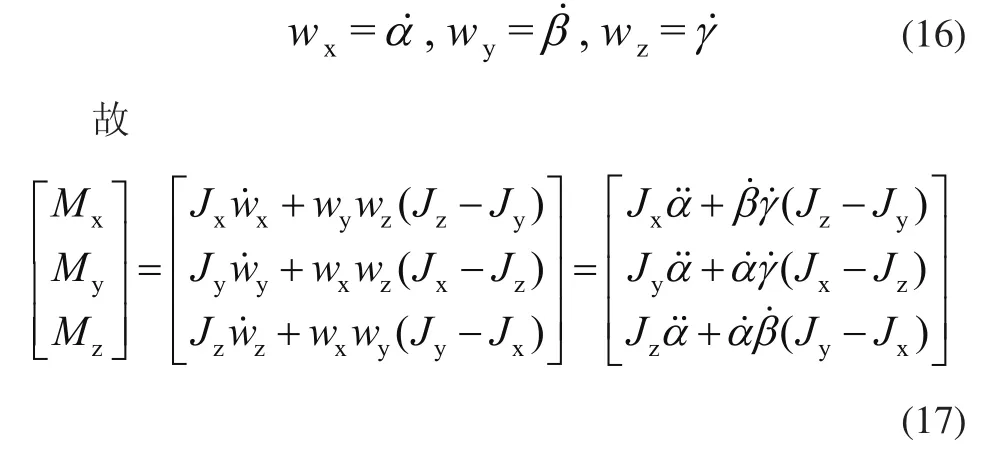
若U1、U2、U3、U4为控制量，则有

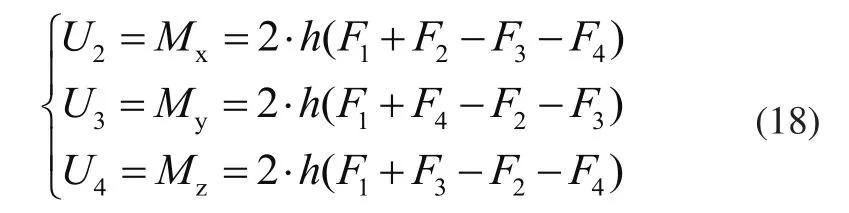
式中：h为钢丝绳拉力到吊具质心的距离。

控制量U1、U2、U3、U4与F1、F2、F3、F4之间的关系为

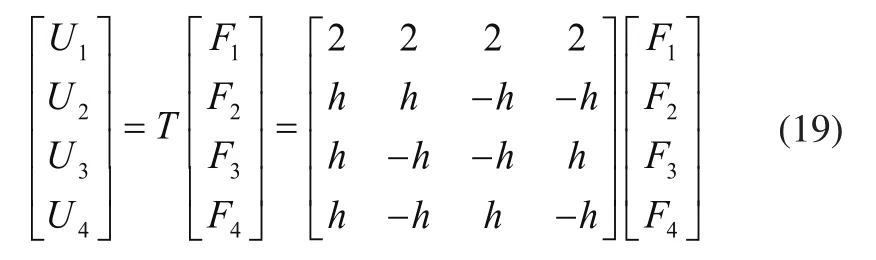
根据式（17）可求得吊具姿态角的运动方程为

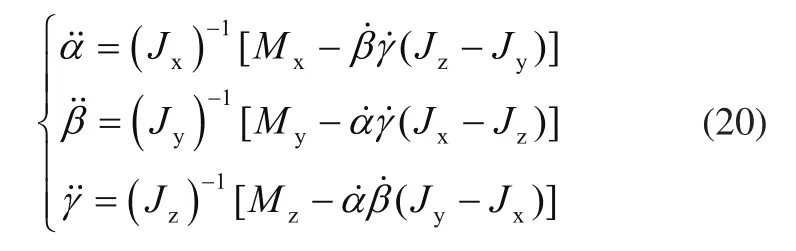
根据式（11）与式（20）可知，吊具的动力学方程为

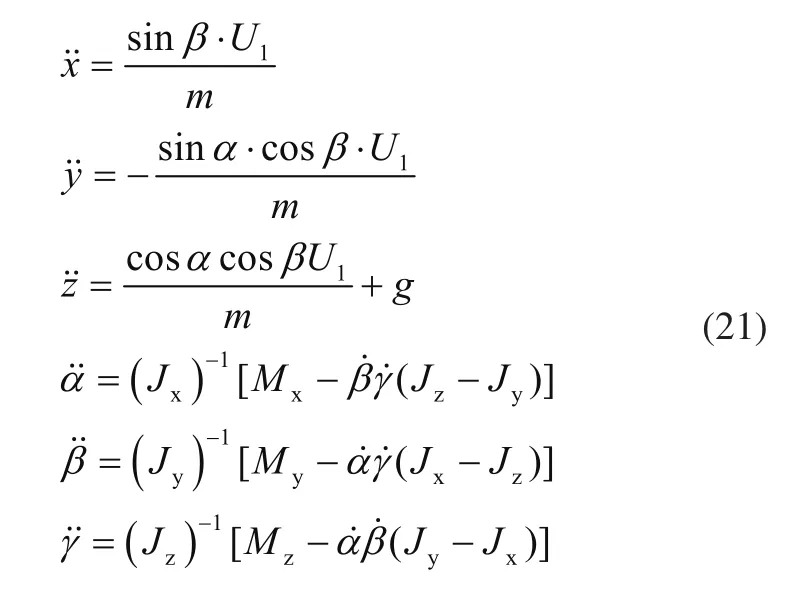
2 模糊PID控制算法

模糊PID控制算法的输入信号为参考角度与输出角度的差值E和差值E的变化率Ec，根据模糊控制规则，采用模糊逻辑对PID控制参数进行实时调整，相比于传统PID控制有着可实时整定PID参数的优点，图4为模糊PID控制原理图。模糊PID控制器的设计包含输入输出的模糊化、模糊控制规则的建立、模糊推理与逆模糊化4大步骤[12]。本文需设计4个模糊PID控制器分别控制电动推杆以改变钢丝绳长度进而控制吊具角度。

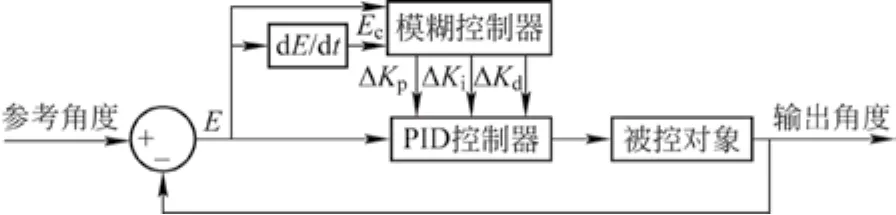
图4 模糊PID控制器原理图

2.1 模糊化

模糊化是将输入量与输出量进行模糊描述。首先是物理论域的量化，将物理论域转换为模糊论域称为量化。其次是建立模糊集合，此时的输入和输出量均为数值量，而通常要将输入量与给定值比较，通常将模糊集合等级设置为正大、正中、正小、零、负小、负中、负大，英文缩写为PB、PM、PS、ZO、NS、NM[13]。

基于上述理论，将集装箱起重机扭转角度控制系统的输入量与输出量进行模糊化，E、Ec、ΔKp、ΔKi、ΔKd设置为7个等级，计算量化与比例因子进行模糊化，其中一个模糊PID控制器的输入输出模糊化参数取值如表1所示，其他3个类似。

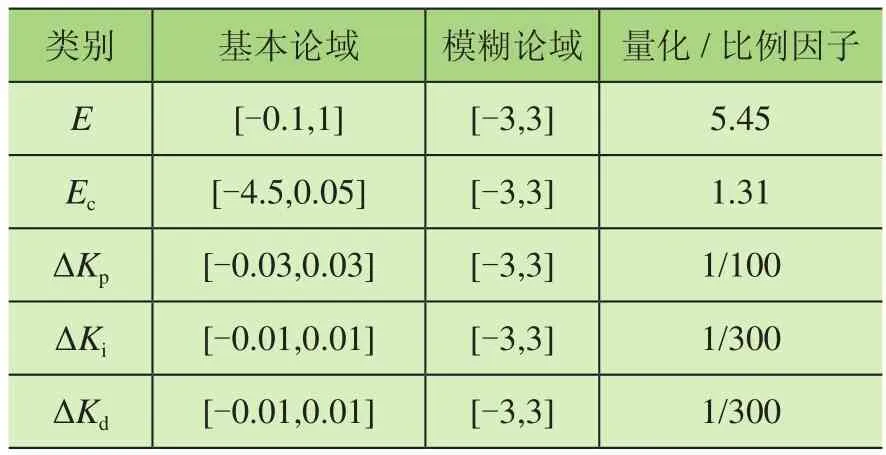
表1 输入输出模糊化参数

模型中输入量E、Ec与输出量ΔKp、ΔKi、ΔKd的隶属度函数如图5所示，选择高斯型函数。

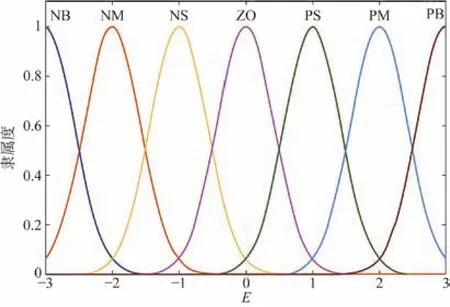
图5 E、Ec、ΔKp、ΔKi、ΔKd隶属度函数图

2.2 模糊推理

对于模糊PID控制器的设计来说，模糊控制规则的制定是算法的关键部分[14]。控制规则的制定多数基于实际工作经验，进而确定ΔKp、ΔKi、ΔKd3个输出量与偏差E、输入量偏差变化率Ec2个输入量之间的模糊规则。本文选用Mamdani直接推理法[15]，其与人类自然语言类似，通俗易懂，采用if…then…的书写形式，即：

IF (E is NB) and (EC is NB) then ( ΔKpis PB) ( ΔKiis NB) ( ΔKdis PS)

根据输入量E和Ec的不同组合，对应不同的ΔKp、ΔKi、ΔKd输出参数规则，2个输入量分别选择7个模糊变量，因此能确定49条模糊规则，如表2所示。

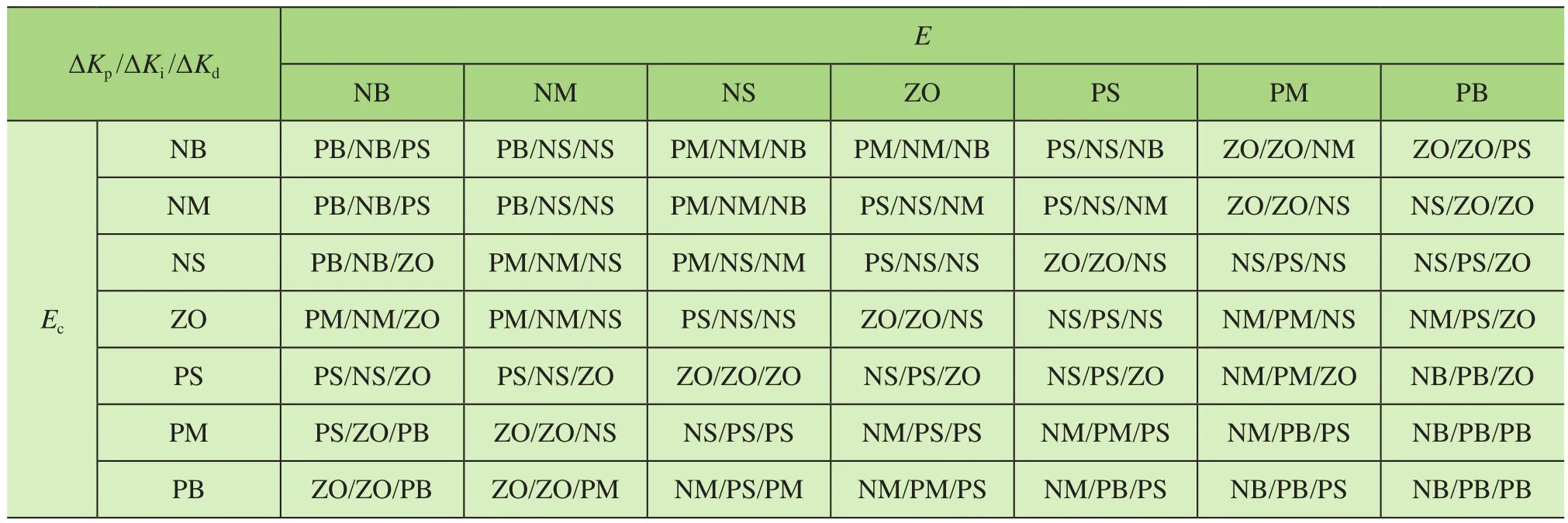
表2 模糊控制规则表

2.3 逆模糊化

在制定模糊规则后，对输入模糊量进行模糊推理，得到模糊输出量。经过逆模糊化处理可将模糊输出量转化为清晰的确定量。PID控制参数经过模糊推理后得到参数变化值，进行实现对PID控制参数的实时调节，则模糊PID控制参数为

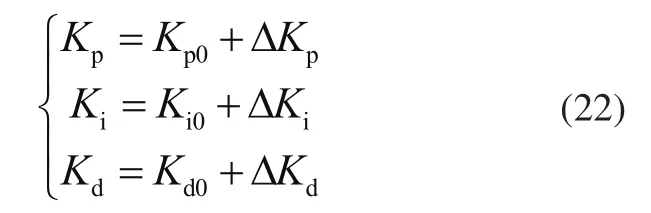
式中：Kp0、Ki0、Kd0为PID控制参数的初始值，ΔKp、ΔKi、ΔKd为参数的变化值。

3 控制系统设计及仿真

3.1 控制系统设计

利用系统建模得到的动力学方程，在Matlab Simulink中建立模糊PID控制器对系统进行控制。图6为模糊PID控制系统，其中模块1为4个模糊PID控制算法，可调节电动推杆的伸缩，即控制绳长的改变量，图7为模糊PID控制算法子系统；模块2为钢丝绳拉力计算模块，计算钢丝绳拉力大小与绳长改变量的关系；模块3为控制量与钢丝绳拉力转换，计算虚拟控制量与钢丝绳拉力的关系；模块4为吊具姿态角求解模块，返回输出角度实现闭环反馈控制。仿真参数设置为吊具质量m为15 300 kg；钢丝绳弹性模量E为10 GPa；钢丝绳直径D为14 mm；钢丝绳原长l0为11.7 m；重力加速度g取9.8m/s2。

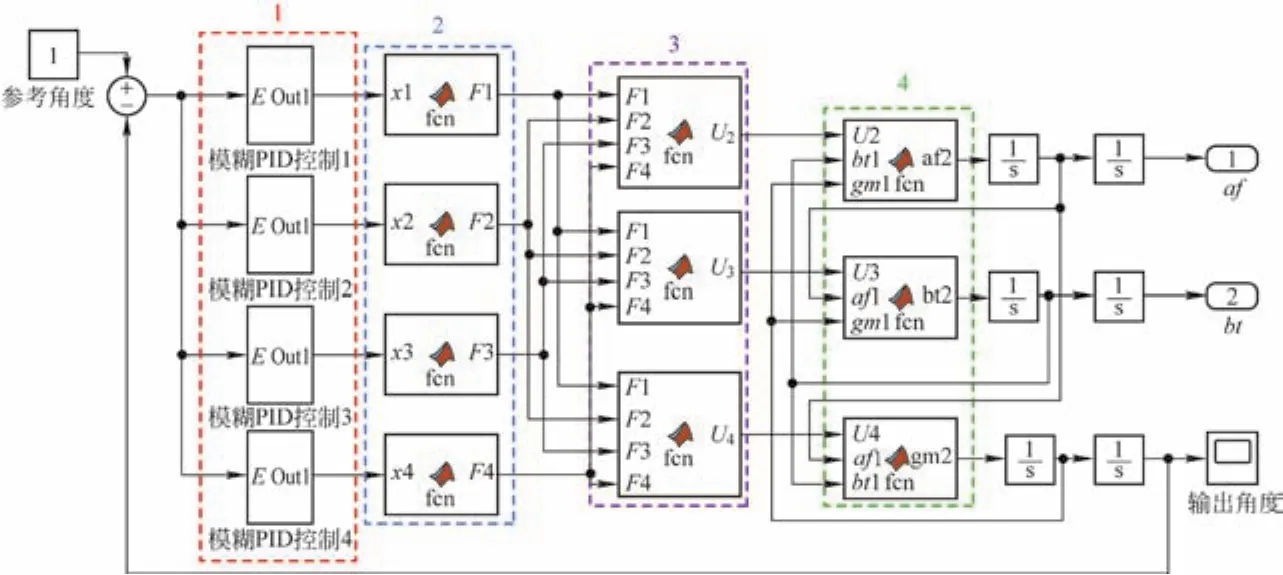
图6 模糊PID控制系统

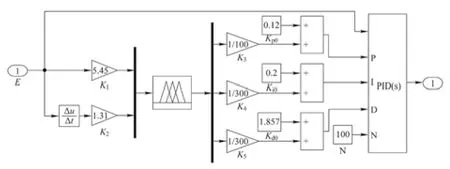
图7 模糊PID子系统

3.2 仿真结果分析

仿真结果如图8所示，黑色实线为无控制时的吊具扭转角度曲线，蓝色实线为模糊PID控制下的吊具扭转角度曲线。无控制时，吊具来回震荡，频率较高。角度的波峰出现在12.16 s，大小为1.392°；波谷出现在15.56 s，大小为0.926°。震荡周期约为0.6 s，幅度约为0.466°，稳态值约为1.16°，误差为16%。模糊PID控制时，吊具扭转角度曲线频率明显降低，角度的峰值出现在2.945 s，大小为1.079°；波谷出现在9.35 s，大小为0.927°。在响应速度上大幅度提升，稳态值约为0.97°，误差为3%。

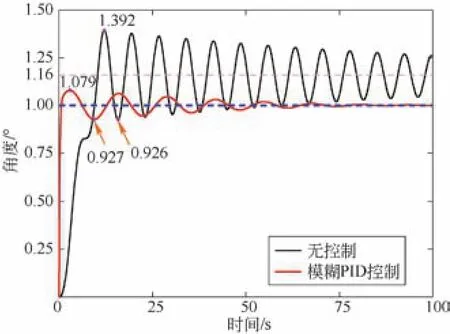
图8 角度对比图

传统PID控制方法的Kp、Ki、Kd确定后是不能改变的，模糊PID控制可完成控制参数的实时优化，动态更正系统的控制参数从而提高系统的鲁棒性。如图9所示，Kp、Ki、Kd参数随着控制系统的工况而实时变化，使吊具的扭转角度趋于稳定值。

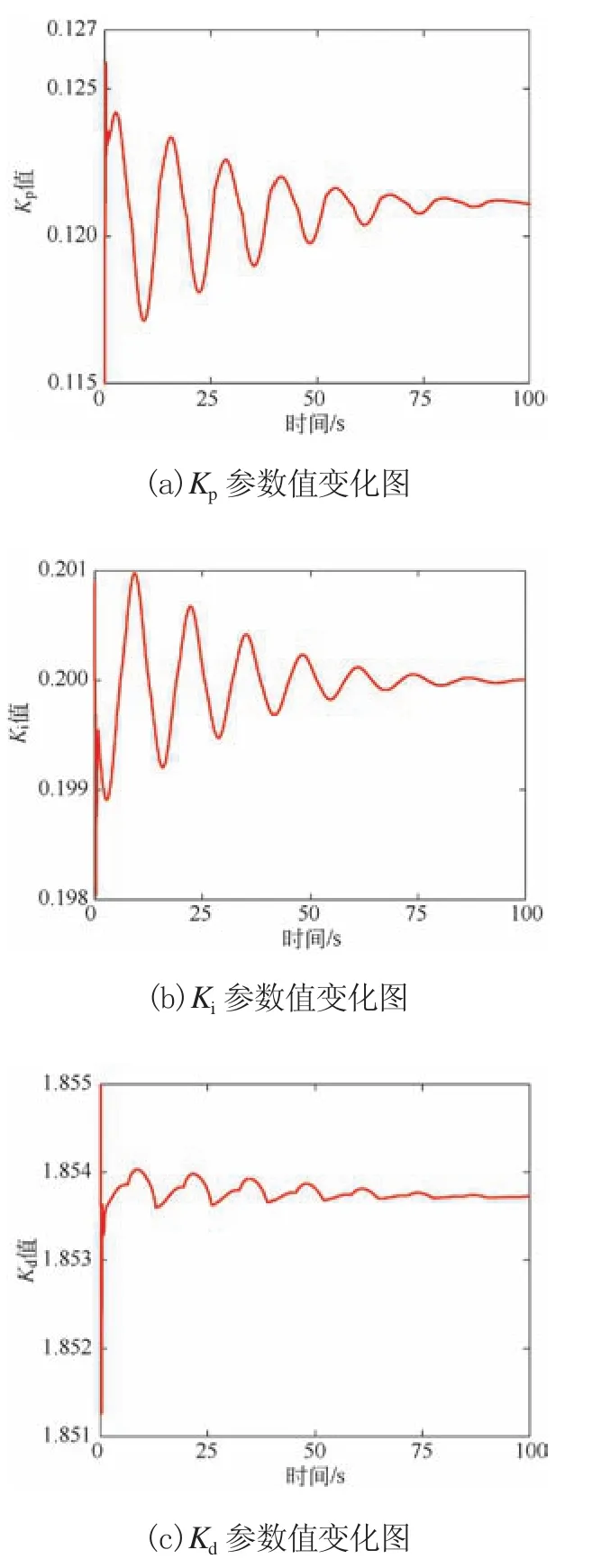
图9 Kp、Ki、Kd参数值变化图

3.3 模糊PID控制器鲁棒性分析

为验证模糊PID控制方法的鲁棒性，将系统参数绳长与吊具质量改变，进行仿真对比实验。将系统绳长改为10 m，系统其他仿真参数保持不变，仿真结果如图10所示。将系统吊具质量改为10 000 kg，系统其他仿真参数保持不变，仿真结果如图11所示。

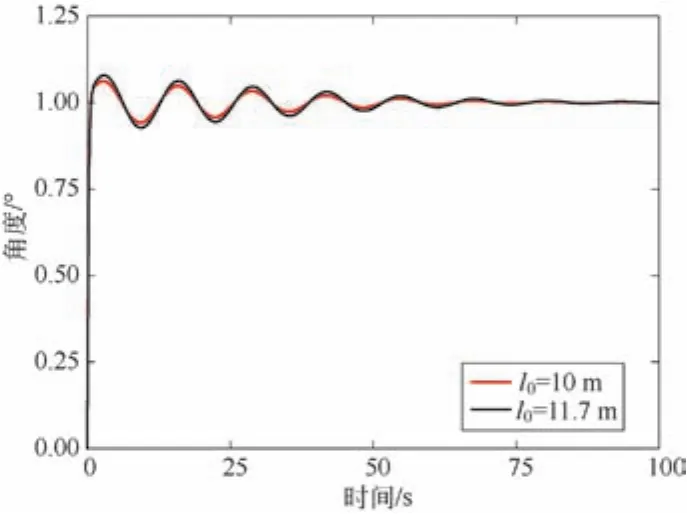
图10 角度对比图

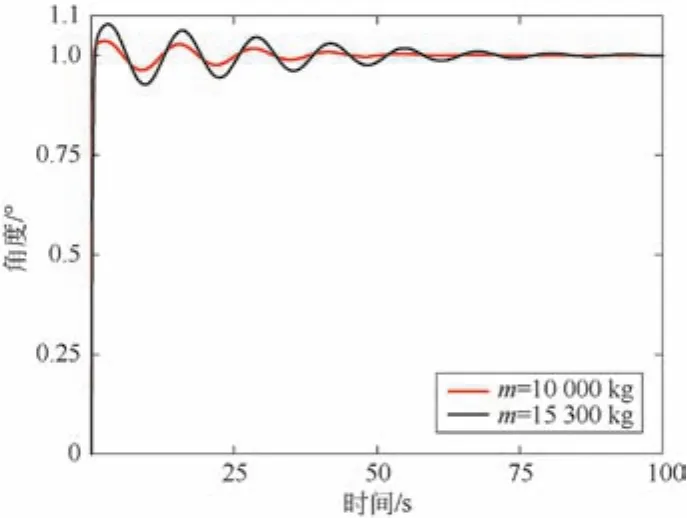
图11 角度对比图

4 结论

基于牛顿-欧拉方程对集装箱吊具进行动力学分析，推导出吊具位移及姿态角的动力学方程。设计模糊PID控制器及制定模糊控制规则，可实时整定控制参数。合理设置仿真参数后，仿真结果表明，与无控制相比较，吊具的最大扭转角度减少15.3%，峰值时间减少75.7%，稳态误差减少16.4%，系统的响应性能明显改善。改变系统的绳长与吊具质量时，模糊PID控制器适应性较强，系统可快速响应且扭转角度变化不大，证明系统的鲁棒性较强。本文提出的动力学方程及控制方法为岸桥吊具的自动化控制提供了理论依据。