基于改进Chebyshev的配电网工程造价合理区间分布研究

国网青海省电力公司经济技术研究院 田海丰 杨蒲寒婷 赵生延 国网青海省电力公司 赵健勃

配电网工程相对主网工程规模小且费用构成复杂，同时较主网工程缺乏相应的专业造价人员，使得其工程造价控制工作存在一定的难度。合理分析工程投资水平，有效控制工程造价是电网企业实现精准投资管控要求的重要手段。

造价合理区间是在历史工程数据的基础上得出的，用来判断某类工程造价水平是否合理的定量化控制方法，可用于初步设计阶段的设计评审环节。相比于传统的国家电网造价控制线和通用造价，合理区间考虑了地区差异，对不同地域因素及建设条件、差异化技术方案下造价具有良好的兼容性，能有效控制造价水平。

由此，如何精准确定造价合理区间受到学者广泛关注：姚刚[1]通过研究不同电压等级下的单位造价概率分布，定量计算其近似概率密度函数，进而得到输变电工程的造价区间；杜英[2]通过对比不同统计分析方法，将正态分布与四分位数间距法相结合，构造了造价区间的分析框架，通过实例确定工程造价控制区间；李泽阳[3]从造价大数据角度将正态模型、参数估计、拟合检验、区间估计等经典统计学理论相结合，构建了造价信息测算模型，并通过实例测算了某一置信水平下的造价区间。

以上学者通过构造不同数学模型以实现对造价区间的预测，但未详细划分样本种类、实际操作较为复杂，实践中有一定的局限性。本文参照国家电网典型造价划分样本类型，对相关样本集分别设立造价区间，通过一定的统计分析方法给出区间上限和下限，并与国家电网公司发布的造价控制线对比，验证区间合理性。造价合理区间可用以指导造价水平控制工作的顺利实施，且基于可靠数据，该方法可实现对不同技术方案下的配电网工程造价合理水平的分析，具有较强实用性。

1 配电网工程造价合理区间

本文选取2019～2020年青海省8个地市的配电网工程造价结算数据作为样本进行分析。其中配电工程247项、架空线路工程400项、电缆工程45项。参照《国家电网公司10kV 及以下配电网工程典型造价》工程划分思路对数据进行分类，为避免样本涵盖面不足，影响分析的真实性与合理性，对于仅存在1年数据且样本数量少于5项的工程类别，不列入本文的研究范围。综上，配电工程分为4种技术方案，架空线路工程分为6类技术方案，电缆线路工程分为6类技术方案。

1.1 配电网工程造价合理区间定义

本文结合专家经验及相关文献，定义至少有80%的样本数据落入的区间为该技术方案下的配电网工程造价合理区间，即在考虑地区、技术指标差异的情况下，表示为该地区待建配电网工程的合理造价水平。

1.2 配电网工程造价合理区间计算步骤

样本数据分类：参考《国家电网公司10kV 及以下配电网工程典型造价》工程划分思路，将近两年配电工程样本数据按照“变压器容量”一项指标进行分类，架空线路工程按照电压等级、导线类型、导线截面积三项指标进行分类，电缆线路工程按照电压等级、电缆材质、导线芯数×截面积三项指标进行分类；计算该类型样本数据的中位数、第一四分位数和第三四分位数，分别计算出该组数据的最大值和最小值，进而测算样本数据的样本均值和方差[4]；利用箱线图法剔除样本中的异常值。剔除异常值后样本数据更为科学、合理，本项工作为下一步进行区间计算提供了基础数据[5]。

利用改进Chebyshev 不等式，确定将有80%的样本数据将会处于合理区间中，即Φi={xij|μikiσi≤xij≤μi+kiσi}，式中：Φi 为配电网工程第i 类技术方案下的合理区间；xij为第i 类技术方案下的第j 个数据；μi为第i 类技术方案下的样本均值；ki为经迭代后第i 类技术方案下的区间系数；σi为第i 类技术方案下的样本标准差。

2 配电网工程造价合理区间计算理论介绍

2.1 箱线图理论

箱线图是利用数据中的五个统计量：最小值、第四分位数、中位数、第三四分位数与最大值来计算一组数据分散情况的数学算法。箱线图判断异常值的标准是以四分位数和四分位距为基础，四分位数具有一定抗干扰性，多达25%的数据可变得任意远而不会在很大程度上干扰四分位数，这样使异常数据识别结果更加客观。其公式为：

式中：QLi为配电网工程第i 类技术方案下的数据第一四分位点；QUi为第i 类技术方案下的数据第三四分位点；QIQRi为第i 类技术方案下的四分位数间距，为QLi与QUi两数之差；QBLi与QBUi为配电网第i 类技术方案下数据检测下界与检测上界。当第i 类技术方案下的数据小于检测下界QBLi或大于检测上界QBUi时，认为该值属于异常值。

2.2 改进Chebyshev不等式理论

Chebyshev 理论由19世纪俄国数学家切比雪夫提出。根据该理论，计算一个样本数据集的平均值及方差，可得到在一定比例条件下该样本数据集的区间分布。由于切比雪夫对于样本数据集的普遍适用性，依据该理论研究会得到一个非常保守、粗糙的上下界。因此，本文在引入Chebyshev 理论的基础上，采用成功失败法优化参数，提升造价波动性大特点下的造价合理性及控制能力。对于处于任意一种分布形态的样本数据，由Chebyshev 不等式可知，将有至少以概率P 数据处于k 个标准差范围内，即任意一个数据集中，位于其平均数k 个标准差范围内的比例总是至少为1-1/k2：Pi{xij|μiki0σi≤xij≤μi+ki0σi}=1-1/ki02。

式中：ki0为第i 类技术方案下的区间初值；Pi为配电网工程第i 类技术方案中的数据落入初始区间Ωi={xij|μi-ki0σi≤xij≤μi+ki0σi}的概率。当1-1/ki02=80%时，可得区间初值ki0=2.24。如计算得到的区间包括了80%以上样本数据，则可通过调整区间初值ki0，使得造价区间趋于80%左右的样本数据，即本文所提出的造价合理区间。

本文使用成功失败法为参数寻优的方法，对区间初值k 进行一维无约束条件的迭代寻优。成功失败法以区间初值ki0为迭代对象，以某一技术方案下落入合理区间的样本数量占总样本的比例与80%的差值作为寻优函数，即认为当该函数值无限接近0时，合理区间内包含的样本数量愈趋近80%，此时的区间即为造价合理区间。寻优迭代从区间初值ki0=2.24开始反复搜索，直至找到目标函数的一维无约束条件寻优函数极小值minFi(k1)，迭代寻优结束，并得到区间参数ki。寻优目标函数为：minFi(k1)=|num(μi-ki0σi≤xij≤μi+ki0σi)/num(zi)-80%|。式中：ki为配电网工程第i 类技术方案下的区间参数；minFi(k1)为带入ki后第i 类技术方案的寻优函数极小值；num(μi-ki0σi≤xij≤μi+ki0σi)为第i 类技术方案下落入区间μi-ki0σi≤xij≤μi+ki0σi的样本数量；num(zi)为第i 类技术方案下的样本总数。

综上，本文利用MATLAB 仿真软件采用成功失败法对参数k 值进行迭代寻优。设初始步长h0=-0.10，精度ε=0.005，初值ki0=2.24，当搜寻结果为成功且步长|hi|＜ε 时迭代终止，得出最优解ki。

3 样本分析

为验证所提方法可行性，本文选取配电工程400kVA 变压器容量作为造价合理区间的样本进行分析，样本数据共计46项，其最大值为652.66元/kVA、最小值为140.71元/kVA，平均值为322.24元/kVA。

异常数据的剔除。计算400kVA 变压器容量配电工程中样本数据的第一四分位数QL1为268.37元/kVA，第三四分位数QU1为332.72元/kVA、四分位数间距QIQR1为64.35元/kVA。由式(2)计算箱线图检测上界QBU1为429.24元/kVA，箱线图检测下届QBL1为171.84元/kVA。根据箱线图理论剔除异常数据6项，剩余样本数量为40项，样本数据区间为[202.16,409.98]。此时400kVA 变压器容量配电工程技术方案下的样本均值μ1=293.69，样本标准差σ1=49.61。

区间系数k 寻优。利用成功失败法计算k1值，400kVA 变压器容量配电工程当迭代计算到68次时步长|h|＜ε，计算终止，得到k1=1.35，此时一维无约束条件寻优函数minF1(k1)=0.00%；测算造价合理区间。将参数k 代入式(1)中，得到400kVA变压器容量配电工程的造价合理区间下界μ1-k1σ1为226.76元/kVA，合理区间上界μ1+k1σ1为360.61元/kVA，则400kVA 变压器容量配电工程的造价合理区间为[226.76,360.61]。

区间合理性验证。为检验造价区间的合理性，本文参考《国家电网公司配电网工程通用造价10kV配电分册》，与其典型方案单位容量静态投资进行对比（图1）：经过与《国家电网公司配电网工程通用造价10kV 配电分册》中的400kVA 变压器容量配电工程典型方案单位造价对比，其所有典型方案的单位造价均在造价合理区间内，该项结果验证了造价区间的合理性，同时也说明了本文研究方法的可行性。

图1 400kVA 变压器容量配电工程与国网典型方案对比情况

各类技术方案造价合理区间。将该方法应用于其他各类技术方案下的配电网工程中，得到各技术方案下配电网工程造价合理区间，并与相应典型造价进行对比。结果表明，相应典型造价均能落入利用此方法所计算的造价合理区间内（表1）。

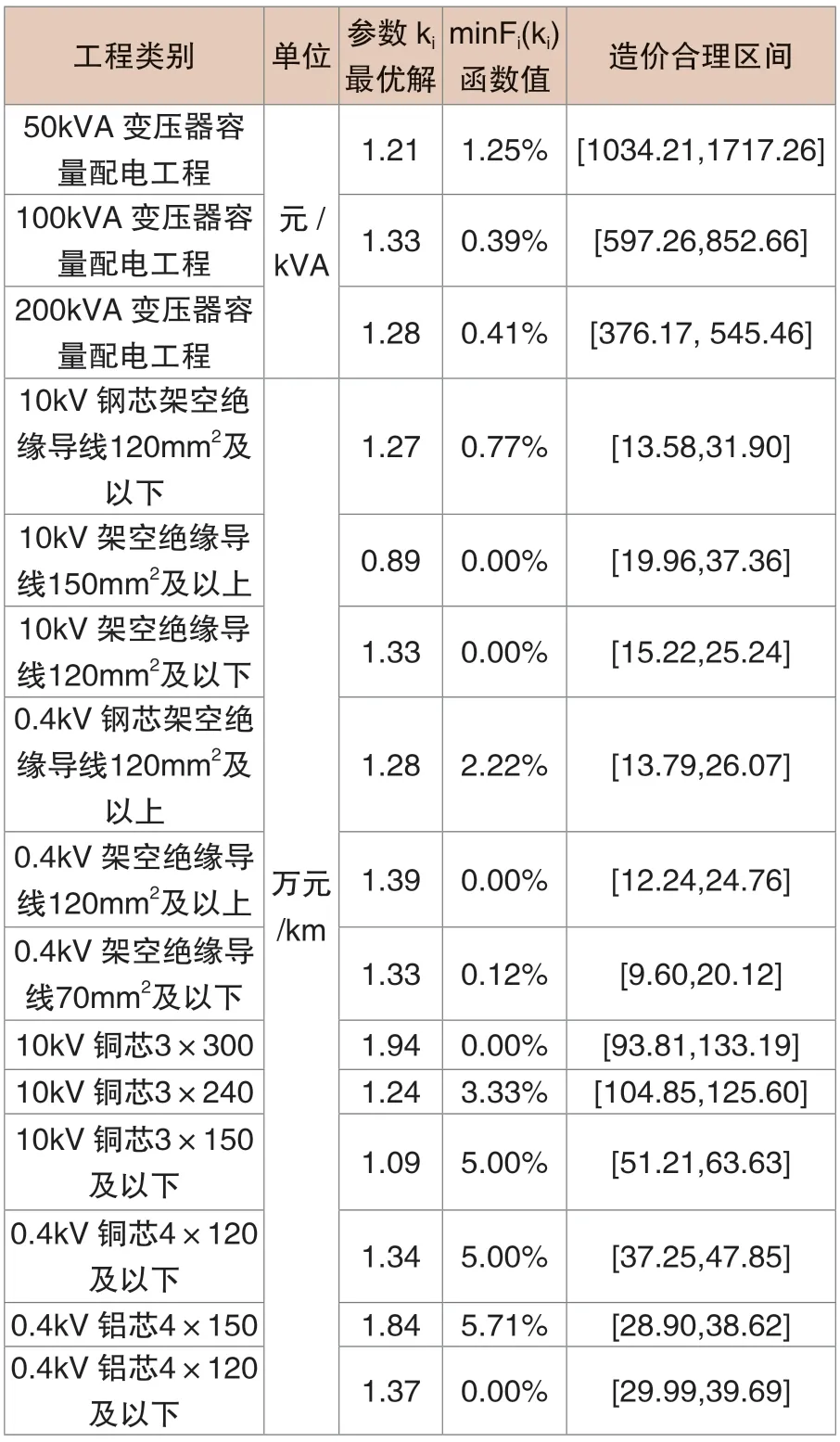
表1 其他技术方案下配电网工程造价合理区间

4 结语

综上所述，采用箱线图法剔除异常值的思想，可以作为实际工程数据分析的常用方法，对于消除异常数据所带来的噪声干扰有着一定的优势；当样本数据足够大时，该合理区间计算方法可得到较为有代表性的造价区间值，为各地区控制配电网工程造价提供可靠度较高的分析依据，具有较大的实际意义。