内啮合齿轮泵流体动态性能分析

王方涛，钟志豪

（200093 上海市 上海理工大学 机械工程学院）

0 引言

内啮合齿轮泵内部流体在工作状态下会产生相应的压力波动和流量波动，其对齿轮泵的升温、泄漏量等性能有重要影响。本文使用PumpLinx 齿轮泵仿真软件对齿轮泵内部流体动态性能进行三维数值仿真，建立计算流体域模型，设置边界条件和求解参数，得到齿轮泵内部流场的压力分布云图，并根据云图分析负载变化时对内部流体压力和齿轮泵流量的影响规律。

1 湍流模型

湍流模型为计算流体动力学（Computational Fluid Dynamics，CFD）中最基本的模型，基于流体动力学基本的控制数学模型建立。

（1）连续性方程。质量守恒方程是流体运动学遵循的基本定律之一，假设流体在运动过程中在系统中的质量保持不变。

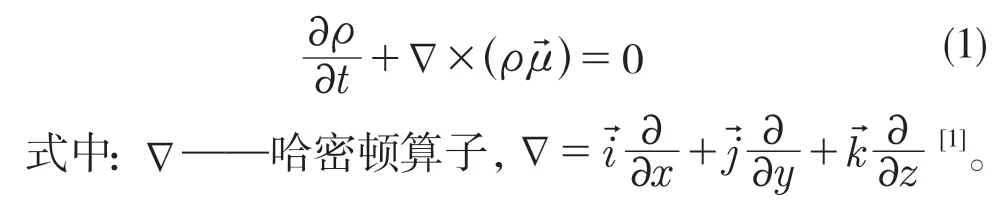
（2）运动方程。动量数学定律也是流体在运动时需要遵循的基本定律之一，对于其给定的流体系统，动量随时间的变化率与它所受外力总和相等，其数学表达即为运动方程[2]：

式中：ρfx——单位质量力在x方向上的投影；ρfy——单位质量力在y方向上的投影；ρfz——单位质量力在z方向上的投影；p——压力。

考虑到液压油是不可被压缩液体，它的密度和动力粘度为常数，可得：

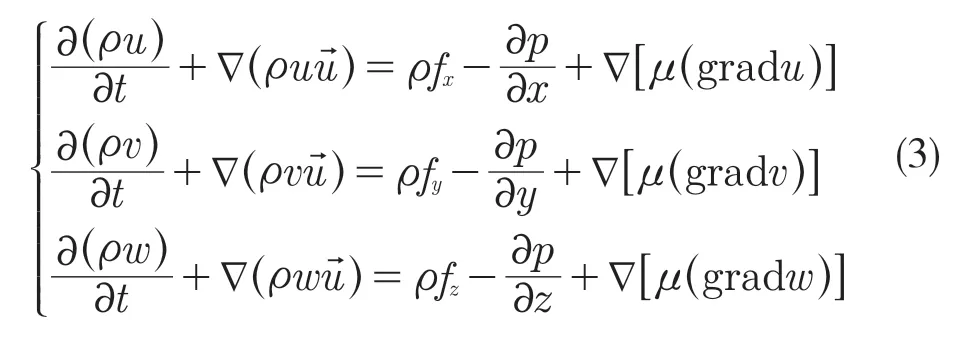
（3）能量方程。能量守恒定律适用于能量方程式，即流体从外界增加的能量等于外力对其做功和其他形式能量的输入。流体运动同样可以使用热力学第一定律，即是能量方程[1]。

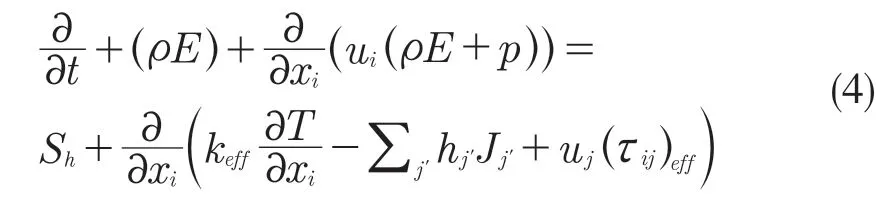
式中：E=；keff——有效热传导系数，Jj'——分组j的扩散能量；Sh——体积热源项。

目前在湍流模型中，k-ε模型使用最为广泛，主要分为Standardk-ε，RNGk-ε及Realizek-ε模型。其中；Standardk-ε的模型比较适合对完全湍流的液体流动过程进行模拟仿真；RNGk-ε模型主要针对高雷诺数流动问题；Realizek-ε模型应用范围比较广泛，主要针对流体流动时均应变率较大、可能出现负压的情况[1]。由于齿轮泵在高速高压工况下工作，其内部流场的流动情况较为复杂，流体会产生剧烈的旋转[1]。为了更精准地仿真计算齿轮泵的内部流体流动的精确情况，本次选择Realizek-ε模型进行仿真分析。

Realizek-ε模型湍动能及其耗散率输运方程为

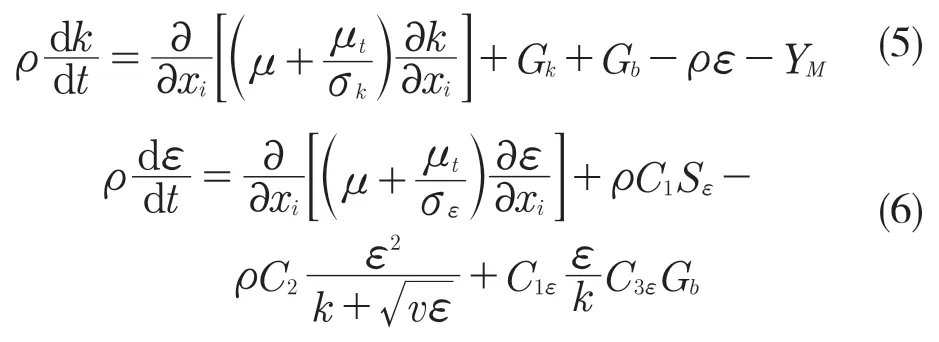
式中：C1ε，C2ε，C3ε，C2——常数，在PumpLinx 中，作为默认值常数，C1ε=1.44，C2ε=1.90，C3ε=0.09，C2=1.90；σk=1.0；σε=1.2[1]。

2 几何建模

本文根据渐开线齿形的齿轮设计制造的原理绘制齿轮泵内外齿轮齿形端面。内齿圈在齿根处开有径向通孔，在原理上消除了齿轮在啮合处会产生的困油现象，从而减少振动降低噪声[3]。根据绘制出的齿轮副齿形端面，如图1 所示。基于SolidWorks 软件建立齿轮泵齿轮副三维模型，与简化的月牙板进行配合，并检查是否存在干涉，

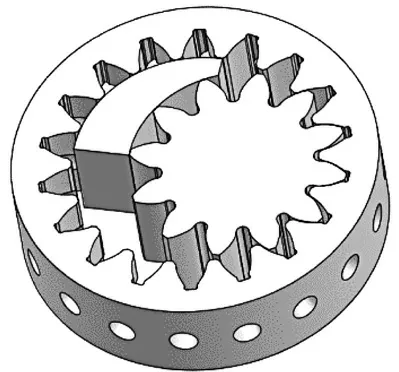
图1 齿轮副三维模型Fig.1 Three-dimensional model of gear pair

齿轮泵的泵体，前盖，后盖与齿轮副端面紧密配合成了齿轮泵内流体的工作区域，工作区域的剖视图如图2 所示。

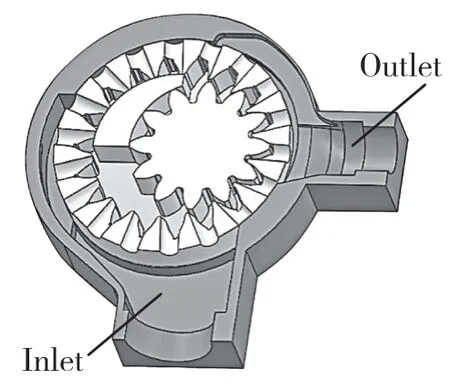
图2 工作区域的剖视图Fig.2 Section view of work area

齿轮泵计算流体域的几何参数：进油口直径32 mm，出油口直径18 mm，齿轮齿宽7.026 mm，外齿轮对应的齿顶圆直径58.5 mm，内齿轮齿顶圆直径52 mm，内外齿轮模数3.25，外齿轮齿数18，内齿轮齿数12，中心距10.5 mm，变位系数0.6，压力角20°。

对泵体内部的进油口和出油口进行模型提取，与内齿圈外部同轴心配合，可得齿轮泵流体域的计算模型，保存为.stl 格式文件导入PumpLinx 进行下一步的网格划分[4]。齿轮泵计算流体域模型如图3所示，计算模型分为进油区域（inlet）、出油区域（outlet）和齿轮副区域（gear）3 个部分。

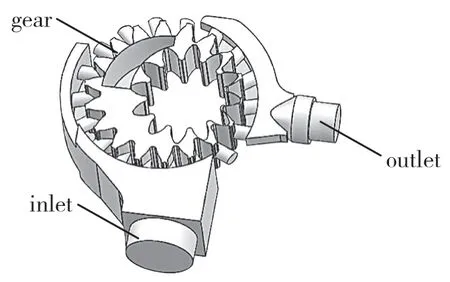
图3 齿轮泵计算流体域模型Fig.3 Computational fluid domain model of gear pump

3 流体域网格划分和响应面设置

网格划分使用PumpLinx 自带的自动化网格生成器，其采用CAB 算法，针对重要的三维几何结构，通过分裂网格自动调节网格大小，并快速生成CFD 求解器所需要的高质量笛卡尔六面体网格[5]。最终，齿轮泵内部流场计算流体域网格划分结果如图4 所示，最终的网格数量为616 151 个。

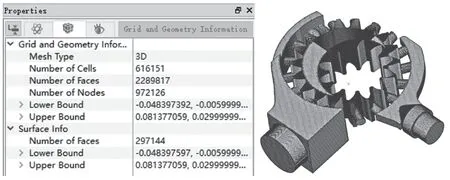
图4 齿轮泵网格划分结果Fig.4 Grid division results of gear pump

由于转子区域、径向通孔区域以及进出油区域的网格是单独划分的，相连的网格之间并不具有传输功能，因此需要创建相应的交互面[6]，包括：补充月牙板区域与月牙板内外侧的交互面、径向通孔外侧与进出油区域的交互面，径向通孔与外齿轮的交互面共3 处交互面，如图5 所示。

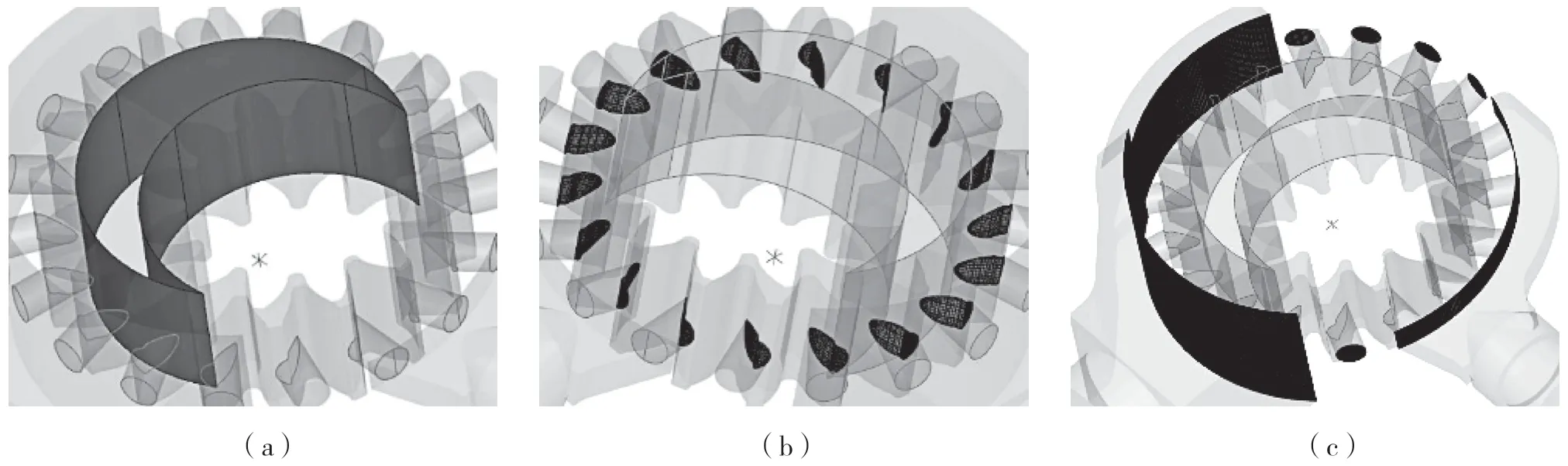
图5 流体域交互面设置Fig.5 Fluid field interaction surface settings

4 设置边界条件和求解参数

将内齿轮的收缩率设为0.1%，外齿轮的膨胀率设为0.1%。此处将齿轮转子旋转周数设为5 圈，旋转轴为Y轴，旋转方向为顺时针，转速为定值1 500 r/min，如图6 所示。

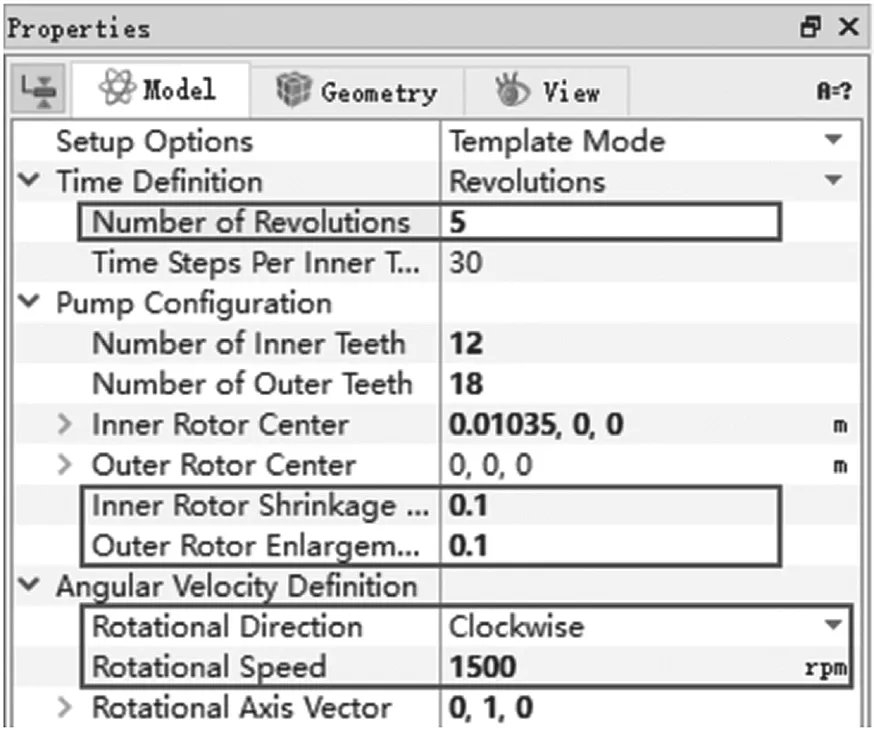
图6 转子求解参数设置Fig.6 Parameter setting of rotor solution

模型设置选择湍流模型，对于齿轮泵仿真用的液压油，为提高齿轮泵内泄露理论模型的准确率，选用的液压油对应参数密度为8 003 kg/m3，动力粘度为0.007 Pa.s，设置结果如图7 所示。

图7 液压油参数设置Fig.7 Hydraulic oil parameter setting

基本计算参数设置完成，最后进行迭代计算设置，如图8 所示。

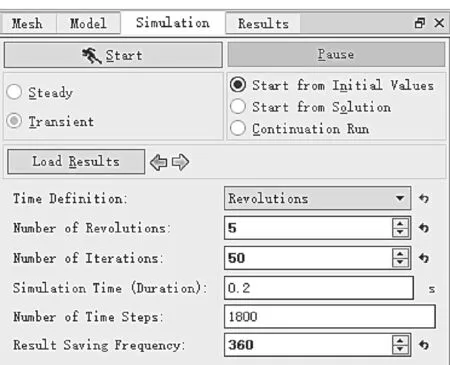
图8 迭代计算设置Fig.8 Iterative calculation setup

5 齿轮泵内流场仿真结果分析

图9 所示为内啮合齿轮泵的负载压强为5 MPa、转速为1 500 r/min、中心距为10.5 mm、内转子收缩率0.1%、外转子膨胀率0.1%的压力云图俯视图，由图9 可直观地观察压力分布情况。

由图9 可见，月牙板将整个流体域分为高压区和低压区两部分，压力从进油口至出油口不断增大，每个齿轮和径向通孔形成的封闭区域压力基本保持不变[7]。同时，在计算区域内，最大压力除出油口在内的整个高压区域外，仅出现在外齿轮和内齿轮的刚啮合处高压区，如图10所示。由图10 可见啮合间隙处呈现的压力变化，最大压力为 6.213 25 MPa，高于设定的额定压力5 MPa，最小压力为1 651.1 Pa。此外，相对其他内啮合齿轮副，有径向通孔的内啮合齿轮副并没有出现负压力。

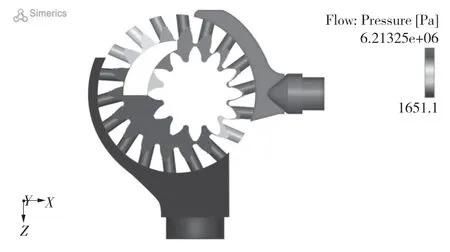
图9 齿轮泵压力云图俯视图Fig.9 Top view of pressure nephogram of gear pump

图10 齿轮啮合处压力分布细节Fig.10 Details of pressure distribution at gear mesh

6 负载对内部流场的影响

分析齿轮泵在不同负载下内部流场的变化。当齿轮泵的转速为 1 500 r/min，负载分别为5，10，15，20，25 MPa 时进行内部流场仿真，分析齿轮泵不同的载荷对其内部流体场压力波动和流量波动的影响。图11 所示为齿轮泵在1 个旋转周期内负载对内部流场最大压力的影响。随着齿轮副的旋转，其最大压力也产生相应波动，且均在0.7 个周期下，在齿轮啮合区域处达到最小值。

图11 不同负载下的压力波动Fig.11 Pressure fluctuation under different loads

从图11 可以看出，齿轮泵的压力波动先降低，在0.7 个周期后显著升高，波动在 20 MPa 时最为明显。负载分别为5，10，15，20，25 MPa 时，最大压力分别达到7.336，12.643，18.184，23.985，28.674 MPa，分别为工作压力的1.47 倍、1.26 倍、1.21 倍、1.19 倍、1.15 倍，逐渐趋向于稳定。

7 结语

相比其它存在困油现象的齿轮泵，最大压力可达工作压力的几倍以上，而该PGH 型内啮合齿轮泵由于在内齿圈齿根处开有径向通孔，在理论上消除了困油现象[8]，使得其受到的压力波动相对更小，从而降低了噪声和振动。