基于时空聚类挖掘的库岸边坡位移监测数据约简

陈 波 ，詹明强 ，黄梓莘

(1. 河海大学 水利水电学院, 江苏 南京 210098； 2. 河海大学 水文水资源与水利工程科学国家重点实验室, 江苏南京 210098； 3. 中国电建集团中南勘测设计研究院有限公司, 湖南 长沙 410014)

库岸边坡的运行稳定对水利工程的服役安全至关重要，其失稳灾害会对工程自身效益和周边安全造成巨大损失。研究表明，库岸边坡失稳破坏会经历渐变到突变的累进发展过程，而边坡运行监测资料记录了失稳灾害孕育的全过程信息，尤其是失稳破坏发生的前兆信息，有必要结合监测资料开展库岸边坡的安全监控和灾变预警研究。

库岸边坡运行的影响因素众多且内在关系复杂，考虑到传统边坡监测分析方法在应对时空数据结构时存在的局限性，有学者引入数据挖掘领域的聚类分析算法，针对边坡工程监测数据的类聚性提取特征和获得知识，为边坡防护治理和科学决策提供依据。如王述虹等[1]将人工鱼群算法和K-means算法相结合，提出一种用于岩体结构面产状分类的改进AFSA-RSK算法，显著提升了运算速度和预测精度；秦雨樵等[2]综合考虑边坡点位移及其对应的点安全系数，提出一种基于K-means聚类算法的滑面搜索方法，有效识别了边坡潜在的危险区域；李佳伟等[3]在考虑边坡稳定性关键影响因素的基础上建立了投影寻踪聚类模型，并进一步结合安全系数法综合评价边坡的稳定性；徐哲等[4]融合K-means聚类及神经网络算法，构建了边坡的稳定性评价模型，并结合工程实例证明所建立模型的预测精确度；王俊杰等[5]采用K-means算法对优势结构面的赤平投影交线进行划分聚类，分类结果较为合理可靠；王卓等[6]结合统计分类和K-means聚类方法对研究区裂缝段进行了危险性分级，为区域的防灾减灾工作提供有力支持；Wang等[7]结合K-means聚类算法、Alpha形状、三次样条插值提出一种自动识别临界滑动面的方法，根据极限状态下的测点位移准确识别边坡二维和三维临界滑动面；金永强等[8]针对边坡运行监测数据的高维非线性特征，采用投影寻踪及和声搜索相结合的算法实现了边坡稳定性的有效评价；Dyson等[9]采用随机有限元法构建边坡稳定性分析模型，针对随机场相似性采用层次聚类分析方法对边坡几何性状进行分类。

综上可见，虽然聚类分析的引入推进了边坡监测数据挖掘的发展，但目前针对动态多方位的实时监测数据的挖掘工作开展较少，挖掘工作的开展深度及挖掘结果的应用频度尚处于浅尝辄止的阶段。基于此，针对边坡监测数据的多维时空特征引入适用于边坡海量监测信息的时空数据挖掘方法，采用K-means聚类算法划分测点区域和投影聚类算法提取数据特征，实现边坡监测数据约简的目的，将深层次的挖掘方法和有价值的挖掘信息应用于边坡安全监测。

1 基于时空聚类分析的库岸边坡监测数据挖掘

边坡监测项目繁多，测点监测信息丰富，采用单项目或单测点的信息评价边坡稳定具有片面性。在时空数据挖掘理论中，聚类分析是将数据集合按照一定规则划分成不同类簇的方法，使划分结果具有“高内聚，低耦合”的显著特征，以达到类内数据相似度高、类间数据相似度低的目的。基于上述聚类思想，根据实际需求的不同又衍生了包括划分聚类、层次聚类、网格聚类、密度聚类和投影聚类等多种算法。

为最大程度挖掘边坡监测资料、反映数据时空特征，本文主要采用划分聚类和投影聚类算法开展时空数据挖掘，分别对边坡监测资料进行测点区域划分和特征提取，以达到边坡监测数据约简的目的。

1.1 基于划分聚类算法的边坡测点分区

K-means算法是一种基于划分的无监督学习的经典聚类算法，通过穷举的方式寻找全局最优结果，并通过计算簇中对象的平均值实现划分目的[10]。算法步骤为：初始化类簇中心、初步划分数据集合、重生成类簇中心、算法收敛判断。重复第2～4步不断更新类簇中心，直至类簇中心不再发生变化时，循环结束并输出聚类结果。

考虑到划分聚类的K-means算法简单易行、效果良好的特点，选取K-means算法进行边坡测点分区。利用K-means算法实现边坡测点分区目的，关键在于灵活构建测点的距离度量指标，综合考虑不同测点之间的相似程度。其中，空间距离指标可衡量不同测点之间空间位置的远近程度，属性距离指标可衡量不同测点之间的属性差异程度。同时，边坡的变形与其稳定性密切相关，变形作为边坡内部稳定状态动态演化的外部直接反映，可以捕捉到与边坡稳定密切相关的物理信息。因此，采用边坡位移测值计算属性距离，同时采用测点水平向和垂直向的空间坐标计算空间距离，不同的距离指标计算式如下：

式中：d1为 测点的属性距离指标；Zi j为 第i测 点第j时刻的位移测值；n为测点总数；m为最长时刻数；Zkj为第k测点第j时刻的位移测值；d2为 测点的空间距离指标；Xi、Yi、Hi表征i测点水平向和垂直向的空间坐标；Xk、Yk、Zk表征k测点水平向和垂直向的空间坐标。

综合考虑属性距离和空间距离，加权确定测点的综合距离指标：

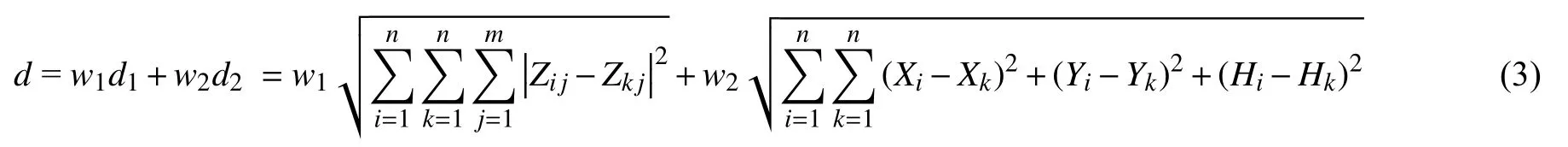
式中：d为测点的综合距离指标；w1和w2分别为属性距离和空间距离指标所占的权重，满足w1+w2=1，通常取w1=w2=1/2。

在构造测点综合距离指标的基础上，基于K-means算法原理实现边坡位移测点的区域划分。

1.2 基于投影聚类算法的边坡位移特征提取

1.2.1 投影聚类算法原理投影聚类是处理高维、非线性及非正态数据的一类新型统计方法，通过寻找反映原始资料数据特征的投影，将高维样本数据映射到低维子空间中[3,11]。基于前面K-means聚类算法的测点分区结果，采用投影聚类算法进一步提取位移数据特征并压缩数据量级。以下分步骤介绍投影聚类算法。

（1）数据无量纲处理。对测点数为n、时序长度为m的边坡位移监测数据集进行无量纲处理，尽可能消除输入数据之间的量纲差异，并将处理后输入数据以x(i,j)表 示，其中，i=1,2,···,n，j=1,2,···,m，x(i,j)为第i测 点的第j时刻值。

为充分提取边坡位移监测数据集的特征，通过采取年均值和年极值两个统计特征对数据集进行描述，以表征数据集的数值大小、极值分布和测值变化等情况。将边坡监测数据集转化为均值集和极值集后再进行无量纲处理，方便后续运算。

（2）构造投影函数。为实现线性空间高维数据的投影，需要构造投影函数，其中，m维 数据的投影方向为则为投影方向上的投影聚类序列值，存在：

（3）构建投影指标函数。投影指标函数有助于最优投影方向的选取，也是将高维数据向低维空间映射的关键。定义投影指标函数为：

式 中：投 影 点zi的 标 准 差Ez为 投影点zi的 平均值；投影点zi的 局部密度rij为样本间距，R为局部数据空间密度的窗口半径，为单位阶跃函数，当R≥rij时，其值为0，反之其值为1。

（4）优化投影指标函数。投影方向a决定了投影指标函数值Q(a)的大小，因此，最优投影方向的选取可以转化为投影指标函数极大值求解的问题，数学表达式为：

（5）综合聚类分析。将步骤（4）求解得到的最优投影方向a*代 入式（4），得到投影特征结果z*(i)。

1.2.2 基于改进投影聚类算法的边坡特征提取投影聚类的关键在于最优投影方向的选取。然而，最优投影方向的求解本身是一个复杂的非线性优化问题，同时由于边坡监测数据量级较大，客观上限制了方法的实用性，有必要引入合适的优化算法帮助确定最优投影方向。因此，引入遗传算法[12]优化投影聚类的计算过程。遗传算法需要确定目标函数，算法目标函数见式（7），约束函数为

适应度函数是评价种群个体好坏的重要因素，要求算法结构简单且计算结果非负，以尽可能降低算法复杂度。根据目标函数设置适应度函数f=Q(a)，由此计算出每个种群个体的适应度值。

2 工程实例

选取某拱坝库首左岸边坡为研究对象。此边坡属于该拱坝的近岸坝坡，距离大坝600～1 300 m，顺河方向长700 m，相对坡高500～700 m。高程1 400 m以上平均坡度为25°～45°，高程1 400 m以下为22°～25°，并有多级缓坡地段。坡面走向约S60°E，岩层产状近EW/S∠30°～35°，边坡为二元结构的单斜顺向坡。由于边坡沿河各段的稳定程度不一，因此在初步设计时，根据边坡地质构造和失稳破坏模式的不同，将1 400 m高程以下的边坡自上游向下游分为Ⅰ、Ⅱ、Ⅲ区，如图1所示。

图1 边坡地理位置示意Fig. 1 Schematic diagram of slope geographical position

2.1 边坡变形区域划分

基于Ⅰ区、Ⅱ区和Ⅲ区共24个地表位移测点的监测数据，包括顺河向、顺坡向和垂直向3个方向，采用Matlab自编K-means聚类算法进行测点区域划分。

在进行划分聚类之前，首先计算测点空间距离和属性距离获得测点的综合距离指标。根据X、Y坐标和高程计算各个测点之间的空间距离，同时，根据顺河向、顺坡向和垂直向的三向位移测值计算各测点的属性距离。在对属性距离和空间距离进行标准化处理后，加权计算获得测点的综合距离指标。

分区结果的正确率为聚类分区结果和勘测设计人员的参考分区结果相吻合的测点数与库岸边坡位移测点总数的比值。

设置初始聚类数目为3，在不指定聚类中心的情况下，计算不同测点间的平方欧式距离以度量测点间的相似程度，并采用循环迭代的方式实现测点区域划分的最优效果。如图2所示，对比基于划分聚类算法的测点分区结果和基于初设资料的测点原始分区结果，在24个位移测点中，除测点交5和交23外，其余22个测点的分区结果均与基于初设资料的测点分区结果吻合，分区正确率达91.7%，这表明基于K-means算法的测点分区结果较为真实可信。

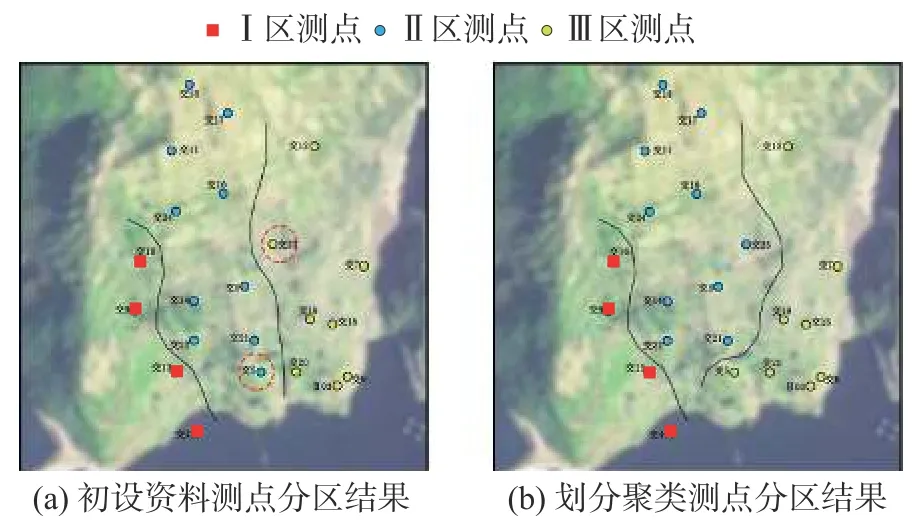
图2 测点分区结果对比Fig. 2 Comparison of zoning results of measuring points

2.2 数据特征提取

在测点分区的基础上，采用遗传算法改进的投影聚类算法，对边坡监测信息做进一步的数据特征提取。首先针对24个地表位移测点1997—2019年的测值，求取三向位移的年均值和年极值，初步提取边坡监测数据集的数据特征，形成6个n=23、m=24的位移测值矩阵在对测值数据进行标准化的基础上，设置遗传算法的运行参数，包括：迭代次数k=50、窗口半径系数α=0.1、变量下界LB=-1、变量上界UB=1。根据投影聚类算法原理，进一步设置相应目标函数、适应度函数及约束函数。

以顺坡区位移年均值为例，经遗传算法的迭代计算，求解获得最优投影方向Ba= （-0.188, 0.324, -0.258,0.066, -0.206, -0.222, 0.140, 0.275, -0.105, -0.114, 0.165, 0.167, 0.400, 0.501, -0.025, 0.275, 0.229, 0.008,-0.039, -0.170, -0.129, 0.040, 0.185）；由此得到顺坡区位移年均值的投影聚类结果：Q(a)=(0.463, 0.468,0.359, 0.237, 0, 0.479, 0.394, 0.352, 0.330, 0.332, 0.172, 0.274, 0.172, 0.052, 0.040, 0.893, 0.301, 0.322, 0.371,0.201, 0.525, 0.037, 0.530, 1.000)，Q(a)各列数值对应各个地表位移测点的投影聚类特征值。同理可得其余方向位移测点年均值、年极值的最优投影方向，以及相应的测点投影聚类特征结果。

综上，各区基于改进的投影聚类算法计算过程如图3、4所示，投影聚类特征值汇总如表1所示。为方便直观对比分析，将表1的投影聚类结果分区域、分方向整理成如图5所示的散点图。根据图5基于遗传算法的位移测点投影聚类结果，以投影聚类特征值作为判断指标，可以筛选出需要重点关注的测点。

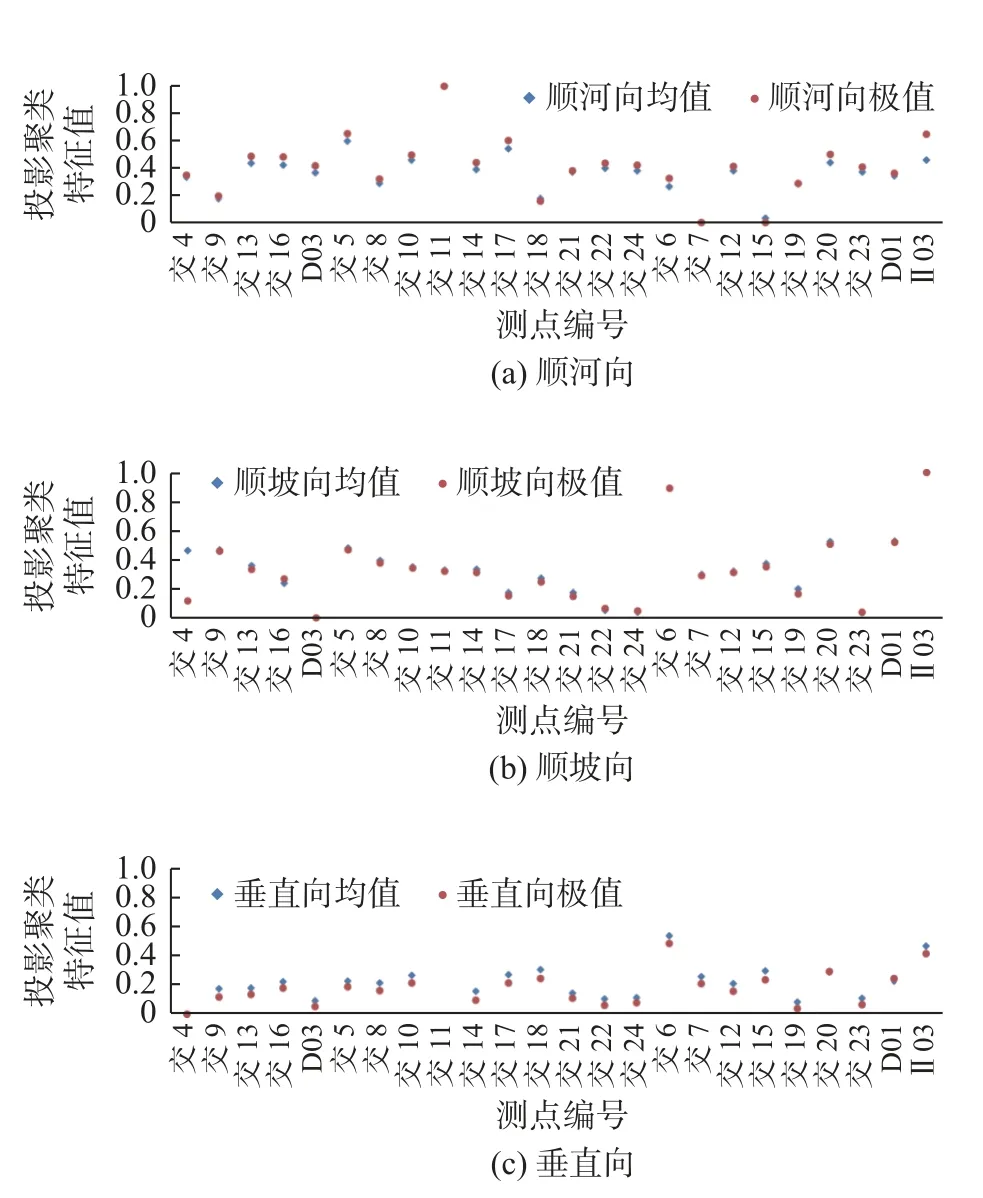
图5 基于遗传算法的位移测点投影聚类结果Fig. 5 Projection clustering results of displacement measuring points based on genetic algorithm

表1 基于遗传算法的分区位移测点投影聚类结果Tab. 1 Projection clustering results of subarea displacement measurement points based on genetic algorithm

图3 遗传算法改进的投影聚类计算过程（均值）Fig. 3 Improved projection clustering calculation process diagram of genetic algorithm (mean value)

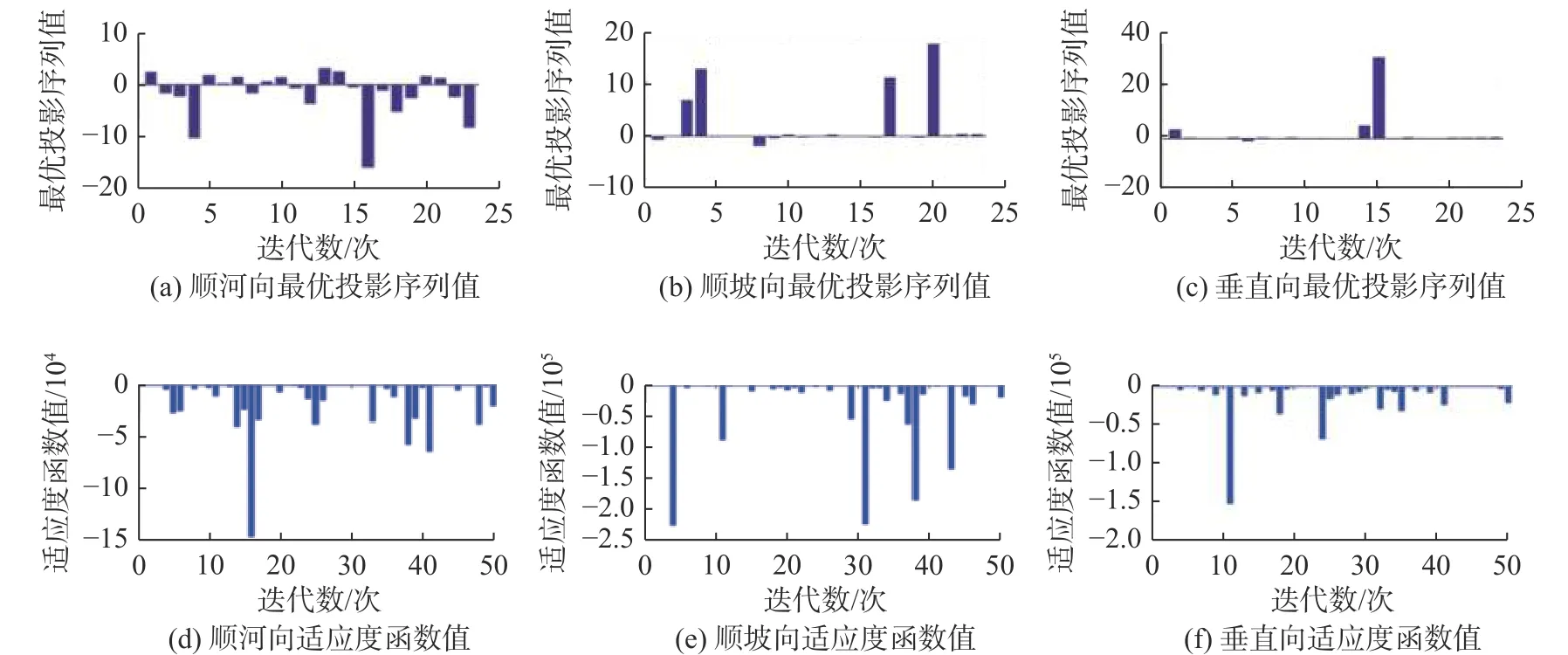
图4 遗传算法改进的投影聚类计算过程（极值）Fig. 4 Improved projection clustering calculation process diagram of genetic algorithm (extreme value)

以顺河向位移测值的投影聚类计算结果为例，结合图6（a）所示的典型测点的测值过程线，可以看出：年均值和年极值投影聚类特征值最大的都是测点交11，最小的都是测点交7，分别对应顺河向测值序列中的极大值和极小值，两个测点的位移时间曲线各自向正负两个方向延伸，而投影聚类特征值趋近于中值水平的测点，如测点交10，测值波动幅度不大且不存在明显递增、递减趋势，测点运行状态比较安全。

图6 典型测点位移过程Fig. 6 Typical displacement process of measuring points

根据上述规律筛选出其余两个方向需要重点关注的测点。在顺坡向测点中，大部分测点的投影聚类特征值均小于0.6，测值变化比较平稳，而投影特征值趋近于1的Ⅲ区测点Ⅱ03和交6都呈现出明显递增趋势，20年间的测值变幅达到600 mm；在垂直向测点中，除Ⅱ区的测点交11外，其余测点的特征值均小于0.6，测值变化规律相似且发展态势平稳。

由上述分析可见，基于遗传算法优化的投影聚类算法可以有效提高计算效率、压缩数据量级，同时根据计算结果能快速提取测点数据特征，直观反映出不同区域、不同方向的测值分布情况，筛选出其中需要重点关注的测点。

3 结 语

结合工程实际，针对边坡监测信息的多维特性和时空特征，引入时空数据挖掘领域的聚类方法，开展多测点多项目海量边坡监测信息的时空数据挖掘工作。结果表明， 综合考虑库岸边坡测点属性特征和空间特征，采用K-means算法度量测点间的相似程度，可实现测点区域准确划分。在测点分区的基础上采用遗传算法优化的投影聚类算法，将高维数据向低维空间进行映射，可以提取测点数据特征，从而压缩数据量级并筛选出需重点关注的测点，即基于聚类分析逐步实现了边坡位移监测数据的约简。