基于隐马尔可夫模型动作模仿建模研究

沈睿婷，张 雷

（北京建筑大学 电气与信息工程学院，北京 100044）

0 引言

模仿学习（Imitation learning）旨在模仿给定任务中的人类行为。通过学习观察和行动之间的映射，对代理（学习机器）进行训练，以从演示中执行任务[1]。随着智慧城市，人机共居等概念的出现，仿人机器人的模仿学习成为了研究热点。

仿人机器人对于人体动作的模仿学习过程主要可以分为以下三个阶段：

1）观察和记录人体的运动，获取人体运动数据；

2）将采集到的人体运动数据转换为便于仿人机器人进行动作模仿的数据格式；

3）最后仿人机器人根据观察到的动作数据进行动作模仿。

模仿学习在机器人领域很多应用。Kim等人[2]提出了一种仿人机器人运动生成方法，使用运动捕捉系统获得的数据，提出一种优化策略来解决逆运动学问题。Gams等[3,4]提出一种基于RGB-D相机捕获的人体运动数据进行在线运动模仿的方法。Koenemann等人[5]提出一个仿人机器人实时模仿人体复杂全身运动的系统。Inamura等[6]提出使用隐马尔可夫模型（HMM）对人类运动原语进行建模。Ijspeert等人[7～9]提出使用动态运动基元（DMPs）对人体运动建模的方法。Mina等人[10]提出了一种基于实时反运动学的实时人体仿真系统，将人体上肢运动安全平滑地映射到机器人的关节上。Garam[11]等人提出了一个包含基于主成分分析(PCA)的进化过程的模仿学习框架。

针对仿人机器人对人体动作的模仿已经开展了大量研究，并且积累了一些研究成果，但这些研究采用的方法大多数都是离线地、一次性地对人体动作进行采集和学习，不能实现在仿人机器人持续动作观察和学习。为实现仿人机器人的连续模仿学习，本文提出了仿人机器人动作模仿框架如图1所示。

图1 仿人机器人动作模仿框架

1）将观察到的人体动作骨骼点位置数据转换成方便仿人机器人计算的关节角度序列，并计算得到角速度序列和角加速度序列，组成完整的人体动作数据，以供仿人机器人模仿学习。

2）应用高斯混合隐马尔可夫模型（Gaussian-HMM）对动作数据进行建模，生成动作模型。

3）仿人机器人可以通过对已训练的模型进行学习，生成适合机器人自身的动作。同时训练完成的模型还可以对新出现的动作进行判断，判断新动作是否已学习的动作。利用此框架可以实现仿人机器人对人体动作在线连续地学习。

动作模型建模是仿人机器人动作模仿框架中较为重要地部分，以此为基础可以进行动作生成，故本文主要对人体动作数据匹配与动作模型建模方法进行介绍。本文具体结构如下：首先，在第2节对仿人机器人和人体动作数据进行匹配计算，在第3节介绍基于HMM的建模与识别的方法，第4节将介绍相关实验结果。

1 人体动作数据匹配计算

建模之前需要将采集到的人体运动数据转换为便于仿人机器人进行动作模仿的数据格式，需要将坐标点转换成为仿人机器人相关关节角度，角速度和角加速度等，这个过程就是人体动作数据匹配计算的过程。

本文将用MSR Action3D数据集来进行与NAO机器人的人体数据的匹配计算，MSR Action3D数据集是一个由深度相机捕获人体动作的深度图像序列数据集[12]该数据集共包含高挥手臂、画“√”、网球发球等20种动作类型，如图2所示。

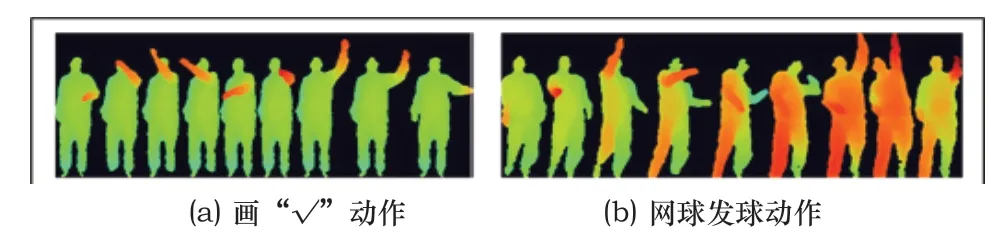
图2 MSR-Action数据集中的动作

MSR Action3D数据集中包含了人体20个骨骼点在笛卡尔坐标系下的坐标和置信度。人体骨骼点对应如图3所示，图中坐标轴分别代表笛卡尔空间坐标系下的X、Y、Z轴。

本文利用骨骼点坐标信息得到对应的关节向量，再利用计算关节向量的夹角得到对应的关节角度。图3中标号相对应的关节点以及关节的自由度相对应的关节点信息如表1所示。

表1 各关节自由度对应关节点信息

图3 人体骨骼点位置

以左肩部的翻滚角（LShoulderRoll）为例。肩部的翻滚角（LShoulderRoll）可以用肩部（ShoulderL）和手肘（ElbowL）形成的关节向量与肩部和肩部中点（ShoulderCenter）形成的关节向量的夹角求出，分别用p1，p8，p3，具体位置如图4所示。

LShoulderRoll是根据坐标系绕Z轴左右旋转得到的角度（坐标系的建立如图4所示），p1p′8和p1p′8′为两个左臂可能旋转到的位置，所以LShoulderRoll的自由度的旋转角度相当于求解p1p8与p1p′8或p1p8与p1p′8′之间的夹角。为了的到这个夹角可以用p1p3与p1p′8或p1p3与p1p′8′之间的夹角减去p1p8与p1p3之间的夹角得到。由于NAO机器人的手臂初始位置是水平的（图4），所以p1p8与p1p3之间的夹角为90°。再根据绕旋转轴的方向，逆时针方向旋转为正，顺时针方向旋转为负，添加正负号校正旋转角度。

图4 NAO机器人初始位置及左臂翻滚角示意图

综上，左手臂肩部翻滚角（LShoulderRoll）可以定义为：

同理可得右手臂肩部翻滚角（RShoulderRoll）可以定义为：

此处p2，p3，p9分别表示骨骼点ShoulderR,Shoulder-Center,ElbowR。

剩下的关节角度都与ShoulderRoll的计算类似，可以根据选取向量的方向，取正负或者π的倍数来校正。

因为机器人机械结构的限制，各个自由度的旋转角度需要满足机器人关节角度约束。所以根据NAO机器人（如表2所示）的关节角度约束，对上述方法匹配计算的的旋转角度进行处理优化。

表2 各关节自由度对应关节角度约束

经过旋转角度的数据优化处理，可以规避一些不合理的动作。如图5所示，图5为旋转角度优化处理前后对比图，上图为优化处理前数据图像，下图为优化处理后，数据优化处理去除了一些较为极端的角度。

图5 旋转角度优化处理前后对比图

通过以上方法就能得到全身各个自由度的旋转角度。将观察到的人体动作过程中关节位置的变化数据，转化为关节角度随时间变化的序列数据，根据角度变化序列计算出角速度变化序列和角加速度变化序列。

由于动作序列采集过程中，每一帧的时间间隔非常短，因此将角速度的计算公式定义为：

其中，st为所求的角速度，T为角度序列的长度，θt为t时刻的关节角度。根据角速度，可以求得角加速度At为：

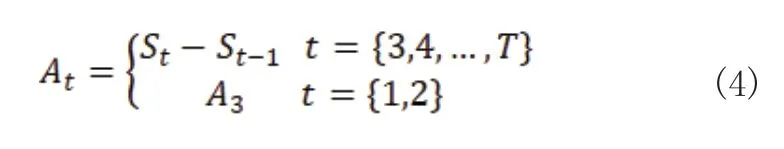
并将这些序列数据组合成为动作数据。然后，应用高斯隐马尔可夫模型对动作数据进行建模，生成动作模型。

2 基于HMM的动作建模、识别

隐马尔可夫模型（Hidden Markov Model，HMM）是一种随机概率模型，在上个世纪六十年代后期由Leonard等人提出，并在七十年代中期开始用于语音识别[13]。

HMM模型（图6）包含五个重要的概念：观测序列集合s={o1，...，oM}；隐藏状态集合Q={q1，...，qN}；隐藏状态初始概率分布π={πi}1；状态转移概率矩阵A={aij}，aij表示从第i个状态转移到第j个状态的概率；以及输出概率矩阵B={bij}，其中，bij表示第i个状态输出第j个标签的概率。可以将一个HMM模型λ定义为：λ={A，B，π}。本文中人体动作数据是观察序列S，将人体动作数据按照状态数分为一小段的动作数据是隐藏状态Q。

图6 HMM模型

隐马尔可夫模型根据离散的输出和连续的输出可以分为离散隐马尔可夫模型（DHMM）和连续隐马尔可夫模型（CHMM），如图7所示。因动作输出是随时间变化连续的输出，故本文利用高斯隐马尔可夫模型（Gaussian-HMM）进行建模。假设输出概率密度函数符合高斯分布，则输出概率为：

图7 连续隐马尔可夫模型

若输出概率密度函数符合高斯混合模型分布，则输出概率为：

2.1 基于HMM的动作建模

动作建模的过程相当于求解模型参数。已知观测序列求解调整模型参数，即已知观测序列，求解模型的参数（隐藏状态初始概率分布Π，状态转移矩阵A，输出概率矩阵B），使得此情况下观测序列概率最大，使用基于EM算法的鲍姆-韦尔奇算法（Baum-Welch algorithm）可以求解HMM的模型参数，相当于完成建模的过程。

鲍姆-韦尔奇算法（Baum-Welch algorithm）[14]是EM算法（也称为前向-后向算法）的变形和延伸，可以用来估计HMM的模型参数。在HMM中，为了使关联算法易于处理，对观测序列S和隐藏状态Q这些随机变量有两个条件独立性假设：1）第i个状态只与第i-1个状态有关，与之前的状态无关；2）第i个观测只与第i个状态有关，与其他变量无关。

鲍姆-韦尔奇算法将分为两步估计模型参数。

E Step：

（1）递归方法计算前向概率（Forward Probability)ai(t)和后向概率（Backward Probability)βi(t)。

（2）计算状态占有概率（State Occupation Probability）γi(t)和γij(t)。

M Step：根据状态占有概率重新计算HMM模型参数。

重复进行以上两个步骤，直到算法收敛，得到估计的HMM模型参数。具体计算流程如图8所示。

图8 鲍姆-韦尔奇算法计算流程

利用鲍姆-韦尔奇算法对第2节得到的动作数据进行建模得到HMM模型参数如图9所示，分别包括了隐藏状态初始概率分布、状态转移概率矩阵以及输出概率密度函数的均值与方差。

图9 计算得到HMM模型参数

2.2 基于HMM的动作识别

通过以上方法可以对不同的动作数据进行建模，为验证建模的有效性，判断新观察到的动作属于哪类已经建模的动作，这些属于动作识别问题。为了对新观察到的动作进行识别，首先需要将新观察到的运动转换为可被建模的动作数据O，然后求出每个已建立的动作模型生成该动作序列的似然值P(O丨Mi)，其中Mi是已建立的动作模型，Mi∈{M1,M2,M3,...,Mn}，P(O丨Mi)的值可由上一节中提到的鲍姆-韦尔奇算法计算得到。则通过判断似然值P(O丨Mi)的大小可以得到识别结果，新观察到的动作属于似然值P(O丨Mi)最大的动作模型。

当动作数据维度增加时，动作识别结果的似然值会降低，导致动作识别失败，改变隐藏状态的个数的数值可以提高动作识别结果。当似然值P(O丨Mi)中最大的值与第二大的值相差越大，则动作识别结果越好。可以引入以下准则：

其中，max{P(O丨Mj)}表示在已经建立的动作模型中，对观察到动作序列的最大似然值，second{P(O丨Mk)}表示对观察到动作序列的第二大似然值。则R的绝对值越大，表明似然值P(O丨Mi)中最大的值与第二大的值相差越大，则动作识别结果越好。可利用R的值，对不同状态数下得出的模型识别效果进行比较，得到最优的状态数。

3 实验

实验分为了三个部分，验证向量方法计算关节自由度旋转角度的正确性实验，验证基于Gaussian-HMM模型的动作建模和动作识别方法的有效性实验以及HMM模型状态数对动作模型识别结果影响实验。

3.1 验证向量方法计算关节自由度旋转角度的正确性实验

为了验证向量方法计算关节自由度旋转角度的正确性，利用NAO机器人的仿真平台输入计算得出的旋转角度与原数据集进行比较得到（如图10所示）：可以发现同一时刻，仿真得到的图像与原数据集动作基本一致，从而验证本文所提出的向量计算得到的旋转角度是正确的。

图10 向量方法计算旋转角度正确性验证

3.2 验证基于GAUSSIAN-HMM模型的动作建模和动作识别方法的有效性实验

为了验证基于Gaussian-HMM模型的动作建模和动作识别方法的有效性，选取MSR Action3D数据集中的数据集较为完整精确的动作1（高挥右臂）、动作2（水平挥右臂）、动作6（右臂高抛动作）、动作7（右臂画“×”）、动作8（右臂画“√”），这5个动作进行动作识别实验。在每个动作的多条序列中，随机选取3个序列组成测试集，其余序列组成训练集。

首先用Gaussian-HMM模型对5个动作的训练集中右臂的动作数据进行建模。建模完成后用测试集进行动作识别，测试集包括了5个动作数据集中随机的一个序列。计算测试集中的动作序列与已建立的模型的似然值，通过似然值的比较得出动作识别的结果，如表3所示，M1-M5代表五个训练完成的模型，a1-a5代表测试集中的五个动作数据，max代表计算测试集中的动作序列与已建立的模型的似然值最大的模型。

表3 动作识别实验结果

似然值越高说明序列与模型越匹配，从实验结果可以看到，对于每条动作序列，与其匹配的模型生成该序列的似然值最高。对于每个已经建立的模型，生成与其匹配的那条序列的似然值最高。5条动作序列和建立的5个模型可以成功实现互相识别，实验结果验证了动作建模和识别方法的有效性。

3.3 HMM模型状态数对动作模型识别结果影响实验

增加动作数据，用Gaussian-HMM模型对5个动作的训练集中左右臂的动作数据进行建模，计算测试集中的动作序列与已建立的模型的似然值，结果如表4所示，M1-M5代表五个训练完成的模型，a1-a5代表测试集中的五个动作数据，max代表计算测试集中的动作序列与已建立的模型的似然值最大的模型。

表4 增加动作数据后模型动作识别实验结果

由表4可得增加动作数据，而不改变HMM模型隐藏状态数，动作识别会出现错误。改变状态数，并计算R值，可以得到随着状态数改变，动作识别效果改变情况，如图11所示。

由图11可得，R的绝对值随状态数变大而变大，到达一定值后达到顶点，动作识别效果最好，由此可得出HMM模型最优的状态数。

图11 R值随状态数变化曲线

4 结语

本文通过向量方法求解动作数据，并通过Baum-Welch算法对Gaussian-HMM模型参数进行估计，从而对动作数据建模。再用新观察到的动作序列与已建模的模型的似然值比较，验证基于Gaussian-HMM动作建模和识别方法的有效性。