地铁上盖大底盘多塔层间隔震结构的抗倒塌性能分析

袁涛涛，蔡玉军，李衍赫，王 洋，吴函恒

(1.中铁第一勘察设计院集团有限公司，陕西 西安 710043；2.长安大学 建筑工程学院，陕西 西安 710061)

近年来，随着城市化进程的加快，城镇居民人口比例急剧上升，导致城市可利用空间骤然下降。为了提高城市空间利用率，在地铁上盖部分建设大底盘，然后设置塔楼已经成为一种趋势。采用传统的抗震结构，会增加底部结构的截面尺寸，从而增大下部结构的刚度，同时也会对地铁运营空间产生不利的影响。因此，为了解决刚度突变的问题，将层间隔震技术引入地铁上盖开发的过程中，引起了国内外学者的广泛关注[1～9]。

赵楠等[10]通过增量动力时程分析研究了在多遇和罕遇地震作用下，大底盘多塔高层隔震结构响应，研究结果表明：隔震结构的地震作用显著降低。邓烜等[11]采用理想化质点系模型对大底盘多塔隔震结构进行了分析，提出了大底盘多塔楼设计时应根据各塔楼的特性并采用多种计算模型综合对比的设计方法。周颖等[12]通过对两个上部结构形式不同、体积相当的大底盘单塔建筑进行了振动台试验研究，对比分析了破坏情况、动力特性及响应，并提出此类建筑结构的设计建议。陈云等[13]通过数值分析和振动台试验研究了偏心大底盘层间隔震结构的地震响应，并提出在实际工程中应加强底盘受力构件的建议。

在强震作用下，保证建筑结构的抗倒塌能力，是建筑抗震设计的核心目标。目前结构抗倒塌能力评价最为合理的方法是基于弹塑性时程分析的倒塌易损性分析方法。基于增量动力分析(IDA)方法，国内外研究者对结构的倒塌易损性进行了一系列研究。Vamvatsikos和Cornell[14-15]对增量动力分析方法进一步深度研究和总结。我国学者陆新征等[16]研究了构件层次和整体结构的安全储备系数，并考虑了影响安全储备系数的因素，同时利用基于IDA法的倒塌储备系数对7度设防条件下不同层高框架结构的倒塌能力进行评估。樊剑等[17]研究了不同结构参数对隔震结构工程需求参数的影响，并根据增量动力时程分析结果，绘制了隔震上部结构最大层间位移角和隔震支座最大位移的超越概率曲线。任叶飞等[18]对比了不同地震动输入下的易损性结果，建议采用考虑场址危险一致性与结构自振特性的地震动输入选取方法。

本文对大底盘多塔层间隔震结构建立分析模型，进行增量动力时程分析，建立易损性曲线，根据FEMA P695[19]和《建筑结构抗倒塌规范》[20](CECS 392:2021)对该结构抗倒塌能力进行评估，探讨层间隔震结构的破坏模式，提出使用高阻尼橡胶支座来控制隔震层的变形，并对比研究地震下叠层橡胶支座和高阻尼橡胶支座对结构的影响。

1 工程概况

项目为西安某地铁停车场，受建设条件的需求，设计分为盖上、盖下两个部分。该工程结构设计基准期和使用年限50年，安全等级为二级，结构重要性系数为1.0，抗震设防烈度为8度，0.2g，建筑抗震设防类别为丙类，建筑场地类别为II类，设计地震分组为第二组，特征周期为0.40 s。50年重现期基本风压为0.35 kN/m2，基础设计安全等级为二级，基础设计等级为甲级。主要构件截面尺寸如表1所示。其中隔震支座的属性见表2，塔3的支座布置见图1。

表1 主要构件截面尺寸

表2 隔震支座的规格和力学性能

图1 隔震支座的布置

2 结构分析模型

采用ETABS软件分析计算，整体模型如图2所示，其中隔震支座采用“Rubber Isolater+Gap”单元模拟，梁、柱构件采用框架单元模拟，楼板采用膜单元模拟，下部结构剪力墙采用厚壳单元模拟，而上部结构剪力墙采用薄壳单元来模拟(忽略横向剪切变形)。混凝土本构模型采用武田(Takeda)三线性模型，钢材本构模型采用双线性随动强化模型，如图3所示，根据试验的相关数据确定本构模型的相关参数[21]。弹塑性分析时，框架梁采用只考虑弯矩M3的塑性铰，框架柱采用P-M2-M3纤维铰。采用分层壳单元来模拟下部结构剪力墙的非线性行为，由于上部结构剪力墙高宽比较大，所以采用墙铰(P-M3)来模拟墙体的非线性行为。墙铰模拟墙体的压弯行为，墙体的剪切行为仍是弹性的，取决于材料的剪切模量，压弯和剪切行为没有耦合。

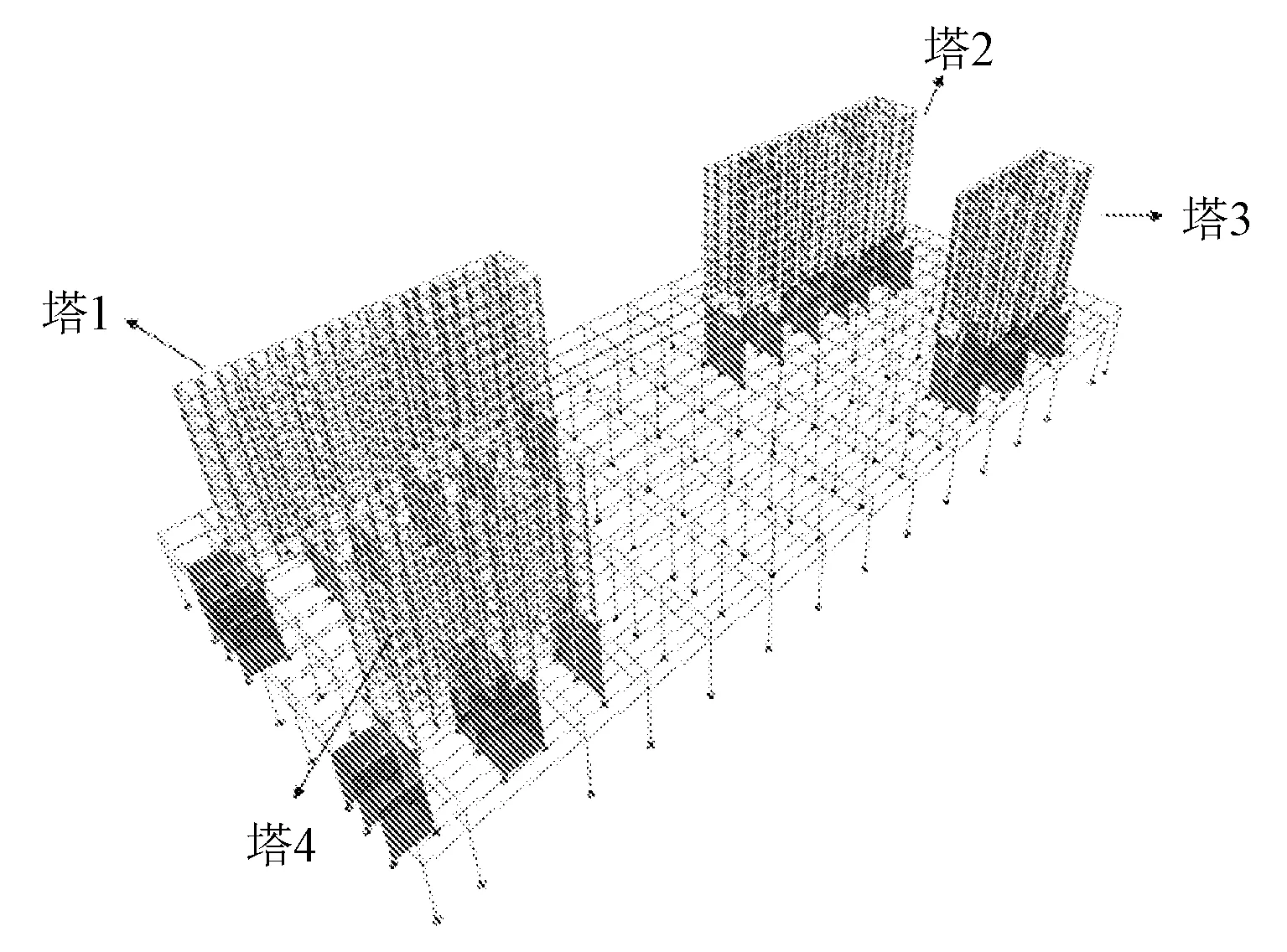
图2 结构分析整体模型

图3 本构模型

3 基于IDA的倒塌易损性分析

3.1 地震动的选择

本文采用FEMA P695[19]推荐的22条远场地震波进行IDA分析。与此同时，将规范谱与所选反应谱进行了对比(见图4)。

图4 对比规范谱与所选地震波反应谱

3.2 IM指标和DM指标的选择

将某条特定的地震动记录按一定比例进行一系列单增的调幅，形成多条地震动记录，这一系列的幅值从小到大排列作为增量动力分析(IDA)的地震动烈度指标(IM)，选取地面峰值加速度(PGA)作为IM指标，本工程为大底盘多塔层间隔震结构，选取三个DM指标，分别为下部结构最大层间位移角，隔震支座位移和上部结构最大层间位移角[22]。本文采取等步长0.20g的方式对地震动进行调幅，起始地震动为0.10g，将每条地震波调幅至1.50g或者DM指标超过倒塌限值。

3.3 结构倒塌判断准则

FEMA 350[23]规定当达到倒塌状态时，初始斜率的20%为IDA曲线的斜率。隔震结构由于隔震层刚度较小，地震作用下易出现大变形，因此本文定义达到倒塌状态时即位移角或者支座位移达到了规范限值。

本工程下部结构是框剪结构，上部为剪力墙结构。《建筑抗震设计规范》[24](GB 50011—2010)和《建筑隔震设计标准》[25](GB/T51408—2021)规定的弹性和弹塑性的位移角限值如表3所示。因此本文结合《抗规》和《隔规》定义下部框架剪力墙结构在罕遇地震下的倒塌限值为1/200，上部结构剪力墙位移角倒塌限值为1/250。极罕遇地震下，上部结构倒塌限值为1/120，下部结构倒塌限值为1/130。罕遇地震下支座位移的倒塌限值为min(0.55支座直径，3倍橡胶总厚度)=440 mm，极罕遇地震下支座的倒塌限值为橡胶层总厚度的4倍[26]，其值为592 mm。

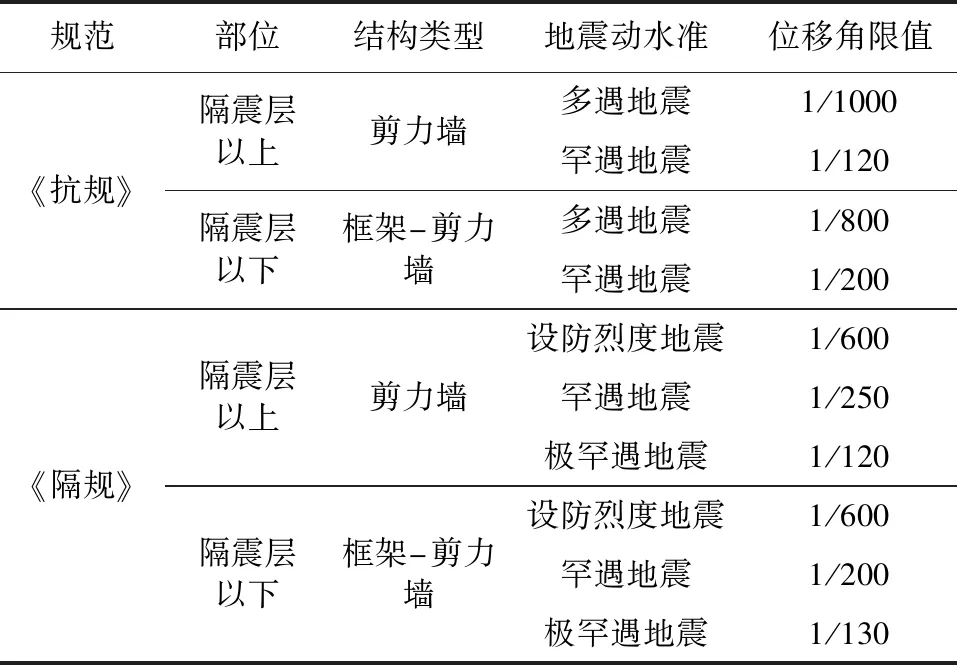
表3 规范对层间位移角的限值

4 分析结果

4.1 易损性曲线

将所有弹塑性分析结果汇总成为IDA曲线如图5，横坐标为DM指标，纵坐标为IM指标。

结构需求参数(EDP)和地震动强度参数(IM)满足关系式：

EDP=α(IM)β

(1)

本文EDP为结构损伤参数θmax和隔震支座位移，地震动强度参数IM为PGA，代入式(1)，两边同时取对数得：

ln(θmax)=a+b·ln(PGA)

(2)

式中：a=lnα，b=β，且a和b的值可通过对增量动力时程分析得到的IDA曲线进行线性回归定义，见图6。

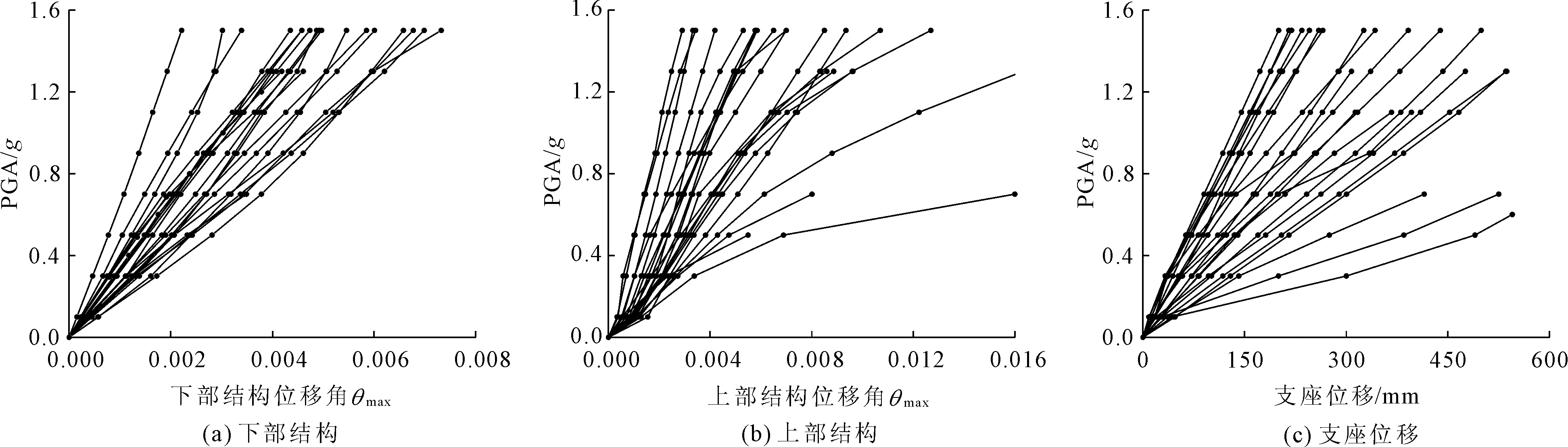
图5 IDA曲线

图6 IDA曲线回归分析

地震易损性曲线描述了结构不同地震动强度作用下，结构地震反应D大于结构定义的抗震能力参数C的条件概率Pf，如式(3)所示：

Pf=P(C-D<0)

(3)

假设D和C均服从对数正态分布，则结构的失效概率可表示为：

(4)

根据上述方法，可以得出结构的概率需求模型表达式，以下部结构层间位移角为例，根据前述拟合结果，可以求出α=0.002 749，β=0.985 81，代入公式(4)可得：

(5)

将不同的地面峰值加速度(PGA)代入公式(5)，根据正态分布表可计算出结构超越或达到某性能状态的概率对应不同的地震动强度，如图7所示。

图7 隔震结构的倒塌易损性曲线

从图7中可以看出支座位移的倒塌概率最大，当在罕遇地震下(0.4g)，支座位移的倒塌概率为2.1%。满足FEMA P695[19]中规定的最大考虑地震(MCE)，对应我国罕遇地震下的可接受倒塌概率为10%。当PGA达到0.60g时，支座位移倒塌概率为7.49%，上部结构倒塌概率为0.94%，下部结构倒塌概率为1.39%。

4.2 基于FEMA P695的抗倒塌性能评估

FEMA P695[7]体系提供了一套完整的抗倒塌评估标准化流程和评价准则：在不同地震强度作用下，对结构进行弹塑性分析(IDA)，得到结构的倒塌概率，将其连线，即得到结构的易损性曲线，并提出结构倒塌储备系数CMR作为评判结构抗倒塌能力指标。结构倒塌储备系数CMR(Collapse Margin Ratio),又称为倒塌富余度，CMR用SCP与SMT的比值来定义，如公式(6)所示。用量化的CMR值来衡量结构抗倒塌性能，CMR值越大，结构倒塌概率越小。

(6)

式中：SCP为结构易损性曲线倒塌概率50%时对应的地震动强度；SMT对应我国规范中罕遇地震下第一周期对应的谱加速度。

根据易损性曲线可知，支座位移的倒塌概率50%对应的地震动强度SCP为1.0g。SMT可以根据规范谱的公式在第一周期3.2 s求出为0.189 8g。因此代入公式(6)得出此大底盘多塔层间隔震结构倒塌储备系数CMR为5.269。

将反应谱形状对结构倒塌储备系数产生的影响纳入考虑范围，利用反应谱形状调整系数(SSFi)，调整结构倒塌储备系数(CMR)，修正后的倒塌储备系数ACMR计算公式为:

ACMR=SSFi×CMR

(7)

式中：SSFi为结构第一自振周期T1、延性系数μc以及设计地震分组的函数，根据FEMA P695[19]，得出SSFi=1.37，可计算ACMR=7.219。

4.3 结构总的倒塌不确定性计算

结构倒塌概率受多种因素的影响，变异性过大会引起结构倒塌储备系数(CMR)过大，由此才能保证较小的结构倒塌概率。结构总的不确定性系数βTOT，计算公式如下：

(8)

式中：βTOT为结构倒塌总的不确定性系数;βRTR为与地震动相关的不确定性系数;βDR为与设计要求相关的不确定性系数;βTD为与试验数据相关的不确定性系数;βMDL为与模型质量相关的不确定性系数。

由于弹塑性模型配筋做了一定简化，并且上部结构剪力墙没有考虑压弯和剪切耦合，因此选择非线性模型质量为一般。

国内外对橡胶支座开展了较多的试验研究和理论研究，因此，数值模型模型的准确性可由已有的试验数据来验证。由于试验数据比较成熟，认定试验数据属于良好范畴，认定设计质量属于良好范畴，依据FEMA P695[19]，得出总的不确定性系数βTOT为0.600。

根据FEMA P695[24]提出的不同βTOT、不同倒塌概率下的可接受倒塌储备系数调整值ACMR，可以得出，当βTOT为0.600时，20%倒塌概率下可接受ACMR值(用于衡量个体结构的抗倒塌能力)为1.66，通过公式(7)计算得出的ACMR值为7.219远大于1.66，满足大震不倒的要求。

4.4 基于CECS392:2014的抗倒塌性能评估

我国《建筑结构抗倒塌设计规范》[20]给出了采用基于IDA的易损性分析法时的可接受倒塌概率，如表5所示，倒塌概率的计算公式为：

(9)

式中：Ncollapse为该强度地震作用下发生倒塌破坏的地震动数。

通过IDA分析计算出的数据可知，在罕遇地震下(0.4g)，支座位移发生倒塌破坏的地震动数有1条，为1244波。因此计算出罕遇地震下的倒塌概率为Pcollapse=1/22=4.5%。极罕遇地震下(0.6g)有2条波，分别为1158波和1244波使支座位移发生倒塌破坏，Pcollapse=2/22=9%。而本工程建筑抗震设防类别为丙类，因此满足规范罕遇地震和极罕遇地震下的可接受倒塌概率。

表4 结构可接受最大地震倒塌概率

5 强震下隔震层位移的控制研究

由前文对大底盘多塔层间隔震结构的抗倒塌性能分析的结论可知，大震下隔震支座位移的倒塌概率最大，可能会导致上部结构整体倾覆，所以要采取相应措施来限制隔震层的位移，但如果只是增大橡胶支座的刚度来减小位移势必会引起隔震效果的降低，所以叠层橡胶支座的刚度和位移就是一对矛盾，如何解决此矛盾是当下研究的热点。

目前我国在天然橡胶支座(LNR)和铅芯橡胶支座(LRB)的应用慢慢得到普及，在各种住宅建筑和公共建筑中已经得到应用。不过这些普通橡胶支座也有明显的缺点，一是在低温环境下橡胶会发生硬化降低隔震性能，二是LRB支座里的铅芯会对环境造成严重的危害。试验研究[26]表明LRB支座在低温条件下容易迅速硬化，大大降低支座的阻尼性能。为了更好的满足隔震结构在强震下的位移控制和保护环境的要求，本文认为新型的高阻尼橡胶支座能更适用于建筑工程减隔震领域。高阻尼隔震橡胶支座(High Damping Rubber Bearing，简称HDRB)是将天然橡胶支座中加入各种添加剂、补强剂、可塑剂、硫化剂来提高橡胶的阻尼性能，然后使用这种大阻尼橡胶和钢板经过热硫化而制成。高阻尼橡胶同时拥有粘性流体特性和弹性固体的特性，其耗能原理是通过橡胶的流体运动产生的热能和弹性变形产生的势能一起去耗散地震能量[15]，这使它吸收地震能量的能力比普通的叠层橡胶支座要强，所以高阻尼橡胶支座不仅能承受较大竖向荷载，而且同时还能抵抗较大的水平剪切位移。

5.1 高阻尼橡胶支座的力学模型

高阻尼橡胶支座滞回环表现饱满，有较大的耗能能力，其滞回曲线如图8所示。该支座在小变形范围内就表现为非线性，在小变形领域，高阻尼橡胶支座刚度较大，刚度随着变形的增大而发生软化，在剪应变达到200%后出现硬化，而且该支座的非线性属性与变形大小、反复次数和位移历程均有关。

图8 高阻尼橡胶支座的滞回模型

在工程中为计算方便，更多的是采用经过简化的等效双线性模型来模拟高阻尼橡胶支座的性能。根据我国规范《公路桥梁高阻尼隔震橡胶支座》[27](JT/T 842—2012)附录A.4.2条，高阻尼橡胶支座可以采用如图9所示的双线性恢复力模型进行分析计算。与普通铅芯橡胶支座(LRB)计算模型[28]相比，高阻尼橡胶支座采用双向性恢复力模型时与铅芯橡胶支座的恢复力模型相同，因此在程序中中同样适用“rubber isolator”单元来模拟高阻尼橡胶支座。然而，高阻尼橡胶支座HDRB比其他橡胶支座具有更强的非线性效应。研究表明[29]，对于HDRB，传统的双线性模型适用于低至中等水平的剪切应变，但无法有效的描述更大的剪切应变，而DHI模型可以较好的模拟高阻尼橡胶支座。

图9 HDRB双线性滞回模型

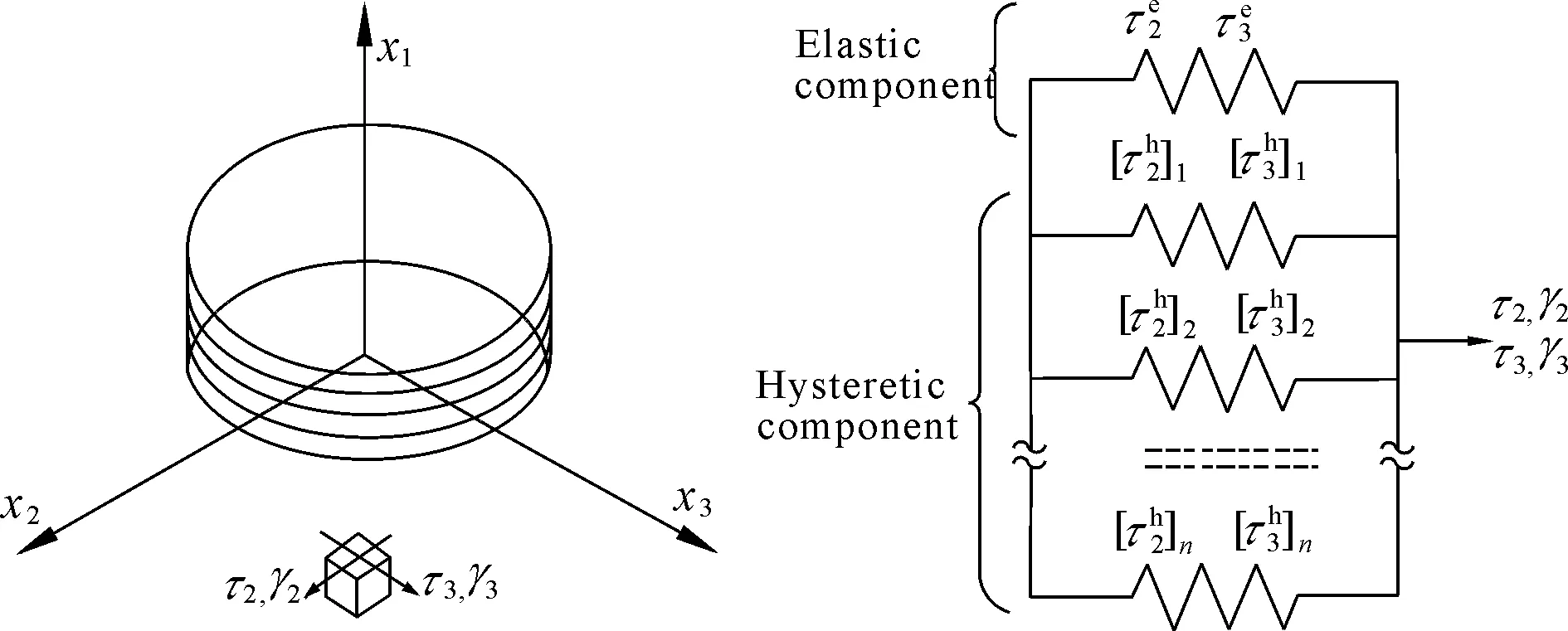
图10 DHI模型示意图

Fujita[30]是最早提出了变形历史积分(deformation history integral，简称DHI)模型，Kato、Mori和Masaki等[31-32]通过实验验证，说明了DHI模型对不同尺寸的高阻尼橡胶支座的适用性。图10展示了高阻尼橡胶支座HDRB的DHI模型概念，它包括一个弹簧单元和几个滞回单元。在该模型中水平方向的弹性分量由下式推出：

(10)

(11)

其中:

(12)

(13)

弹簧单元包括三个参数，分别是附加弹性刚度Ga、损伤函数控制应变γd、损伤函数抗力比θ。第i个滞回分量的剪切应力由下式推导出：

(14)

(15)

滞回单元包括两个参数:滞回控制应变γi、滞回控制应力τi，这些参数可以通过加载试验来确定。DHI模型在各种类型的高阻尼橡胶支座(HDRB)上的应用表明[33]：不论隔震支座的尺寸、刚度、阻尼比和橡胶类型，滞回曲线的分析结果与实验结果吻合良好，利用DHI模型可以更精确地计算结构的动力响应。

5.2 HDRB支座的参数取值

本节使用Bridgestone Corporation[34]的高阻尼橡胶隔震支座，使用的直径800 mm和直径900 mm的HDRB分别代替原来相应的直径，具体参数见表5。Mori等给出了相关的DHI参数推荐值，见表6，而本文参考其DHI参数进行下面的分析。不过值得一提的是两种橡胶材料一样但直径不一样的HDRB支座，它们的DHI参数是相同的，因为它们实际上描述的是支座中橡胶的特性，但是由于尺寸不同，他们的力学性能也不尽相同。

5.3 HDRB和LRB的隔震性能对比

从图5的IDA分析的结果中可以得出，在1158号和1244号地震波下大底盘多塔层间隔震结构的支座位移达到限值，因此本节只在这两条地震波下进行HDRB和LRB的对比，对这使用不同支座的结构分别进行模态分析和中震、大震和极大震下的动力时程分析。

表5 HDRB的物理特性

表6 HDRB的DHI模型参数

(1) 两结构模态对比。从表7中可以看出，HDRB的基本周期要略小于LRB结构，前四阶的基本振型也几乎相同。

表7 HDRB和LRB隔震结构的模态对比

(2) 滞回曲线对比。提取同一位置两结构铅芯橡胶支座(LRB)和高阻尼橡胶支座(HDRB)的滞回曲线进行对比如图11所示。

(3) 能量的对比。图12是两种结构在1158波400 gal下的能量图，图中可以看出HDRB的非线性滞回耗能占比明显大于LRB结构。

图11 1158号地震波下支座的滞回曲线对比

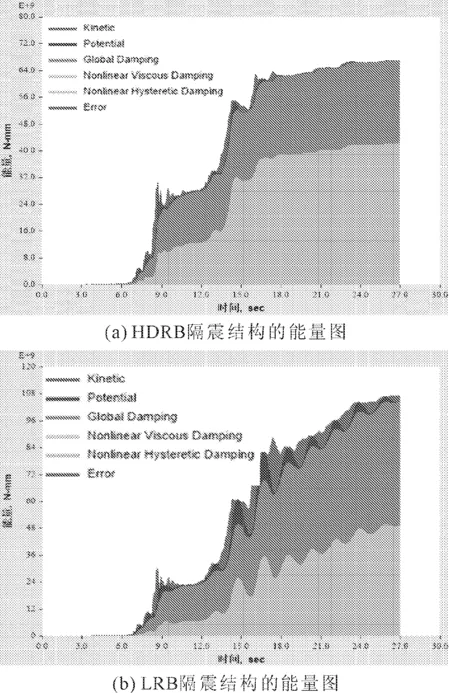
图12 两种结构在1158波400 gal下的能量图

表8是具体的能量数值对比，从表中可以看出，两种隔震结构在相同的地震波下，HDRB结构的输入能量要比LRB隔震结构的输入能量小，HDRB支座的耗能占比随着地震动峰值的增大不变，而LRB隔震结构的支座耗能随地震动峰值增大而减小，从而可以看出HDRB支座在强震下要比LRB支座具有更好的耗能能力。

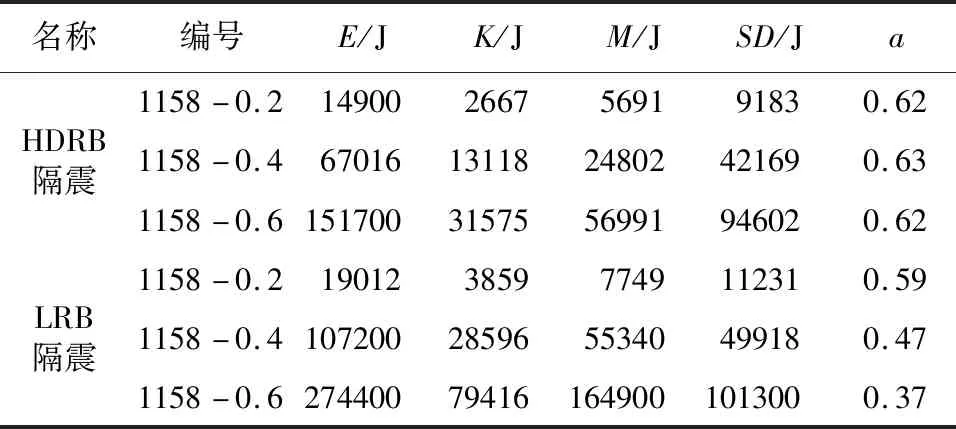
表8 HDRB和LRB结构的能量占比

(4) 层间位移角的对比。位移角的对比情况如图13和图14，从位移角的对比图中可以得出，两种结构大底盘的位移角基本相同，没有明显的区别。塔1和塔3在不同地震波下HDRB结构的位移角曲线和LRB结构的位移角曲线整体趋势相同，但位移角最大值要小于LRB结构，其中在1244号地震波下，HDRB结构塔楼的位移角最大值远小于LRB结构，差值在18%左右。

图13 地震波下不同地震动峰值塔1的X向位移角对比

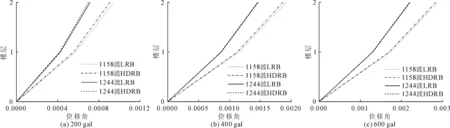
图14 地震波下不同地震动峰值大底盘的X向位移角对比

(5) 基底剪力的对比。大底盘基底剪力时程曲线对比如图15和图16所示，从图中可看出两者的大底盘底部剪力时程曲线近乎吻合，但是HDRB结构的峰值要略小于LRB隔震结构。

图15 1158号波大震下大底盘基底剪力时程曲线对比

图16 1244号波大震下大底盘基底剪力时程曲线对比

(6) 顶层位移的对比。图17与图18所示为两结构顶层位移时程曲线对比图，在1158号地震波作用下，7.5 s之前两结构顶层位移时程曲线近乎吻合，随着时间增大，HDRB结构的顶层位移逐渐小于LRB结构，在1124号地震波下有相同的规律。

图17 1158号地震波大震下顶层位移时程曲线对比

图18 1244号地震波大震下顶层位移时程曲线对比

(7) 楼层加速度的对比。表9和表10为楼层加速度对比，从表中可看出，在1158和1244地震波200 gal下HDRB隔震结构的楼层加速度是要大于LRB结构，而随着地震动峰值增大，楼层加速度逐渐小于LRB结构。

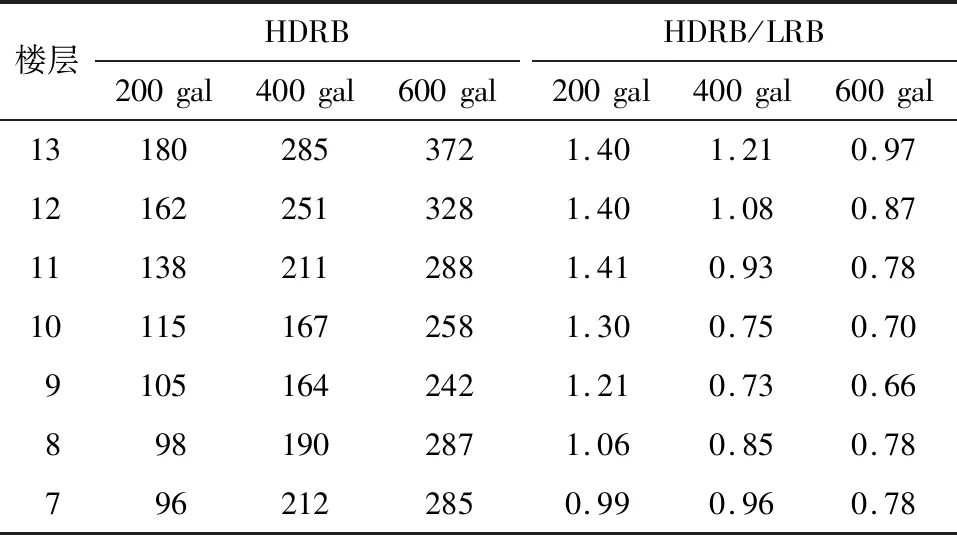
表9 1158号地震波下塔1楼层加速度对比 单位:cm/s2

(8) 楼层扭矩的对比。为了探究两种支座对结构的扭转效应，提取楼层的扭矩进行对比，如图19所示。当地震动峰值为200 gal时，HDRB隔震结构的塔1和塔3楼层扭矩整体是相应的大于LRB隔震结构，然而随着地震动峰值逐渐增大，HDRB隔震结构的扭矩逐渐小于LRB隔震结构。

(9) 隔震层位移的对比。由于隔震结构在最大剪应变作用下的阻尼增大和硬化效应，HDRB会在较大的地震烈度下控制隔震层的位移，图20是两种隔震支座结构在中震、大震、极罕遇地震下LRB结构的隔震层位移和HDRB结构的隔震层位移对比。从图中可以看出，HDRB结构的隔震层位移远小于相同直径的LRB隔震结构的隔震层位移，在1158波下PGA为200 gal时，HDRB隔震结构的位移仅是LRB隔震结构位移的54%，当PGA为400 gal和600 gal时，分别是58%和55%。

5.4 HDRB和LRB结构的抗倒塌性能对比

将HDRB结构的易损性曲线与LRB隔震结构的易损性曲线汇总起来进行对比，如图21所示，发现两者对于下部结构的易损性曲线近乎吻合，而对于支座位移和上部结构在不同地震动作用下HDRB隔震结构的倒塌概率均小于LRB隔震结构。

表10 1244号地震波下塔1楼层加速度对比 单位:cm/s2

图19 不同地震动下塔1的楼层扭矩对比

图20 地震波下LRB和HDRB的支座位移对比

图21 HDRB结构与LRB结构易损性曲线

6 结 论

(1) 当PGA达到0.4g时，支座位移的倒塌概率为2.1%，当PGA达到0.6g时，支座位移倒塌概率为7.49%，上部结构倒塌概率为0.94%，下部结构倒塌概率为1.39%。满足FEMA P695对最大考虑地震(MCE)的倒塌限值10%。从中可以看出，隔震支座位移是决定层间隔震结构抗倒塌能力的关键。

(2) 在罕遇地震和极罕遇地震作用下，大底盘多塔层间隔震结构的倒塌概率分别为4.5%和9%，满足我国《建筑结构抗倒塌设计规范》中规定的可接受倒塌概率。

(3)同样采用直径为800 mm和900 mm的支座，且布置位置相同，两种隔震结构在相同的地震波下，HDRB结构的输入能量要比LRB隔震结构的输入能量小，HDRB支座的耗能占比随着地震动峰值的增大不变，而LRB隔震结构的支座耗能随地震动峰值增大而减小；同时HDRB隔震结构的塔楼位移角最大值小于LRB隔震结构，大底盘一二层的位移角基本相同；从楼层扭矩对比图可看出，当地震动峰值为200 gal时，HDRB隔震结构的塔楼层扭矩整体是相应的大于LRB隔震结构，然而随着地震动峰值逐渐增大，HDRB隔震结构的扭矩逐渐小于LRB隔震结构；最关心的是隔震支座位移，HDRB隔震结构的隔震支座位移远小于LRB隔震结构，仅为LRB隔震结构的54%。