混凝土抗冻耐久性的数值计算研究

潘 素 明

(中铁十八局集团第五工程有限公司，天津 300459 )

我国地处北温带，在冬季北方及南方的一些地区气候都十分寒冷，恶劣的自然环境条件对混凝土的抗冻耐久性提出了更高的要求[1-3]。在我国的三北地区，大部分的建筑物或者构筑物或多或少都受到冻融破坏的影响，混凝土在冻融作用下极易发生剥蚀破坏从而影响力学性能[4-5]，这些地区混凝土的抗冻耐久性必然对混凝土的寿命产生直接影响[6-7]。目前利用现场冻融试验对混凝土冻融损伤进行分析存在诸多不便，众多不可抗力因素的影响会使得试验得到的结果与实际工程应用存在一定的差距[8]。因此，可以利用数值模拟来解释混凝土在冻融循环过程中的破坏机理以及各项力学性能的变化，为提高混凝土抗冻耐久性提供理论支撑。

郭利霞[9]等分析了混凝土的冻融特性，提出了随龄期变化的混凝土力学特性模型，并利用有限元仿真计算程序对混凝土在实际工程中可能产生的冻融破坏的过程进行数值模拟，发现模拟结果与实际冻胀开裂规律一致；李飞等[10]完善并且总结出了混凝土冻融破坏损伤模型，通过室内试验获取了在不同冻融循环次数下混凝土的力学性能变化情况，并且同时运用 ABAQUS有限元软件进行模拟，构建出了大坝混凝土的渗流场以及温度场，不仅找出了坝体发生冻融损坏概率的最高点，而且获得了不同冻融循环次数给坝体稳定性所造成的制约作用；马德群[11]运用ANSYS有限元软件模拟了饱水状态的混凝土在冻融循环状态下的温度场与温度应力，发现在冻融循环状态下混凝土边角点处受到拉应力的最大值超过了抗拉强度设计值从而发生破坏；颉玉龙[12]运用了微焦点工业CT成像技术，通过对不同强度的混凝土微观结构进行扫描并在医学影像处理软件Materialise Mimics中还原，利用有限元软件重建混凝土的微观模型后并对混凝土的冻融循环过程进行模拟，从中发现降低水灰比或者提升含气量都能有效提高混凝土的抗冻耐久性；周禹辛等[13]利用有限元软件ABAQUS，将冻融循环次数和加载速率分别作为变量，通过模拟总结分析了三种不同标号的混凝土受到的应力-应变大小的变化趋势并发现：在冻融循环状态下，混凝土受到的应力-应变的最大值往往随着混凝土强度等级的提高而增大；兰薇等[14]以现场试验为基础，模拟了C30、C40、C50三种型号的混凝土在不同冻融循环次数和水灰比的条件下的应力-应变情况，发现混凝土的劣化程度与受到的应力-应变大小成正比，减小水灰比可以有效缓解冻融循环的破坏作用对于混凝土结构内部的侵蚀；王建伟等[15]利用了ABAQUS有限元软件建立了受冻融混凝土单轴受压本构模型，研究了混凝土经冻融后的动态加载特性并发现：当冻融次数相同时，混凝土的抗压强度随着应变率的增大而增加，峰值应变随之减小。

本文采用ABAQUS有限元软件模拟了标准C50混凝土完整的冻融循环过程，分析了数值模拟过程中温度场、温度应力场以及动弹性模量的变化规律，并与室内试验结果进行了对比，对混凝土的抗冻耐久性做了进一步的研究。

1 室内冻融循环试验

1.1 试验方案

本研究使用的是标准C50混凝土，为了保证力学性能和抗冻耐久性，根据《混凝土外加剂应用技术规范》[16](GB 50119—2013)加入引气剂，掺量为水泥用量的0.01%，配合比设计详情可见表1。

表1 标准C50混凝土配合比设计

本次冻融循环试验采用快速冻融法，试验方案是基于《普通混凝土拌合物性能试验方法标准》[17](GB/T 50080—2002)以及《普通混凝土长期性能和耐久性能试验方法标准》[18](GB/T 50082—2009)而设计的。试验选用6个规格为100 mm×100 mm×400 mm棱柱体试件，编号后进行标准28 d水养，随后开展冻融循环试验。根据现有研究成果[19-20]可知C50混凝土的冻融循环次数约为150次，故设定本次试验冻融循环次数为160次，冻融循环周期设置为4 h，冻融时间间隔不超过10 min，试件每20次冻融循环取出一次，通过对试验前后混凝土试件的外观变化、质量损失率、动弹性模量的变化进行分析，研究混凝土的冻融损伤规律。

1.2 试验结果分析

1.2.1 外表观察

标准C50混凝土从冻融循环开始直到试验结束，混凝土表面的砂浆保持相对完整，不存在大面积的骨料裸露，只有部分试件的边角出现损坏，外观具体变化情况如图1所示。

图1 C50混凝土冻融循环试验前后外观变化情况

1.2.2 动弹性模量

每20次冻融循环后测试试件的动弹性模量，所测得动弹性模量详情如表2所示。

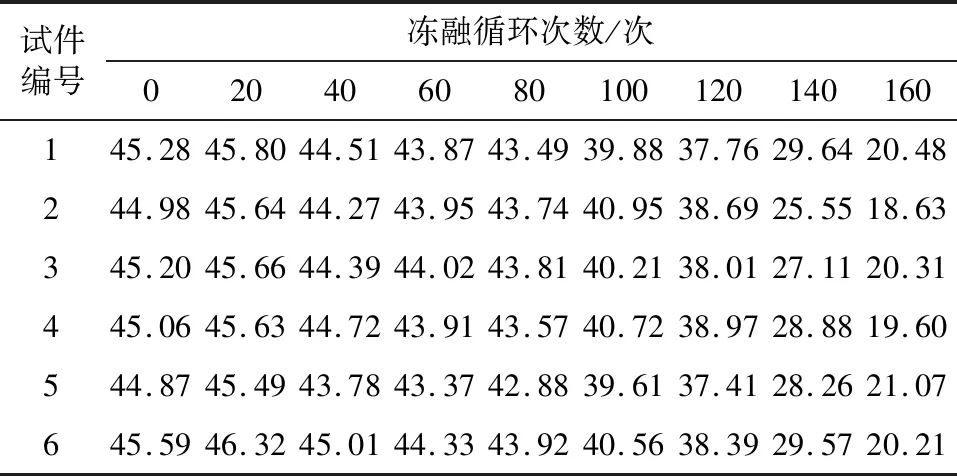
表2 C50混凝土冻融循环下动弹性模量测试结果 单位:GPa

从表2可见，随着冻融循环次数的不断增加，混凝土的动弹性模量呈现出先增后减的变化趋势，当冻融循环达到160次时，各试件的动弹性模量损失率均已明显超过40%，符合试验停止要求[21]。

1.2.3 质量损失率

称得混凝土试件的初始重量平均值为10.014 kg，每20次冻融循环之后测量6块混凝土试件的质量并取平均值，相关测试结果如图2所示。

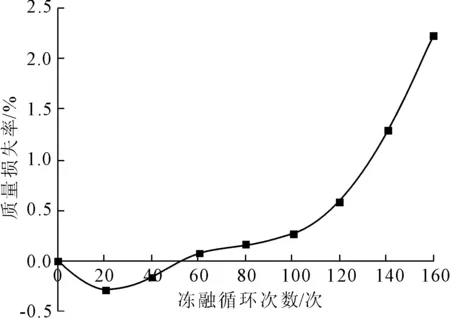
图2 C50混凝土冻融循环质量损失率变化趋势

由图2可见，混凝土试件在冻融循环过程中质量也同样呈先增后减的变化趋势，且在第120次冻融循环后质量损失率开始急速增加，但冻融循环达到160次时，混凝土质量损失率也仅为2.215%，并未超过规范值。

2 有限元模拟及结果分析

2.1 模型建立

为了更好的模拟混凝土冻融循环过程，结合试验特点，选择顺序耦合热应力分析法作为C50混凝土冻融循环的数值模拟方法，建立规格与室内试验相同的100 mm×100 mm×400 mm的混凝土长方体构件模型，网格划分采用DC3D8八节点线性传热六面体单元，格间距离设置10 mm，单元类型设置为Heat Transfer类型。网格划分完成后，为了后期更加直观观察混凝土内外部的温度场的变化情况，故在模型的内部和表面分别选取输出点：A、C点分别取在长方体100 mm×100 mm底面的左上顶点和中点，B点则取为底面100 mm边上的中点；内部E点取为长方体模型的重心处，D点为C、E两点连线的中点，具体布置见图3。

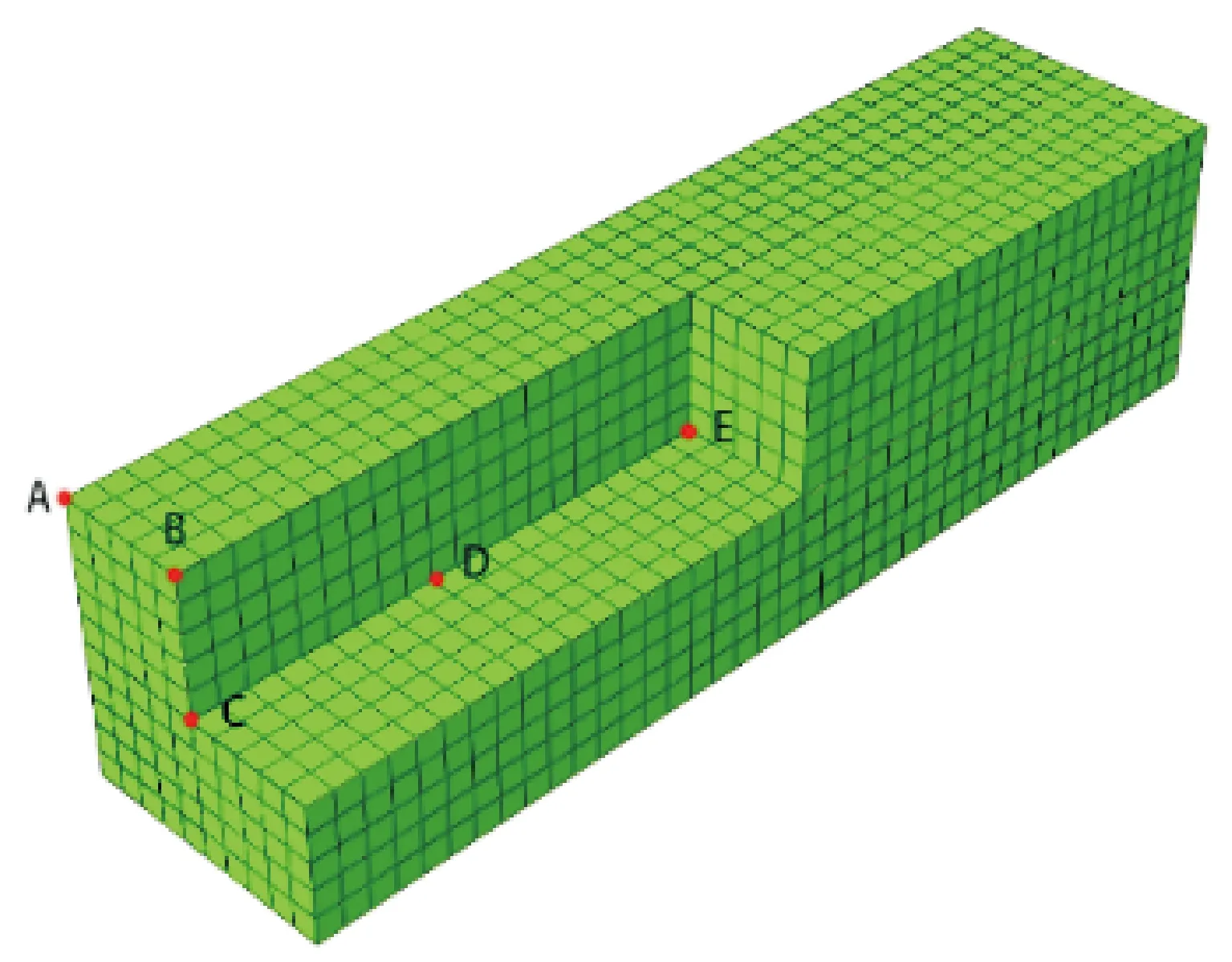
图3 网格划分与输出点选取

(1) 导入热力学参数，具体数据如表3所示。

表3 材料热力学参数

(2)为了与室内冻融循环试验更加契合，模拟设定每个冻融循环为4 h，温度从20℃到-20℃到20℃，温度变化趋势如图4所示，冻融循环次数为160次，共计640 h，即2.304×106s。设置在冻融次数为20、40、60、80、100、120、140、160次，即2.88×105s、5.76×105s、8.64×105s、1.152×106s、1.44×106s、1.728×106s、2.016×106s、2.304×106s时输出结果。

(3) 分析步类型设置为热传递，荷载方式为瞬态，分析总时长为2.304×106s，并设置每2.88×105s即每20次冻融循环输出一次结果。分析步步长设置越小，计算结果越准确，因此设置为9.6×102s，即每20 min进行一次运算。同时，还需要通过设置幅值来模拟冻融循环作用，创建幅值类型选为Tabular(表格型幅值曲线)，时间跨度设置为分析步时间。

(4) 在分析步设置完成后，由于研究采用瞬态热分析作为冻融循环状态下的数值模拟分析方法，故边界条件选定类型为温度类型，选择混凝土模型整体作为施加区域。

图4 每个冻融循环内温度的变化规律

2.2 温度场模拟分析

在有限元软件ABAQUS中，将混凝土构件模型进行160次冻融循环，每小时得到1次温度云图。以第一次冻融循环为例，输出的温度云图如图5所示。

将图5中0 h～4 h内各个输出点的温度统计得到图6。

由图5、图6可见：

(1) A、B、C、D、E点在每一个冻融循环内的温度变化规律都与温度场变化保持一致，且各输出点在0 h～4 h内所形成的温度变化曲线也与试验所用快速冻融机在一个冻融循环内所反映的温度变化趋势一致，都呈现出余弦函数的变化规律。

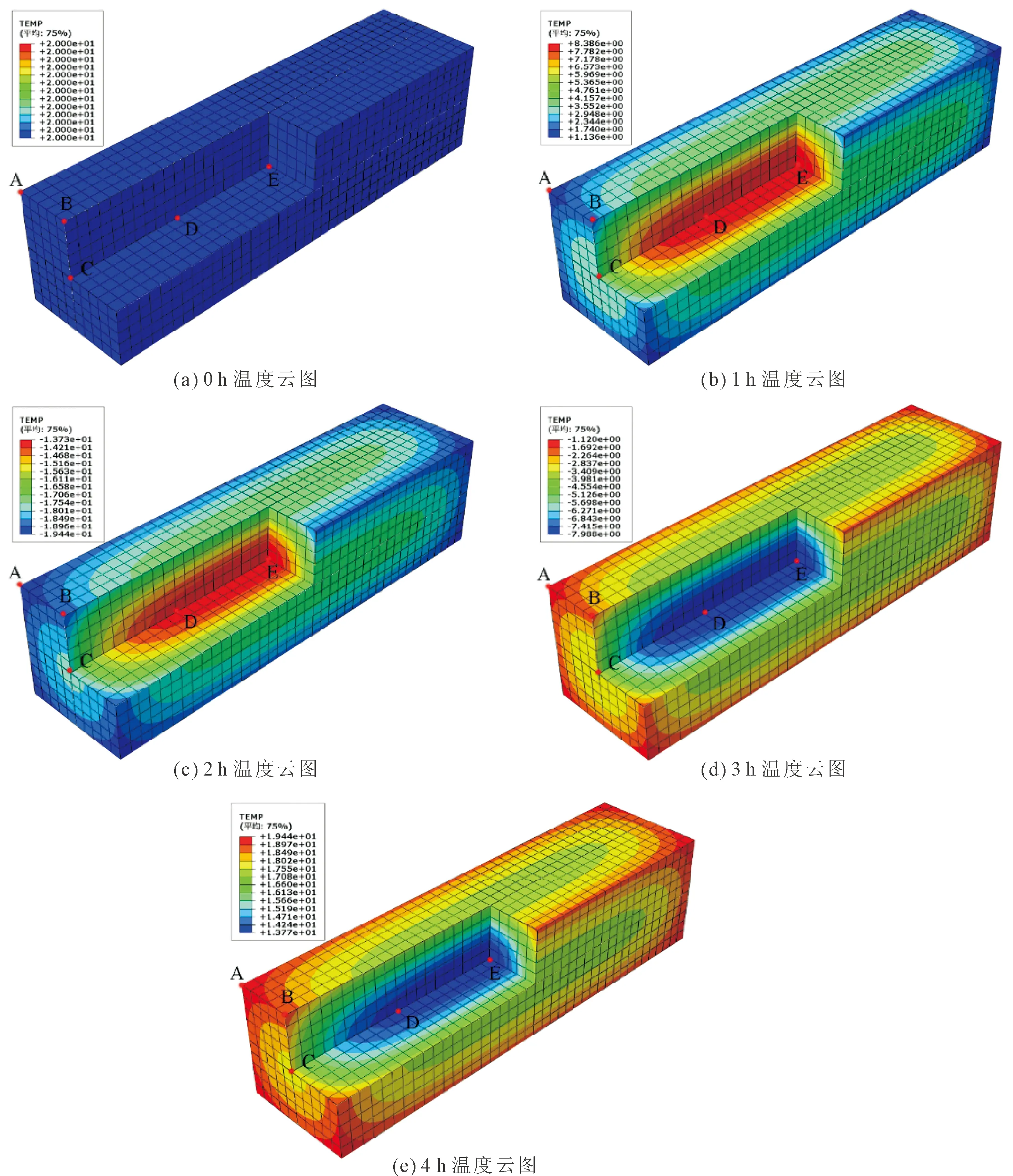
图5 0 h～4 h混凝土模型温度云图

(2) 混凝土模型表面的输出点A、B、C三点的温度变化幅值明显大于混凝土内部输出点D、E两点，各个输出点的温度都在-20℃～20℃之间变化，但均未超过预设幅值，这与试验实际情况也吻合。混凝土热量的传递是一个时效性的过程，从混凝土表面传递到其内部中心点存在一定的时间间隔，且在热传导过程中能量会不断损耗，故传递到中心点时的热量要远小于表层。

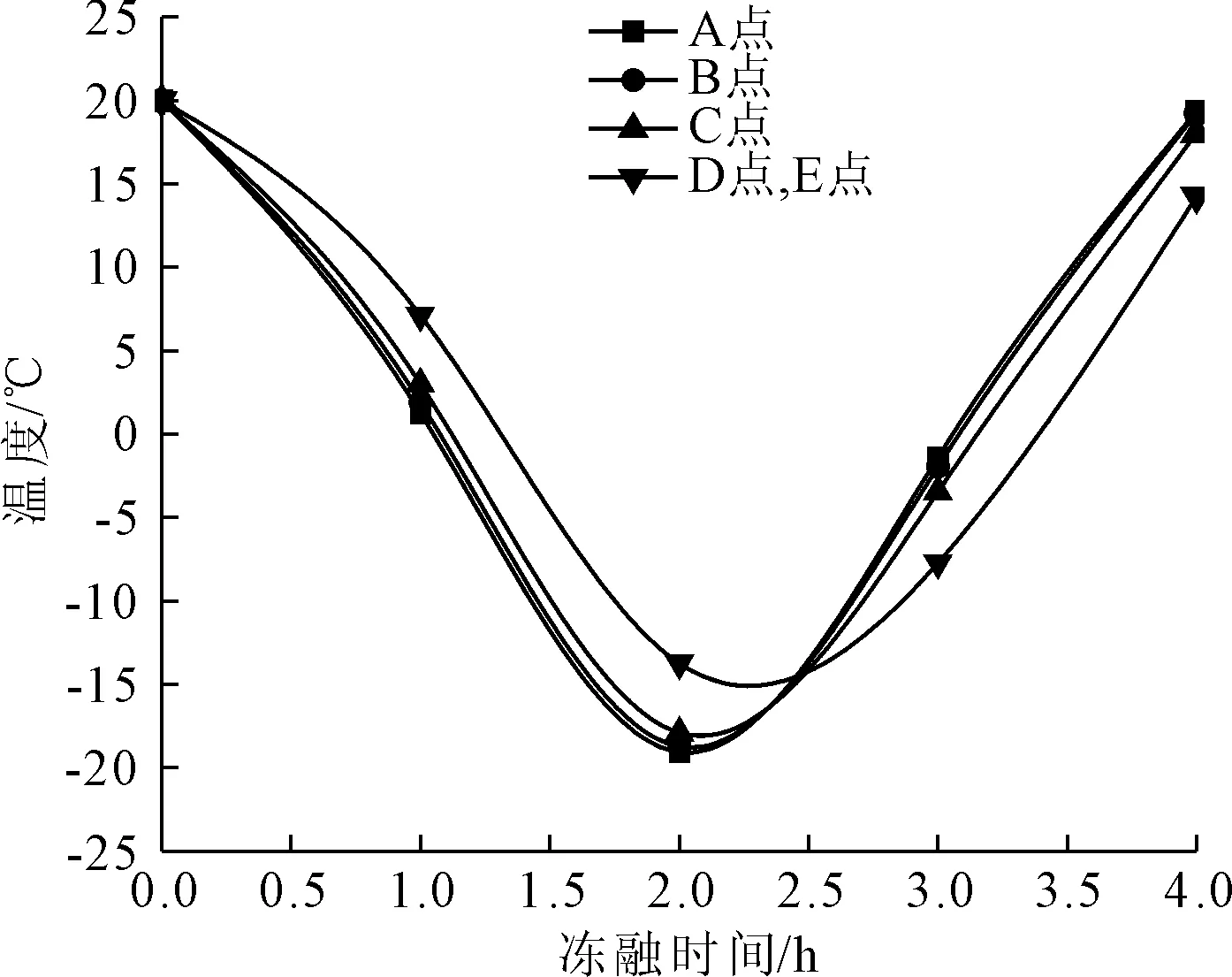
图6 0 h～4 h冻融循环各输出点温度变化趋势

2.3 温度应力模拟分析

将C50混凝土0～160次冻融循环过程中各输出点的温度应力峰值统计分析后得到图7。

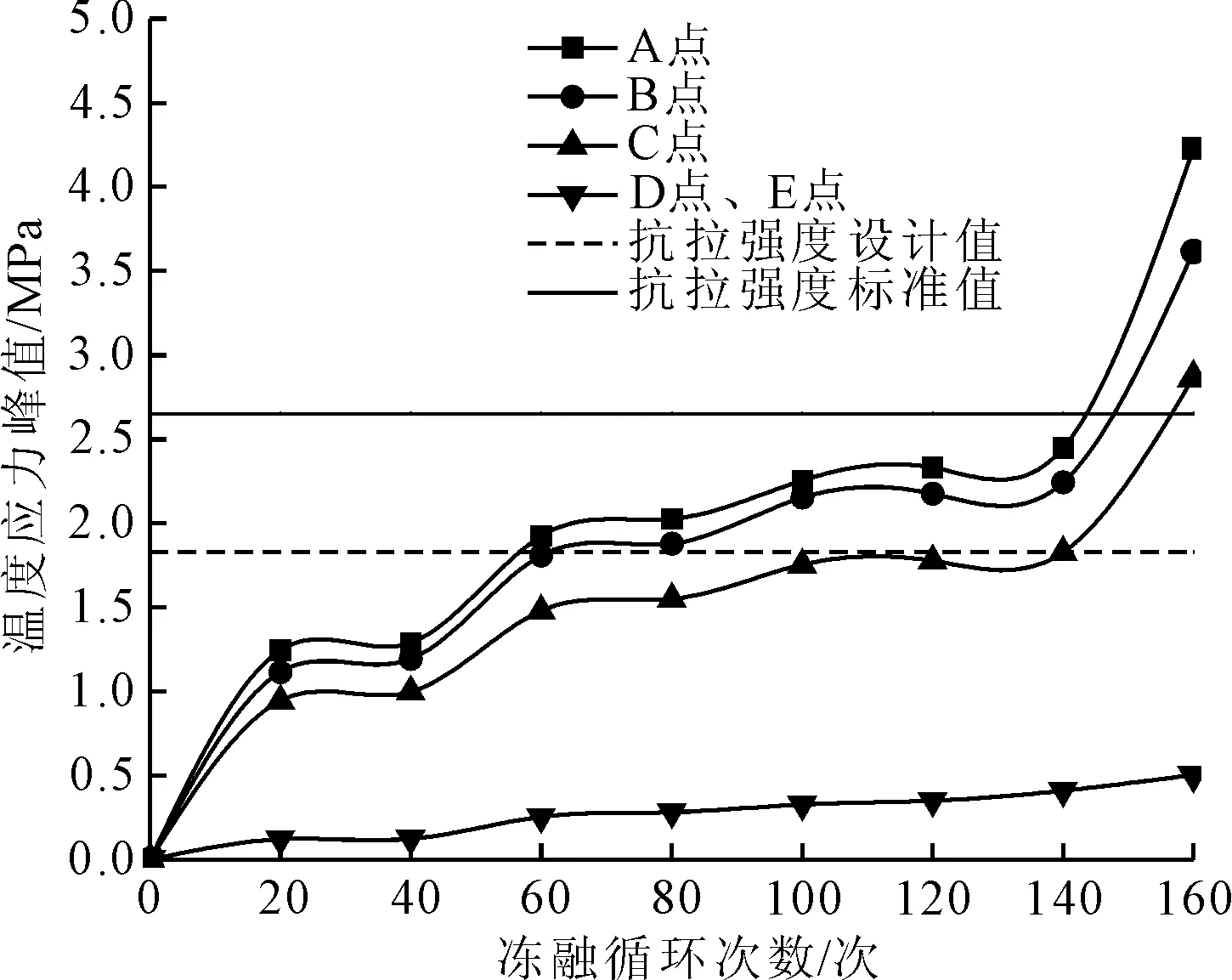
图7 0～160次冻融循环温度应力峰值变化趋势

由图7可以得出：

(1) 随着冻融循环次数的增加，各个输出点的温度应力峰值都呈现出不断增长的趋势。第0次～40次和第60次～120次之间温度应力峰值的增长较为缓慢；第40次～60次时增长速度较快，特别在第140次～160次时呈现出快速上升趋势，且A、B、C三点的温度应力峰值的变化相较于D、E点更明显。

(2)当冻融循环达到160次时，输出点A、B、C、D、E所承受温度应力峰值均达到最大值。根据相关规范[22]得知此时混凝土表面输出点A、B、C点的温度应力峰值均已超过抗拉强度标准值；而混凝土内部输出点D、E点的温度应力峰值并未超过抗拉强度标准值。可见此时A、B、C点发生破坏，故可认为混凝土试件在第160次冻融过程中发生破坏。

2.4 动弹性模量分析

将表3中的混凝土构件模型进行复制，由热分析转换为静力分析，重新定义材料参数，具体数据可参照表4。

由热分析转换为静力分析需重新定义网格类型，将复制的模型重新划分网格，改为采用C3D8R八结点线性六面体单元来划分网格，网格间距为10 mm，与热学分析中网格划分间距保持一致。

将2.2节中温度场的模拟结果导入预定义场作为模型的初始条件，分析步分析方式改为静力、通用分析模式。

表4 材料力学参数

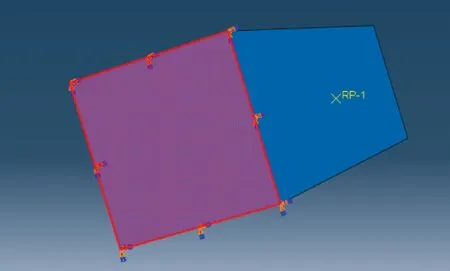
图8 固定底面

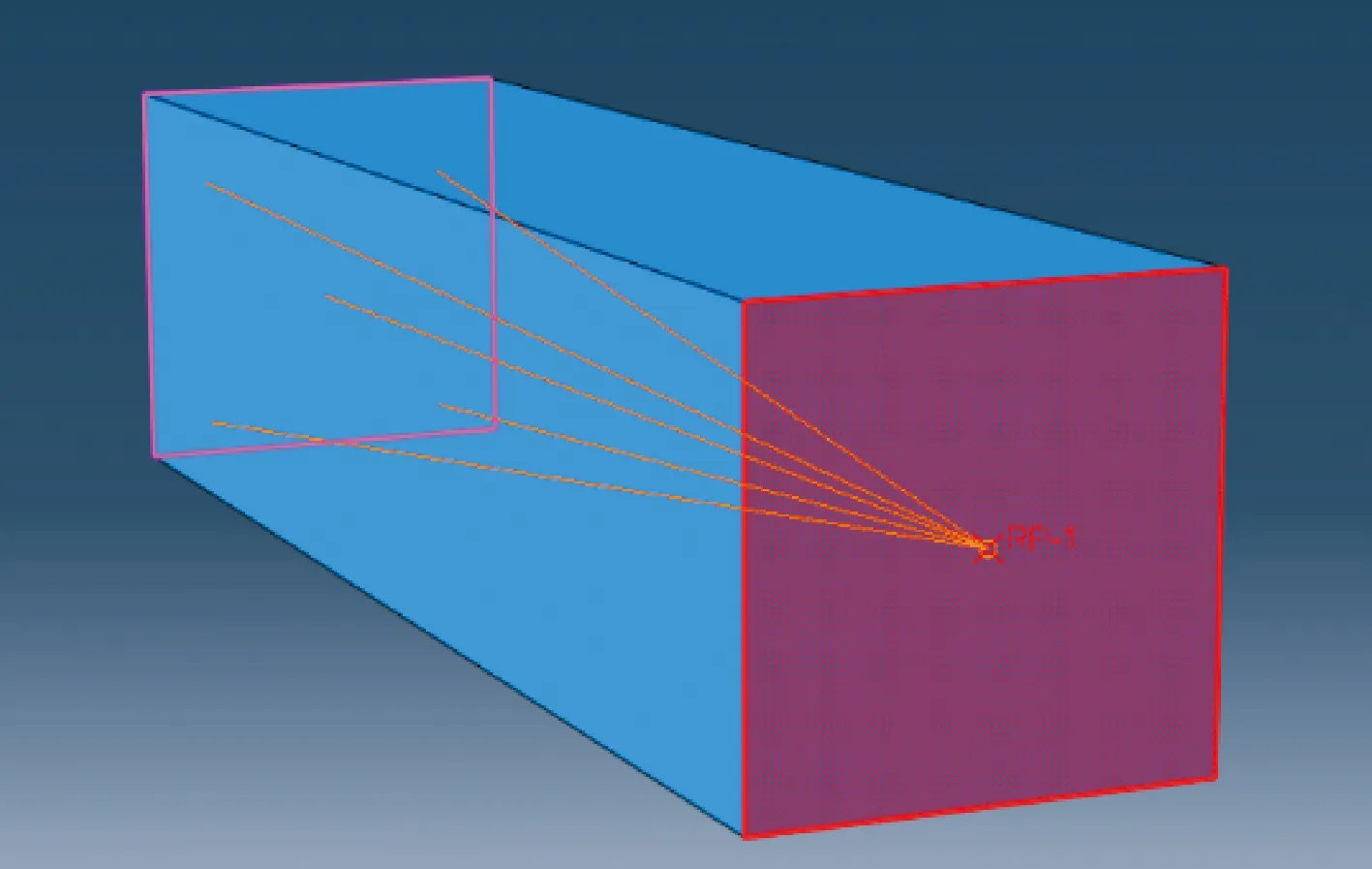
图9 底面耦合

(1)

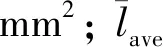
将表2中室内冻融循环试验中所测定的6个混凝土试件的动弹性模量取平均值作为试验值并和通过数值模拟得到的模拟值进行汇总并分别进行计算得出相应的动弹性模量损失率，详情见图10。

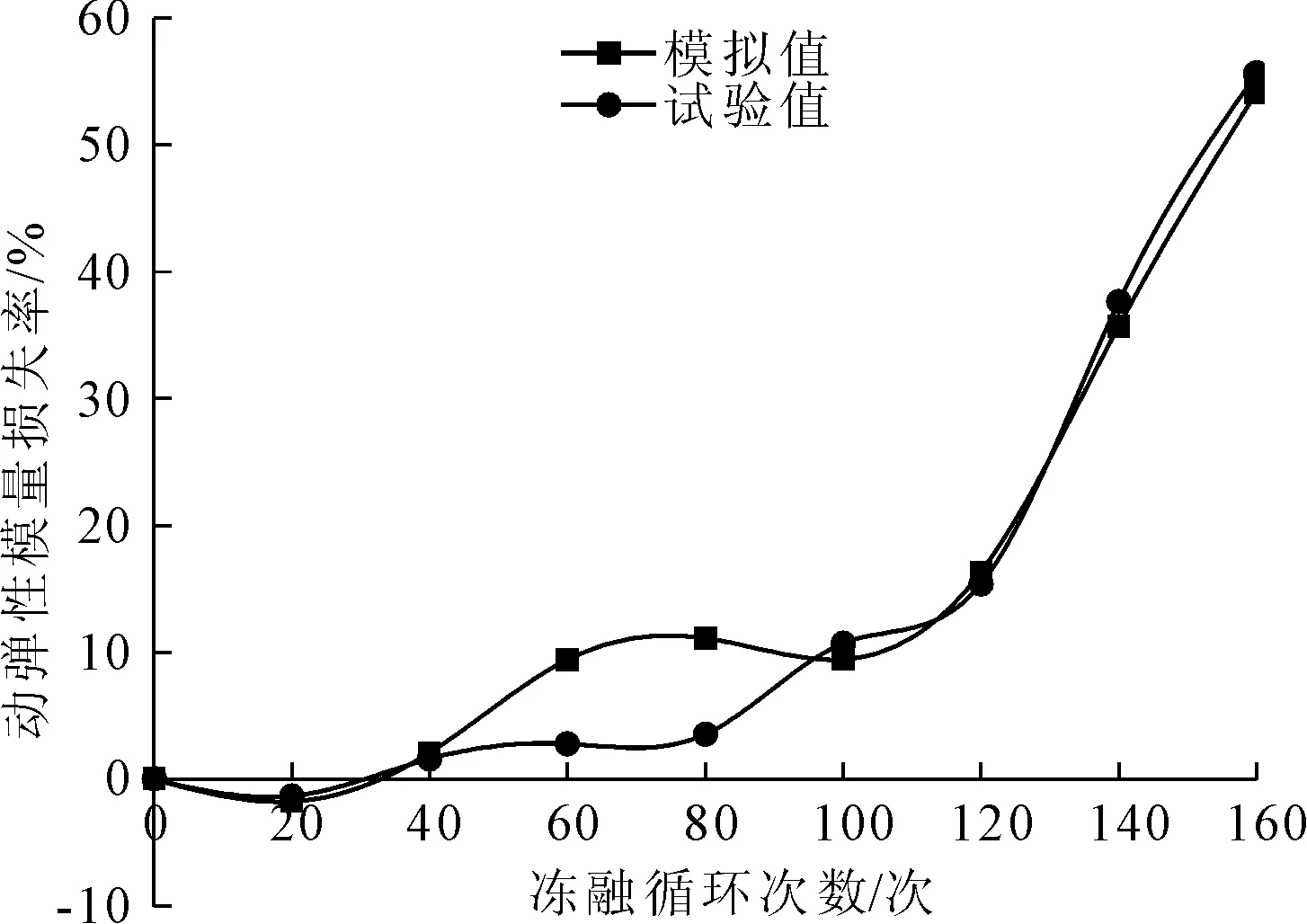
图10 0～160次冻融循环试件动弹性模量损失率变化趋势

从图10可以看出：

(1) 试验测试和数值模拟所得到的动弹性模量的误差较小，二者计算出的动弹性模量损失率的变化趋势都基本一致。在第20次～100次冻融循环过程中，动弹性模量的损失率变化较为缓慢，混凝土外观的破坏程度较为轻微；而在第100次～160次冻融循环过程中，动弹性模量损失率增长变化速度越来越快，冻融循环作用对于混凝土结构内部的侵蚀作用已经越来越深入，混凝土外观的破坏程度愈发严重。

(2) 当冻融循环进行到第160次时，室内实验和数值模拟的动弹性模量损失率分别达到了55.60%和54.16%，均达到了试验停止要求，此时混凝土已经发生破坏，很好的说明了数值模拟结果与室内冻融循环试验结果的一致性。

3 结 论

本文以室内试验为基础，利用ABAQUS有限元软件模拟了C50混凝土的冻融循环过程，对其温度场、温度应力场以及动弹性模量损失率的变化规律进行了总结和分析，具体成果如下：

(1) 在室内冻融循环试验中，当冻融循环进行到160次时，混凝土表面剥蚀现象并不严重，质量损失率虽未超过5%，但动弹性模量损失率均超过40%，试验结束。

(2) 数值模拟中混凝土试件各输出点温度虽未达到预设幅值，但温度变化趋势与预设模拟温度场相同；温度应力的模拟中，当冻融循环次数达到160次时，混凝土表面输出点A、B、C的温度应力峰值均超过了抗拉强度标准值，而内部输出点D、E点温度应力峰值未超过抗拉强度标准值，可认为此时混凝土已经发生破坏。

(3) 动弹性模量的试验值和数值模拟值误差较小，且动弹性模量损失率的变化趋势也基本一致。当冻融循环进行到160次时，二者所得出的动弹性模量损失率分别达到了55.60%和54.16%，均已满足试验停止标准。