中厚板多层多道焊接焊道尺寸与工艺参数相关性研究*

王 强，沈 涛，郭 超

(宜宾职业技术学院，四川 宜宾 644003)

0 引言

中厚板焊接在重型机械、交通运输、船舶工程等领域有着十分广泛的应用[1]，但因焊接工艺的复杂性、焊接件的大型化和环境因素的多变性，导致中厚板焊接生产效率低、焊接质量难以保证。随着人工智能的发展，运用工业机器人焊接替代传统焊接作业已成为解决该问题的有效途径。

在工业机器人焊接中，焊接路径规划是首要问题，而焊接工艺成型参数规划又是焊接路径规划的重要基础[2，3]。因此，本文以CO2气体保护焊为基础，通过熔敷焊接试验，重点研究分析了中厚板焊道尺寸与成型工艺参数之间的相关性，并建立起相应的方程模型，为焊接路径规划选择合理工艺参数提供数据参考。

1 试验方案设计

考虑到中厚板焊接过程中的影响因素较多，为减少试验次数，更好地获得旋转性和便于直接寻找最优区域，本次试验采用旋转回归设计方法，以CO2气体保护焊为基础进行熔敷焊接试验。旋转回归设计方法的组合设计参数如表1所示。其中，p为因子变量数，即工艺参数数目；mc为全面试验点数；r为星号臂长度；m0为重复试验次数；n为总试验次数。

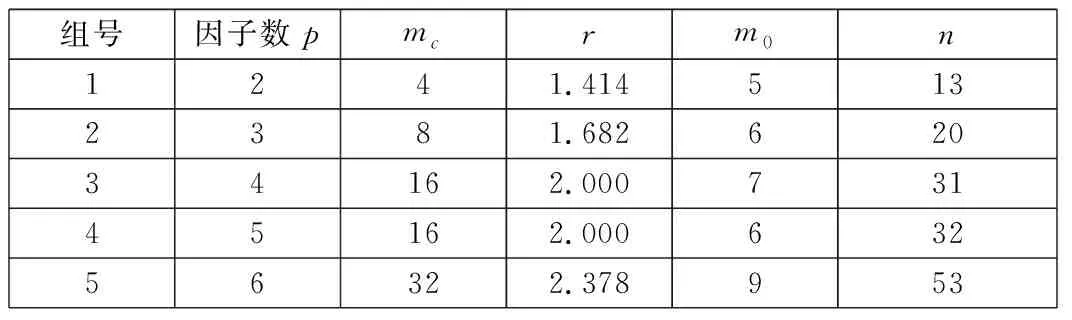
表1 组合设计参数

本试验采用FANUC焊接机器人Pulse MIG-500RP,焊接试件材料为Q345,尺寸为200 mm×60 mm×20 mm，焊丝采用直径为1.2 mm的ER50-6。考虑到喷嘴高度和焊接电压对CO2气体保护焊的熔敷焊道尺寸影响有限[4]，故本试验主要将焊接电流I和焊接速度v作为因子变量，即p=2，根据组合设计参数可计算得到本试验的参数，如表2所示。

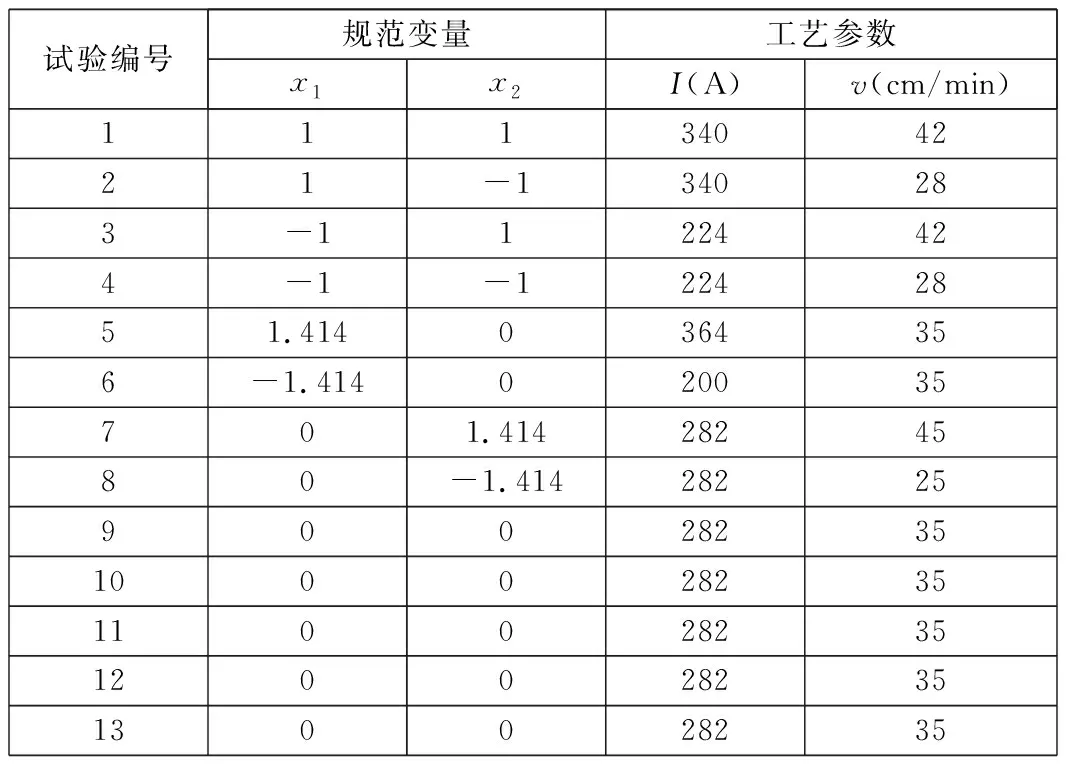
表2 试验参数

2 试验结果获取

首先取试样中段，沿焊缝横截面切割，经抛光打磨去除氧化层及毛边，用高清相机拍摄焊道横截面，便可得到一组焊缝横截面外形照片。然后再利用Image-Pro Plus软件对焊缝横截面外形照片进行标定和数据处理，可获得选择不同焊接工艺参数时的焊缝成型参数。最后算出测试结果的平均值，即可作为本次试验的最终熔覆焊缝成型参数，如表3所示。

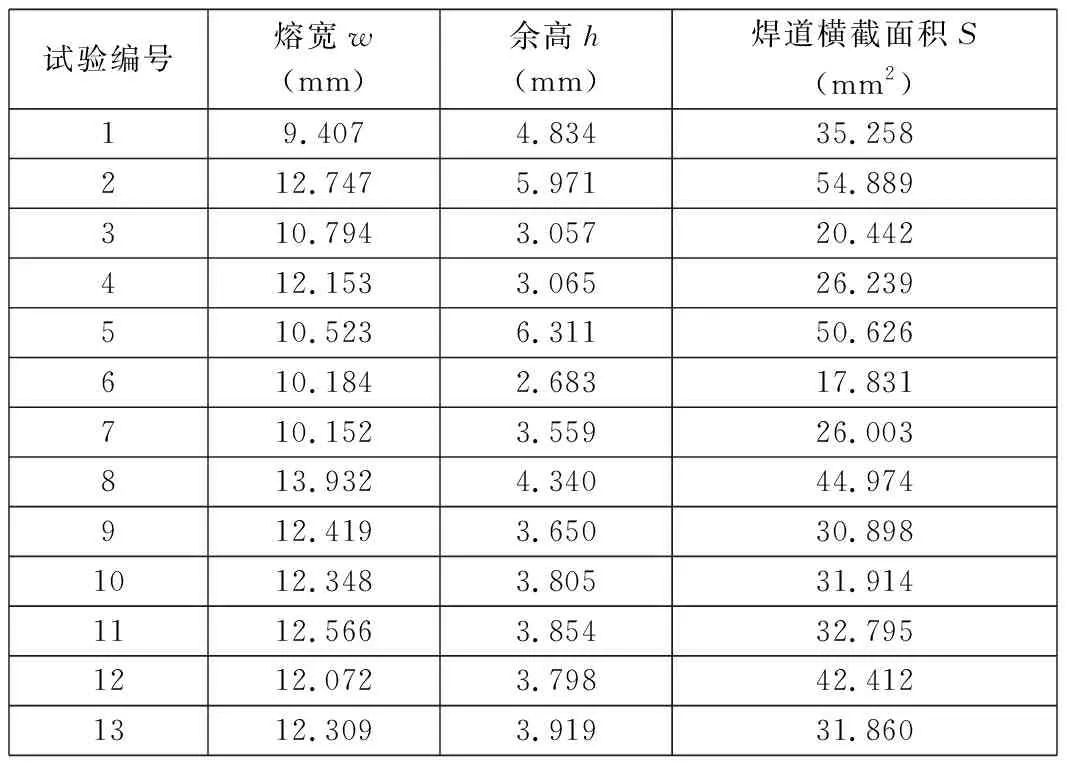
表3 焊道成型参数

3 试验回归分析

通过对上述测试数据的整理分析，建立二次回归数据结构表达式，再根据显著性和拟合性检测结果，修正优化参数后得到熔宽、余高和焊道横截面积的回归方程，最后利用反编码计算获得通用旋转回归方程。

3.1 建立回归表达式

在本试验中，我们仅把焊接电流和焊接速度作为因子变量，因此本试验属于二因数试验，则可把回归数据结构表达式简化为：

(1)

其中：b0、b1、b2、b12、b11、b22为回归系数；x1、x2、x12、x11、x22为自变量的值。

以熔宽为例，在二次通用旋转组合设计计算参数表[5]中选取相应参数，经过计算得到回归系数，从而建立起熔宽的回归方程：

(2)

余高和焊缝横截面积的回归系数计算与熔宽的计算过程相似。

3.2 方程的回归检测

方程的回归检测是指拟合效果和可信程度的检测，主要包括方程的显著性检测、方程的拟合性检测和回归系数的显著性检测三个方面。依据F检测方法的原理，结合试验数据和参考试验优化设计与分析中的临界检测表，经过分析计算可得到回归方程和回归系数的检测数据，如表4和表5所示。

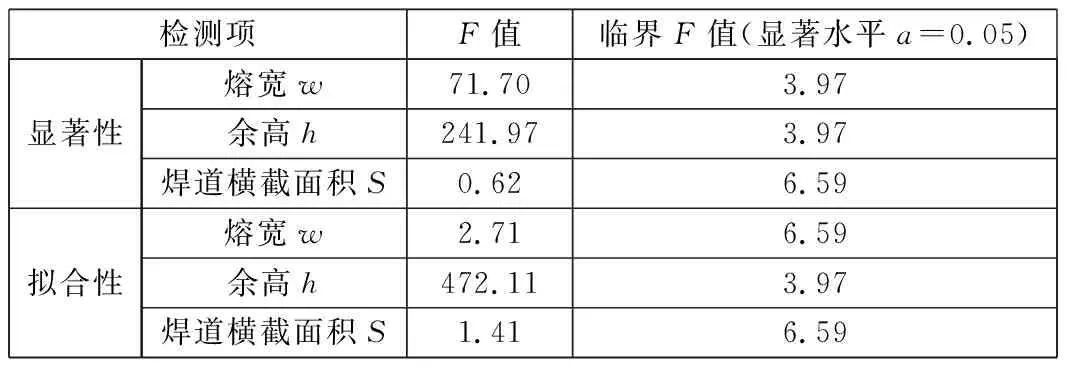
表4 回归方程检测数据

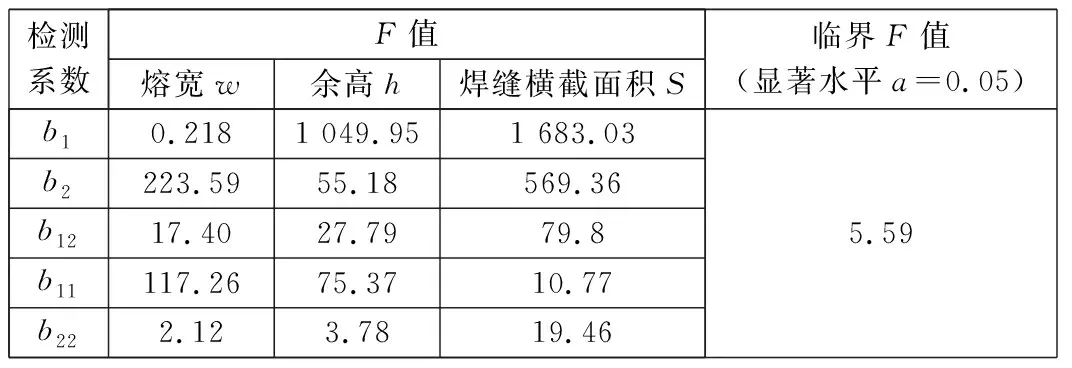
表5 回归系数检测数据

通过分析表4和表5，可以发现：

(1) 在a=0.05水平下，回归方程的显著性和拟合性均符合预期。

(2) 在a=0.05水平下，在熔宽回归方程中,系数b1和b22属于不显著项；在余高回归方程中，系数b22也属于不显著项，均应剔除。

3.3 方程的反编码

经过上述回归检测，剔除不显著项参数后，再经过回归系数的二次计算便可得到新的回归方程。但为了方便直接使用，我们还应对方程进行反编码计算，即将因子变量换算成编码前的实际变量。根据本试验的编码转换原则，其转换表达式如下：

(3)

(4)

将转换表达式代入剔除不显著项后的回归方程中，即可得到焊接工艺参数与焊接成型参数的关系方程如下：

w=-16.160 64+0.203 34I+0.164 62v-
0.001 22Iv-0.000 29I2.

(5)

h=0.520 87-0.011 88I+0.155 85v-
0.000 7Iv+0.000 1I2.

(6)

S=-11.459 61+0.330 23I-0.807 39v-
0.008 52Iv+0.000 29I2+0.032 52v2.

(7)

4 焊接参数与成型参数关系曲线图

利用本试验所建立的方程模型，可以绘制出焊接工艺参数与焊道成型参数的关系曲线图和等高线图，如图1～图5所示。这些图可以更加直观地反映和描述出各参数之间存在的相关性，同时还可以在已知焊道尺寸参数的前提下，借助关系图直接获取工艺参数，为焊道路径规划提供了更便捷的数据来源。

图1 焊接电流I与焊道横截面积S的关系曲线 图2 焊接速度v与焊道横截面积S的关系曲线 图3 熔宽等高线

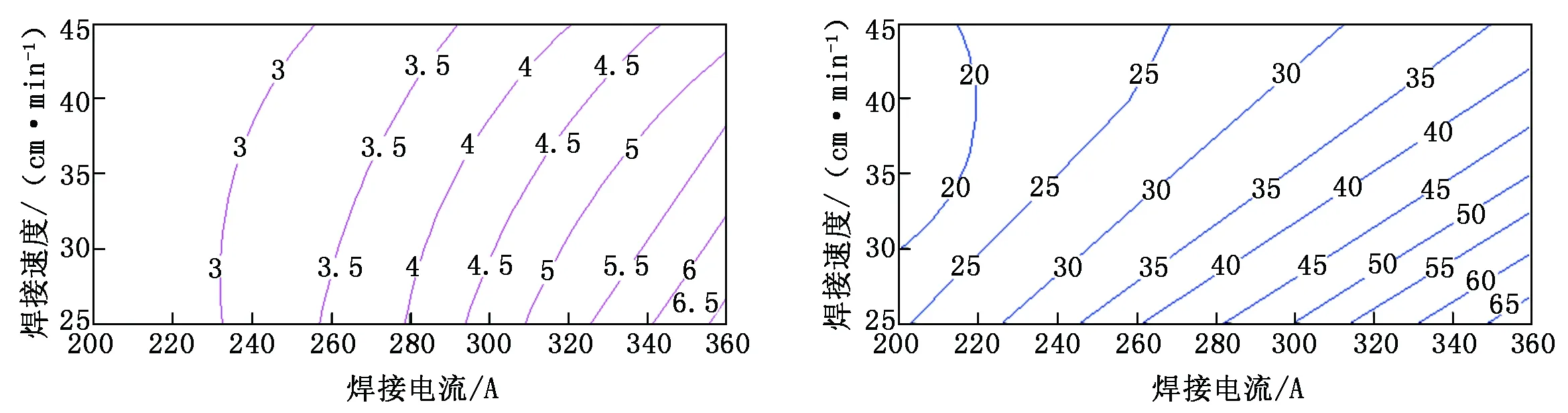
图4 余高等高线 图5 横截面积等高线

5 结论

本文依据旋转回归设计方法的原理设计了本试验，并进行了相关性分析，经过一系列技术处理后获得了焊接成型试验数据，建立起了回归方程模型。然后通过回归检测优化了方程参数，并经过反编码计算获得了焊接参数关系表达式。最后根据表达式绘制了焊接工艺参数与焊道成型参数的关系曲线图，为中厚板机器人多层多道焊接焊道路径规划提供了数据参考。